An ellipse is the set of all points in a plane such that the sum of the distances from two fixed points, called foci, is constant. It has two axes of symmetry, called the major axis and the minor axis. It is a closed and symmetric curve with numerous applications in physics and geometry.
Table of Contents
- How to find the standard equation of an ellipse
- Ellipse with Semi-Major Axis on the y-axis
- How to Find the Equation of a Translated Ellipse
- Relationship between ellipse parameters
- Eccentricity of an Ellipse: Definition, Geometric Meaning and Formula
- Solved Exercises
Let us denote the two foci as \( F_1(-c, 0) \) and \( F_2(c, 0) \), and let \( P(x, y) \) be any point belonging to the ellipse. Then the following relation holds:
\[ |PF_1| + |PF_2| = 2a \]
The constant \( 2a \) – which represents the sum of distances \( |PF_1|\) and \(|PF_2|\) – is always greater than the distance between the two foci, \( 2c \). This concept is illustrated in the following figure:
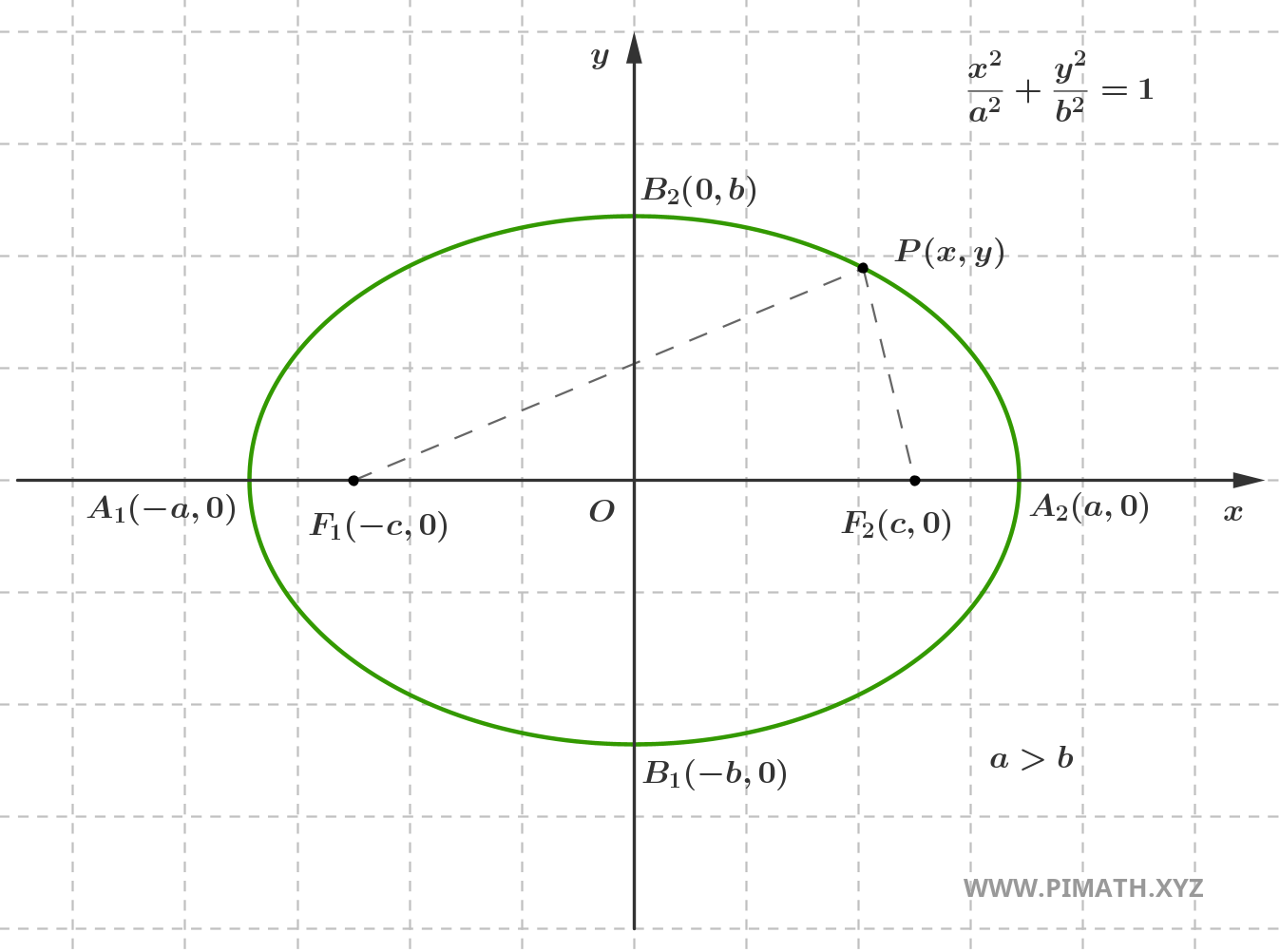
In the image, the segment connecting the center \( O \) to point \( A_2 \) on the horizontal axis is called the semi-major axis, and its length is exactly \( a \). The vertical segment connecting the center to point \( B_2 \) is called the semi-minor axis and has length \( b \).
The relation that defines the ellipse must naturally hold for all points on the ellipse. Let us consider the particular case where point \( P(x,y) \) coincides with point \( B_2(0,b) \):
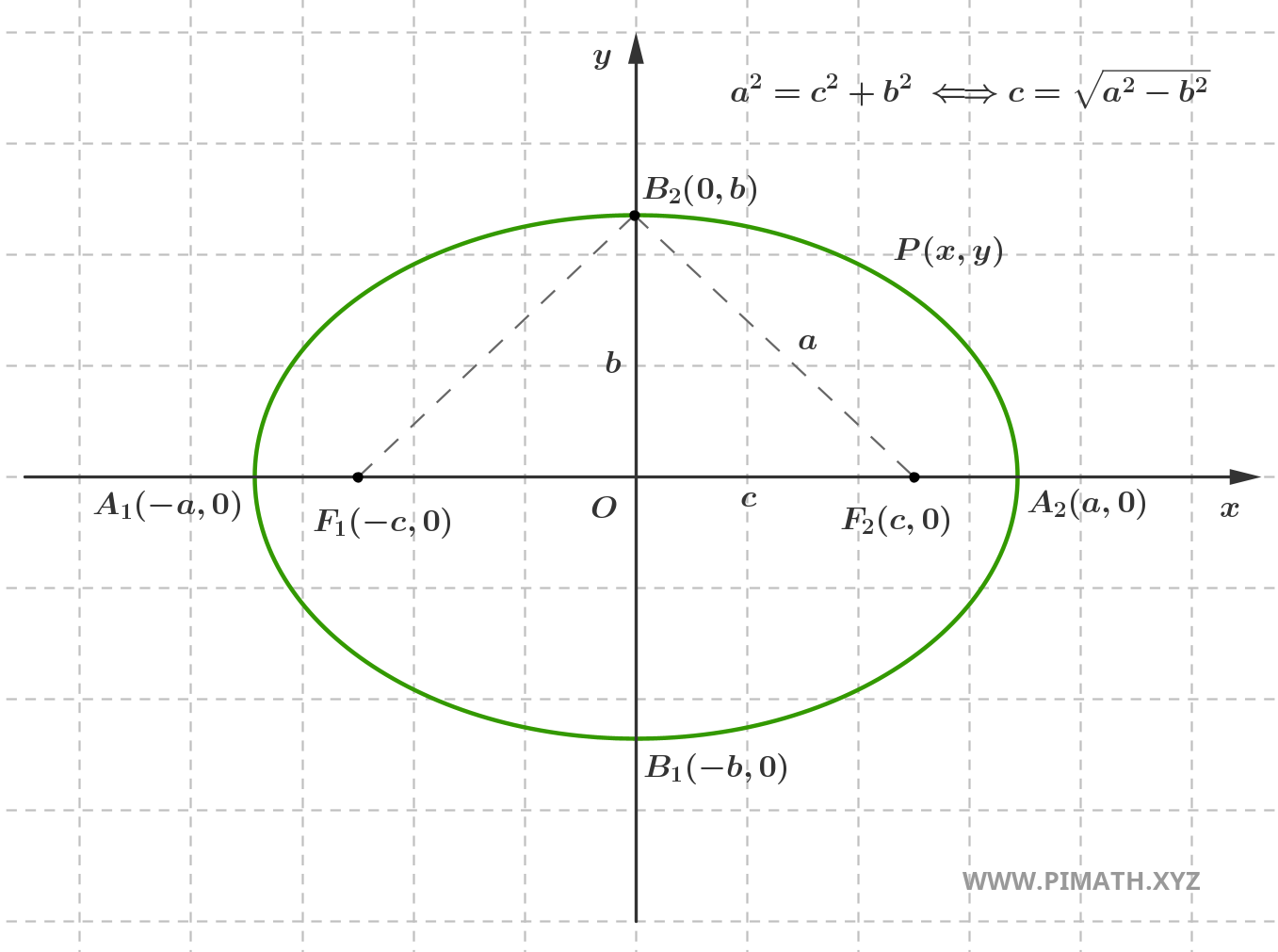
Considering the right triangle with vertices \( O(0,0) \), \( F_2(c,0) \) and \( B_2(0,b) \) and applying the Pythagorean Theorem, we derive that \( c=\sqrt{a^2-b^2} \), as shown in the figure.
How to find the standard equation of an ellipse
Let us consider a simplified case where the center of the ellipse coincides with the origin of the coordinate system, with the foci positioned along the horizontal axis at points \( F_1(-c, 0) \) and \( F_2(c, 0) \).
Consider a generic point \( P(x, y) \) in the plane. For \( P \) to belong to the ellipse, the following relation must hold:
\[ |PF_1| + |PF_2| = 2a \quad , \quad a > c \]
Now we calculate the distances between point \( P(x, y) \) and each of the two foci:
\[ |PF_1| = \sqrt{(x + c)^2 + y^2} \quad \text{and} \quad |PF_2| = \sqrt{(x - c)^2 + y^2} \]
Substituting these expressions into the initial condition we obtain:
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \]
To eliminate one of the radicals, we move \( \sqrt{(x + c)^2 + y^2} \) to the right-hand side:
\[ \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2} \]
We square both sides to eliminate the radical:
\[ (x - c)^2 + y^2 = \left(2a - \sqrt{(x + c)^2 + y^2} \right)^2 \]
We expand the square of the right-hand side:
\[ (x - c)^2 + y^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
We eliminate the \( y^2 \) term present on both sides and expand the squares:
\[ x^2 - 2cx + c^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 \]
Simplifying both sides:
\[ -4cx = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} \]
We divide both sides by 4:
\[ -cx = a^2 - a\sqrt{(x + c)^2 + y^2} \]
We move all terms with the radical to the left-hand side:
\[ a\sqrt{(x + c)^2 + y^2} = a^2 + cx \]
We square both sides again:
\[ a^2[(x + c)^2 + y^2] = (a^2 + cx)^2 \]
We expand both sides:
\[ a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2 \]
Expanding completely:
\[ a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2 \]
We simplify the common terms from both sides:
\[ a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2 \]
We collect like terms:
\[ x^2(a^2 - c^2) + a^2y^2 = a^2(a^2 - c^2) \]
Since \( a > c \), the quantity \( a^2 - c^2 \) is positive. Let us denote it as \( b^2 \), so we obtain:
\[ b^2 = a^2 - c^2 \]
Substituting, we get:
\[ x^2b^2 + a^2y^2 = a^2b^2 \]
We divide both sides by \( a^2b^2 \) to isolate the terms:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , \quad a > b \]
This is the standard form of the ellipse equation with center at the origin and foci on the x-axis. The equation is symmetric with respect to both coordinate axes and with respect to the origin.
Let us introduce some terminology. The line containing the foci is called the focal axis, while the intersection point of the axes is the center of the ellipse.
- The points where the ellipse intersects the focal axis and the line perpendicular to it passing through the center are called vertices of the ellipse.
- The segment \( A_1A_2 \) is called the major axis, while the segment \( B_1B_2 \) is called the minor axis.
- The length \( a \) is defined as the semi-major axis, and the length \( b \) as the semi-minor axis.
Ellipse with Semi-Major Axis on the y-axis
If we want to describe an ellipse that has a vertical semi-major axis, that is, oriented along the y-axis, we simply need to swap the roles of \( a \) and \( b \) in the standard equation that describes the ellipse with semi-major axis on the x-axis, as shown in the figure:
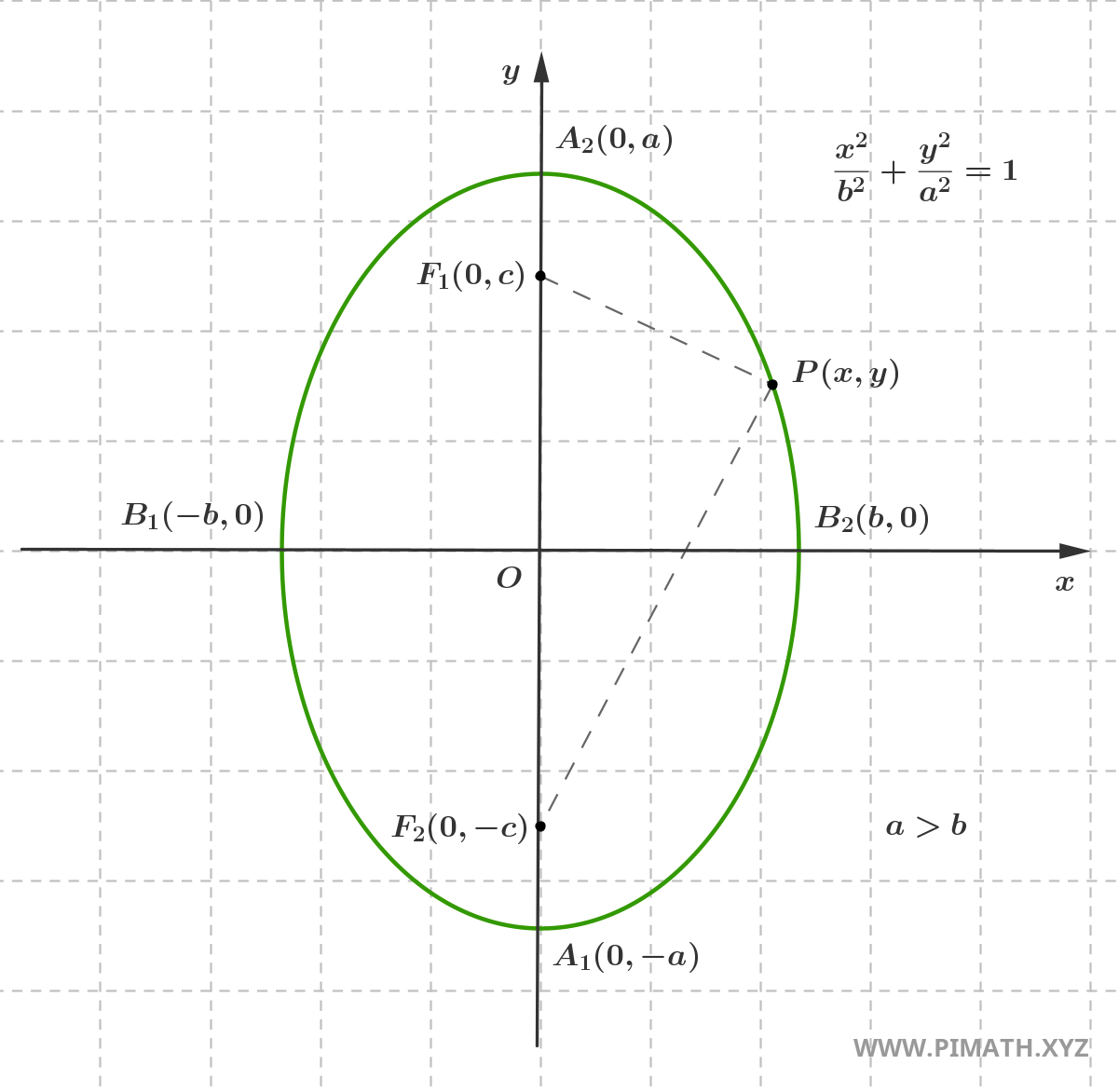
In this case, imposing \( |PF_1| + |PF_2| = 2a \) and with analogous algebraic steps, the ellipse equation becomes:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \]
This change reflects a 90-degree rotation of the ellipse with respect to the x-axis. The form of the equation remains the same, but the axis along which the ellipse extends changes.
In this case as well, the center of the ellipse remains at the origin and the geometric definition remains valid: for every point \( P(x, y) \) on the ellipse, the sum of distances from the foci (which are now positioned along the y-axis) is always equal to \( 2a \).
How to Find the Equation of a Translated Ellipse
So far we have considered an ellipse with center at the origin and foci on the x-axis. However, an ellipse can be located at any point in the plane. In such cases, we speak of a translated ellipse.
Suppose the center of the ellipse is at point \( C(x_0, y_0) \). The standard equation is modified accordingly, by translating the coordinates.
For the equation of a translated ellipse, it is essential to distinguish which is the semi-major axis and which is the semi-minor axis. Depending on the orientation of the ellipse with respect to the coordinate axes, the translated standard equation takes slightly different forms:
Horizontally Oriented Translated Ellipse
The major axis is parallel to the x-axis, so the foci lie along the line \( y = y_0 \)
In this case, the semi-major axis \( a \) is the value under the term \( (x - x_0)^2 \), and the semi-minor axis \( b \) is the value under the term \( (y - y_0)^2 \).
\[ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 \quad , \quad a > b \]
Vertically Oriented Translated Ellipse
The major axis is parallel to the y-axis, so the foci lie along the line \( x = x_0 \)
In this case, the semi-major axis \( a \) is the value under the term \( (y - y_0)^2 \), and the semi-minor axis \( b \) is the value under the term \( (x - x_0)^2 \).
\[ \frac{(x - x_0)^2}{b^2} + \frac{(y - y_0)^2}{a^2} = 1 \quad , \quad a > b \]
Note: The foci are no longer on the coordinate axes x or y, but on lines parallel to these, passing through the center \( (x_0, y_0) \).
Relationship between ellipse parameters
In the case of an ellipse with center at the origin and axes parallel to the coordinate axes, the relationship between the main parameters is given by a fundamental formula that connects the semi-major axis \( a \), the semi-minor axis \( b \), and the distance of the foci from the center \( c \).
The formula is as follows:
\[ c^2 = a^2 - b^2 \]
Therefore, the distance of the foci from the center can be calculated as:
\[ c = \sqrt{a^2 - b^2} \]
This relationship is valid for all ellipses with center at the origin and axes aligned with the coordinate axes, where \( a > b \). The semi-major axis is always associated with the axis having the larger denominator in the standard equation of the ellipse:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , a > b \quad \text{(if the major axis is horizontal)} \]
On the other hand:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \quad \text{(if the major axis is vertical)} \]
In this case, \( c^2 = a^2 - b^2 \) and thus \( c = \sqrt{a^2 - b^2} \). Knowing these relationships allows us to quickly calculate the position of the foci and better understand the geometry of the ellipse.
Eccentricity of an Ellipse: Definition, Geometric Meaning and Formula
Eccentricity is a fundamental measure that allows us to understand how much an ellipse deviates from a circle. Every ellipse has two foci: they are two interior points such that the sum of distances from any point on the ellipse to the two foci is constant. Eccentricity, denoted by the letter \( e \), is a number that varies from \( 0 \) to \( 1 \) and describes the shape of the ellipse.
Definition of Eccentricity
Eccentricity \( e \) is not a value chosen arbitrarily, but a value that emerges naturally from the geometric properties of the ellipse. In particular, if \( a \) is the length of the semi-major axis and \( b \) is that of the semi-minor axis, then the distance \( c \) between the center and one of the foci is: \[c = \sqrt{a^2 - b^2}\] With \( a > b \), eccentricity is always given by the following formula: \[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1-\frac{b^2}{a^2}}\] This formula is valid whether the major axis is horizontal or vertical, since \( a \) always represents the semi-major axis regardless of the orientation of the ellipse.
Geometric Meaning of Eccentricity
When eccentricity equals zero, that is \( e = 0 \), it means that the two foci coincide at the center of the ellipse. In this case the ellipse is actually a circle, because all radii (that is, the segments connecting the center to a point on the curve) have the same length: \( a = b \).
When instead eccentricity is a number between \( 0 \) and \( 1 \), that is \( 0 < e < 1 \), the ellipse is elongated. The greater the value of \( e \), the more the foci move away from the center and the more the ellipse appears elongated along the major axis and compressed along the minor axis.
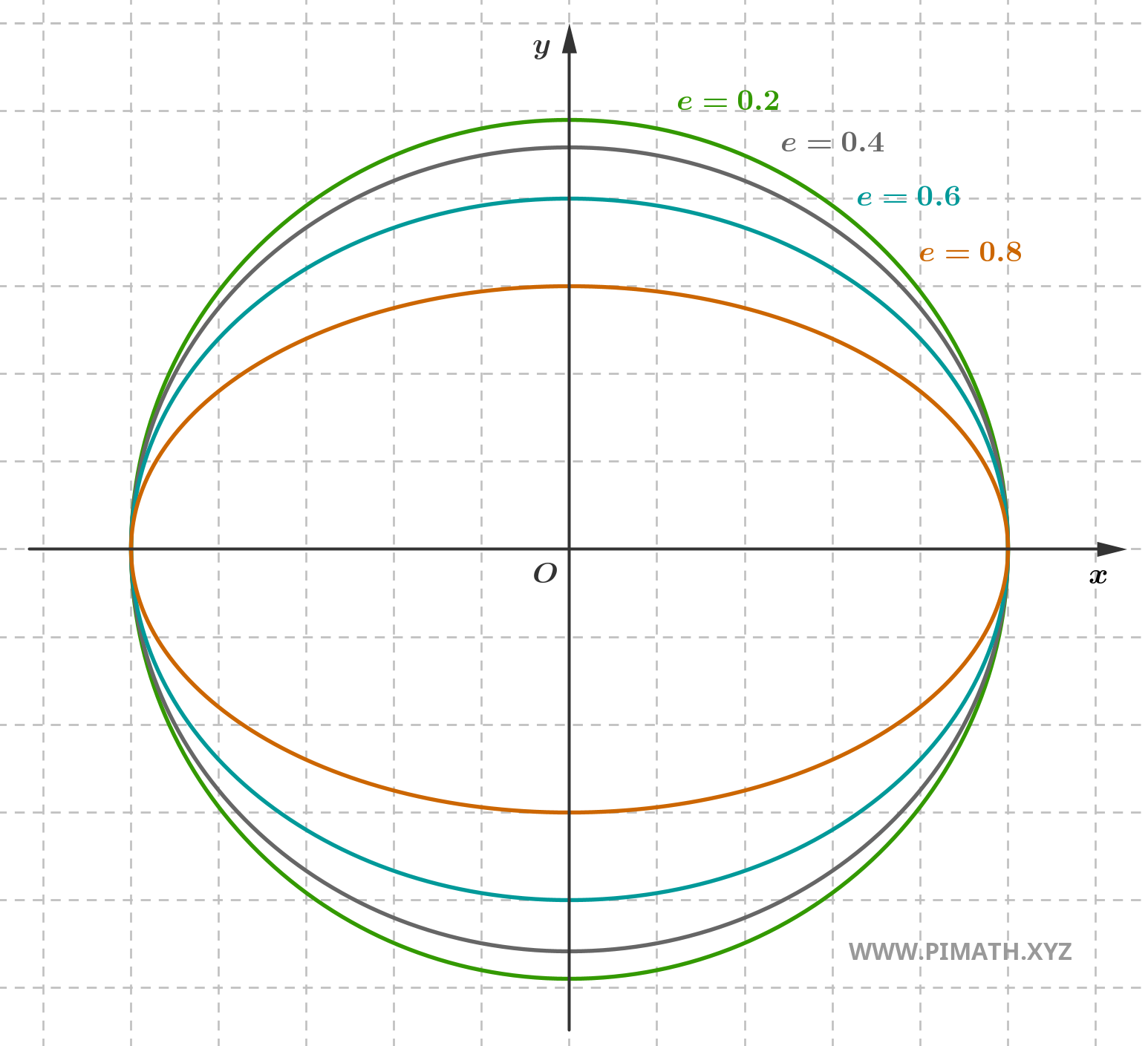
Finally, when \( e \) approaches \( 1 \), the shape of the ellipse becomes extremely elongated and the foci are very distant from the center.
For example, let us consider an ellipse with semi-major axis \( a = 5 \) and semi-minor axis \( b = 3 \).
We first calculate the distance of the foci from the center:
\[c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4\]
At this point we can calculate the eccentricity:
\[e = \frac{4}{5} = 0.8\]
The value we found indicates that the ellipse is quite flattened and the foci are well separated from the center. Here is the graph:
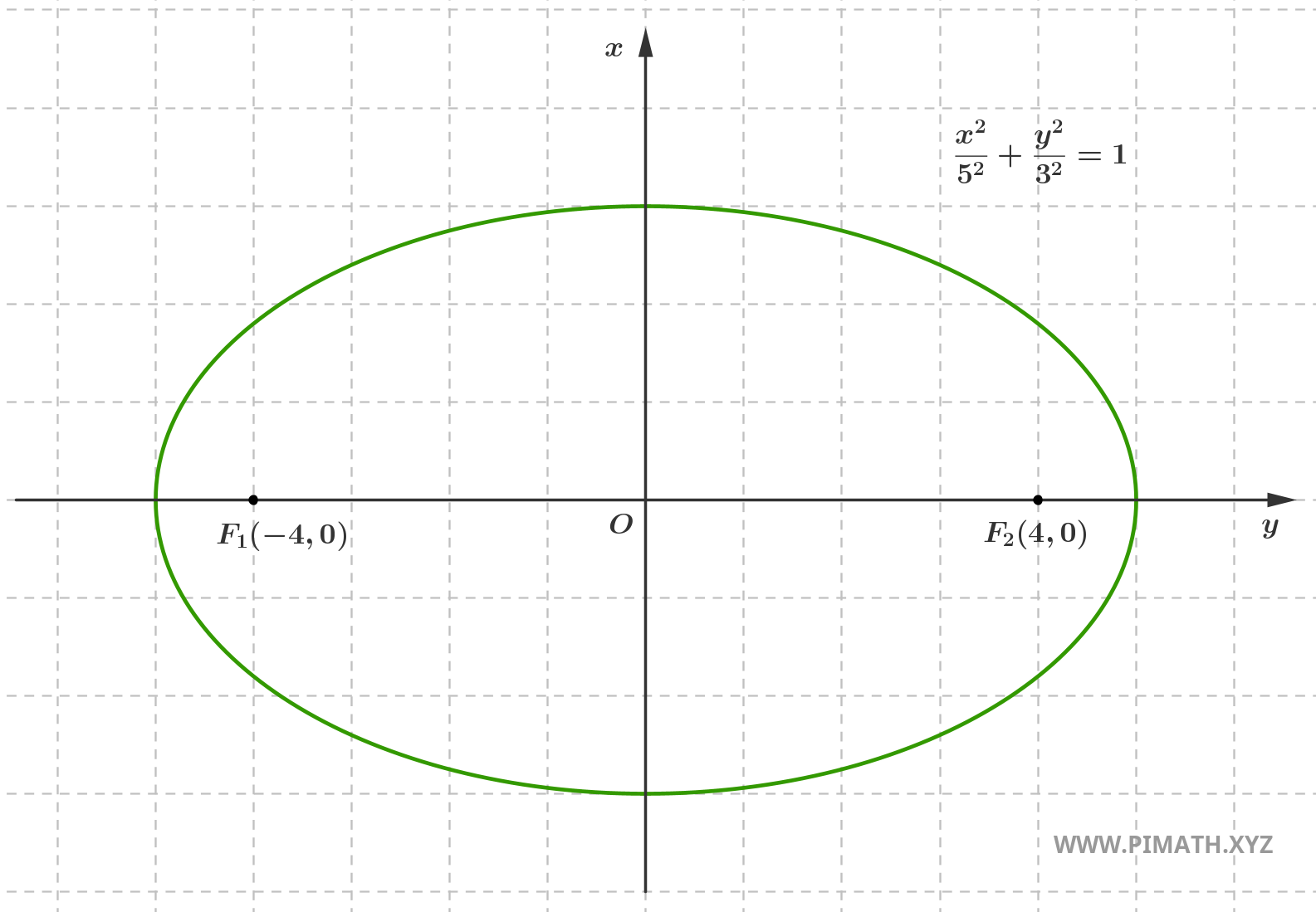
The eccentricity of an ellipse is a concept that relates the position of the foci to the overall shape of the curve. It is not just a formula to memorize, but a useful tool for visually understanding how close the ellipse is to a circle or how elongated it is. Remember: the closer \( e \) is to zero, the more the ellipse resembles a circle. The closer \( e \) is to \( 1 \), the more flattened it is and the farther the foci are.
Solved Exercises
Exercise 1. Verify whether point \( P(3, 2) \) belongs to the ellipse with equation:
\[ \frac{x^2}{9} + \frac{y^2}{4} = 1 \]
Solution. We substitute \( x = 3 \), \( y = 2 \):
\[ \frac{3^2}{9} + \frac{2^2}{4} = \frac{9}{9} + \frac{4}{4} = 1 + 1 = 2 \neq 1 \]
This means that the point does not belong to the ellipse.
Exercise 2. An ellipse has center at the origin, horizontal major axis, semi-major axis \( a = 5 \) and semi-minor axis \( b = 3 \). Find the equation of the ellipse.
Solution. The standard equation is
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{9} = 1 \]
Exercise 3. Determine the position of the foci of the ellipse with equation:
\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]
Find the focal distance \( c \).
Solution. From the equation \( \displaystyle \frac{x^2}{16} + \displaystyle \frac{y^2}{9} = 1 \), we identify that the larger term (16) is under \( x^2 \), so the major axis is horizontal.
According to our convention: \( a^2 = 16 \), \( b^2 = 9 \), therefore \( a = 4 \), \( b = 3 \).
We calculate the focal distance \( c \) using:
\[ c^2 = a^2 - b^2 = 16 - 9 = 7 \Rightarrow c = \sqrt{7} \]
The foci are located at points \( F_1(-\sqrt{7}, 0) \), \( F_2(\sqrt{7}, 0) \).
Exercise 4. Write the standard equation of the ellipse with center at the origin, vertical major axis, knowing that the vertices are located at points \( (0, \pm 6) \) and the foci are located at points \( (0, \pm 4) \).
Solution. If the vertices are at \( (0, \pm 6) \), then the semi-major axis is \( a = 6 \), therefore \( a^2 = 36 \).
The foci are at \( (0, \pm 4) \), therefore \( c = 4 \), therefore \( c^2 = 16 \).
We calculate:
\[ b^2 = a^2 - c^2 = 36 - 16 = 20 \]
The equation of the ellipse, with vertical major axis, is: \[ \displaystyle \frac{x^2}{b^2} + \displaystyle \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{20} + \frac{y^2}{36} = 1 \]
Exercise 5. An ellipse has foci at points \( F_1(-3,0) \) and \( F_2(3,0) \), and passes through point \( P(4,1) \). Find the standard equation of the ellipse.
Solution. The foci are \( F_1(-3, 0) \), \( F_2(3, 0) \). Then \( c = 3 \), therefore \( c^2 = 9 \).
Point \( P(4, 1) \) belongs to the ellipse. By definition: \[ |PF_1| + |PF_2| = 2a \] We calculate: \[ |PF_1| = \sqrt{(4 - (-3))^2 + (1 - 0)^2} = \sqrt{7^2 + 1^2} = \sqrt{49 + 1} = \sqrt{50} = 5\sqrt{2} \] \[ |PF_2| = \sqrt{(4 - 3)^2 + (1 - 0)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \] \[ \Rightarrow |PF_1| + |PF_2| = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \] \[ \Rightarrow 2a = 6\sqrt{2} \Rightarrow a = 3\sqrt{2} \Rightarrow a^2 = (3\sqrt{2})^2 = 9 \cdot 2 = 18 \] \[ b^2 = a^2 - c^2 = 18 - 9 = 9 \] The equation of the ellipse is therefore: \[ \frac{x^2}{18} + \frac{y^2}{9} = 1 \]

