Equation of the Circle: Formulas, Proofs and Solved Exercises

The circle is the locus of points in the plane that are at a constant distance from a fixed point, called the center. This constant distance is called the radius. The circle is a closed curve, symmetric with respect to its center, and is a particular case of a degenerate conic obtained by intersecting a circular cone with a plane perpendicular to the axis of the cone.

Table of Contents

• Geometric Definition and Equation Derivation
• Equation of the Circle with Center at the Origin
• Equation of the Circle with General Center
• General Form and Completing the Square
• Conditions for Representing a Real Circle
• Position of a Point with Respect to the Circle
• Tangent Line to the Circle
• Intersection of Two Circles
• Pencil of Circles
• Symmetries and Geometric Properties
• Solved Exercises

Consider a fixed point \( C(x_0, y_0) \) in the orthogonal Cartesian plane. The circle with center \( C \) and radius \( r > 0 \) is the set of points \( P(x, y) \) in the plane such that:

\[ d = \text{dist}(P, C) = r \]

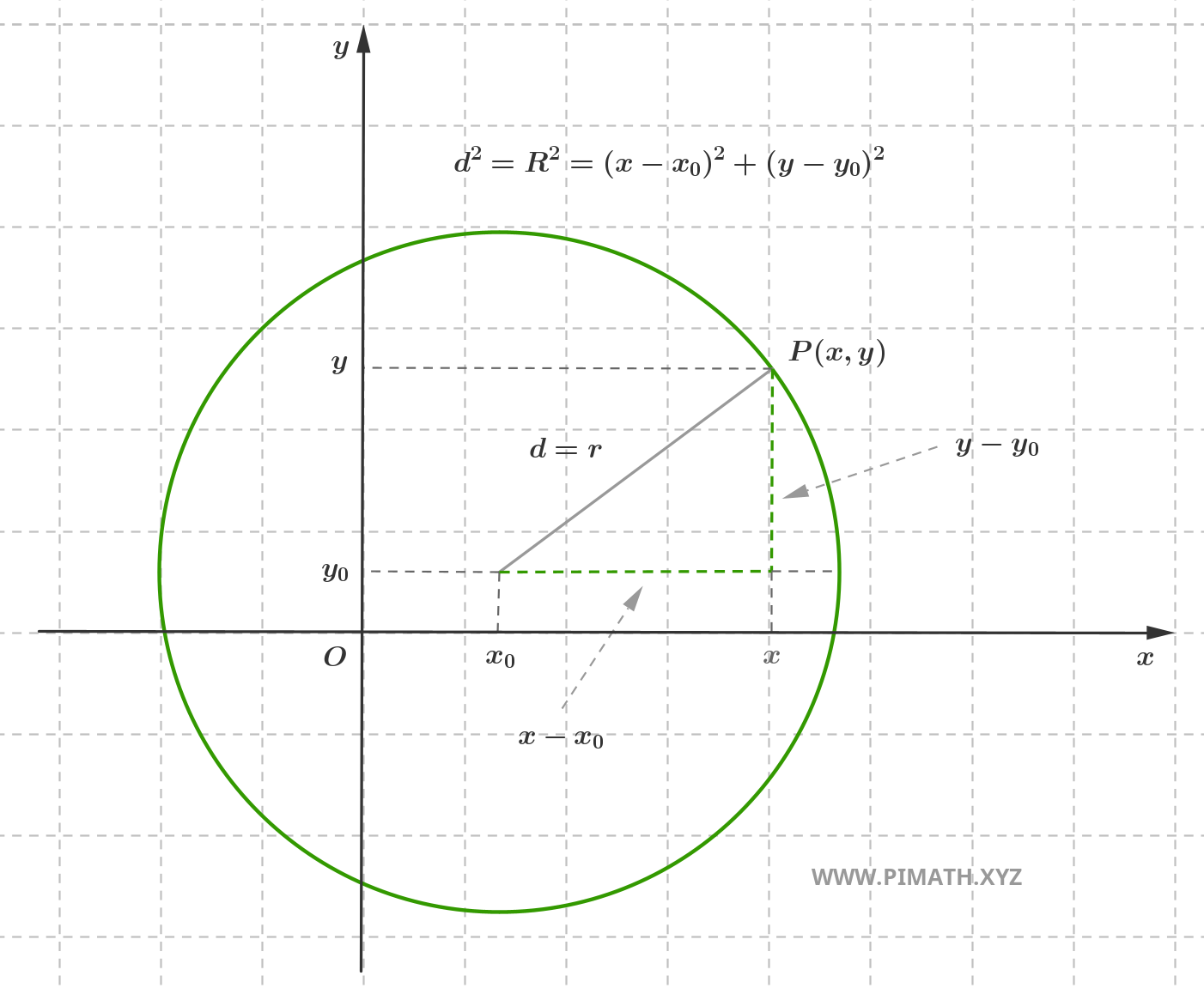
Applying the Euclidean distance formula between two points in the Cartesian plane, we have:

\[ \text{dist}(P, C) = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]

Imposing the condition \( \text{dist}(P, C) = r \), we obtain:

\[ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r \]

Squaring both sides (a valid operation since both sides are non-negative, with \( r > 0 \) by definition):

\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]

This is the canonical form (or standard form) of the equation of the circle with center \( C(x_0, y_0) \) and radius \( r \). The equation represents all and only those points that satisfy the geometric condition of belonging to the circle.

In the particular case where the center coincides with the origin of the coordinate system, that is \( C(0, 0) \), setting \( x_0 = 0 \) and \( y_0 = 0 \) in the canonical form, the equation simplifies considerably:

\[ x^2 + y^2 = r^2 \]

This is the most elementary equation of the circle and describes the set of all points equidistant from the origin of the Cartesian axes. The equation enjoys the following symmetry properties:

• Symmetry with respect to the x-axis: if \( (x, y) \) belongs to the circle, then \( (x, -y) \) also belongs to it
• Symmetry with respect to the y-axis: if \( (x, y) \) belongs to the circle, then \( (-x, y) \) also belongs to it
• Central symmetry with respect to the origin: if \( (x, y) \) belongs to the circle, then \( (-x, -y) \) also belongs to it

Furthermore, all diameters of the circle pass through the origin and have length \( 2r \). The point \( (r, 0) \) represents the intersection of the circle with the positive x-axis.

Let us now consider the general case of a circle with center at an arbitrary point \( C(x_0, y_0) \) in the plane and radius \( r > 0 \). The canonical equation is:

\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]

Expanding the squares of the binomials using the algebraic identities \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \), we obtain:

\[ x^2 - 2x \cdot x_0 + x_0^2 + y^2 - 2y \cdot y_0 + y_0^2 = r^2 \]

Rearranging terms and moving all quantities to the left side:

\[ x^2 + y^2 - 2x_0 x - 2y_0 y + (x_0^2 + y_0^2 - r^2) = 0 \]

We now introduce the parameters:

\[ D = -2x_0 \quad , \quad E = -2y_0 \quad , \quad F = x_0^2 + y_0^2 - r^2 \]

From these relations we can derive:

\[ x_0 = -\frac{D}{2} \quad , \quad y_0 = -\frac{E}{2} \quad , \quad r^2 = x_0^2 + y_0^2 - F = \frac{D^2 + E^2}{4} - F \]

Substituting into the expanded form, we obtain the general form of the circle equation:

\[ x^2 + y^2 + Dx + Ey + F = 0 \]

Given an equation in general form:

\[ x^2 + y^2 + Dx + Ey + F = 0 \]

to convert it to canonical form and determine the center and radius, we use the technique of completing the square. The method consists of transforming the expressions \( x^2 + Dx \) and \( y^2 + Ey \) into perfect squares.

For the term in \( x \):

\[ x^2 + Dx = x^2 + Dx + \frac{D^2}{4} - \frac{D^2}{4} = \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} \]

Similarly, for the term in \( y \):

\[ y^2 + Ey = y^2 + Ey + \frac{E^2}{4} - \frac{E^2}{4} = \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} \]

Substituting into the general equation:

\[ \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} + \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} + F = 0 \]

Rearranging:

\[ \left( x + \frac{D}{2} \right)^2 + \left( y + \frac{E}{2} \right)^2 = \frac{D^2 + E^2}{4} - F \]

This is the canonical form, from which we can directly read:

• Center: \( C\left( -\displaystyle \frac{D}{2}, -\displaystyle\frac{E}{2} \right) \)
• Radius: \( r = \sqrt{\displaystyle\frac{D^2 + E^2}{4} - F} \) (provided the expression under the square root is positive)

An equation of the form:

\[ ax^2 + by^2 + cxy + dx + ey + f = 0 \]

represents a circle if and only if the following conditions are satisfied:

1. Equal coefficients of quadratic terms: \( a = b \neq 0 \)
2. Absence of the mixed term: \( c = 0 \)
3. Positive discriminant: \( \Delta = \displaystyle \frac{d^2 + e^2}{4a^2} - \displaystyle \frac{f}{a} > 0 \)

In the case of the standard form \( x^2 + y^2 + Dx + Ey + F = 0 \), the condition reduces to:

\[ \frac{D^2 + E^2}{4} - F > 0 \quad \Leftrightarrow \quad D^2 + E^2 - 4F > 0 \]

We distinguish three cases:

• If \( D^2 + E^2 - 4F > 0 \): the equation represents a real circle with radius \( r = \displaystyle \frac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
• If \( D^2 + E^2 - 4F = 0 \): the equation represents a degenerate circle (a point)
• If \( D^2 + E^2 - 4F < 0 \): the equation has no real solutions (imaginary circle)

Given a circle with equation \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) and a point \( P(x_P, y_P) \), we can determine the relative position of the point with respect to the circle by calculating the quantity:

\[ \delta = (x_P - x_0)^2 + (y_P - y_0)^2 - r^2 \]

There are three possibilities:

• If \( \delta = 0 \): the point lies on the circle
• If \( \delta < 0 \): the point is inside the circle
• If \( \delta > 0 \): the point is outside the circle

Equivalently, by comparing the distance \( d = \sqrt{(x_P - x_0)^2 + (y_P - y_0)^2} \) of the point from the center with the radius:

• If \( d = r \): point on the circle
• If \( d < r \): point inside
• If \( d > r \): point outside

Given a circle with center \( C(x_0, y_0) \) and radius \( r \), and a point \( P(x_1, y_1) \) lying on the circle, the equation of the tangent line to the circle at point \( P \) is:

\[ (x_1 - x_0)(x - x_0) + (y_1 - y_0)(y - y_0) = r^2 \]

In the particular case of a circle centered at the origin \( x^2 + y^2 = r^2 \), the equation of the tangent at point \( P(x_1, y_1) \) simplifies to:

\[ x_1 x + y_1 y = r^2 \]

The tangent line is perpendicular to the radius drawn to the point of tangency. This result follows from the fact that the vector \( \overrightarrow{CP} = (x_1 - x_0, y_1 - y_0) \) is normal to the tangent.

Tangents from an External Point

From an external point \( P(x_P, y_P) \) to a circle, exactly two tangent lines can be drawn. The points of tangency are obtained by solving the system formed by the equation of the circle and the condition that the distance from the center to the line equals the radius.

Given two circles:

\[ \Gamma_1: \quad x^2 + y^2 + D_1 x + E_1 y + F_1 = 0 \] \[ \Gamma_2: \quad x^2 + y^2 + D_2 x + E_2 y + F_2 = 0 \]

To find the intersection points, we solve the system formed by the two equations. Subtracting the second from the first, we obtain the equation of the radical axis:

\[ (D_1 - D_2)x + (E_1 - E_2)y + (F_1 - F_2) = 0 \]

The radical axis is a line that, when the circles intersect, passes through the two intersection points. The relative positions of the circles depend on the distance \( d \) between the centers and the radii \( r_1, r_2 \):

• If \( d > r_1 + r_2 \): circles are external (no intersection)
• If \( d = r_1 + r_2 \): circles are externally tangent (one intersection point)
• If \( |r_1 - r_2| < d < r_1 + r_2 \): circles are secant (two intersection points)
• If \( d = |r_1 - r_2| \): circles are internally tangent (one intersection point)
• If \( d < |r_1 - r_2| \): one circle is inside the other (no intersection)

A pencil of circles is a set of circles depending on a parameter. The pencil generated by two circles \( \Gamma_1 \) and \( \Gamma_2 \) has equation:

\[ \lambda \Gamma_1 + \mu \Gamma_2 = 0 \]

where \( \lambda \) and \( \mu \) are real parameters, not both zero. Explicitly:

\[ \lambda(x^2 + y^2 + D_1 x + E_1 y + F_1) + \mu(x^2 + y^2 + D_2 x + E_2 y + F_2) = 0 \]

We distinguish different types of pencils:

• Elliptic pencil: the base circles do not intersect; all circles in the pencil are real
• Parabolic pencil: the base circles are tangent; the pencil contains lines (degenerate circles)
• Hyperbolic pencil: the base circles intersect at two points; the pencil contains both real and imaginary circles

The circle possesses remarkable symmetry properties that make it a geometric figure of particular interest:

Symmetries

• Central symmetry: every circle is symmetric with respect to its center
• Axes of symmetry: every line passing through the center is an axis of symmetry
• Rotational invariance: the circle is invariant under any rotation about its center

Metric Properties

• Circumference: \( C = 2\pi r \)
• Area of the disk: \( A = \pi r^2 \)
• Central and inscribed angles: an inscribed angle is half of the corresponding central angle

Exercise 1. Verify whether the point \( P(3, 4) \) lies on the circle with equation \( x^2 + y^2 = 25 \).

Solution. We substitute the coordinates of the point into the equation:

\[ 3^2 + 4^2 = 9 + 16 = 25 \]

Since the equality is satisfied, the point \( P(3, 4) \) lies on the circle. Geometrically, this means that the distance from \( P \) to the origin is exactly equal to the radius \( r = 5 \).

Exercise 2. Determine the equation of the circle with center \( C(2, -3) \) and radius \( r = 4 \).

Solution. Applying the canonical form:

\[ (x - 2)^2 + (y - (-3))^2 = 4^2 \] \[ (x - 2)^2 + (y + 3)^2 = 16 \]

Expanding, we obtain the general form:

\[ x^2 - 4x + 4 + y^2 + 6y + 9 = 16 \] \[ x^2 + y^2 - 4x + 6y - 3 = 0 \]

Exercise 3. Given the equation \( x^2 + y^2 + 6x - 8y + 5 = 0 \), determine the center and radius of the circle.

Solution. We complete the squares:

\[ x^2 + 6x = (x + 3)^2 - 9 \] \[ y^2 - 8y = (y - 4)^2 - 16 \]

Substituting:

\[ (x + 3)^2 - 9 + (y - 4)^2 - 16 + 5 = 0 \] \[ (x + 3)^2 + (y - 4)^2 = 20 \]

Therefore:

• Center: \( C(-3, 4) \)
• Radius: \( r = \sqrt{20} = 2\sqrt{5} \)

Exercise 4. Find the equation of the circle passing through the points \( A(1, 0) \), \( B(0, 1) \), and \( C(-1, 0) \).

Solution. We use the general form \( x^2 + y^2 + Dx + Ey + F = 0 \) and impose passage through the three points:

For \( A(1, 0) \):

\[ 1 + 0 + D + 0 + F = 0 \implies D + F = -1 \]

For \( B(0, 1) \):

\[ 0 + 1 + 0 + E + F = 0 \implies E + F = -1 \]

For \( C(-1, 0) \):

\[ 1 + 0 - D + 0 + F = 0 \implies -D + F = -1 \]

Solving the system:

\[ \begin{cases} D + F = -1 \\ E + F = -1 \\ -D + F = -1 \end{cases} \]

From the first and third equations: \( D = 0 \), therefore \( F = -1 \). From the second equation: \( E = 0 \).

The desired equation is: \( x^2 + y^2 - 1 = 0 \), or \( x^2 + y^2 = 1 \).

This is the unit circle centered at the origin.

Exercise 5. Determine the tangent lines to the circle \( x^2 + y^2 = 9 \) drawn from the external point \( P(5, 0) \).

Solution. Let \( T(x_T, y_T) \) be a point of tangency. The line \( PT \) has the equation of the tangent at point \( T \):

\[ x_T x + y_T y = 9 \]

Since this line passes through \( P(5, 0) \):

\[ 5x_T + 0 \cdot y_T = 9 \Rightarrow x_T = \frac{9}{5} \]

Since \( T \) is on the circle: \( x_T^2 + y_T^2 = 9 \), therefore:

\[ \left(\frac{9}{5}\right)^2 + y_T^2 = 9 \Rightarrow y_T^2 = 9 - \frac{81}{25} = \frac{144}{25} \Rightarrow y_T = \pm\frac{12}{5} \]

The points of tangency are:

\[ T_1\left(\frac{9}{5}, \frac{12}{5}\right) \quad \text{and} \quad T_2\left(\frac{9}{5}, -\frac{12}{5}\right) \]

The equations of the tangent lines are:

\[ \frac{9}{5}x + \frac{12}{5}y = 9 \quad \implies \quad 3x + 4y = 15 \] \[ \frac{9}{5}x - \frac{12}{5}y = 9 \quad \implies \quad 3x - 4y = 15 \]