Equation of Line

Let \( P_1(x_1,y_1) \) and \( P_2(x_2,y_2) \) be two distinct points in the Cartesian plane. The line passing through these two points has the equation:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

By multiplying both sides by \( y_2 - y_1 \), it becomes:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

• Similarity of Triangles
• Geometric Interpretation
• Transformation into Explicit Equation
• Explicit Form of the Line
• Slope of the Line
• Interpretation of the Slope
• Implicit Form of the Line
• Parametric Equation of the Line
• Perpendicular Line
• Exercises

To prove the equation of the line passing through two points, consider the distinct points \( P_1(x_1,y_1) \) and \( P_2(x_2,y_2) \) in the Cartesian plane. We want to show that the equation:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

is satisfied by every point \( P(x,y) \) lying on the line.

Consider the triangles in the figure. They are similar by the common angle criterion (the angle between the line and the x-axis) and by the proportionality of the corresponding sides:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

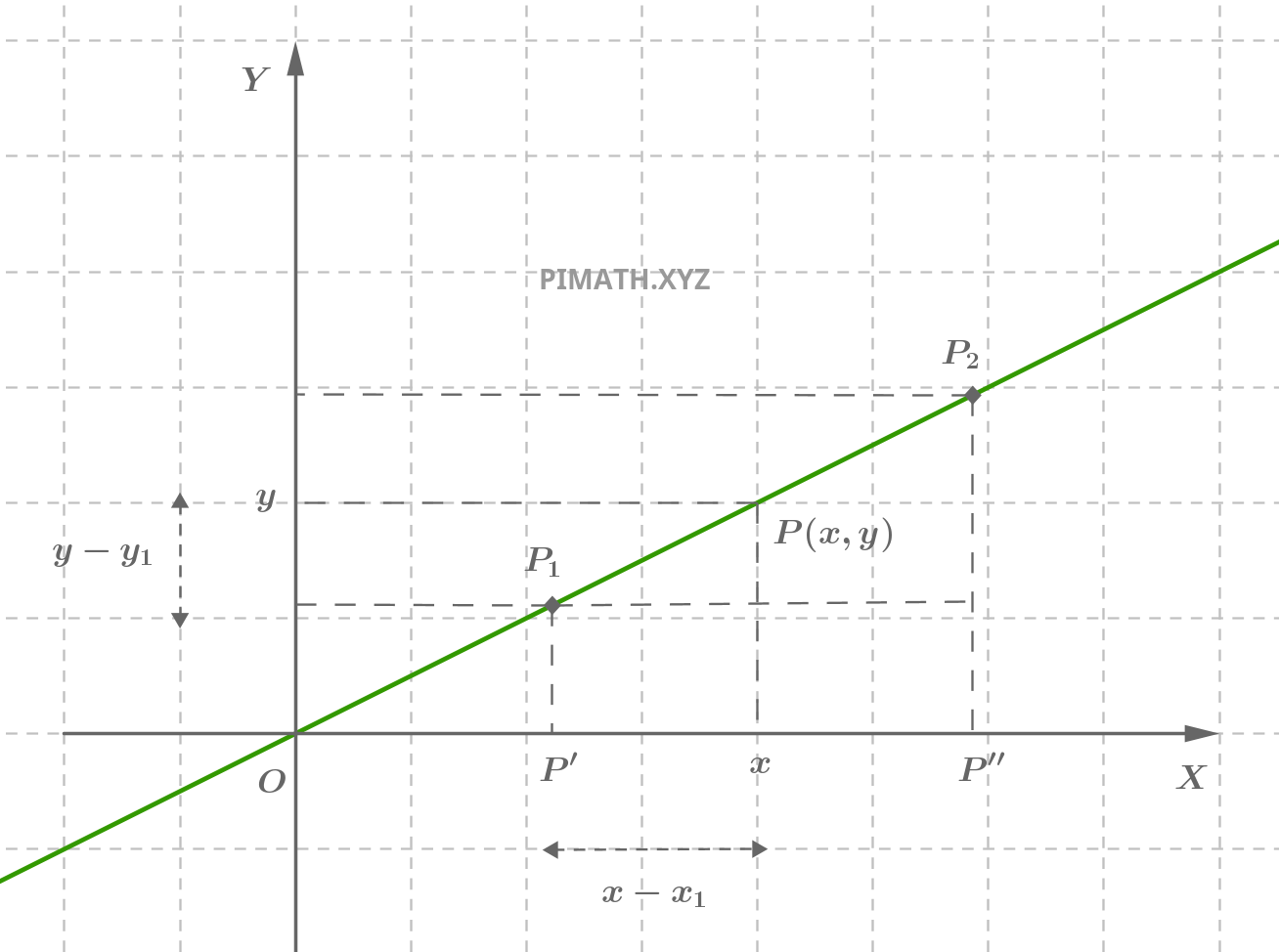
This relationship follows directly from the property of the similarity of triangles, ensuring that the ratio of the differences in the y-coordinates and x-coordinates remains constant along the line.

The fraction \( \displaystyle \frac{y - y_1}{y_2 - y_1} \) represents the ratio between the height of the generic point \( P \) relative to \( P_1 \) and the total height between \( P_1 \) and \( P_2 \). Similarly, \( \displaystyle \frac{x - x_1}{x_2 - x_1} \) measures the analogous ratio for the x-coordinates. The equality of these two ratios indicates that the point \( P \) is aligned with \( P_1 \) and \( P_2 \), meaning it lies on the line passing through these two points.

By multiplying both sides by \( y_2 - y_1 \), we get:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

which is the explicit form of the line equation \( y = mx + q \), with slope \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \).

This form of the equation is fundamental for describing the linear relationship between \( x \) and \( y \) for all points on the line passing through \( P_1 \) and \( P_2 \).

The equation of the line passing through two distinct points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) can be expressed in explicit form as follows:

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) \]

This equation relates the variable \( y \) to the variable \( x \) along the line. In other words, for any chosen value of \( x \), the equation allows us to determine the corresponding value of \( y \), which is the coordinate of the point on the line.

In the context of this equation, the term:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

represents the slope of the line, or the slope coefficient. The slope is a measure of the line's inclination relative to the x-axis. If the slope is positive, the line is increasing (rising from left to right); if it is negative, the line is decreasing (falling from left to right).

In other words, the slope describes how quickly the line rises or falls in relation to the horizontal axis \( x \). The slope is a crucial parameter for determining the orientation of the line in the Cartesian plane.

The slope \( m \) of a line passing through two points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) is given by the formula:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

The slope measures the inclination of the line relative to the x-axis \( x \). Depending on the value of the slope, we can make the following observations:

• If \( m > 0 \), the line is increasing, meaning it rises from left to right. This means that for each increment in \( x \), \( y \) also increases. The line forms an acute angle with the \( x \)-axis.
• If \( m < 0 \), the line is decreasing, meaning it falls from left to right. In this case, for each increment in \( x \), the value of \( y \) decreases. The line forms an obtuse angle with the \( x \)-axis.
• If \( x_2 = x_1 \), the slope is undefined, which implies that the line is vertical. In this case, there is no horizontal change (the difference between the x-coordinates \( x_2 - x_1 \) is zero), so the slope cannot be numerically defined. The line is parallel to the \( y \)-axis and has no horizontal inclination.

In general, the slope \( m \) provides important information about the behavior of the line. If the line is increasing, the value of \( y \) increases as \( x \) increases; if it is decreasing, the value of \( y \) decreases as \( x \) increases; if the line is vertical, it means that \( y \) does not depend on \( x \), and the line has no horizontal inclination.

Starting from the explicit form of the line equation:

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

we can multiply both sides by \( x_2 - x_1 \) to obtain a more general version and rewrite the equation as follows:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

By multiplying both sides of the equation by \( (x_2 - x_1) \), we get:

\[ (y - y_1)(x_2 - x_1) = (y_2 - y_1)(x - x_1) \]

Expanding the terms, we get:

\[ (x_2 - x_1) y - (x_2 - x_1) y_1 = (y_2 - y_1) x - (y_2 - y_1) x_1 \]

Now, to obtain an implicit form, we want to collect the terms so that the equation is in a linear form that does not explicitly solve for \( y \). We move the terms containing \( y \) and \( x \) to one side and the other terms to the other side:

\[ (y_2 - y_1) x - (x_2 - x_1) y = (y_2 - y_1) x_1 - (x_2 - x_1) y_1 \]

We write this equation in the standard implicit form:

\[ (y_2 - y_1) x - (x_2 - x_1) y + ((x_2 - x_1) y_1 - (y_2 - y_1) x_1) = 0 \]

This is the implicit form of the line equation. If we define the coefficients as \( a = y_2 - y_1 \), \( b = -(x_2 - x_1) \), and \( c = (x_2 - x_1) y_1 - (y_2 - y_1) x_1 \), the equation takes the general form:

\[ ax + by + c = 0. \]

Alternatively, if we introduce the slope \( m = \frac{y_2 - y_1}{x_2 - x_1} \) and rearrange the terms in the previous equation, we can write:

\[ m(x_2 - x_1)x - (x_2 - x_1)y + ((x_2 - x_1)y_1 - m(x_2 - x_1)x_1) = 0 \]

Simplifying and dividing by \( (x_2 - x_1) \), we get:

\[ mx - y + (y_1 - mx_1) = 0. \]

In this form, the coefficients are \( a = m \), \( b = -1 \), and \( c = y_1 - mx_1 \).

The implicit form \( ax + by + c = 0 \) is a more general representation of a line in the Cartesian plane. This format is particularly useful for geometric and algebraic applications, where the explicit value of \( y \) is not required or when we want to work directly with the algebraic properties of the line.

The line passing through the points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) can also be described in parametric form. In this representation, the coordinates \( x \) and \( y \) of a point on the line are expressed as a function of a real parameter \( t \), which varies along the line.

The parametric equation of the line is given by:

\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]

Here, \( t \) is the parameter that can take any real value. As \( t \) changes, the point \( (x, y) \) moves along the line connecting the two points \( P_1 \) and \( P_2 \).

The parametric form thus represents a family of points on the line, where the parameter \( t \) uniquely defines each point on the line. When \( t = 0 \), we obtain the point \( P_1(x_1, y_1) \); when \( t = 1 \), we obtain the point \( P_2(x_2, y_2) \). The values of \( t \) between 0 and 1 describe the points on the line between \( P_1 \) and \( P_2 \), while values of \( t \) greater than 1 or less than 0 extend the line beyond these points.

The parametric formula is based on the concept of a direction vector, which is the vector connecting \( P_1 \) and \( P_2 \). In fact, the difference \( (x_2 - x_1, y_2 - y_1) \) is the direction vector of the line, and the parameter \( t \) is the scaling factor that allows movement along the line.

In vector form, the parametric equation can be written as:

\[ \vec{r}(t) = \vec{P_1} + t \cdot (\vec{P_2} - \vec{P_1}), \]

where \( \vec{r}(t) \) represents the position of a generic point on the line at time \( t \), and \( \vec{P_1} \) and \( \vec{P_2} \) are the position vectors of the points \( P_1 \) and \( P_2 \), respectively.

The parametric form is particularly useful in various areas of analytic geometry, such as in the study of curves, computer graphics applications, or in physics to describe the motion of an object along a straight trajectory.

When two lines are perpendicular, their slopes are related by a specific relationship. If one line has slope \( m \), the slope of the perpendicular line is given by:

\[ m_\perp = -\frac{1}{m} \]

This formula expresses the fact that the product of the slopes of two perpendicular lines is equal to \(-1\). The reason for this relationship can be seen in the fact that the angles formed by the two lines must be 90° (a right angle), and thus the tangent of the angle between the lines must satisfy this condition.

To find the equation of the perpendicular line passing through a point \( (x_1, y_1) \), we can use the point-slope form. The slope of the perpendicular line is \( -\displaystyle \frac{1}{m} \), so the equation of the perpendicular line will be:

\[ y - y_1 = -\frac{1}{m} (x - x_1) \]

In this equation, \( (x_1, y_1) \) is the point through which the perpendicular line passes, and \( m \) is the slope of the original line. The formula describes a line that has the opposite and inverse slope compared to the original line.

If the original line is represented by the equation \( y = mx + q \), the perpendicular line will have the slope \( m_\perp = -\displaystyle \frac{1}{m} \) and will be written in the form \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), where \( (x_1, y_1) \) is the point of intersection between the original line and the perpendicular line.

This property of perpendicular lines is fundamental in many areas of geometry, trigonometry, and physics, especially when studying angles and perpendicular trajectories.

Exercise 1: Determine the equation of the line passing through \( A(1, 2) \) and \( B(3, 6) \).

Solution:

1. Calculate the slope of the line: \[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
2. Use the point-slope form to determine the equation of the line passing through \( A(1, 2) \) and with slope \( m = 2 \): \[ y - 2 = 2(x - 1). \]
3. Expanding the equation: \[ y - 2 = 2x - 2. \]
4. Simplifying: \[ y = 2x - 2 + 2 = 2x. \]

Therefore, the equation of the line passing through the points \( A(1, 2) \) and \( B(3, 6) \) is \[ y = 2x. \]

Verification: We can verify that both points satisfy this equation:

• For \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
• For \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]

Exercise 2: Write the parametric equation of the line passing through \( A(1, 2) \) and \( B(3, 6) \).

Solution:

1. Calculate the direction vector \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), which represents the direction of the line: \[ \boldsymbol{v} = (3 - 1, 6 - 2) = (2, 4). \]
2. The parametric equations of the line are: \[ \begin{cases} x = 1 + 2t \\ y = 2 + 4t \end{cases} \quad \text{with} \quad t \in \mathbb{R}. \]