Equation of the Parabola: Formulas, Proofs and Solved Exercises

The parabola is the locus of points in the plane for which the distance to a fixed point (focus) equals the distance to a fixed line (directrix). It has an axis of symmetry that passes through the focus and is perpendicular to the directrix. It is an open curve that is symmetric with respect to its own axis, with numerous applications in physics and geometry.

Table of Contents

• Canonical Equation of the Parabola
• Canonical Equation of a Parabola with Vertical or Horizontal Axis
• Translated Parabola in the Plane
• Vertex, Focus, Directrix and Axes of Symmetry
• Equation of the Parabola Given the Vertex and a Point
• Solved Exercises on the Parabola

A parabola is the locus of points \( P(x, y) \) in the plane that have the same distance to a fixed point, called the focus, and to a fixed line, called the directrix.

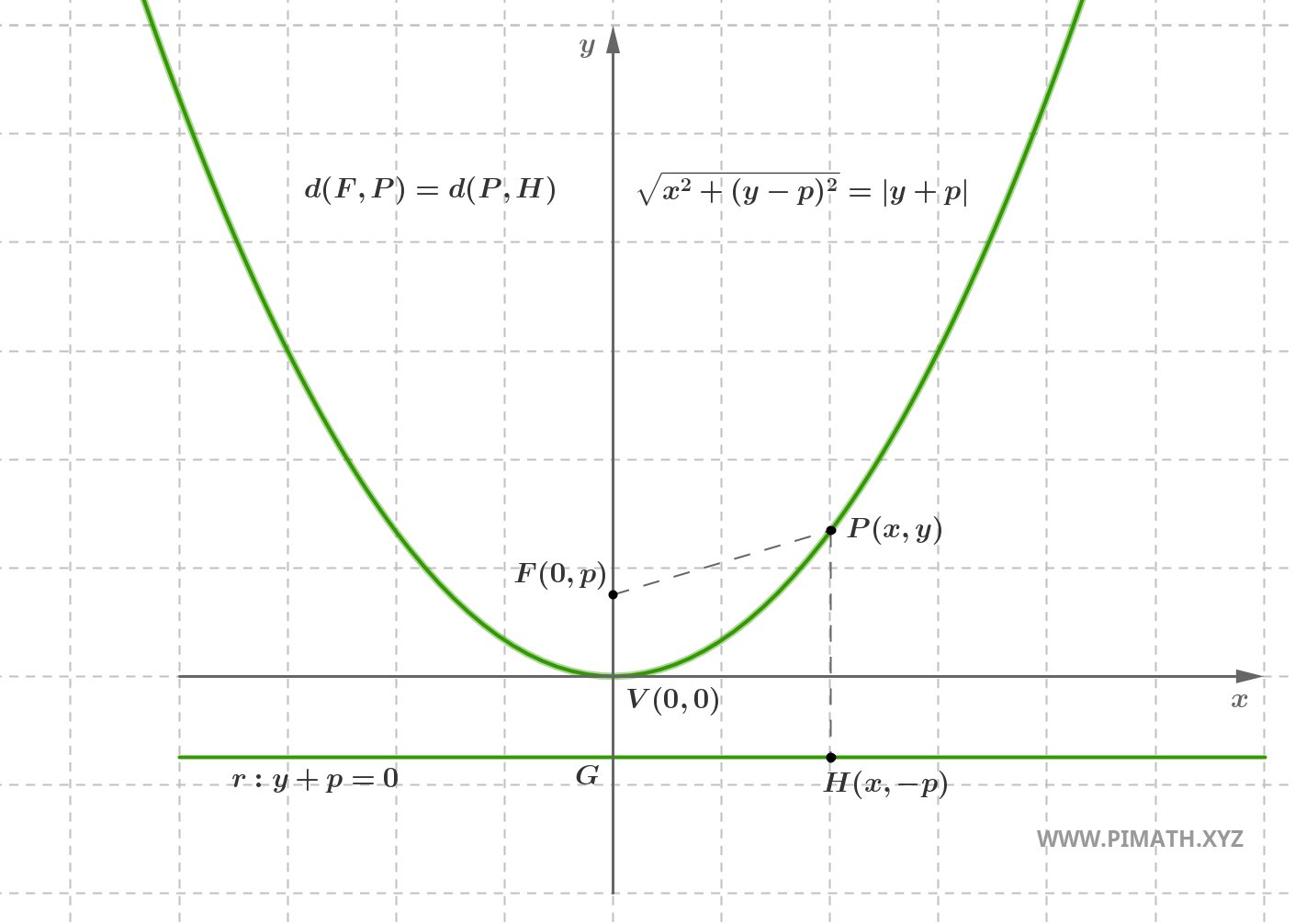
Let \( F(0, p) \) with \( p > 0 \) be the focus and let \( r \) be the directrix, with equation \( y = -p \). By definition, the points \( P(x, y) \) of the parabola satisfy:

\[ \text{d}(P, F) = \text{d}(P, r) \]

We calculate the distance between \( P(x, y) \) and the focus \( F(0, p) \):

\[ \text{d}(P, F) = \sqrt{(x - 0)^2 + (y - p)^2} = \sqrt{x^2 + (y - p)^2} \]

Now, we calculate the distance between \( P(x, y) \) and the directrix line \( y = -p \):

\[ \text{d}(P, r) = |y - (-p)| = |y + p| \]

Finally, we impose the equality between the two distances:

\[ \sqrt{x^2 + (y - p)^2} = |y + p| \]

Observation: since the parabola lies above the directrix (given that the focus is above the directrix for \( p > 0 \)), all points of the parabola satisfy \( y \geq -p \). Therefore \( y + p \geq 0 \) and we can remove the absolute value:

\[ \sqrt{x^2 + (y - p)^2} = y + p \]

We square both sides:

\[ x^2 + (y - p)^2 = (y + p)^2 \]

We expand the squares:

\[ x^2 + y^2 - 2py + p^2 = y^2 + 2py + p^2 \]

We simplify both sides:

\[ x^2 - 2py = 2py \]

We bring everything to the right side:

\[ x^2 = 4py \]

Finally, we divide by \( 4p \):

\[ y = \frac{1}{4p}x^2 \]

If we set \( a = \displaystyle \frac{1}{4p} \), we obtain the more compact form:

\[ y = ax^2 \]

which is the canonical equation of the parabola with vertex at the origin \( V(0, 0) \), focus at \( F(0, p) \) and directrix \( y = -p \).

In summary, the parabola with equation \( y = ax^2 \) has a vertical axis of symmetry, coinciding with the \( y \)-axis, and concavity directed upward if \( a > 0 \), or downward if \( a < 0 \).

The canonical equation of the parabola takes different forms depending on the orientation of the axis of symmetry. We distinguish two fundamental cases depending on whether the axis is vertical or horizontal.

Parabola with Vertical Axis

For a parabola with vertical axis of symmetry, parallel to the ordinate axis, the canonical equation is \( y = ax^2 \) or, in the equivalent form, \( x^2 = 4py \). In this configuration, the coefficient \( a = \displaystyle \frac{1}{4p} \) represents the leading coefficient, while \( p \) is the focal parameter that indicates the distance from the vertex to the focus.

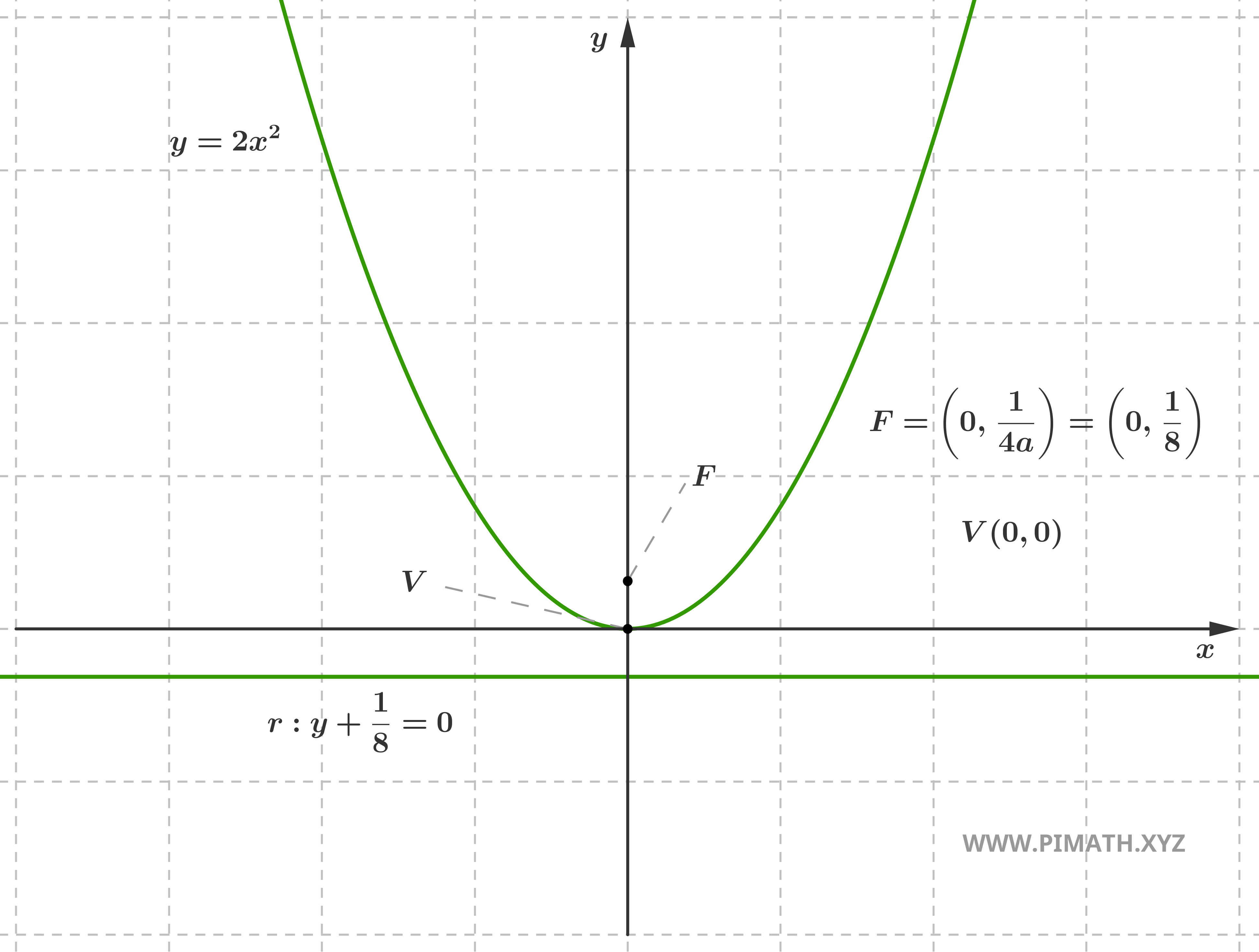
The characteristic elements are: the Vertex: \( V(0, 0) \), the Focus \( F\left(0, \displaystyle \frac{1}{4a}\right) \), the Directrix: \( y = -\displaystyle\frac{1}{4a} \), the Axis of symmetry: \( x = 0 \) (\( y \)-axis) and the Concavity: upward if \( a > 0 \), downward if \( a < 0 \)

Example: Consider the parabola \( y = 2x^2 \). Here \( a = 2 \), so \( p = \displaystyle \frac{1}{4a} = \displaystyle \frac{1}{8} \). The vertex is \( V(0, 0) \), the focus is located at \( F\left(0, \displaystyle \frac{1}{8}\right) \) and the directrix has equation \( y = -\displaystyle \frac{1}{8} \). Since \( a > 0 \), the parabola has upward concavity.

Parabola with Horizontal Axis

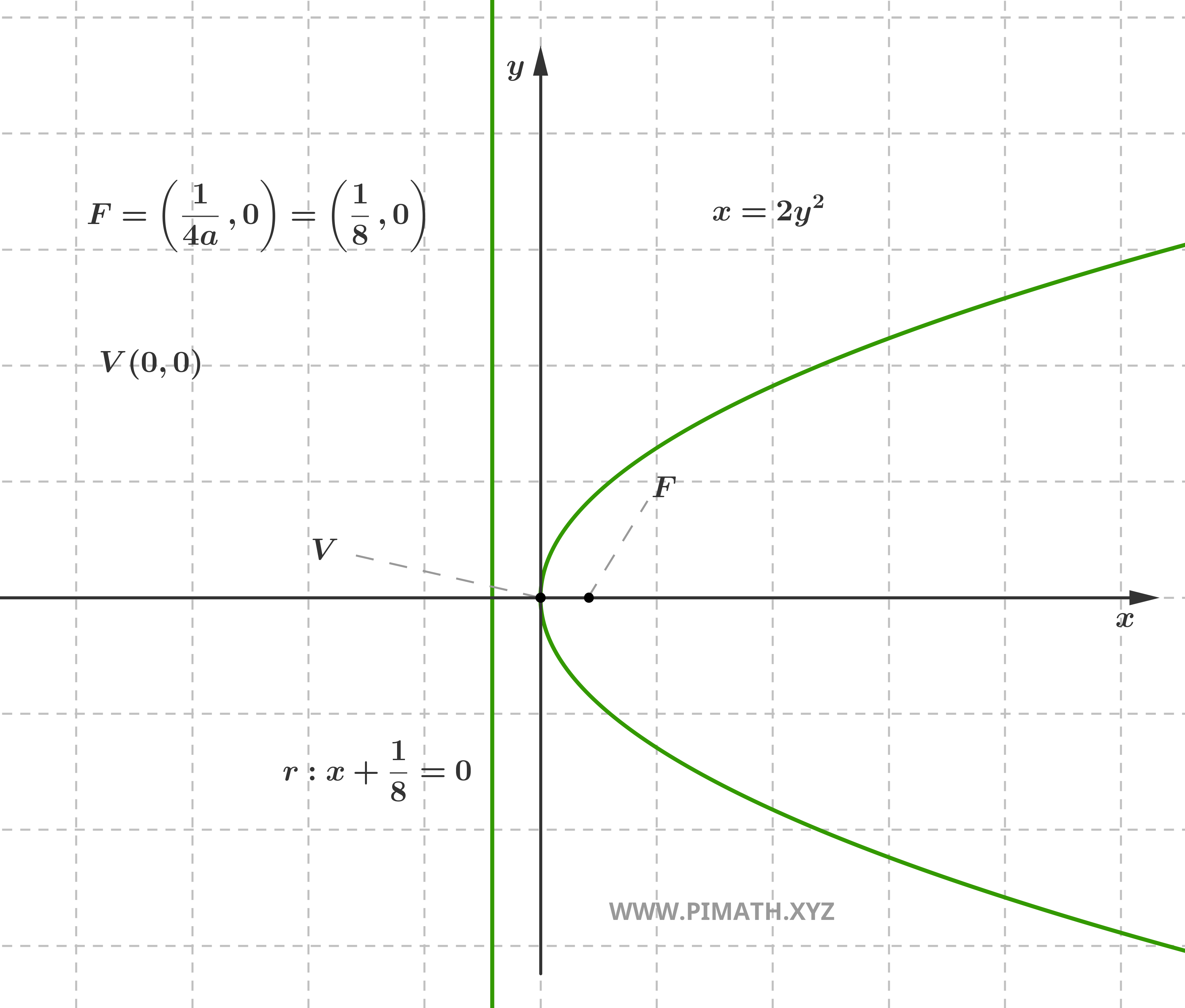
For a parabola with horizontal axis of symmetry, parallel to the abscissa axis, the canonical equation becomes \( x = ay^2 \) (if we take the focus at \( (p, 0)\)), or, equivalently, \( y^2 = 4px \). Also in this case, \( a = \displaystyle \frac{1}{4p} \) is the leading coefficient and \( p \) represents the focal parameter.

Characteristic elements: the Vertex: \( V(0, 0) \), the Focus: \( F\left(\displaystyle \frac{1}{4a}, 0\right) \), the Directrix: \( x = -\displaystyle \frac{1}{4a} \) the Axis of symmetry: \( y = 0 \) (\( x \)-axis), and the Concavity: rightward if \( a > 0 \), leftward if \( a < 0 \).

Example: Consider the parabola \( x = \displaystyle 2y^2 \). Here \( a = 2 \), so \( p = \displaystyle \frac{1}{4a} = \frac{1}{8} \). The vertex is \( V(0, 0) \), the focus is located at \( F\left(\displaystyle \frac{1}{8}, 0\right) \) and the directrix has equation \( x = -\displaystyle \frac{1}{8} \). Since \( a > 0 \), the parabola has rightward concavity.

Relationship between Parameters

It is fundamental to understand the relationship that connects the coefficient \( a \) to the focal parameter \( p \), expressed by the formula \( a = \displaystyle \frac{1}{4p} \), which is equivalent to \( p = \displaystyle \frac{1}{4a} \). This relationship allows us to easily convert from one form to the other of the canonical equation and to immediately determine the geometric characteristics of the parabola once one of the two parameters is known.

Regardless of the orientation of the axis of symmetry, each point \( P(x, y) \) belonging to the parabola always respects the characteristic property that geometrically defines this conic: the distance from the point to the focus is always equal to the distance from the point to the directrix.

A translated parabola is obtained by performing a transformation of the Cartesian plane (translation). This type of geometric transformation keeps the shape of the parabola unchanged, modifying only its position, and represents one of the most important tools for describing parabolas with vertex at arbitrary points in the plane.

Translation Transformation

Translation is a geometric transformation that moves each point of the plane by a constant vector \( \vec{v} = (h, k) \). If we apply a translation by vector \( (h, k) \) to the canonical parabola \( y = ax^2 \), we obtain a new parabola whose vertex moves from the origin to the point \( V(h, k) \).

Equation of the Translated Parabola with Vertical Axis

Starting from the canonical parabola \( y = ax^2 \) with vertex at the origin, a translation by vector \( (h, k) \) produces the translated parabola with equation:

\[ y = a(x - h)^2 + k \]

This is the vertex form of the parabolic equation. The parameter \( a \) maintains its original meaning and determines the opening and orientation of the parabola, while \( h \) and \( k \) represent respectively the horizontal and vertical translation of the vertex.

Expanding the expression \( (x - h)^2 = x^2 - 2hx + h^2 \), we obtain the expanded form:

\[ y = ax^2 - 2ahx + ah^2 + k \]

Setting \( b = -2ah \) and \( c = ah^2 + k \), we find the general form \( y = ax^2 + bx + c \). From this relationship we can deduce that \( h = -\displaystyle \frac{b}{2a} \) and \( k = c - ah^2 = c - \displaystyle \frac{b^2}{4a} \).

Geometric Elements of the Translated Parabola

For a translated parabola \( y = a(x - h)^2 + k \), all characteristic geometric elements undergo the same translation applied to the canonical parabola: the Vertex: \( V(h, k) \), the Axis of symmetry: \( x = h \), the Focus: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \) and the Directrix: \( y = k - \displaystyle \frac{1}{4a} \).

The distance between focus and directrix remains invariant and equal to \( 2p = \displaystyle \frac{1}{2|a|} \), as well as all metric properties of the parabola.

Example of Translated Parabola

Consider the parabola \( y = 2(x - 3)^2 - 5 \). This is a parabola obtained by translating the canonical parabola \( y = 2x^2 \) by \( 3 \) units to the right and \( 5 \) units downward.

The vertex is located at point \( V(3, -5) \), the axis of symmetry has equation \( x = 3 \). The focal parameter is \( p = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \).

The characteristic geometric elements of a parabola are the vertex, the focus and the directrix. These three elements are connected to each other and completely determine the shape and position of the parabola in the Cartesian plane.

The Vertex of the Parabola

Definition. The vertex is the point of the parabola that realizes the absolute extremum (maximum or minimum, depending on the sign of \( a \)) of the quadratic function \( f(x) = ax^2 + bx + c \).

The coordinates of the vertex are:

\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]

where \( \Delta = b^2 - 4ac \) is the discriminant.

Proof. We transform the equation \( y = ax^2 + bx + c \) into canonical form by completing the square:

\[ y = a\left(x^2 + \frac{b}{a}x\right) + c \]

\[ y = a\left(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2\right) + c \]

\[ y = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a} \]

From the canonical form \( y = a(x - h)^2 + k \) we read the vertex \( V(h, k) \), therefore

\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]

Properties of the vertex:

• It lies on the axis of symmetry \( x = -\displaystyle \frac{b}{2a} \)
• It is a minimum point if \( a > 0 \), a maximum point if \( a < 0 \)
• It is the point of the parabola closest to the directrix

The Focus of the Parabola

Definition. The focus is the fixed point such that each point of the parabola is equidistant from the focus and the directrix.

Coordinates of the focus:

\[ F\left(-\frac{b}{2a}, -\frac{\Delta}{4a} + \frac{1}{4a}\right) \]

Proof. In the translated canonical form \( Y = aX^2 \) (with \( X = x + \displaystyle \frac{b}{2a} \), \( Y = y + \displaystyle \frac{\Delta}{4a} \)), the focus is located at \( \left(0, \displaystyle \frac{1}{4a}\right) \).

To verify this, consider a point \( P(X_0, aX_0^2) \) on the parabola. The distance from the candidate focus \( F\left(0, \displaystyle \frac{1}{4a}\right) \) is:

\[ d(P,F) = \sqrt{X_0^2 + \left(aX_0^2 - \frac{1}{4a}\right)^2} \]

The distance from the candidate directrix \( Y = -\displaystyle \frac{1}{4a} \) is:

\[ d(P,d) = \left|aX_0^2 + \frac{1}{4a}\right| \]

For \( a > 0 \), by squaring and simplifying, we verify that \( d(P,F) = d(P,d) \) for each point \( P \) of the parabola.

Returning to the original system, we obtain the indicated coordinates.

Focal parameter: The distance from the vertex to the focus is \( p = \displaystyle \frac{1}{4|a|} \).

The Directrix of the Parabola

Definition. The directrix is the fixed line such that each point of the parabola is equidistant from the directrix and the focus.

Equation of the directrix:

\[ y = -\frac{\Delta}{4a} - \frac{1}{4a} \]

Proof. From the verification of equidistance for the canonical form, the directrix has equation \( Y = -\displaystyle \frac{1}{4a} \) in the translated system. Returning to the original system: \( y = Y - \displaystyle \frac{\Delta}{4a} = -\displaystyle \frac{1}{4a} - \displaystyle \frac{\Delta}{4a} \).

Properties of the directrix:

• It is perpendicular to the axis of symmetry
• It is located at distance \( p = \displaystyle \frac{1}{4|a|} \) from the vertex, opposite to the focus
• The focus-directrix distance is \( 2p = \displaystyle \frac{1}{2|a|} \)

The Axis of Symmetry

The axis of symmetry is the line that passes through the vertex and the focus, with respect to which the parabola is perfectly symmetric. For a parabola with vertical axis and equation \( y = ax^2 + bx + c \), the axis of symmetry has equation \( x = -\displaystyle \frac{b}{2a} \).

Each point of the parabola has a symmetric point with respect to the axis of symmetry. If \( P(x_0, y_0) \) belongs to the parabola, then the point \( P'(2x_V - x_0, y_0) \) also belongs to the parabola, where \( x_V \) is the abscissa of the vertex.

Relationships between Elements

Coordinate system: The three elements form a system with precise relationships:

1. Vertex and focus lie on the axis of symmetry \( x = -\displaystyle \frac{b}{2a} \)
2. The directrix is perpendicular to the axis of symmetry
3. The vertex is equidistant from focus and directrix (distance = focal parameter \( p \))
4. If \( a > 0 \): focus above the vertex, directrix below
5. If \( a < 0 \): focus below the vertex, directrix above

Complete Example

Consider the parabola with equation \( y = 2x^2 - 8x + 3 \). Let us determine all characteristic elements.

First, we identify the coefficients: \( a = 2 \), \( b = -8 \), \( c = 3 \). The discriminant is \( \Delta = b^2 - 4ac = 64 - 24 = 40 \).

The vertex has coordinates \( V\left(-\displaystyle \frac{(-8)}{2 \cdot 2}, -\displaystyle \frac{40}{4 \cdot 2}\right) = V(2, -5) \).

The axis of symmetry has equation \( x = 2 \).

Since \( a = 2 \), the focal parameter is \( p = \displaystyle \frac{1}{4|a|} = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \). Since \( a > 0 \), the parabola has upward concavity, so the focus is located above the vertex: \( F\left(2, -5 + \displaystyle \frac{1}{8}\right) = F\left(2, -\displaystyle \frac{39}{8}\right) \).

The directrix is located below the vertex at distance \( p \): \( y = -5 - \displaystyle \frac{1}{8} = -\displaystyle \frac{41}{8} \).

Special Forms

Canonical form \( y = ax^2 \):

• Vertex: \( V(0, 0) \)
• Focus: \( F\left(0, \displaystyle \frac{1}{4a}\right) \)
• Directrix: \( y = -\displaystyle \frac{1}{4a} \)

Translated form \( y = a(x - h)^2 + k \):

• Vertex: \( V(h, k) \)
• Focus: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \)
• Directrix: \( y = k - \displaystyle \frac{1}{4a} \)

When the vertex of the parabola and another point belonging to the curve are known, it is possible to uniquely determine the equation of the parabola. This method is particularly useful in practical applications where the minimum or maximum point of a quadratic function and a specific value assumed by the function are known.

General Form with Assigned Vertex

Given a parabola with vertex \( V(h, k) \), the most convenient equation to use is the vertex form, which for a parabola with vertical axis is written as \( y = a(x - h)^2 + k \), where \( a \) is the parameter to be determined that controls the opening and orientation of the parabola.

Procedure for Parabolas with Vertical Axis

Let \( V(h, k) \) be the vertex of the parabola and let \( P(x_0, y_0) \) be a point belonging to the parabola with \( x_0 \neq h \). Substituting the coordinates of point \( P \) into the equation \( y = a(x - h)^2 + k \), we obtain:

\[ y_0 = a(x_0 - h)^2 + k \]

From this equation we can directly derive the value of parameter \( a \):

\[ a = \frac{y_0 - k}{(x_0 - h)^2} \]

Once \( a \) is determined, the complete equation of the parabola becomes \( y = \displaystyle \frac{y_0 - k}{(x_0 - h)^2}(x - h)^2 + k \).

Numerical Example - Vertical Axis

Let us determine the equation of the parabola with vertex \( V(3, -2) \) and passing through point \( P(5, 6) \).

We use the vertex form \( y = a(x - 3)^2 - 2 \) and substitute the coordinates of point \( P(5, 6) \):

\[ 6 = a(5 - 3)^2 - 2 \]

\[ 6 = a \cdot 4 - 2 \]

\[ 8 = 4a \]

\[ a = 2 \]

The equation of the parabola is therefore \( y = 2(x - 3)^2 - 2 \). Expanding this expression we obtain \( y = 2(x^2 - 6x + 9) - 2 = 2x^2 - 12x + 18 - 2 = 2x^2 - 12x + 16 \).

To verify correctness, we check that the vertex is indeed \( V(3, -2) \). The abscissa of the vertex is \( x_V = -\displaystyle \frac{b}{2a} = -\displaystyle \frac{-12}{2 \cdot 2} = 3 \) and the ordinate is \( y_V = 2 \cdot 3^2 - 12 \cdot 3 + 16 = 18 - 36 + 16 = -2 \).

Procedure for Parabolas with Horizontal Axis

For parabolas with horizontal axis, the equation in vertex form becomes \( x = a(y - k)^2 + h \), where \( V(h, k) \) is the vertex. Given a point \( P(x_0, y_0) \) belonging to the parabola with \( y_0 \neq k \), the parameter \( a \) is determined by:

\[ a = \frac{x_0 - h}{(y_0 - k)^2} \]

Relationship with the Focal Parameter

Once the coefficient \( a \) is determined, it is possible to calculate all other characteristic elements of the parabola. The focal parameter is \( p = \displaystyle \frac{1}{4|a|} \), the distance from the vertex to the focus. The focus is located at point \( F(h, k + p) \) for parabolas with vertical axis and \( a > 0 \), while it is located at \( F(h, k - p) \) if \( a < 0 \).

Exercise 1. Given the parabola with equation \( y = 3x^2 - 12x + 7 \), determine vertex, focus, directrix and focal parameter.

Solution. From the general form \( y = ax^2 + bx + c \) we identify the coefficients \( a = 3 \), \( b = -12 \), \( c = 7 \).

The vertex is given by the formula \[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \] where \( \Delta = b^2 - 4ac = (-12)^2 - 4(3)(7) = 144 - 84 = 60 \). Substituting:

\[ V\left(-\frac{-12}{2 \cdot 3}, -\frac{60}{4 \cdot 3}\right) = V\left(2, -5\right) \]

The focal parameter is \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 3} = \frac{1}{12} \]

Since \( a = 3 > 0 \), the parabola has upward concavity and the focus is located above the vertex:

\[ F\left(2, -5 + \frac{1}{12}\right) = F\left(2, -\frac{59}{12}\right) \]

The directrix is positioned below the vertex at the same distance as the focus:

\[ y = -5 - \frac{1}{12} = -\frac{61}{12} \]

Exercise 2. Determine the equation of the parabola with vertical axis that has vertex \( V(-1, 4) \) and passes through point \( P(2, -5) \).

Solution. We use the vertex form \( y = a(x - h)^2 + k \) where \( V(h, k) = (-1, 4) \):

\[ y = a(x - (-1))^2 + 4 = a(x + 1)^2 + 4 \]

To determine parameter \( a \), we substitute the coordinates of point \( P(2, -5) \):

\[ -5 = a(2 + 1)^2 + 4 \]

\[ -5 = 9a + 4 \]

\[ a = \frac{-9}{9} = -1 \]

The equation of the parabola is therefore \( y = -(x + 1)^2 + 4 \).

Expanding the expression we obtain the standard form:

\[ y = -(x^2 + 2x + 1) + 4 = -x^2 - 2x + 3 \]

Exercise 3. Given the parabola with horizontal axis \( x = 2y^2 - 8y + 6 \), determine vertex, focus and directrix.

Solution. To identify the vertex, we complete the square with respect to variable \( y \):

\begin{align} x &= 2(y^2 - 4y) + 6 \\ &= 2(y^2 - 4y + 4 - 4) + 6 \\ &= 2(y - 2)^2 - 8 + 6 \\ &= 2(y - 2)^2 - 2 \end{align}

From the form \( x = a(y - k)^2 + h \) we directly read the vertex \( V(h, k) = V(-2, 2) \).

The focal parameter is \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 2} = \frac{1}{8} \]

Since \( a = 2 > 0 \), the parabola opens to the right and the focus is located to the right of the vertex:

\[ F\left(-2 + \frac{1}{8}, 2\right) = F\left(-\frac{15}{8}, 2\right) \]

The directrix is the vertical line positioned to the left of the vertex:

\[ x = -2 - \frac{1}{8} = -\frac{17}{8} \]

Exercise 4. Given the parabola \( y = -2x^2 + 8x - 5 \), determine the equation of the parabola symmetric with respect to the x-axis. Also calculate the intersection points between the two parabolas.

Solution. The parabola symmetric with respect to the x-axis is obtained by changing the sign of variable \( y \). From the original equation \( y = -2x^2 + 8x - 5 \), the symmetric parabola has equation:

\[ y = 2x^2 - 8x + 5 \]

To find the intersection points, we solve the system formed by the two parabolas:

\[ \begin{cases} y = -2x^2 + 8x - 5 \\ y = 2x^2 - 8x + 5 \end{cases} \]

Equating the two expressions:

\[ -2x^2 + 8x - 5 = 2x^2 - 8x + 5 \]

\[ -4x^2 + 16x - 10 = 0 \]

\[ -2(2x^2 - 8x + 5) = 0 \]

\[ 2x^2 - 8x + 5 = 0 \]

Applying the quadratic formula:

\[ x = \frac{8 \pm \sqrt{64 - 40}}{4} = \frac{8 \pm \sqrt{24}}{4} = \frac{8 \pm 2\sqrt{6}}{4} = \frac{4 \pm \sqrt{6}}{2} \]

The corresponding ordinates are calculated by substituting into one of the two equations:

For \( x_1 = \displaystyle \frac{4 + \sqrt{6}}{2} \) : \( y_1 = 2\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)

For \( x_2 = \displaystyle \frac{4 - \sqrt{6}}{2} \) : \( y_2 = 2\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)

The intersection points are:

\[ A\left(\frac{4 + \sqrt{6}}{2}, -\frac{1}{2}\right) \quad \text{and} \quad B\left(\frac{4 - \sqrt{6}}{2}, -\frac{1}{2}\right) \]

Since both points have the same ordinate, the distance between them is simply:

\[ d(A,B) = \left|\frac{4 + \sqrt{6}}{2} - \frac{4 - \sqrt{6}}{2}\right| = \left|\frac{2\sqrt{6}}{2}\right| = \sqrt{6} \]

Exercise 5. Determine the equation of the parabola with vertical axis that has focus \( F(1, 5) \) and directrix \( y = 3 \). Verify whether point \( P(3, 6) \) belongs to the parabola.

Solution. The vertex of the parabola is the point equidistant from the focus and the directrix, located on the line perpendicular to the directrix and passing through the focus. Since the directrix is horizontal, the vertex has the same abscissa as the focus and ordinate equal to the arithmetic mean:

\[ V\left(1, \frac{5 + 3}{2}\right) = V(1, 4) \]

The focal parameter is the distance from the vertex to the focus:

\[ p = |5 - 4| = 1 \]

The coefficient of the parabola is therefore:

\[ a = \frac{1}{4p} = \frac{1}{4 \cdot 1} = \frac{1}{4} \]

The equation of the parabola in vertex form is:

\[ y = \frac{1}{4}(x - 1)^2 + 4 \]

To verify whether \( P(3, 6) \) belongs to the parabola, we substitute its coordinates:

\[ y = \frac{1}{4}(3 - 1)^2 + 4 = \frac{1}{4} \cdot 4 + 4 = 1 + 4 = 5 \neq 6 \]

We confirm the result using the geometric definition of the parabola. The distance from P to the focus is:

\[ d(P,F) = \sqrt{(3-1)^2 + (6-5)^2} = \sqrt{4 + 1} = \sqrt{5} \]

The distance from P to the directrix is:

\[ d(P, \text{directrix}) = |6 - 3| = 3 \]

Since \( \sqrt{5} \neq 3 \), point \( P(3, 6) \) does not belong to the parabola.