Even and odd functions are distinguished by their symmetries with respect to the y-axis and the origin, respectively.
Definition. A function $ f : X \to Y $ is called even if, for every $ x \in X $
$$ f(-x) = f(x) $$
Example. The function $ f(x) = \cos x $ is an even function. Indeed, for every $ x \in \mathbb{R} $, it holds that $ \cos(-x) = \cos x $.
Example. The function $ f(x) = x^2 $ is an even function. Indeed, for every $ x \in \mathbb{R} $, we have $ (-x)^2 = x^2 $. Its Cartesian graph is a parabola, as shown in the figure:
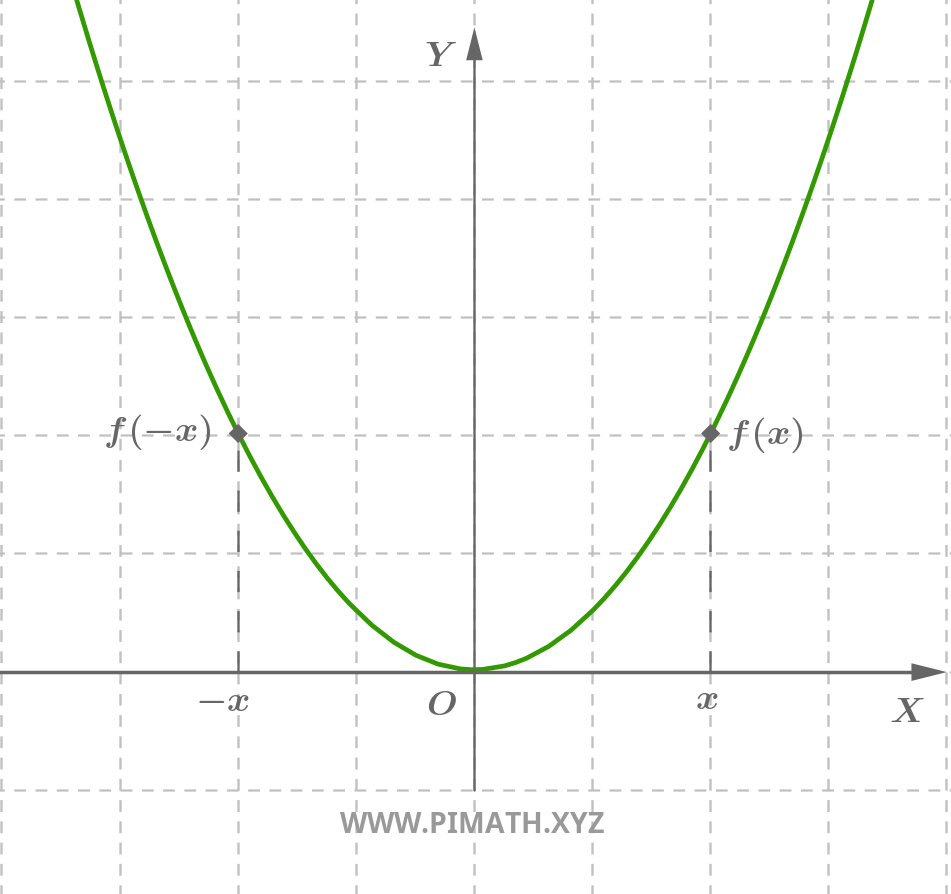
A function is odd if, given $ x $ as a point in the domain, the image of $ - x $ is exactly the image of the point $ x $ with the sign changed.
Definition. A function $ f : X \to Y $ is called odd if, for every $ x \in X $
$$ f(-x) = -f(x) $$
Definition. The function $ f(x) = \sin x $ is an odd function. Indeed, for every $ x \in \mathbb{R} $, it holds that $ \sin(-x) = -\sin x $.
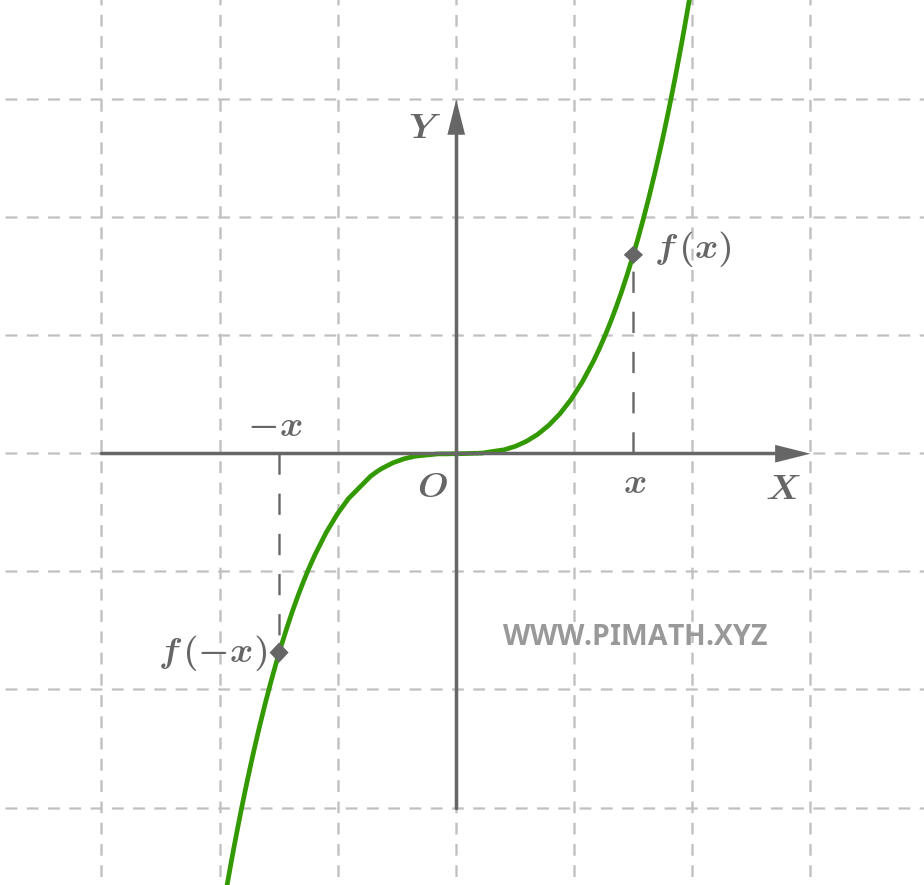
Example. The function $ f(x) = x^3 $ is an odd function. Indeed, for every $ x \in \mathbb{R} $, we have $ (-x)^3 = -x^3 $. Its Cartesian graph is shown in the figure:
As mentioned earlier, an even function is symmetric with respect to the y-axis; this means that if we need to study the graph of an even function, we only need to analyze it for positive (or negative) values, as it will be symmetric about the y-axis. The same applies to an odd function, provided that the graph is traced symmetrically with respect to the origin of the coordinate axes. Another scenario in which even and odd functions are particularly useful is when we need to calculate the integral over a symmetric interval with respect to the origin. If $ f $ is even, we have
$$ \int_{-a}^{a} f(x) dx = 2 \int_{0}^{a} f(x) dx $$
If instead $ f $ is odd, we have
$$ \int_{-a}^{a} f(x) dx = 0 $$
If $ f : X \to Y $ satisfies that $ f(-x) \neq f(x) $ and $ f(-x) \neq -f(x) $, then it is neither even nor odd.
Example. The function $ f(x) = e^x $ is neither even nor odd, nor is the function $ f(x) = x + 1 $.

