First-Degree Equations

A first-degree equation is a first-degree polynomial set equal to zero. Generally, an equation is first-degree if it can be written in standard form:

\[ ax + b = 0 \quad \text{with} \quad a \neq 0 \]

The part to the left of the equals sign is called the left-hand side, while the part to the right is called the right-hand side. 

Table of Contents

• How to solve a first-degree equation
• First principle of equivalence
• Second principle of equivalence
• Worked Examples
• Common mistakes to avoid
• Geometric Meaning

Solving a first-degree equation means finding the value that, when substituted for the unknown \( x \), satisfies the equation. This is equivalent to saying that the value (solution of the equation) must make the equality true. The solution process involves certain steps, called principles of equivalence for equations.

The first principle of equivalence states that by adding or subtracting the same quantity or algebraic expression to both sides of an equation, the solution set does not change.

Thanks to this principle, we can subtract the quantity \( -b \) from both sides:

\[ ax = -b \]

Note that adding or subtracting a quantity to both sides is equivalent to "moving" it from one side to the other, provided the sign is changed. For now, we have moved \( b \) to the right-hand side with its sign changed, thus \( -b \).

The second principle of equivalence states that by multiplying or dividing both sides by the same non-zero number, the solution set of the equation does not change. 

Applying this principle to the equivalent equation \( ax = -b \), then dividing both sides by the number \( a \neq 0 \), we obtain:

\[ x = -\frac{b}{a} \]

It is important to emphasize that \( a \) must be different from zero for the equation to make sense. Indeed, if \( a = 0 \) the equation would become \( 0 \cdot x + b = 0 \) and thus \( b = 0 \), which does not represent an equation in \( x \) and would be impossible if \( b \neq 0 \).

From now on, the goal will be to isolate the variable \( x \) on the left-hand side, or on the right (it makes no difference).

Example 1. Solve the equation \( 3x - 1 = 0\).

Solution. We move \( -1 \) to the right-hand side (changing its sign):

\[ 3x = 1 \]

Finally, dividing both sides by \( 3 \) we obtain the desired solution:

\[ x = \frac{1}{3} \]

Check. To verify that this is the correct solution, we substitute the value found into the original equation. We get:

\[ 3 \cdot \frac{1}{3} - 1 = 1 - 1 = 0 \]

Therefore, the solution is correct.

Example 2: Solve the first-degree equation \(\displaystyle\frac{1}{2}(x-1)=-x+1\).

Solution. We start by isolating the unknown \( x \) on the left-hand side:

\[ \frac{1}{2}(x - 1) = -x + 1 \implies \frac{x}{2} - \frac{1}{2} = -x + 1 \]

Now we add \(x\) to both sides of the equation:

\[ \frac{x}{2} + x - \frac{1}{2} = 1 \]

We simplify by converting \(x\) to a term with a common denominator:

\[ \frac{x}{2} + \frac{2x}{2} - \frac{1}{2} = 1 \implies \frac{3x}{2} - \frac{1}{2} = 1 \]

We add \(\displaystyle\frac{1}{2}\) to both sides:

\[ \frac{3x}{2} = \frac{3}{2} \]

Now we multiply both sides by \(\displaystyle\frac{2}{3}\) to solve for \(x\):

\[ x = 1 \]

Therefore, the solution is \( x = 1 \).

Check. As before, we substitute \( x = 1 \) into the original equation:

\[ \frac{1}{2}(x - 1) = -x + 1 \]

When \( x = 1 \), we get:

\[ \frac{1}{2}(1 - 1) = -1 + 1 \]

We calculate both sides:

\[ \frac{1}{2} \cdot 0 = 0 \quad \text{and} \quad -1 + 1 = 0 \]

Both sides are equal, so the solution is correct.

Example 3. Solve the equation \( 5(x - 2) - 3(2x + 1) = 7 - 4x \)

Solution. We apply the distributive property:

\[ 5x - 10 - 6x - 3 = 7 - 4x \]

\[ -x - 13 = 7 - 4x \]

We move the terms with \(x\) to the left-hand side and the constant terms to the right-hand side:

\[ -x + 4x = 7 + 13 \]

\[ 3x = 20 \]

We divide both sides by 3:

\[ x = \frac{20}{3} \]

Check. We substitute \(\displaystyle x = \frac{20}{3}\) into the original equation:

\[ 5\left(\frac{20}{3} - 2\right) - 3\left(2\cdot\frac{20}{3} + 1\right) = 7 - 4\cdot\frac{20}{3} \]

We calculate the left-hand side:

\[ 5\left(\frac{20}{3} - \frac{6}{3}\right) - 3\left(\frac{40}{3} + \frac{3}{3}\right) = 5\cdot\frac{14}{3} - 3\cdot\frac{43}{3} = \frac{70}{3} - \frac{129}{3} = -\frac{59}{3} \]

We calculate the right-hand side:

\[ 7 - 4\cdot\frac{20}{3} = \frac{21}{3} - \frac{80}{3} = -\frac{59}{3} \]

Both sides are equal, so the solution is verified:

\[ x = \frac{20}{3} \]

When solving first-degree equations, it is important to be careful about some frequent errors:

Sign error when moving terms: When moving a term from one side to the other, remember to change its sign. For example, in the equation \(2x + 3 = 5\), moving the \( 3 \) gives \(2x = 5 - 3\) and not \(2x = 5 + 3\).

Incomplete distribution: When you have an expression like \(3(x + 2)\), the coefficient \( 3 \) must be multiplied by all terms inside the parentheses. A common error is writing \(3x + 2\) instead of the correct \(3x + 6\).

Errors with fractions: When you have an equation like \(\displaystyle \frac{x}{2} = 3\), to isolate \(x\) you must multiply both sides by 2, obtaining \(x = 6\). It is wrong to write \(x = \displaystyle \frac{3}{2}\).

Imprecise simplification: In an equation like \(2x - x = 5\), don't forget to simplify like terms before proceeding. The correct form is \(x = 5\).

Missing verification: Skipping the verification step can lead to not noticing calculation errors. It is always advisable to substitute the solution found into the original equation to confirm that it is correct.

Solving a first-degree equation \( ax + b = 0\) means finding the value at which the line with equation

\[ y = ax + b \]

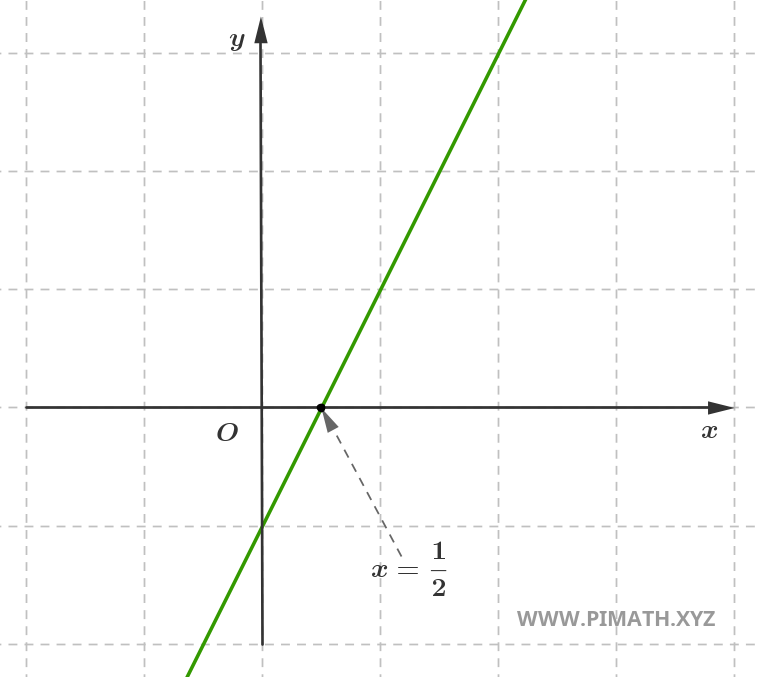
intersects the x-axis. For example, the line with equation \( y = 2x - 1 \)

intersects the x-axis at the point \( x = \displaystyle \frac{1}{2} \), as shown in the figure.

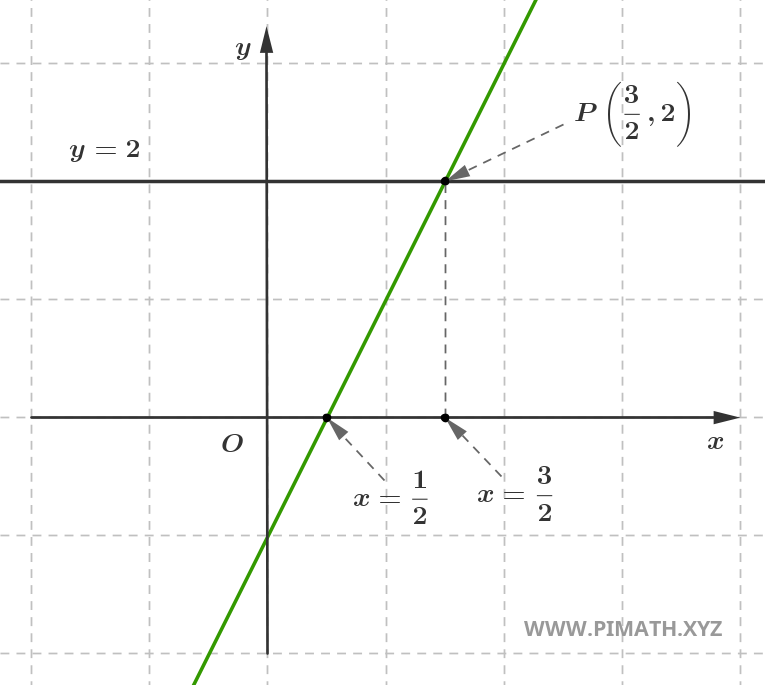
We have said that the solution of a first-degree equation \( ax + b = 0 \) is the x-coordinate where the line intersects the x-axis. Now, let us ask ourselves another question: how can we determine the value of \( x \) for which the line \( y = ax + b \) takes a specific value, for example \( y = 2 \)?

To do this, we simply set \( y = 2 \) in the equation of the line. We thus obtain \( 2 = 2x - 1 \iff 2x - 3 = 0 \), therefore:

\[ x=\frac{3}{2} \]

As shown in the figure, the solution we found corresponds to the y-coordinate \(y=2\).