First Degree Inequalities

A first-degree inequality is an algebraic expression that establishes an order relation between two terms containing a linear variable. It can be written in the form:

\[ a x + b \leq 0 \quad \text{or} \quad a x + b \geq 0 \]

where \( a \) and \( b \) are real coefficients with \( a \neq 0 \) and \( x \) is the unknown variable. It is called a strict inequality if

\[ a x + b < 0 \quad \text{or} \quad a x + b > 0 \]

Table of Contents

• Difference between First-Degree Equations and Inequalities
• Principles of Equivalence for Inequalities
• How to Solve First-Degree Inequalities
• Graphical Representation of Solutions to First-Degree Inequalities

A first-degree equation is an equality between two expressions containing a linear variable. Its solution is a unique value that satisfies the equality. A first-degree inequality, on the other hand, defines a set of values for which the order relation is satisfied. The set of solutions to an inequality is generally an interval of real numbers.

The solution of a first-degree inequality is based on three fundamental principles:

First Principle of Equivalence

The principle of equivalence for inequalities, or the addition principle, states that if the same number is added or subtracted to both sides of an inequality, the order relation does not change. For example:

If \( a x + b \leq 0 \), then we can add \( c \) to both sides and get:

\[ a x + b + c \leq c \]

Second Principle of Equivalence

The second principle of equivalence, states that if both sides of an inequality are multiplied or divided by a positive number, the order relation does not change. However, if both sides are multiplied or divided by a negative number, the inequality must be reversed. Here are some examples:

If \( a x + b \leq 0 \) and we multiply both sides by a positive number \( k \), we get:

\[ k(a x + b) \leq k \cdot 0 \]

If, instead, we multiply by a negative number \( k \), the inequality becomes:

\[ k(a x + b) \geq k \cdot 0 \]

Be Careful When Changing the Sign of the Inequality

When multiplying or dividing both sides of an inequality by a negative number, it is crucial to reverse the sign of the inequality. For example:

If \( -3 x \leq 6 \), dividing both sides by \( -3 \) requires reversing the inequality:

\[ x \geq -2 \]

The solution of a first-degree inequality can be divided into clear and systematic steps. The general steps to solve a first-degree inequality are:

General Steps to Solve an Inequality

• Isolate the term with the variable: Move all terms that do not contain the variable to one side (usually the right-hand side) of the inequality and the terms that contain the variable to the other side.
• Apply the addition or subtraction principle: If necessary, add or subtract the same number from both sides of the inequality to isolate the term with the variable.
• Multiply or divide by a coefficient: If the variable has a numerical coefficient, divide both sides by the coefficient of the variable. If you multiply or divide by a negative number, remember to reverse the inequality sign.
• Verify the solution: Once the variable is isolated, check if the solution satisfies the original inequality.

Practical Examples with Step-by-Step Explanations

Now let's look at a practical example of solving a first-degree inequality:

Example 1. Solve the inequality \( 3x - 5 \leq 7 \).

Let's start by applying the steps described above:

1. Isolate the term with the variable: Add \( 5 \) to both sides to get: \[ 3x \leq 7 + 5 \quad \Rightarrow \quad 3x \leq 12 \]
2. Divide both sides by \( 3 \): Divide both sides by \( 3 \) to isolate \( x \): \[ x \leq \frac{12}{3} \quad \Rightarrow \quad x \leq 4 \]
3. Verify the solution: The solution \( x \leq 4 \) is the final answer. If we substitute \( x = 4 \) into the original inequality, we get: \[ 3(4) - 5 = 12 - 5 = 7 \quad \Rightarrow \quad 7 \leq 7 \] Which is true. So the solution is correct, and the graphical representation is as follows:

Example 2: Solve the inequality \( -2x + 3 > 7 \)

Now let's look at another example with a negative coefficient in front of the variable:

1. Isolate the term with the variable: First, subtract \( 3 \) from both sides: \[ -2x > 7 - 3 \quad \Rightarrow \quad -2x > 4 \]
2. Divide both sides by \( -2 \): When dividing by a negative number, reverse the sign of the inequality: \[ x < \frac{4}{-2} \quad \Rightarrow \quad x < -2 \]
3. Verify the solution: The solution \( x < -2 \) is correct. If we substitute \( x = -3 \) (which is less than -2), we get: \[ -2(-3) + 3 = 6 + 3 = 9 \quad \Rightarrow \quad 9 > 7 \] Which is true. So the solution is correct, and the graphical representation is as follows.

As we have already seen, the graphical representation of the solutions of a first-degree inequality on a number line is a very useful way to visualize the solution interval. In general, the solution to a first-degree inequality can be represented as a segment or a part of the number line, depending on whether the inequality is strict or not.

How to Represent Solutions on a Number Line

To represent the solutions of a first-degree inequality on a number line, follow these steps:

1. Identify the solution: Once the inequality is solved, determine the solution interval. For example, if the solution is \( x \leq 4 \), the solution interval is \( (-\infty, 4] \).
2. Draw the number line: Draw a horizontal line and mark the significant numbers, such as the limits of the solution interval.
3. Indicate the solution:
   • If the inequality is of the type \( \leq \) or \( \geq \), mark the boundary of the interval with a closed circle on the number line.
   • If the inequality is of the type \( < \) or \( > \), mark the boundary with an open circle, indicating that the point is not included in the solution.
4. Indicate the interval: Draw a continuous or dashed line to represent the solution interval.

Graphical Interpretation of the Solution

The graphical interpretation of the solutions of an inequality on a number line allows for a quick visualization of the set of values that satisfy the relationship. Here are some examples of how the solutions are represented:

Example 1. Solution \( x \leq 4 \)

The solution \( x \leq 4 \) means that all numbers less than or equal to \( 4 \) are solutions. The graphical representation is as follows:

Solution. \( x \leq 4 \).

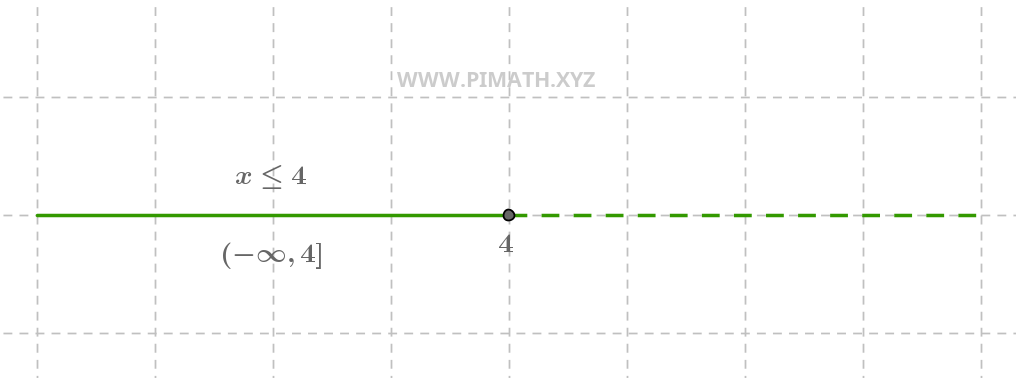
On the number line, we see a closed circle at \( 4 \) (because \( 4 \) is included) and a ray starting from \( -\infty \) going towards \( 4 \).

Example 2. Solution \( x > -2 \).

The solution \( x > -2 \) means that all numbers greater than \( -2 \) are solutions. The graphical representation is as follows:

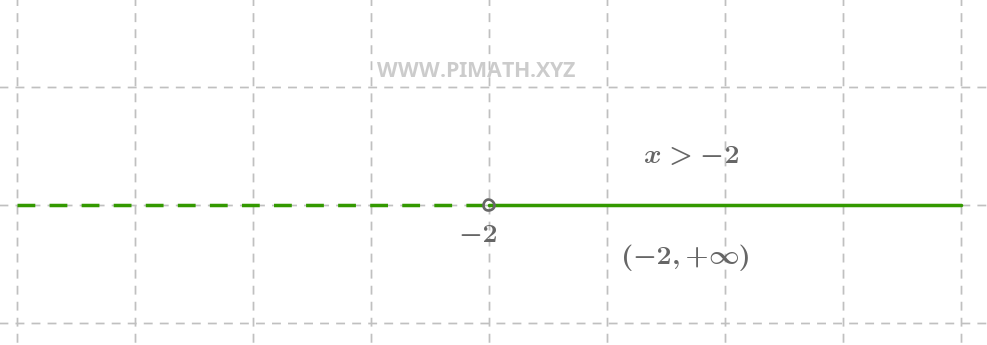
On the number line, we see an open circle at \( -2 \) (because \( -2 \) is not included) and a continuous line going from \( -2 \) to \( +\infty \).

Example 3. Solution \( -2 \leq x < 5 \)

The solution \( -2 \leq x < 5 \) is an interval that includes \( -2 \) but excludes \( 5 \). The graphical representation is as follows:

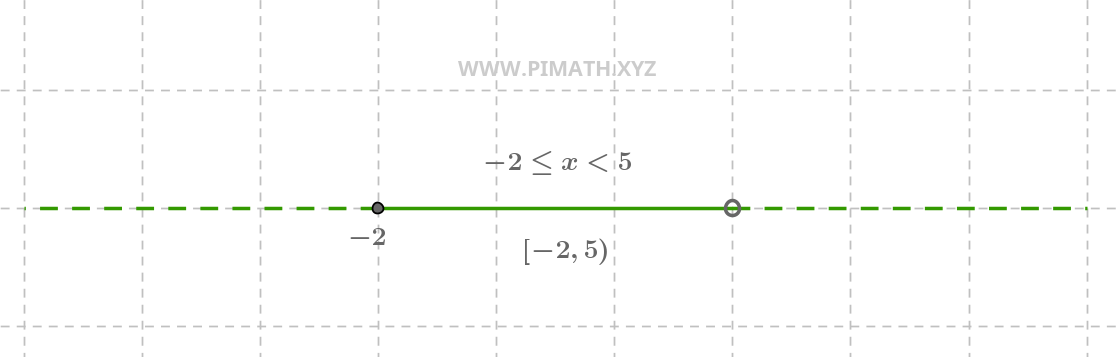
On the number line, we see a closed circle at \( -2 \) and an open circle at \( 5 \), with a continuous line between them.

The graphical interpretation of these solutions visually shows which values satisfy the inequality, making it easy for learners to see the solution set.