A line is a primitive concept in Euclidean geometry, meaning it cannot be defined in more elementary terms but is taken as a fundamental entity. It is intuitively described as an infinite set of points arranged in a constant direction, extending indefinitely in both directions. In a Cartesian coordinate system, a line can be represented by a linear equation and is characterized by a slope that determines its inclination with respect to the x-axis.
Contents
- How to Find the Equation of a Line Through Two Points
- How to Find the Explicit Equation of a Line
- How to Find the Implicit Equation of a Line
- Geometric Meaning of the Slope
- How to Find the Parametric Equation of a Line
- How to Find a Line Perpendicular to a Given Line
- Worked Examples on Lines
How to Find the Equation of a Line Through Two Points
Suppose we know two distinct points in the Cartesian plane: \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \).
The equation of points belonging to the line passing through \( P_1 \) and \( P_2 \) is given by the following formula:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
This can be understood by observing that the triangles \( \triangle P_1P'P \) and \( \triangle P_1P'_2P_2 \) in the figure:
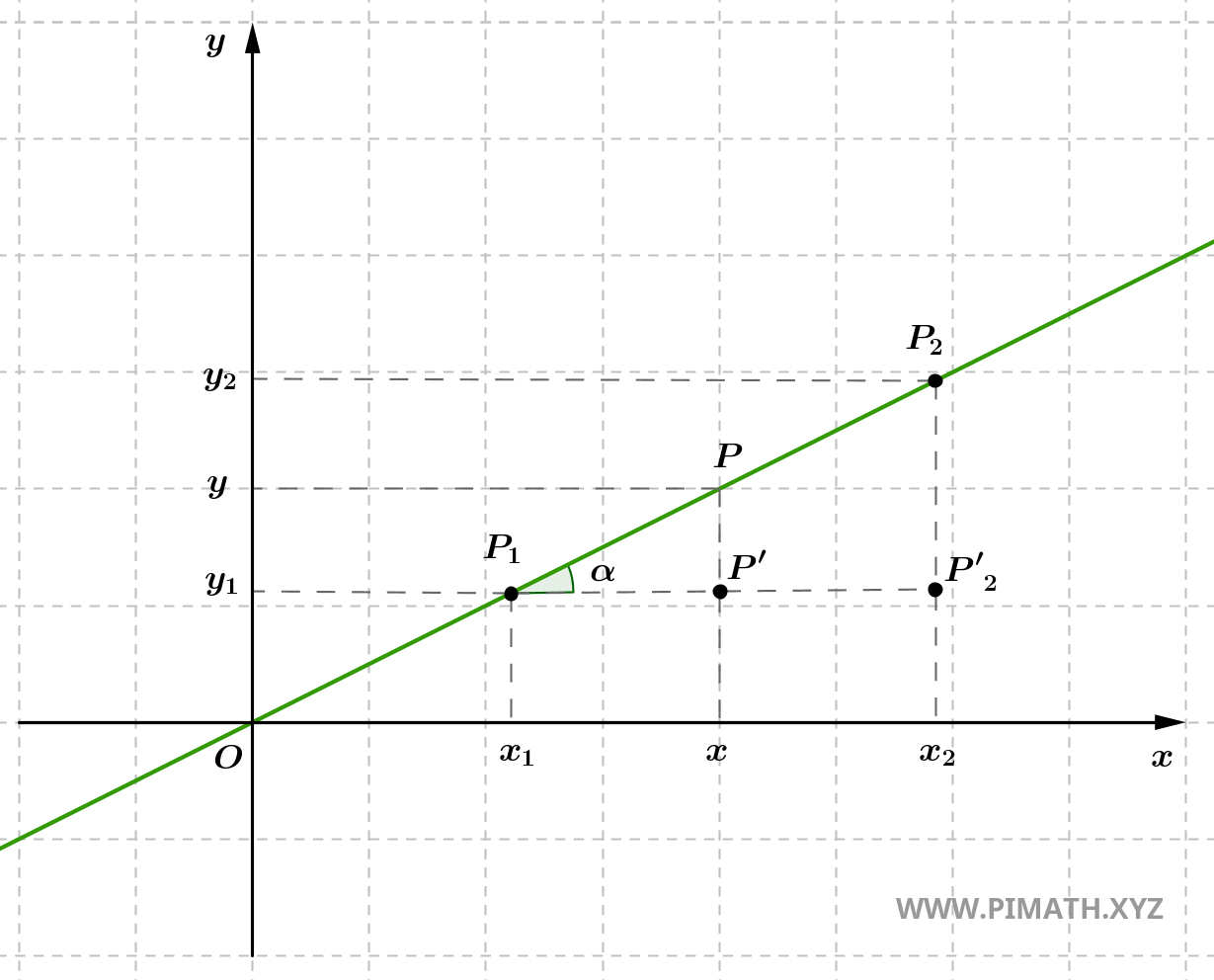
are similar according to the first criterion of similarity, which states that two triangles are similar if they have two corresponding angles that are congruent. In this case, both triangles have a right angle and a congruent acute angle, determined by the inclination of the line with respect to the x-axis. This results in proportionality between corresponding sides.
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
Solving for \( y \), we obtain the explicit form of the line equation:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \]
The acute angle common to both triangles, often denoted as \( \alpha \), represents the angle of inclination of the line with respect to the x-axis. This angle plays a fundamental role in line geometry, as its tangent gives the slope of the line, namely: \[ m = \tan \alpha = \frac{y_2 - y_1}{x_2 - x_1}. \] This relationship allows us to interpret the slope as a measure of the angular inclination of the line in the Cartesian plane.
How to Find the Explicit Equation of a Line
The equation of a line passing through two distinct points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) can be written in explicit form using the so-called point-slope form:
\[ y = y_1 + m(x - x_1) \]
where
\[ m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]
is the slope of the line. This expression allows us to calculate the value of \( y \) corresponding to any given value of \( x \), starting from a known point on the line and its slope.
From this form, we can derive the slope-intercept form of the line equation, which is:
\[ y = mx + b \]
In this equation:
- \( m \) is the slope, which represents the steepness of the line;
- \( b \) is the y-intercept, which is the value of \( y \) at the point where the line intersects the y-axis (i.e., when \( x = 0 \)).
This form is particularly useful because it immediately reveals both the direction of the line (through \( m \)) and its intersection point with the y-axis (through \( b \)). If we know \( m \) and \( b \), we can plot the line without needing additional points.
To convert from point-slope form to slope-intercept form, we simply expand and isolate \( y \). For example:
\[ y = y_1 + m(x - x_1) = mx + (y_1 - mx_1) \]
From which we directly obtain:
\[ y = mx + b \quad \text{where} \quad b = y_1 - mx_1 \]
How to Find the Implicit Equation of a Line
Let's start with the point-slope form of the line equation, passing through two points \( (x_1, y_1) \) and \( (x_2, y_2) \):
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
We multiply both sides by \( x_2 - x_1 \neq 0 \):
\[ (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1) \]
Expanding both sides:
\[ (x_2 - x_1)y - (x_2 - x_1)y_1 = (y_2 - y_1)x - (y_2 - y_1)x_1 \]
Moving all terms to the left side:
\[ (x_2 - x_1)y - (y_2 - y_1)x + \left( (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \right) = 0 \]
This is the implicit form of the line equation. If we define the coefficients as:
\[ \begin{cases} a = -(y_2 - y_1) \\ b = x_2 - x_1 \\ c = (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \end{cases} \]
the equation takes the general form:
\[ ax + by + c = 0 \]
Alternatively, if we introduce the slope \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \), we can start from the explicit form of the line:
\[ y = m(x - x_1) + y_1 \]
Moving everything to the left side to obtain the implicit form:
\[ y - m x + (m x_1 - y_1) = 0 \]
So the implicit form with slope \( m \) has:
\[ a = -m, \quad b = 1, \quad c = m x_1 - y_1 \]
and the general form:
\[ ax + by + c = 0 \]
The implicit form is useful when studying geometric properties of the line or checking whether a point belongs to the line without having to solve for \( y \).
Geometric Meaning of the Slope
In the context of this equation, the term:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
represents the slope of the line. The slope is a measure of the inclination of the line with respect to the x-axis. If the slope is positive, the line is increasing (rises from left to right); if it is negative, the line is decreasing (falls from left to right).
In other words, the slope describes how quickly the line rises or falls relative to the x-axis. The slope is a crucial parameter for determining the orientation of the line in the Cartesian plane. Depending on the value of the slope, we can make the following observations:
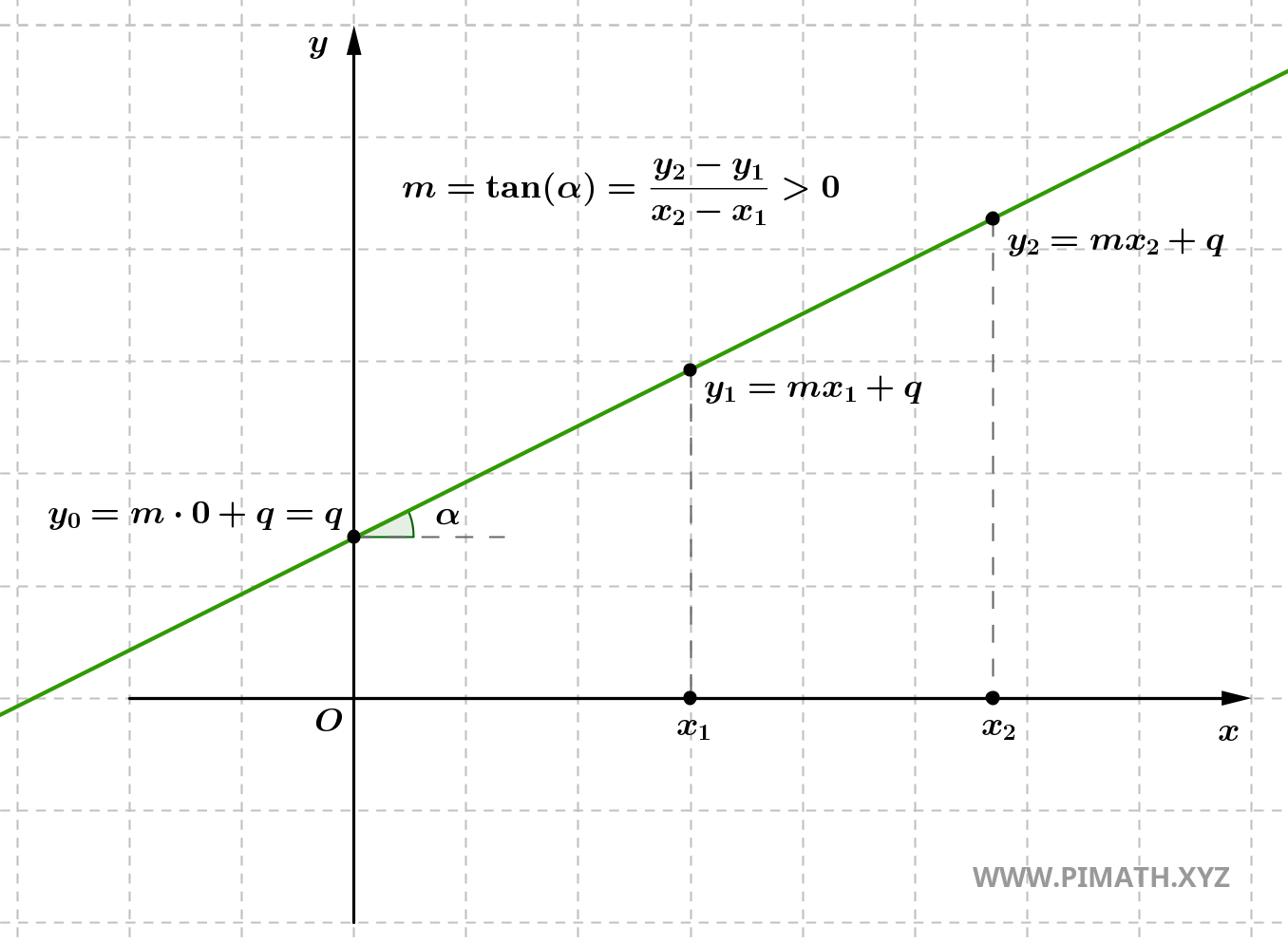
- If \( m > 0 \), the line is increasing, meaning it rises from left to right. This means that for every increase in \( x \), \( y \) also increases. The line forms an acute angle with the x-axis.
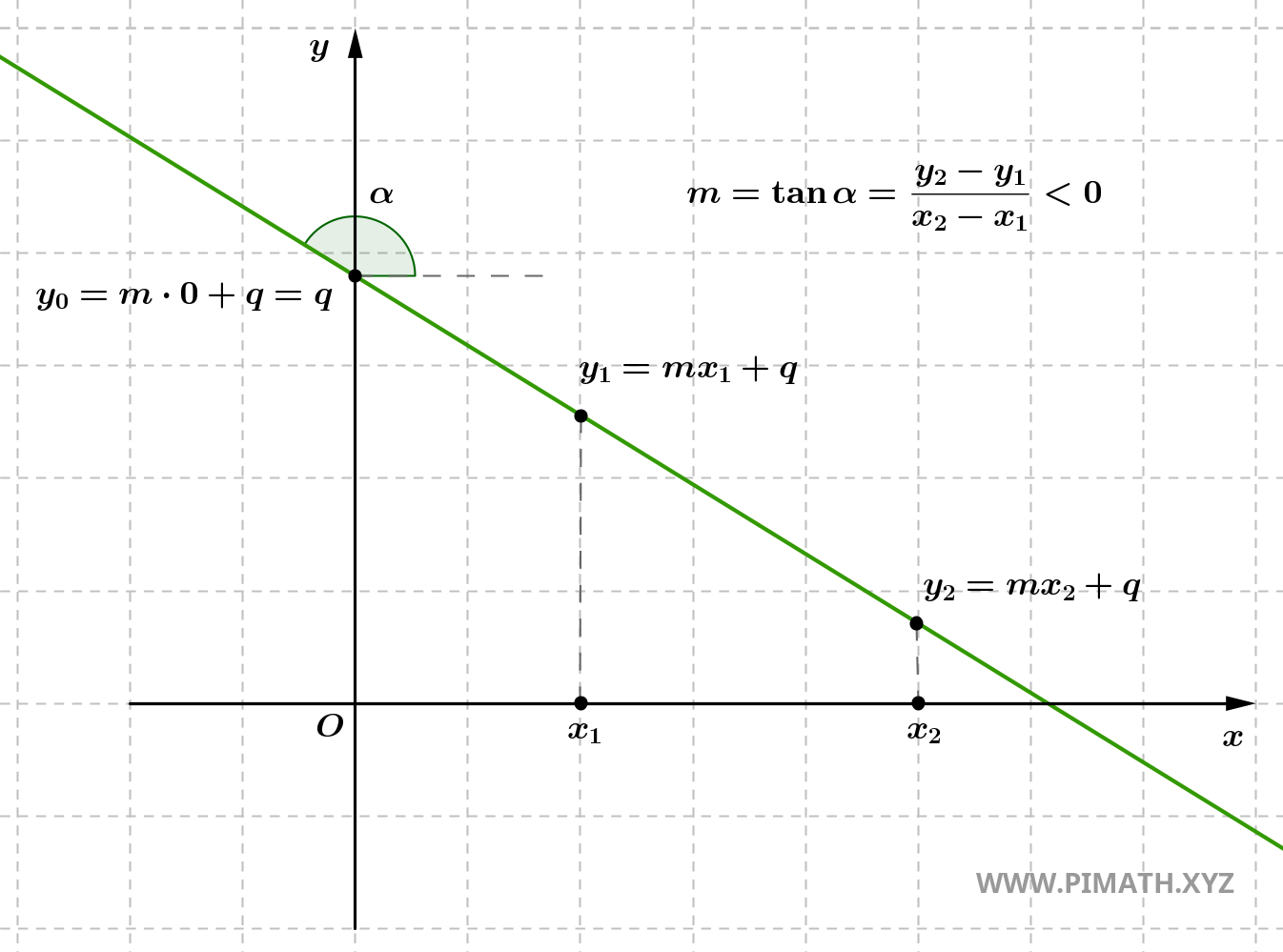
- If \( m < 0 \), the line is decreasing, meaning it falls from left to right. In this case, for every increase in \( x \), the value of \( y \) decreases. The line forms an obtuse angle with the x-axis.
- If \( y_2 = y_1 \), the slope is zero, which means the line is horizontal. In this case, there is no vertical change (the difference between the y-coordinates \( y_2 - y_1 \) is zero). The line is parallel to the x-axis and has no vertical inclination.
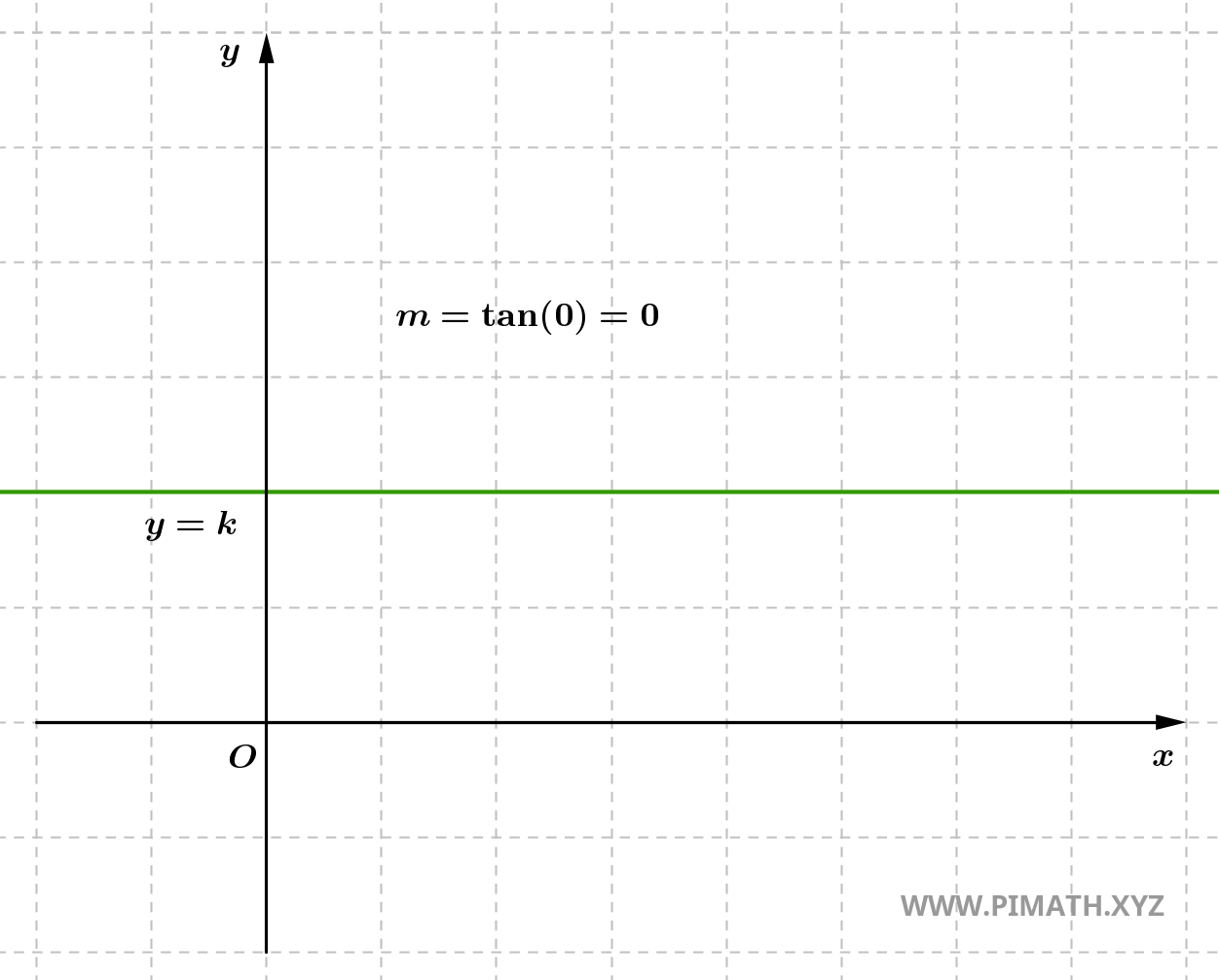
- If \( x_2 = x_1 \), the slope is undefined, which means the line is vertical. In this case, there is no horizontal change (the difference between the x-coordinates \( x_2 - x_1 \) is zero), so a numerical slope cannot be defined. The line is parallel to the y-axis and has no horizontal inclination.
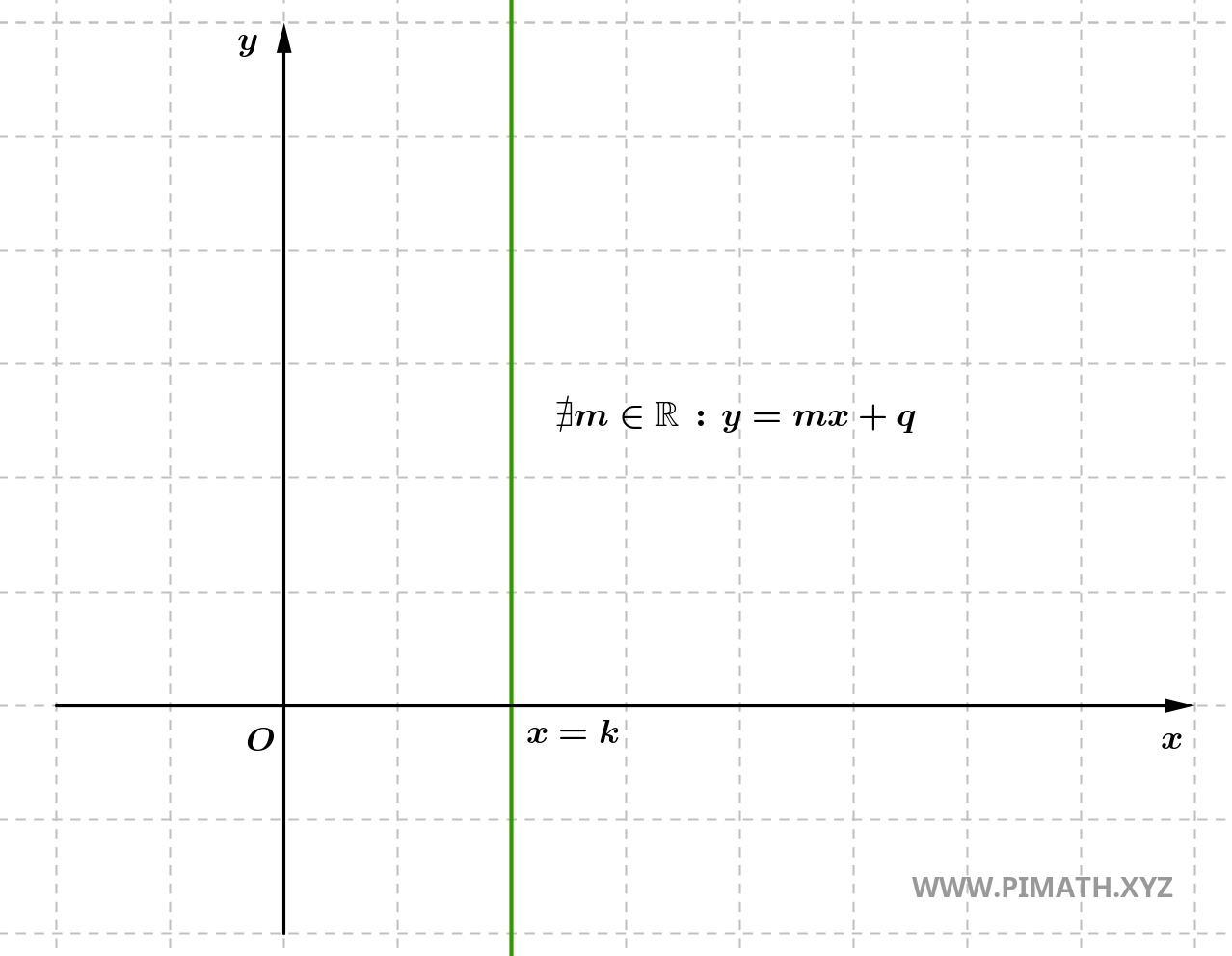
In general, the slope \( m \) provides important information about the behavior of the line. If the line is increasing, the value of \( y \) increases as \( x \) increases; if it is decreasing, the value of \( y \) decreases as \( x \) increases; if the line is vertical, it means that \( y \) does not depend on \( x \) and the line has no horizontal inclination.
How to Find the Parametric Equation of a Line
The line passing through points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) can also be described in parametric form. In this representation, the coordinates \( x \) and \( y \) of a point on the line are expressed as functions of a real parameter \( t \), which varies along the line.
The parametric equation of the line is given by:
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Here, \( t \) is the parameter that can take any real value. As \( t \) varies, the point \( (x, y) \) moves along the line connecting the two points \( P_1 \) and \( P_2 \).
The parametric form therefore represents a family of points on the line, where the parameter \( t \) uniquely defines each point on the line. When \( t = 0 \), we get point \( P_1(x_1, y_1) \); when \( t = 1 \), we get point \( P_2(x_2, y_2) \). Values of \( t \) between 0 and 1 describe points on the line between \( P_1 \) and \( P_2 \), while values of \( t \) greater than 1 or less than 0 extend the line beyond these points.
The parametric formula is based on the concept of a direction vector, which is the vector connecting \( P_1 \) and \( P_2 \). Indeed, the difference \( (x_2 - x_1, y_2 - y_1) \) is the direction vector of the line, and the parameter \( t \) is the scaling factor that allows movement along the line.
The parametric form is particularly useful in various areas of analytic geometry, such as in the study of curves in general.
How to Find a Line Perpendicular to a Given Line
When two lines are perpendicular, their slopes are related by a specific relationship. If one line has slope \( m \), the slope of the line perpendicular to it is given by:
\[ m_\perp = -\frac{1}{m}. \]
This formula expresses the fact that the product of the slopes of two perpendicular lines equals \(-1\). The reason for this relationship can be seen in the fact that the angles formed by the two lines must be 90° (a right angle), and therefore the tangent of the angle between the lines must satisfy this condition.
To find the equation of the perpendicular line passing through a point \( (x_1, y_1) \), we can use the point-slope form. The slope of the perpendicular line is \( -\displaystyle \frac{1}{m} \), so the equation of the perpendicular line will be:
\[ y - y_1 = -\frac{1}{m} (x - x_1). \]
In this equation, \( (x_1, y_1) \) is the point through which the perpendicular line passes, while \( m \) is the slope of the original line. The formula describes a line that has the opposite and reciprocal slope compared to the original line.
If the original line is represented by the equation \( y = mx + b \), the perpendicular line will have slope \( m_\perp = -\displaystyle \frac{1}{m} \) and be written in the form \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), where \( (x_1, y_1) \) is the point of intersection between the original line and the perpendicular line.
This property of perpendicular lines is fundamental in many areas of geometry, trigonometry, and physics, particularly when studying angles and perpendicular trajectories.
Worked Examples on Lines
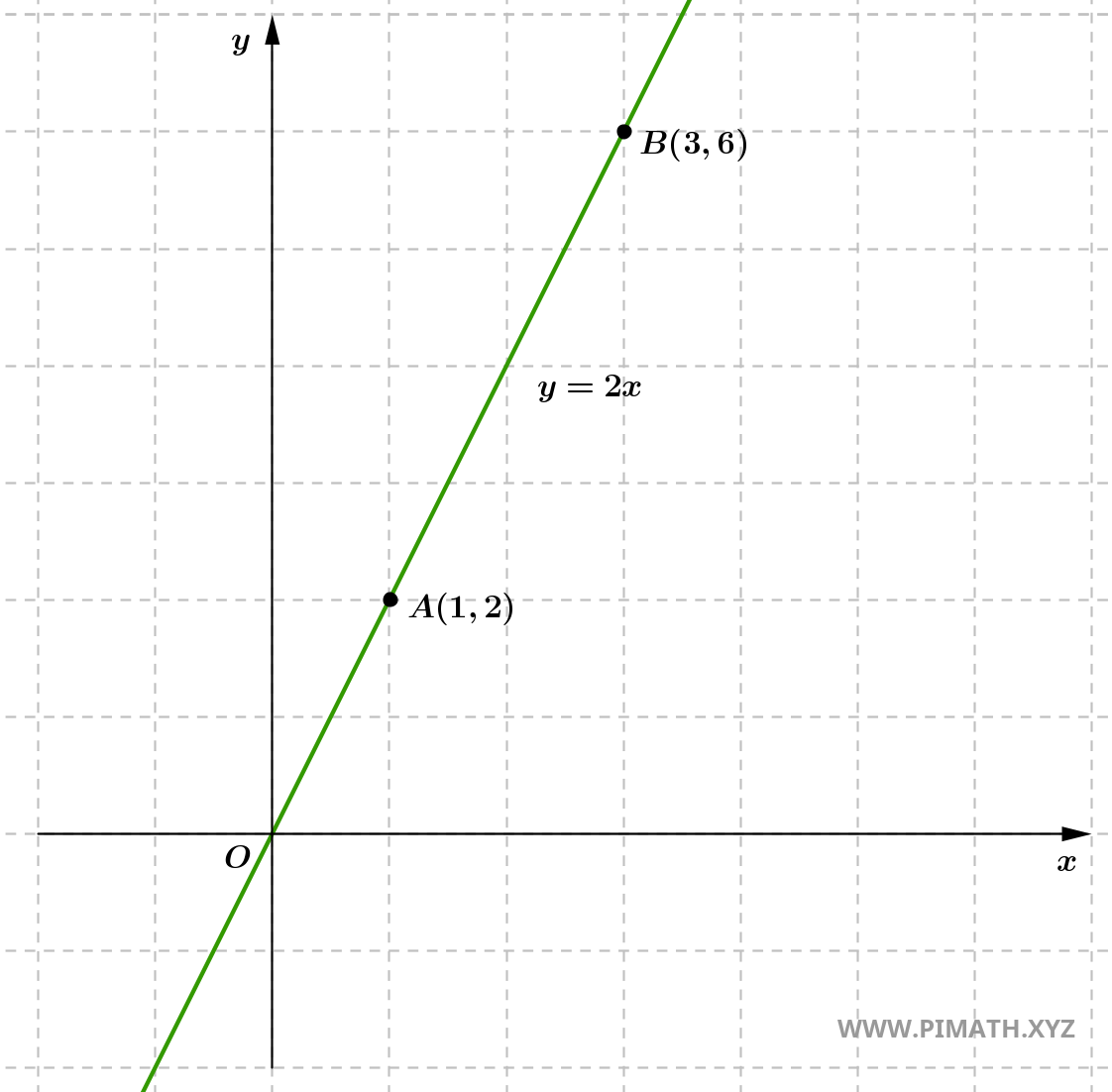
Example 1: Find the explicit equation of the line passing through \( A(1, 2) \) and \( B(3, 6) \).
Solution. We calculate the slope of the line:
\[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- We use the point-slope equation to determine the equation of the line passing through \( A(1, 2) \) with slope \( m = 2 \): \[ y - 2 = 2(x - 1). \]
- Expanding the equation: \[ y - 2 = 2x - 2. \]
- Simplifying: \[ y = 2x - 2 + 2 = 2x. \]
Therefore, the equation of the line passing through points \( A(1, 2) \) and \( B(3, 6) \) is \[ y = 2x. \]
Verification: We can verify that both points satisfy this equation:
- For \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
- For \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]
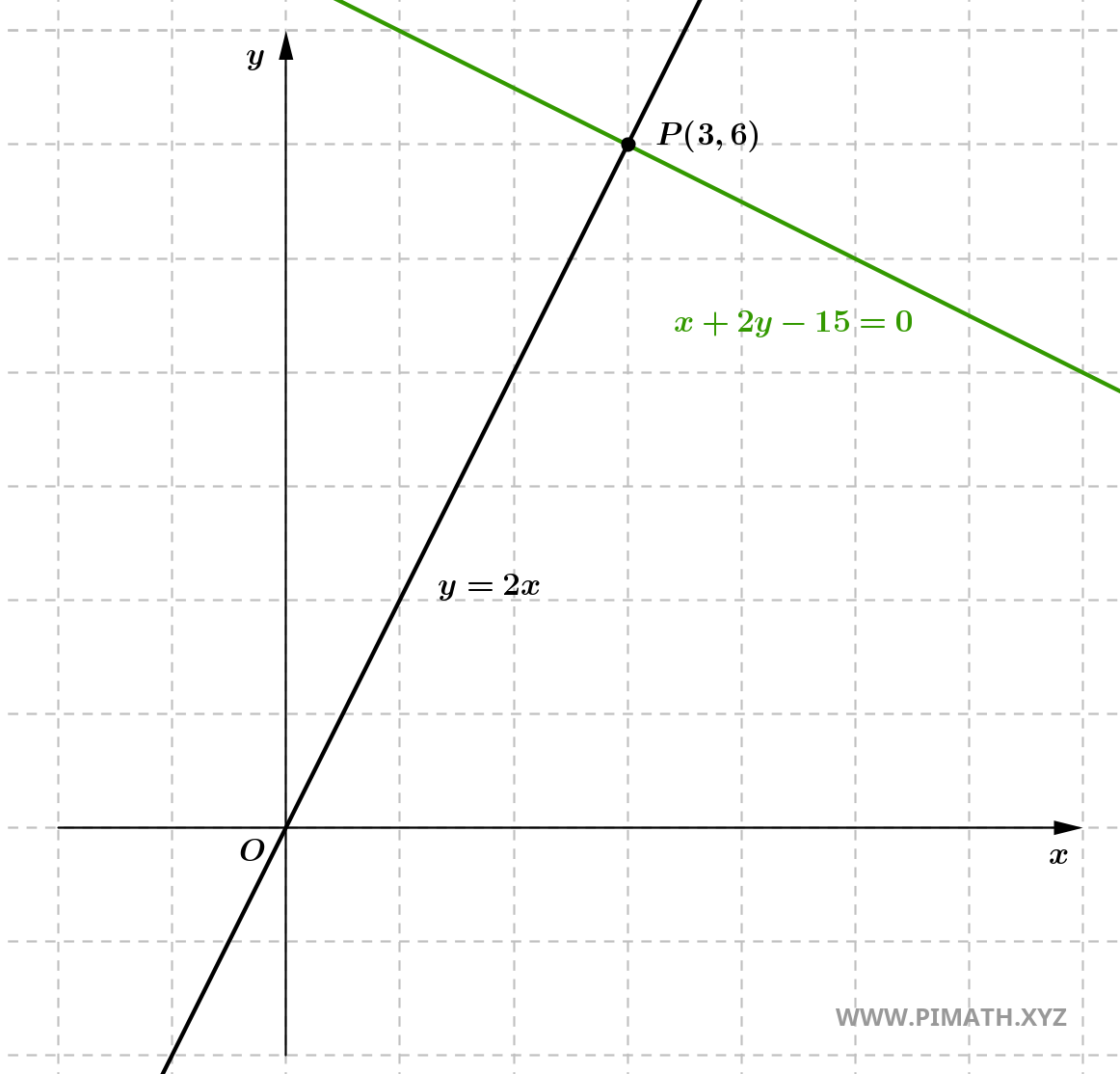
Example 2: Find the equation of the line perpendicular to the line \( y = 2x \) and passing through point \( P(3, 6) \).
Solution. The given line has slope \( m = 2 \). The slope of the perpendicular line will be:
\[ m_{\perp} = -\frac{1}{2}. \]
- We use the point-slope equation to determine the equation of the line passing through \( P(3, 6) \) with slope \( m_{\perp} = -\frac{1}{2} \): \[ y - 6 = -\frac{1}{2}(x - 3). \]
- We expand the equation: \[ y - 6 = -\frac{1}{2}x + \frac{3}{2}. \]
- We move the constant term to the right: \[ y = -\frac{1}{2}x + \frac{3}{2} + 6 = -\frac{1}{2}x + \frac{15}{2}. \]
Therefore, the equation of the desired line is: \[ y = -\frac{1}{2}x + \frac{15}{2}. \]
Implicit form: We multiply both sides by 2:
\[ 2y = -x + 15 \quad \Rightarrow \quad x + 2y - 15 = 0. \]
Verification: Substituting the coordinates of \( P(3, 6) \) into the explicit equation:
- \[ y = -\frac{1}{2}x + \frac{15}{2} \quad \Rightarrow \quad 6 = -\frac{1}{2} \cdot 3 + \frac{15}{2} = -\frac{3}{2} + \frac{15}{2} = \frac{12}{2} = 6. \]
The point lies on the line, so the solution is correct.
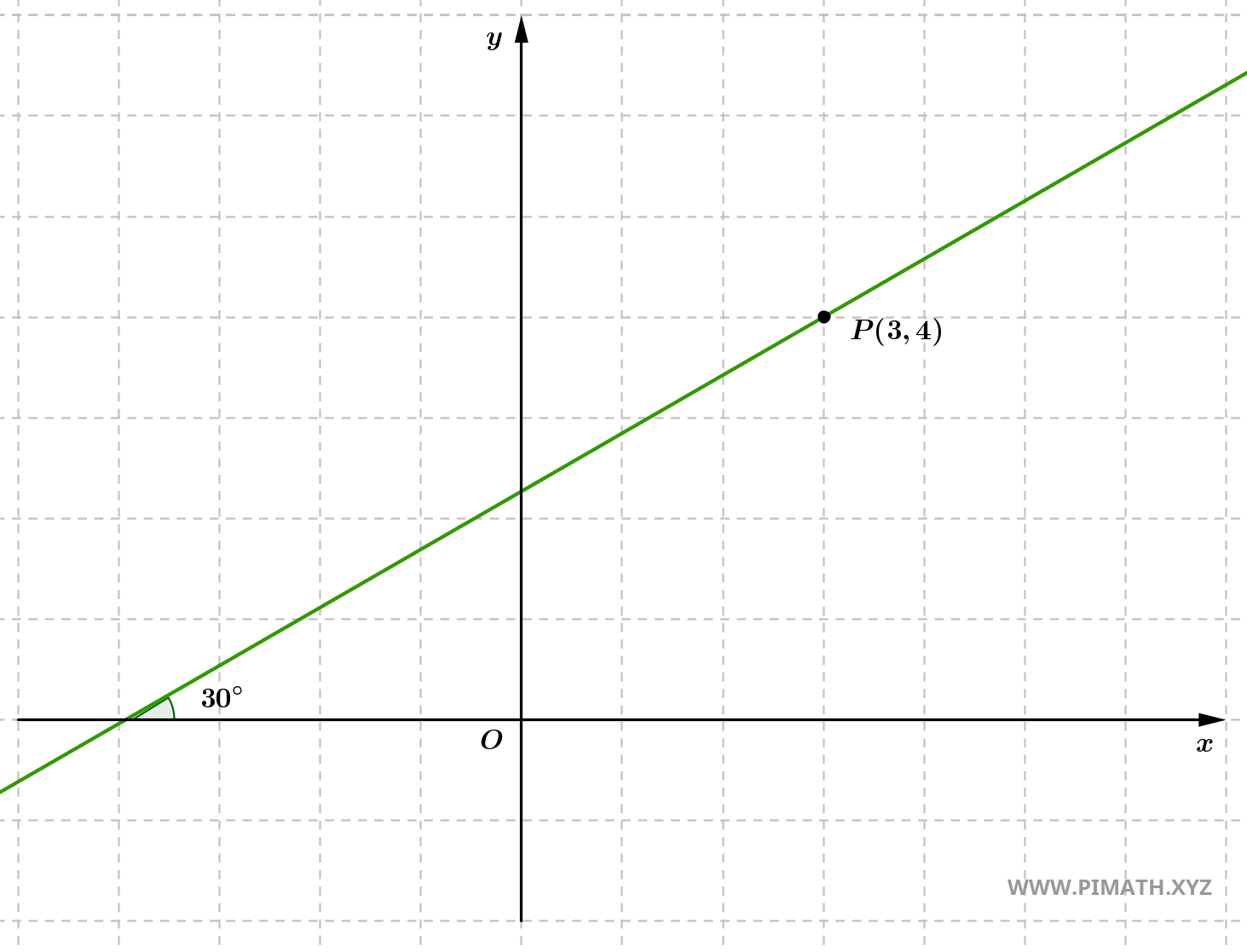
Example 3: Find the equation of the line passing through point \( P(3, 4) \) and forming a \( 30^\circ \) angle with the x-axis.
Solution. The angle that a line forms with the x-axis is related to the slope through the tangent:
\[ m = \tan(30^\circ) = \tan\left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}}. \]
- We use the point-slope equation with point \( P(3, 4) \) and slope \( m = \frac{1}{\sqrt{3}} \): \[ y - 4 = \frac{1}{\sqrt{3}}(x - 3). \]
- Expanding the equation: \[ y - 4 = \frac{1}{\sqrt{3}}x - \frac{3}{\sqrt{3}} = \frac{1}{\sqrt{3}}x - \sqrt{3}. \]
- Adding 4 to both sides: \[ y = \frac{1}{\sqrt{3}}x - \sqrt{3} + 4. \]
- Simplifying the constant term: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Therefore, the equation of the desired line is: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Verification: Substituting \( x = 3 \), we get: \[ y = \frac{1}{\sqrt{3}} \cdot 3 + (4 - \sqrt{3}) = \sqrt{3} + 4 - \sqrt{3} = 4. \]
- Point \( P(3, 4) \) lies on the line, so the solution is correct.
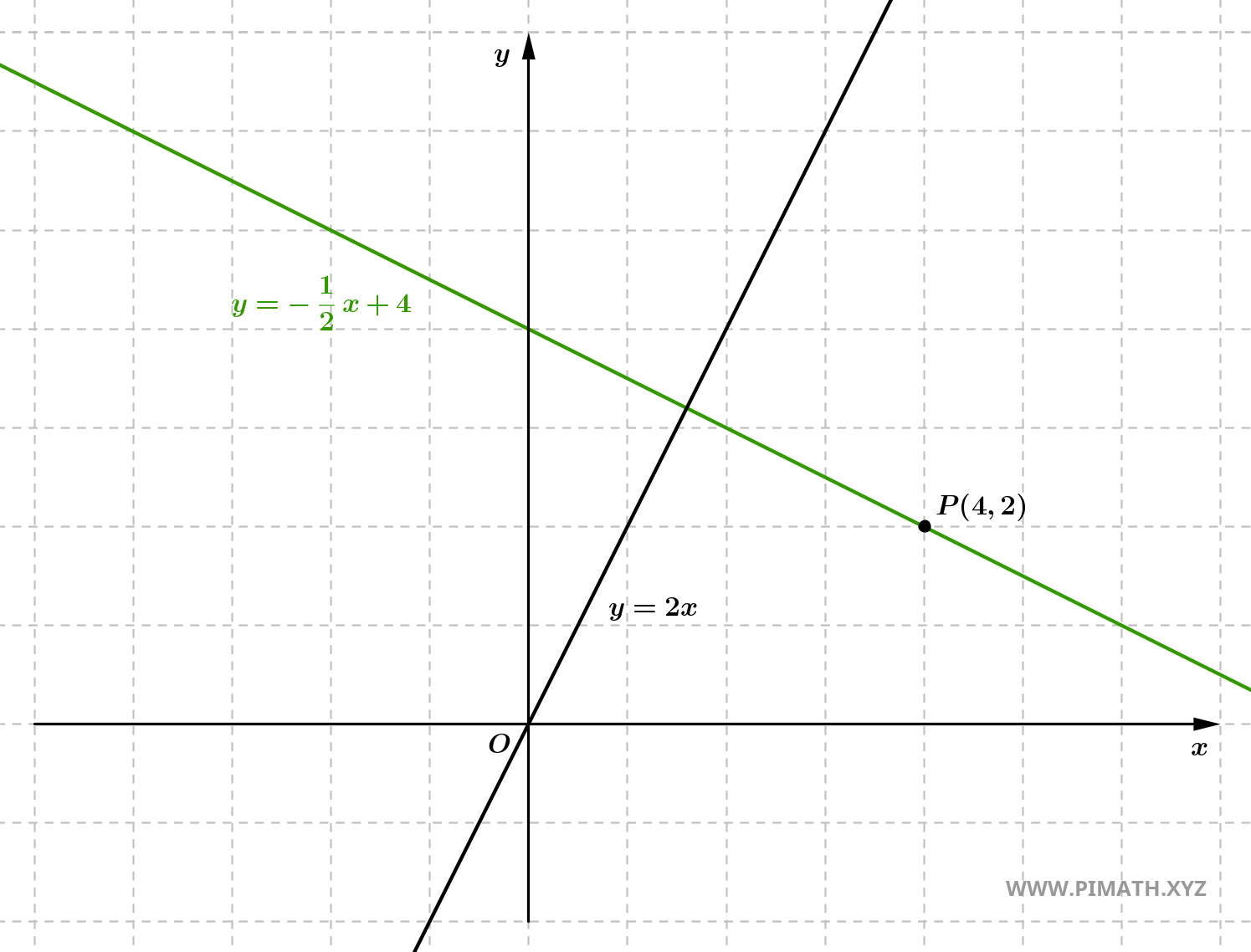
Example 4: Find the equation of the line perpendicular to the line \( y = 2x \) and passing through point \( P(4, 2) \).
Solution. The given line has slope \( m = 2 \). The slope of the perpendicular line will be:
\[ m_{\perp} = -\frac{1}{2}. \]
- We use the point-slope equation to determine the equation of the line passing through \( P(4, 2) \) with slope \( m_{\perp} = -\frac{1}{2} \): \[ y - 2 = -\frac{1}{2}(x - 4). \]
- We expand the equation: \[ y - 2 = -\frac{1}{2}x + 2. \]
- We move the constant term to the right: \[ y = -\frac{1}{2}x + 2 + 2 = -\frac{1}{2}x + 4. \]
Therefore, the equation of the desired line is: \[ y = -\frac{1}{2}x + 4. \]
Implicit form: We multiply both sides by 2:
\[ 2y = -x + 8 \quad \Rightarrow \quad x + 2y - 8 = 0. \]
Verification: Substituting the coordinates of \( P(4, 2) \) into the explicit equation:
- \[ y = -\frac{1}{2}x + 4 \quad \Rightarrow \quad 2 = -\frac{1}{2} \cdot 4 + 4 = -2 + 4 = 2. \]
The point lies on the line, so the solution is correct.
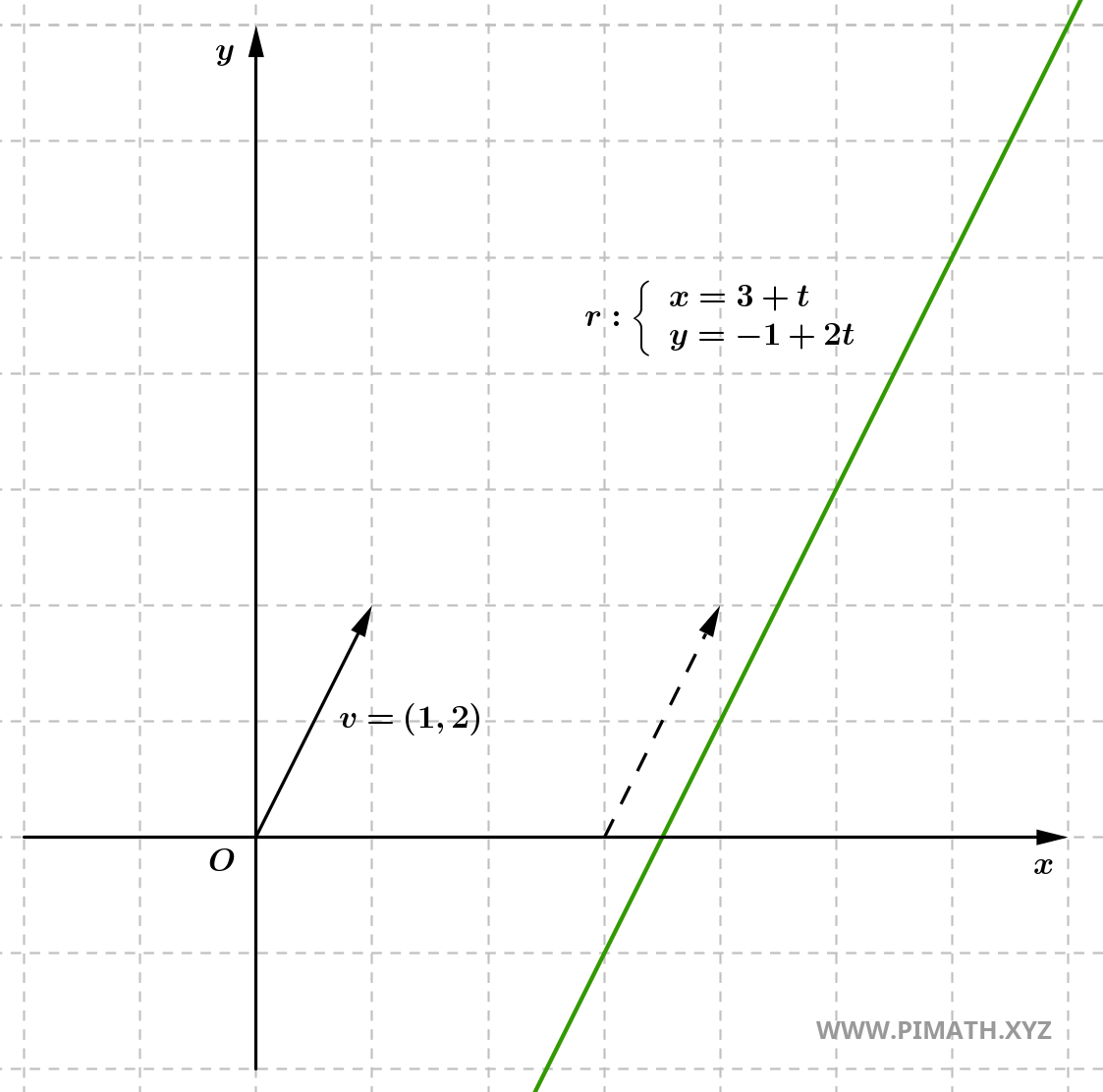
Example 5: Write the parametric equation of the line passing through \( A(3, -1) \) and \( B(4, 1) \). Then, write the parametric equation in Cartesian form.
Solution. We calculate the direction vector \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), which represents the direction of the line:
\[ \boldsymbol{v} = (4 - 3,\ 1 - (-1)) = (1,\ 2). \]
The parametric equations of the line are:
\[ \ell: \begin{cases} x = 3 + t \\ y = -1 + 2t \end{cases} \quad \text{where} \quad t \in \mathbb{R}. \]
Now let's convert to Cartesian form. We solve for \( t \) from the first equation:
\[ x = 3 + t \quad \Rightarrow \quad t = x - 3. \]
Substituting into the second equation:
\[ y = -1 + 2(x - 3) = -1 + 2x - 6 = 2x - 7. \]
Thus the explicit form is:
\[ y = 2x - 7. \]
Finally, moving everything to the left side gives us the implicit form:
\[ 2x - y - 7 = 0. \]