Rolle's Theorem is a fundamental result applicable to continuous and differentiable functions. This theorem states that, if a function \( f \) is continuous on a closed interval \([a,b]\), differentiable on the open interval \((a,b)\) and takes the same value at the endpoints \( f(a) = f(b) \), then there exists at least one interior point \( \xi \in (a,b) \) where the derivative of the function vanishes, that is \( f'(\xi) = 0 \). This result has numerous applications, including the proof of the Mean Value Theorem.
Table of Contents
Rolle's Theorem
Let \( f : [a,b] \to \mathbb{R} \) be a function continuous on the closed interval \([a,b]\), differentiable on the open interval \((a,b)\) and such that \( f(a) = f(b) \). Then there exists at least one point \( \xi \in (a,b) \) such that: \[ f'(\xi) = 0 \]
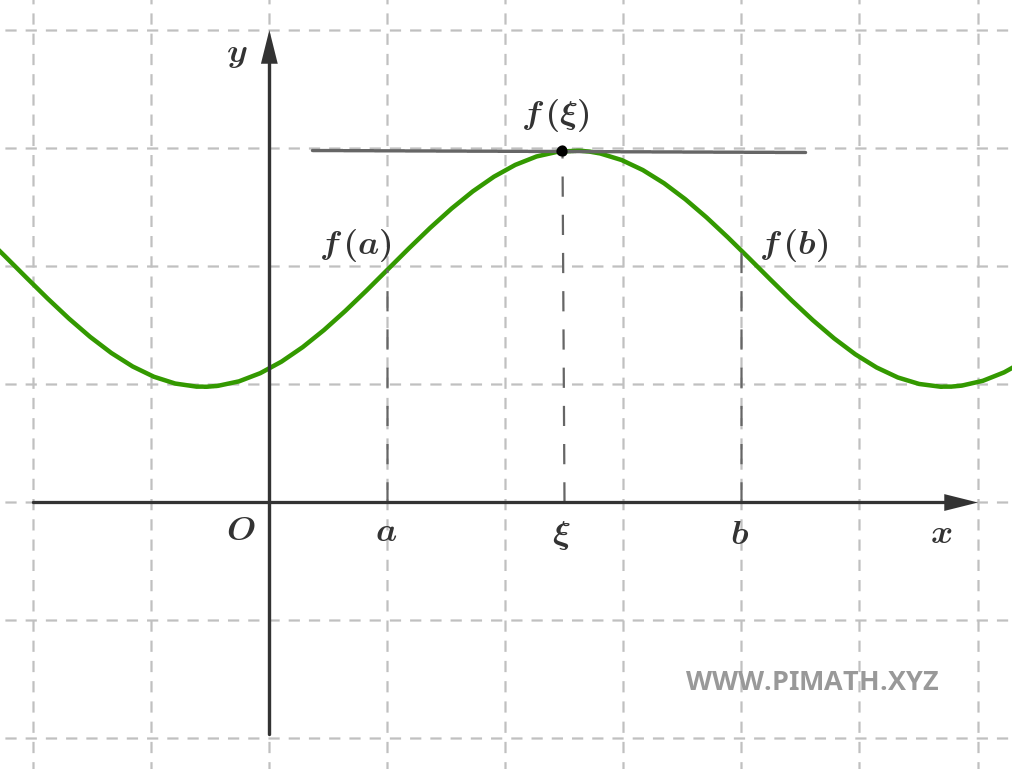
Proof. First, since \( f \) is continuous on \([a,b]\), by the Weierstrass Theorem it attains its absolute maximum and minimum on the interval. Therefore, there exist points \( c, d \in [a,b] \) such that: \[ f(c) = M \quad \text{and} \quad f(d) = m \] where \( M = \max_{x \in [a,b]} f(x) \) and \( m = \min_{x \in [a,b]} f(x) \).
Consider first the case where the function \( f \) is constant, namely \( f(x) = k \) for every \( x \in [a,b] \). In this case, by definition of derivative: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{k - k}{h} = 0 \] for every \( x \in (a,b) \). The thesis is thus immediately verified.
Let us now consider the case where \( f \) is not constant. Since \( f(a) = f(b) \), the absolute maximum and minimum cannot both be located at the endpoints \( a \) and \( b \). There must exist at least one point \( \xi \in (a,b) \) where \( f(\xi) = M \) or \( f(\xi) = m \). In both cases, \( \xi \) represents a point of local maximum or minimum.
Let \( \xi \) be a point of local maximum. For \( h \) sufficiently small:
\[ f(\xi + h) \leq f(\xi) \]
We can then consider the difference quotients:
\[ \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \quad \text{if} \ h > 0 \]
\[ \frac{f(\xi + h) - f(\xi)}{h} \geq 0 \quad \text{if} \ h < 0 \]
Since \( f \) is differentiable at \( \xi \), the limit of the difference quotient exists, namely: \[ f'(\xi) = \lim_{h \to 0} \frac{f(\xi + h) - f(\xi)}{h} \]
From what stated above, we have:
\[ \lim_{h \to 0^+} \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \leq \lim_{h \to 0^-} \frac{f(\xi + h) - f(\xi)}{h} \]
Therefore, necessarily: \[ f'(\xi) = 0 \]
An analogous reasoning applies in the case where \( \xi \) is a point of local minimum.
We have thus proved that there exists at least one point \( \xi \in (a,b) \) such that \( f'(\xi) = 0 \), completing the proof of Rolle's Theorem.

