Quadratic Equations: Formulas, Proofs and Solved Exercises

An equation is quadratic if and only if it can be written in the following form:

\[ a x ^ 2 + b x + c = 0 \quad , \quad a \neq 0 \]

called the standard form. The real numbers \( a , b \) and \( c \) are called the quadratic coefficient, linear coefficient and constant term.

We can always assume that the quadratic coefficient is positive. Indeed, in the case where \( a < 0 \), we simply multiply both sides by \( -1 \) to reduce to the case \( a > 0 \).

Contents

• Completing the Square
• Reduced Formula
• Monomial Quadratic Equations
• Pure Quadratic Equations
• Incomplete Quadratic Equations
• Relationship between Sum and Product of Roots
• Solved Exercises
• Geometric Meaning

In this section we will derive the general formula for solving any quadratic equation. We start from the standard form:

\[ ax^2 + bx + c = 0, \quad a \neq 0 \]

To simplify the calculations, we divide everything by \( a \), so as to make the coefficient of the quadratic term equal to 1:

\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]

Now, we isolate the constant term by moving it to the right-hand side:

\[ x^2 + \frac{b}{a}x = -\frac{c}{a} \]

At this point, we apply the completing the square method. The trick consists of adding and subtracting a quantity to transform the left-hand side into a perfect square. In this case, the missing term is

\[ \left(\frac{b}{2a}\right)^2 \]

Let's add it to both sides:

\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 \]

The left-hand side is now the square of a binomial, so we can write it as

\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2} \]

We rewrite the right-hand side with a common denominator:

\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} \]

Now we can extract the square root from both sides, remembering that \( \sqrt{x^2} = |x| \):

\[ \left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a} \]

From here we obtain \( x \) directly:

\[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]

Finally, we isolate \( x \) and obtain the famous quadratic formula:

\[ x_{1,2} = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]

The term under the square root, known as the discriminant and denoted by \( \Delta \), is defined as:

\[ \Delta = b^2 - 4ac \]

But what does the discriminant represent? It allows us to determine at a glance the type of solutions the equation will have. Let's analyze it in the three possible cases:

• \( \Delta > 0 \): the discriminant is positive, so the square root is a real number. This means that the equation has two distinct real solutions.
• \( \Delta = 0 \): the square root of zero is zero, so the formula gives us a single repeated solution. In other words, the equation has two coincident solutions (or a double root).
• \( \Delta < 0 \): the square root of a negative number is not a real number, so the equation has no real solutions, but two complex solutions with imaginary parts.

This means that by looking only at the value of \( \Delta \), we can predict the nature of the solutions without having to solve the equation directly.

The reduced formula is a simplified version of the quadratic formula, useful when the coefficient \( b \) is even.

Consider a quadratic equation in standard form:

\[ ax^2 + bx + c = 0 \]

If the coefficient \( b \) is even, we can write it as:

\[ b = 2k \]

Substituting into the equation we get:

\[ ax^2 + 2kx + c = 0 \]

The classic quadratic formula is:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Substituting \( b = 2k \):

\[ x = \frac{-2k \pm \sqrt{(2k)^2 - 4ac}}{2a} \]

\[ x = \frac{-2k \pm \sqrt{4k^2 - 4ac}}{2a} \]

\[ x = \frac{-2k \pm 2\sqrt{k^2 - ac}}{2a} \]

Dividing numerator and denominator by 2:

\[ x = \frac{-k \pm \sqrt{k^2 - ac}}{a} \]

Finally, we can express the reduced formula as:

\[ x = \frac{-\frac{b}{2} \pm \sqrt{\left(\frac{b}{2}\right)^2 - ac}}{a} \]

The reduced discriminant is given by:

\[ \Delta' = \left(\frac{b}{2}\right)^2 - ac \]

Now let's compare it with the discriminant of the complete formula:

\[ \Delta = b^2 - 4ac \]

Substituting \( b = 2k \), we get:

\[ \Delta = (2k)^2 - 4ac \]

\[ \Delta = 4k^2 - 4ac \]

Dividing everything by 4:

\[ \frac{\Delta}{4} = k^2 - ac \]

Since \( k = \displaystyle \frac{b}{2} \), we can rewrite:

\[ \frac{\Delta}{4} = \left(\frac{b}{2}\right)^2 - ac \]

which is exactly the definition of \( \Delta' \).

Therefore, we can conclude that:

\[ \Delta' = \frac{\Delta}{4} \]

An equation is called monomial if it reduces to a single quadratic term, that is, of the form:

\[ ax^2 = 0 \]

To solve this equation, we divide both sides by \( a \) (assuming \( a \neq 0 \)):

\[ x^2 = 0 \]

Taking the square root, we get the solution:

\[ x = 0 \]

Although the value is unique, mathematically we consider two coincident solutions: \( x_1 = x_2 = 0 \).

An equation is called pure if, in the general form \( ax^2 + bx + c = 0 \), the coefficient \( b \) is zero, reducing to:

\[ ax^2 + c = 0 \]

To solve this equation, we move the constant term \( c \) to the right-hand side:

\[ ax^2 = -c \]

We divide both sides by \( a \neq 0 \):

\[ x^2 = -\frac{c}{a} \]

Solutions exist only if \( \displaystyle -\frac{c}{a} \geq 0 \), otherwise the equation has no real solutions. If the value under the square root is positive, we get:

\[ x_{1,2} = \pm \sqrt{-\frac{c}{a}} \]

An equation is called incomplete if the constant term is zero, that is:

\[ ax^2 + bx = 0 \]

In this case, we can solve it by factoring out \( x \) as a common factor:

\[ x (ax + b) = 0 \]

Applying the zero product property, we get the two solutions:

\[ x = 0 \quad \text{or} \quad x = -\frac{b}{a} \]

Consider the quadratic equation of the form \( ax^2 + bx + c = 0 \), where \( a \), \( b \) and \( c \) are the coefficients. Let \( x_1 \) and \( x_2 \) be the roots of this equation. Now, we want to write the equation in terms of the roots. A quadratic equation can be written as the product of the factors \( (x - x_1) \) and \( (x - x_2) \), so we can write:

\[ a(x - x_1)(x - x_2) = 0 \]

Expanding the product on the left, we get:

\[ a(x^2 - (x_1 + x_2)x + x_1x_2) = 0 \]

Now, by the distributive property, we get:

\[ ax^2 - a(x_1 + x_2)x + ax_1x_2 = 0 \]

At this point, we can compare this expression with the standard equation \( ax^2 + bx + c = 0 \). In particular, we see that the coefficients must be equal. Comparing the linear term, we get:

\[ -a(x_1 + x_2) = b \]

Solving for \( x_1 + x_2 \), we get:

\[ x_1 + x_2 = -\frac{b}{a} \]

Similarly, comparing the constant term, we get:

\[ ax_1x_2 = c \]

Solving for the product of the roots, we get:

\[ x_1 \cdot x_2 = \frac{c}{a} \]

In summary, the roots \( x_1 \) and \( x_2 \) are related to the coefficients \( a \), \( b \) and \( c \) through these two simple relationships: the sum of the roots is \( \displaystyle -\frac{b}{a} \) and the product of the roots is \( \displaystyle \frac{c}{a} \). These properties are fundamental and allow us to deduce important information about the roots without calculating them directly.

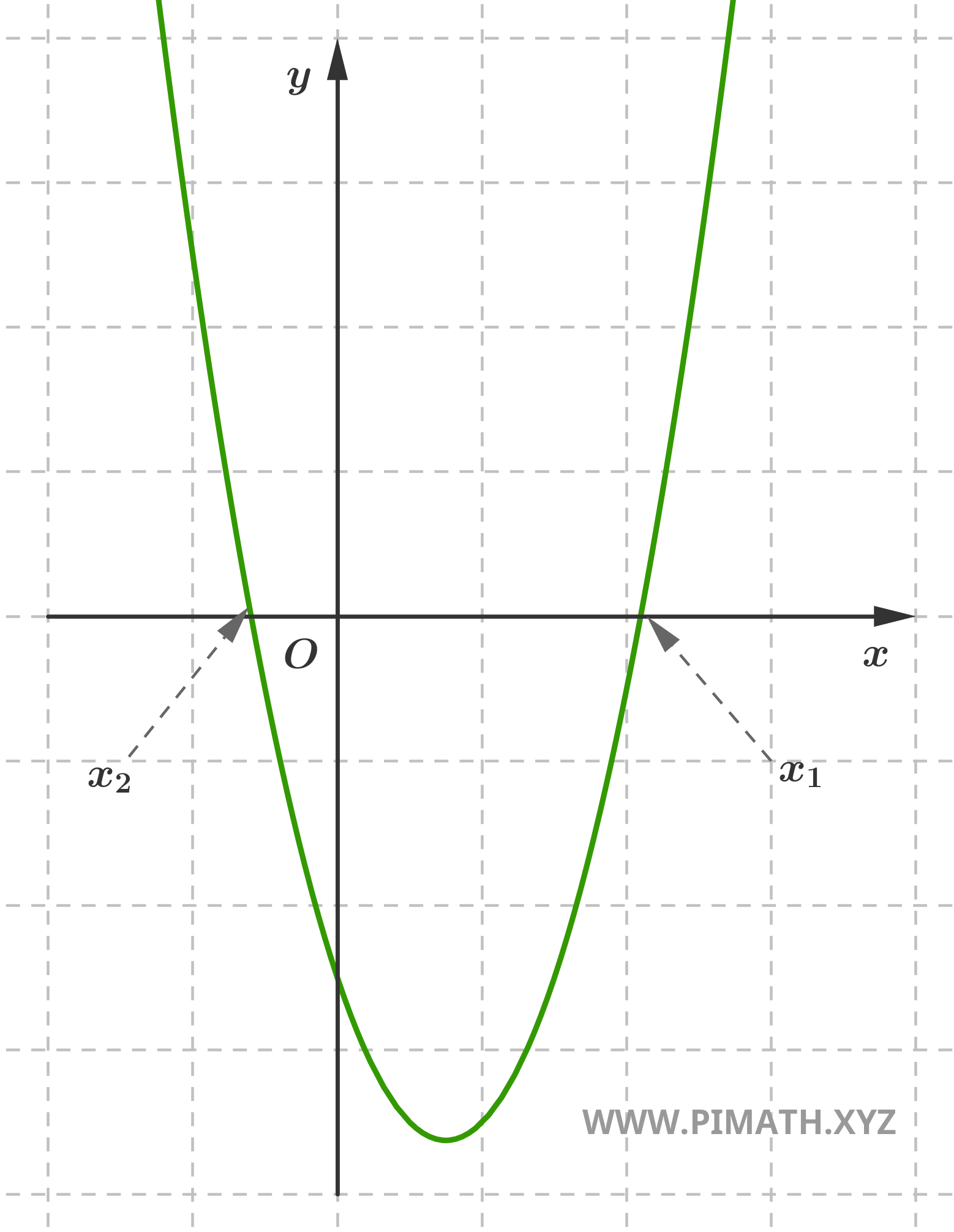
Example 1. Solve the quadratic equation \( x^2 - 3x - 5 = 0 \).

Solution. To solve it, we use the following formula:

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

In this case, the coefficients are \( a = 1 \), \( b = -3 \) and \( c = -5 \). Applying the formula:

\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-5)}}{2(1)} = \frac{3 \pm \sqrt{9 + 20}}{2} = \frac{3 \pm \sqrt{29}}{2} \]

The solutions are therefore:

\[ x_1 = \frac{3 + \sqrt{29}}{2} \quad , \quad  x_2 = \frac{3 - \sqrt{29}}{2} \]

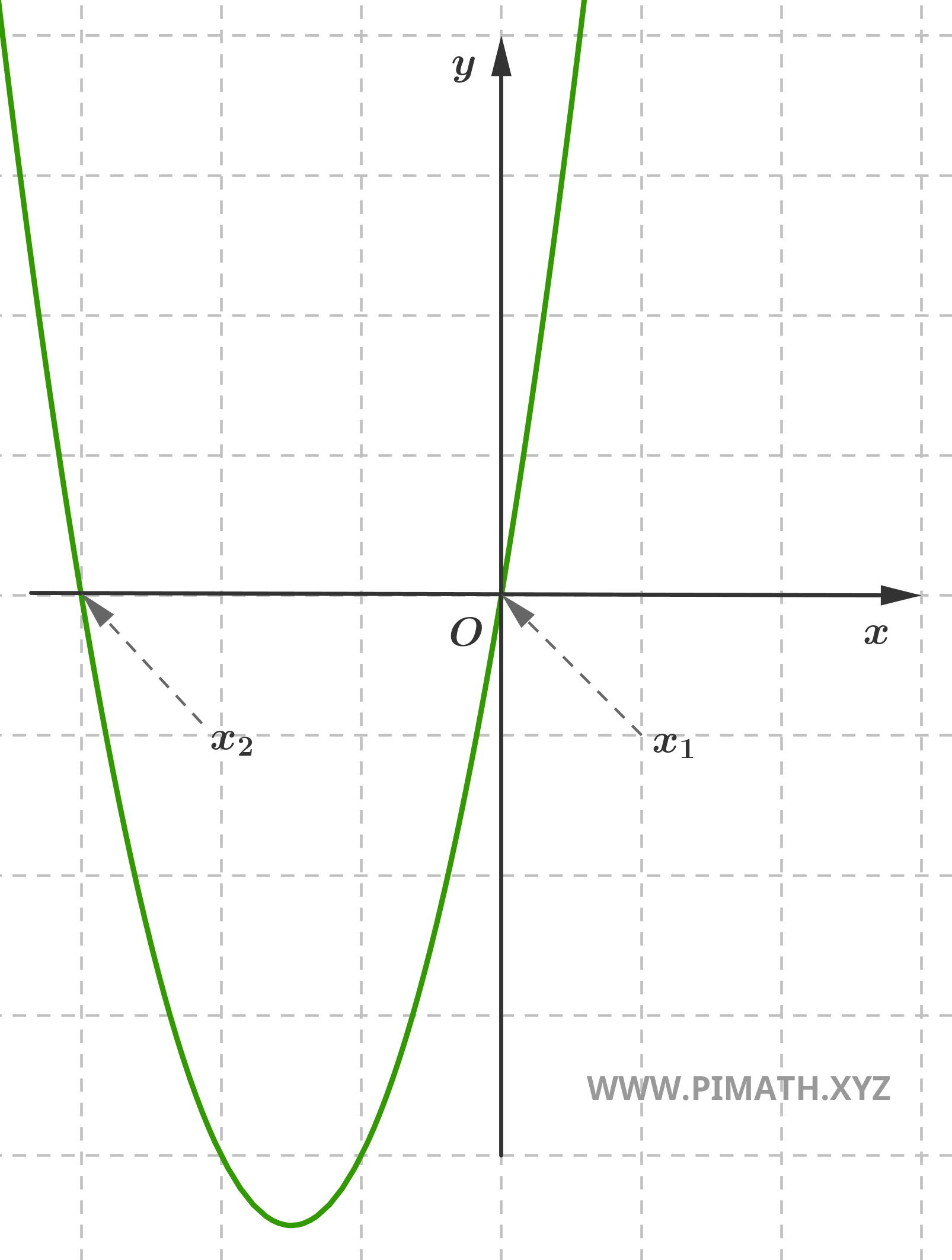
Example 2 (reduced form). Find the solutions of the following equation \( x^2 + 6x = 0 \).

Solution. To solve it, we can factor out the common factor:

\[ x(x + 6) = 0 \]

The solutions are therefore: \( x_1 = 0 \) and \( x_2 = -6 \).

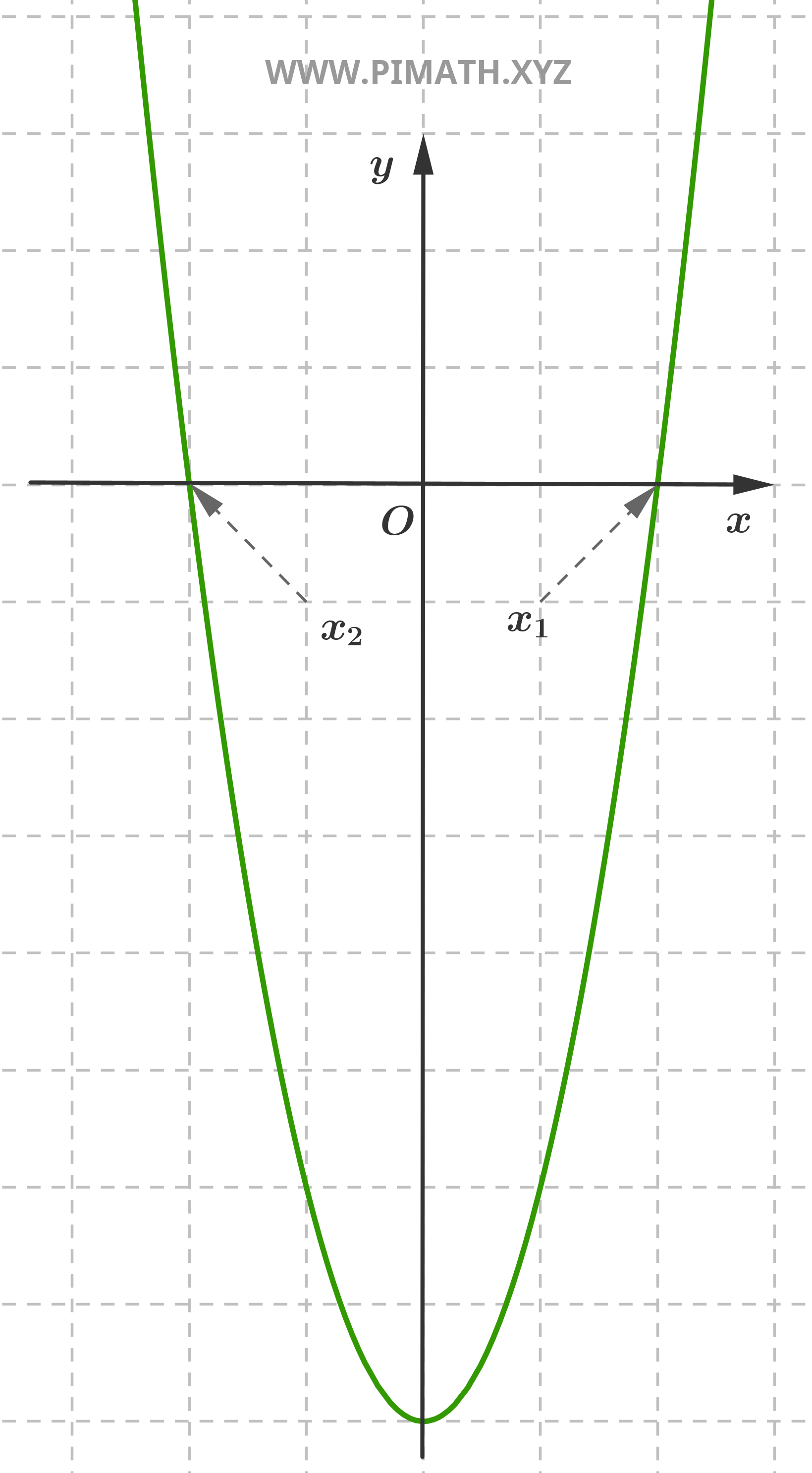
Example 3 (pure equation). Find the solutions of the equation \( x^2 = 16 \).

Solution. To solve it, we can take the square root of both sides:

\[ x = \pm \sqrt{16} = \pm 4 \]

The solutions are therefore: \( x_1 = 4 \) and \( x_2 = -4 \).

Example 4 (pure equation). Find the solutions of the equation \( x^2 + 9 = 0 \).

Solution. We isolate \( x^2 \):

\[ x^2 = -9 \]

Since there are no real numbers that satisfy this equation, the equation has no real solutions.

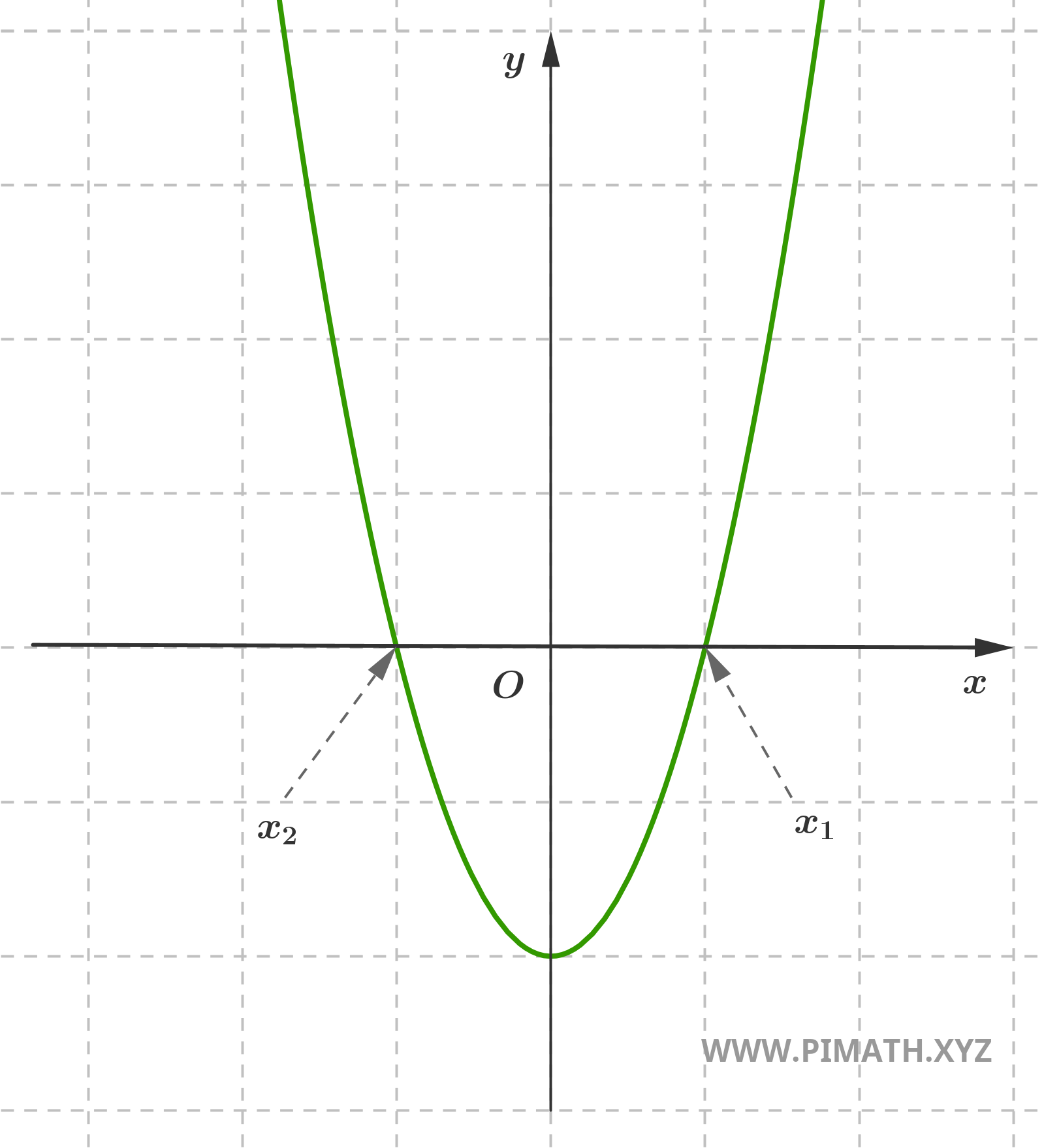
Example 5. Find the solutions of the following equation \( x^2 - 4 = 0 \).

Solution. We isolate \( x^2 \):

\[ x^2 = 4 \]

Now we take the square root of both sides:

\[ x = \pm \sqrt{4} = \pm 2 \]

The solutions are therefore:

\[ x_1 = 2 \quad , \quad x_2 = -2 \]

From a geometric point of view, solving a quadratic equation means finding the real values (if they exist) for which the parabola with equation \( y = ax^2 + bx + c \) intersects the x-axis or, if you prefer, the line \( y = 0 \).