The notable limits are fundamental expressions in mathematical analysis that describe the local behavior of functions at critical points.
These limits are essential tools for establishing continuity, differentiability, and for simplifying the analysis of the asymptotic behavior of more complex functions.
- Proof using the Comparison Criterion
- Proof using De L'Hôpital's Rule
- Proof using the Taylor Series Expansion
Proof using the Comparison Criterion
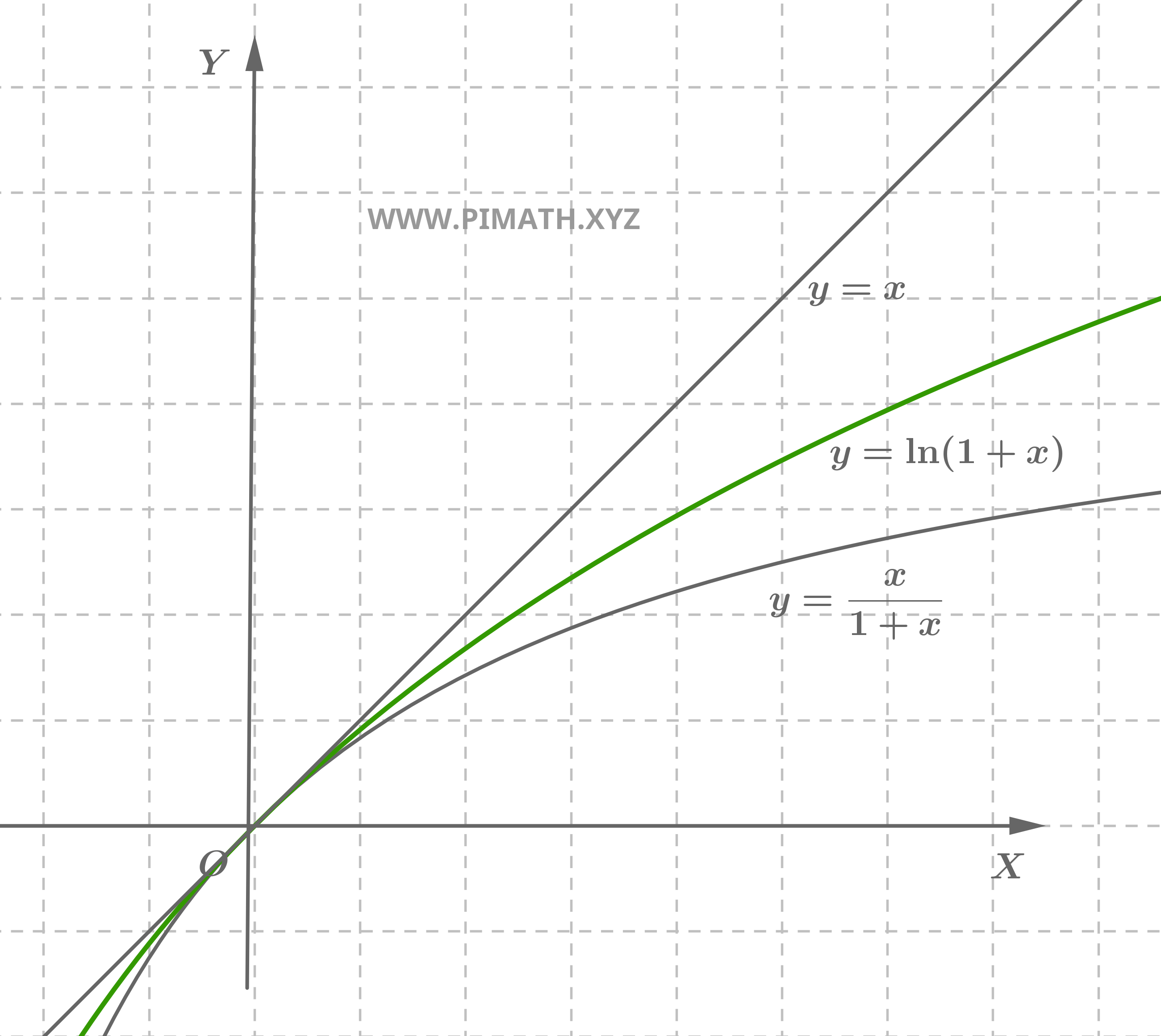
Consider the limit \[ \lim_{x \to 0} \frac{\ln(1+x)}{x}. \] For \( x > 0 \) we can use the concavity properties of the function \(\ln(1+x)\). In particular, knowing that the function is concave, it follows that the graph of \(\ln(1+x)\) lies below the tangent at \( x=0 \), that is: \[ \ln(1+x) \leq x. \]
Furthermore, it can be shown that for \( x > 0 \) the following inequality also holds: \[ \ln(1+x) \geq \frac{x}{1+x}. \] These inequalities can be summarized as: \[ \frac{x}{1+x} \leq \ln(1+x) \leq x. \]
Dividing by \( x \) (for \( x > 0 \)), we obtain: \[ \frac{1}{1+x} \leq \frac{\ln(1+x)}{x} \leq 1. \]
Now, we calculate the limits of the bounds as \( x \to 0 \): \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1 \quad \text{and} \quad \lim_{x \to 0} 1 = 1. \] By the Squeeze Theorem, it follows that: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Therefore, we have proven by comparison that: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
In this document we demonstrate the following notable limit:
Proof using De L'Hôpital's Rule
We observe that, by setting \( f(x) = \ln(1+x) \) and \( g(x) = x \), as \( x \) tends to zero we have \[ f(0) = \ln(1+0) = 0 \quad \text{and} \quad g(0) = 0, \] so the limit takes the indeterminate form \(\frac{0}{0}\). This condition allows us to apply De L'Hôpital's Rule.
Thus, we differentiate the numerator and the denominator:
\[ f'(x) = \frac{d}{dx}\ln(1+x) = \frac{1}{1+x}, \quad g'(x) = \frac{d}{dx}x = 1. \]
Applying De L'Hôpital's Rule, we obtain: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} = \lim_{x \to 0} \frac{1}{1+x}. \]
Since the limit \(\lim_{x \to 0} \frac{1}{1+x}\) is immediately calculable, we have: \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1. \]
Consequently, it follows that: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Proof using the Taylor Series Expansion
Alternatively, we can demonstrate the result by resorting to the Taylor series expansion of the function \(\ln(1+x)\) around \( x=0 \):
The Taylor series of \(\ln(1+x)\) is given by: \[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots, \quad \text{for } |x| < 1. \]
Dividing by \( x \), we obtain: \[ \frac{\ln(1+x)}{x} = 1 - \frac{x}{2} + \frac{x^2}{3} - \cdots. \]
Taking the limit as \( x \) tends to zero, all terms containing positive powers of \( x \) vanish, leaving: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
We have thus demonstrated that, by three methods, we obtain:
$$\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1.$$
The first proof used the comparison criterion, the second used De L'Hôpital's Rule, while the third was based on the Taylor series expansion.

