Even functions and odd functions are distinguished by their symmetries: even functions are symmetric with respect to the y-axis, while odd functions are symmetric with respect to the origin. We will also explore the behavior of the sum of functions: the sum of two even functions is still an even function, just as the sum of two odd functions is still odd. Finally, we will see how to decompose a function into its even part and its odd part.
- Even Functions
- Sum of two even functions
- Odd Functions
- Sum of two odd functions
- Functions neither even nor odd
- Integration over symmetric intervals
- Decomposition of a function into even and odd parts
- Proof of uniqueness of decomposition
Even Functions
Definition. A function \( f : X \to Y \) is called even if:
\[ \forall x \in X, \quad -x \in X \quad \text{and} \quad f(-x) = f(x) \]
In other words, the function is even if the domain is symmetric with respect to the origin and the function takes the same value at \( x \) and \( -x \).
Example. The function \( f(x) = x^2 \) is even, indeed for every \( x \in \mathbb{R} \), we have \( (-x)^2 = x^2 \).
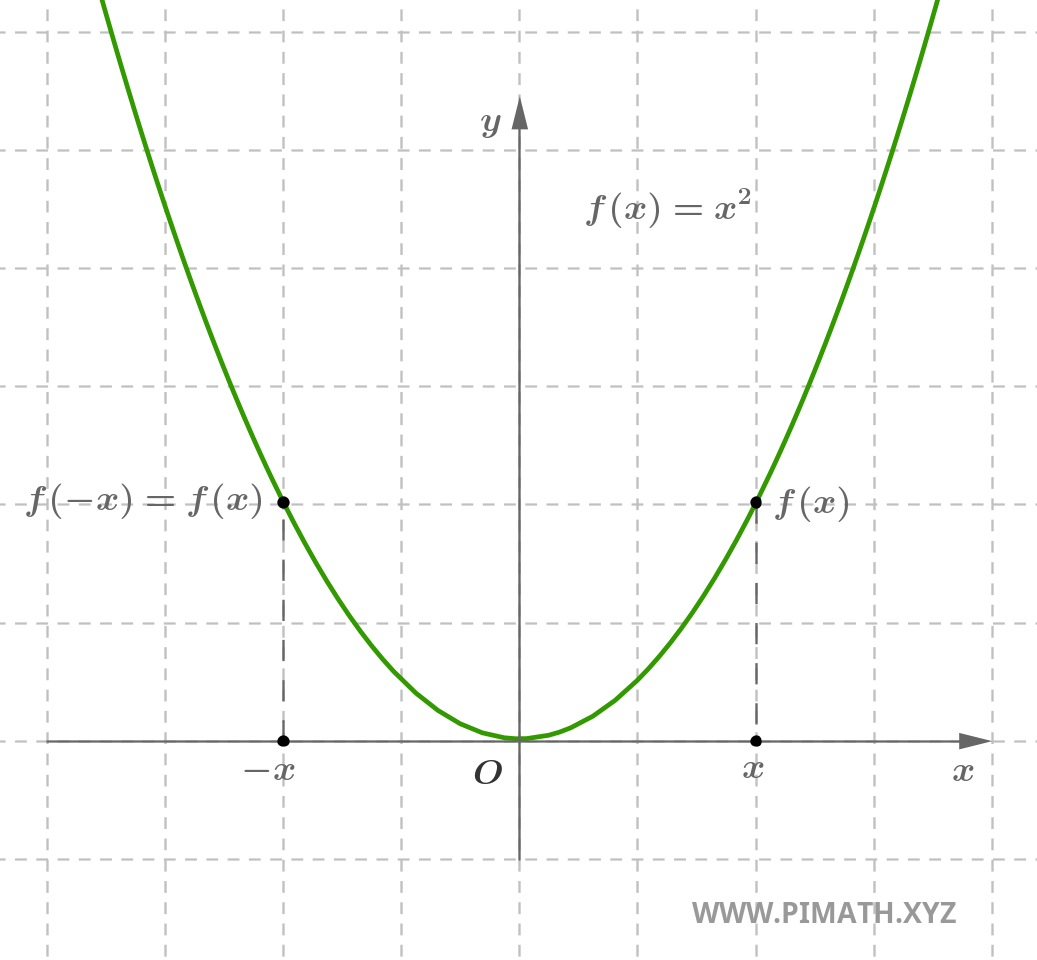
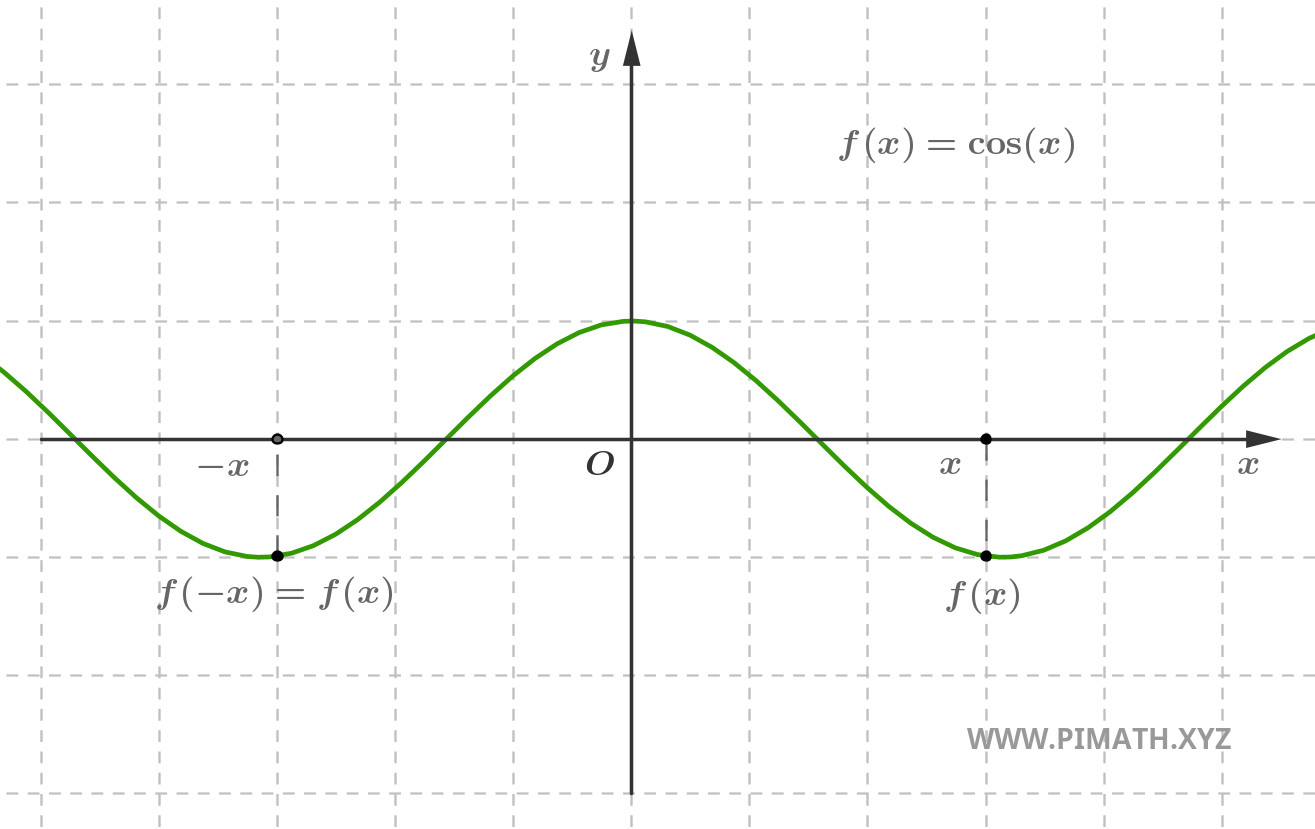
Example. The function \( f(x) = \cos(x) \) is even, indeed for every \( x \in \mathbb{R} \), we have \( \cos(-x) = \cos(x) \).
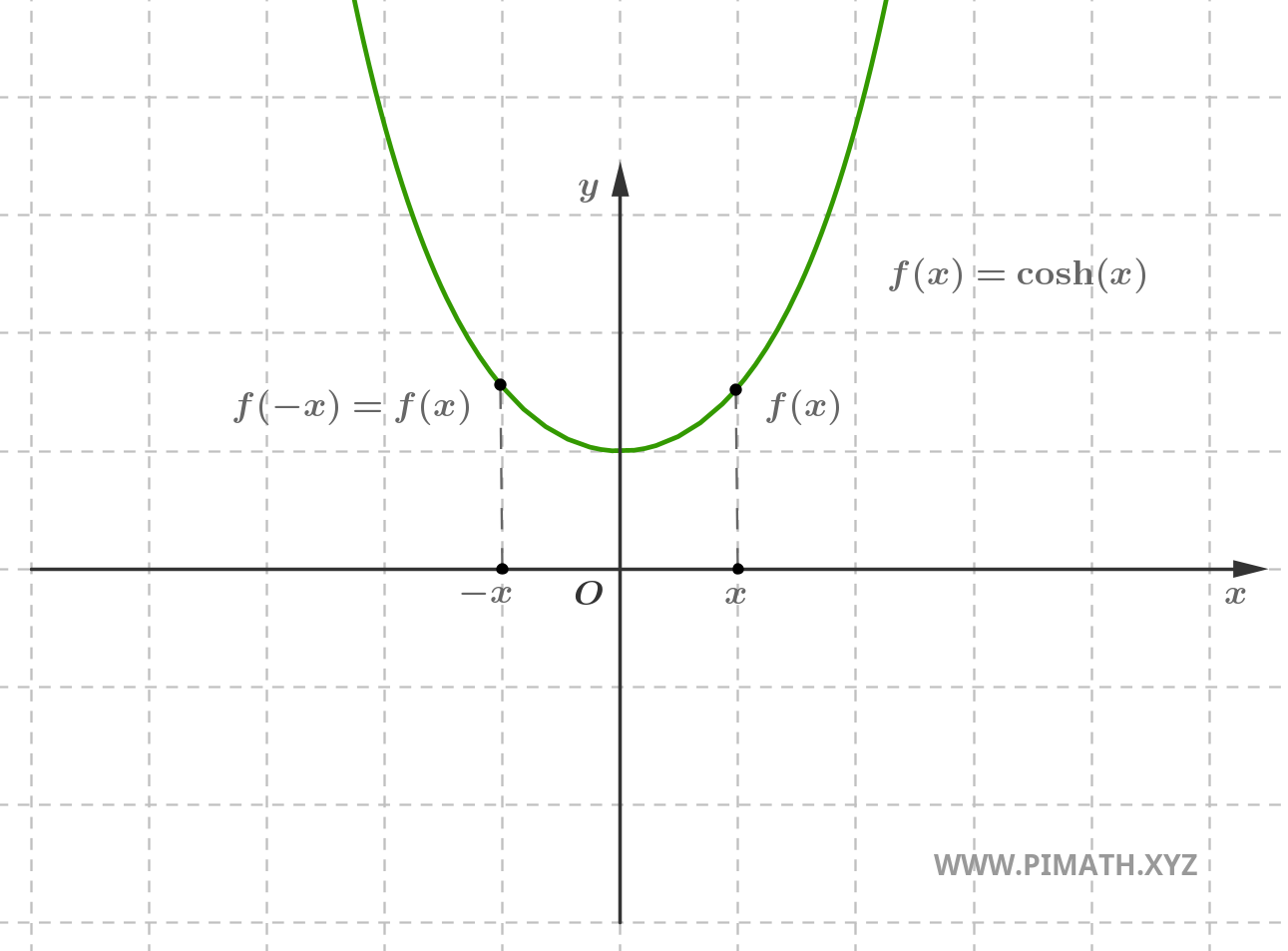
Example. The function \( f(x) = \cosh(x) \) is even, indeed for every \( x \in \mathbb{R} \), we have \( \cosh(-x) = \cosh(x) \).
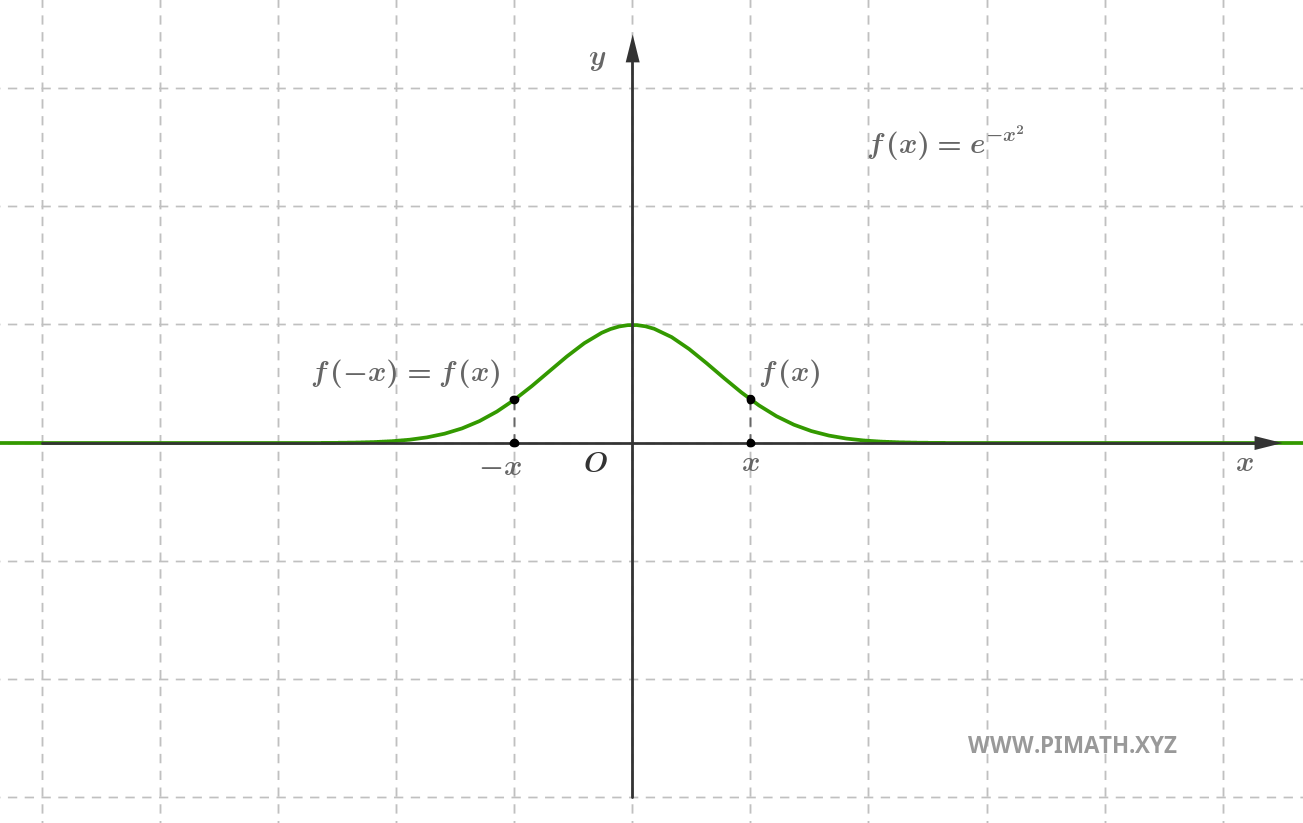
Example. The function \( f(x) = e^{-x^2} \) is even, indeed for every \( x \in \mathbb{R} \), we have \( e^{-(-x)^2} = e^{-x^2} \).
Sum of two even functions
Let \( f \) and \( g \) be two even functions, defined respectively on \( D_f \) and \( D_g \). Consider the sum function \( f + g \), defined on the domain \( D = D_f \cap D_g \). Since \( D_f \) and \( D_g \) are symmetric, the intersection \( D \) is also symmetric. For every \( x \in D \), we have:
\[ (f + g)(-x) = f(-x) + g(-x) = f(x) + g(x) = (f + g)(x) \]
therefore \( f + g \) is an even function.
An even function exhibits symmetry with respect to the y-axis. Therefore, to analyze its graph, it is sufficient to study it for \( x \geq 0 \); the part for \( x < 0 \) is obtained by symmetry.
Odd Functions
Definition. A function \( f : X \to Y \) is called odd if:
\[ \forall x \in X, \quad -x \in X \quad \text{and} \quad f(-x) = -f(x) \]
In other words, the function is odd if the domain is symmetric with respect to the origin and the function takes opposite values at \( x \) and \( -x \).
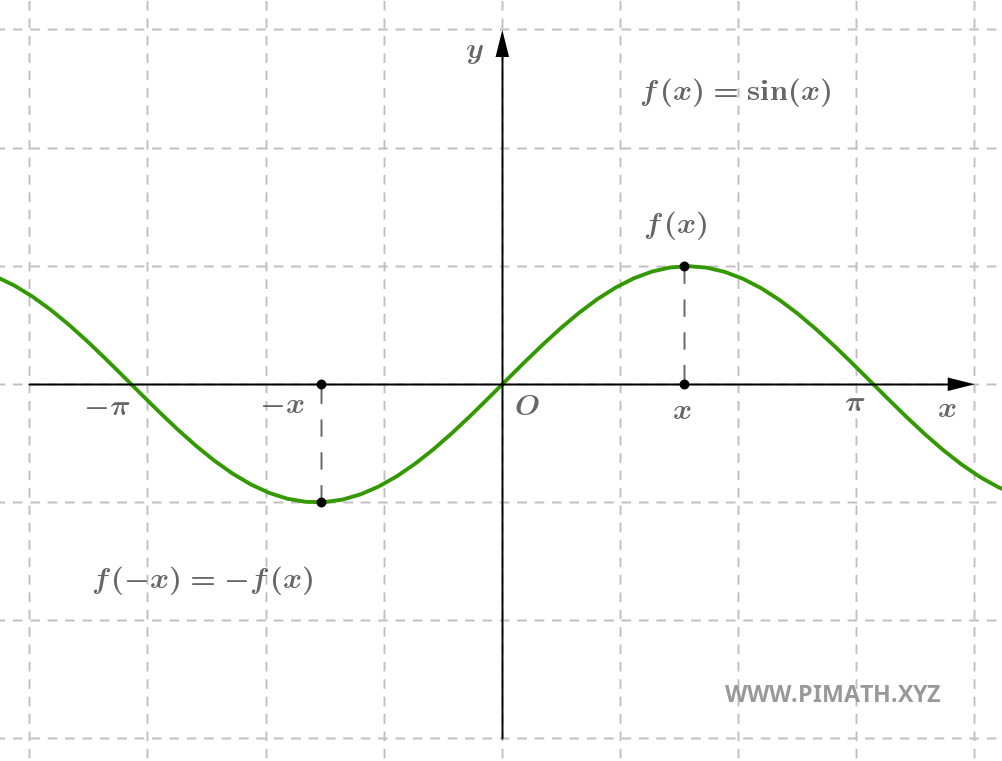
Example. The function \( f(x) = \sin(x) \) is odd, indeed for every \( x \in \mathbb{R} \), we have \( \sin(-x) = -\sin(x) \).
Example. The function \( f(x) = x^3 \) is odd, indeed for every \( x \in \mathbb{R} \), we have \( (-x)^3 = -x^3 \).
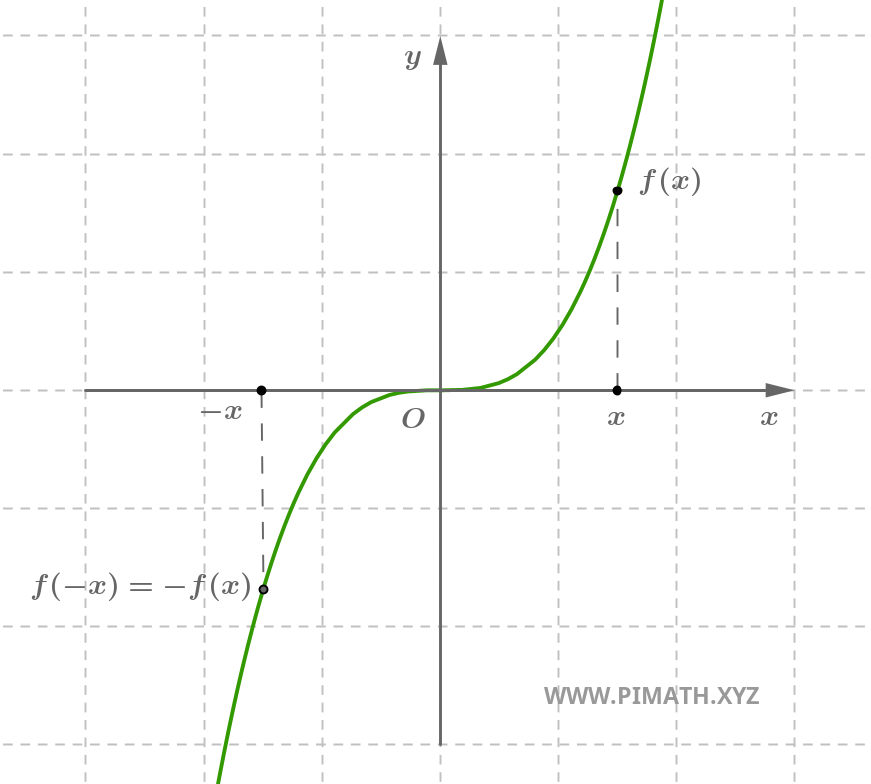
An odd function is symmetric with respect to the origin: rotating its graph 180° around the origin yields the same graph.
Sum of two odd functions
Let \( f \) and \( g \) be two odd functions, defined on domains \( D_f \) and \( D_g \). Then the sum \( f + g \), defined on the common domain \( D = D_f \cap D_g \), is also odd.
Indeed, for every \( x \in D \), we have:
\[ (f + g)(-x) = f(-x) + g(-x) = -f(x) - g(x) = -(f(x) + g(x)) = -(f + g)(x) \]
Therefore \( f + g \) is an odd function.
Functions neither even nor odd
If a function satisfies neither the relation \( f(-x) = f(x) \), nor \( f(-x) = -f(x) \), then it is neither even nor odd.
Example. The functions \( f(x) = e^x \) and \( f(x) = x + 1 \) are neither even nor odd.
Integration over symmetric intervals
Even and odd functions are particularly useful in calculating definite integrals over intervals symmetric with respect to the origin.
If \( f \) is even, then:
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
If \( f \) is odd, then:
\[ \int_{-a}^{a} f(x) \, dx = 0 \]
Decomposition of a function into even and odd parts
Let \( f : X \to \mathbb{R} \) be a function defined on a set symmetric with respect to the origin, that is such that \( x \in X \implies -x \in X \). In this case, the function \( f \) can be written uniquely as the sum of an even function and an odd function.
Precisely, we define:
\[ f_p(x) = \frac{f(x) + f(-x)}{2} \quad \text{(even part of \( f \))} \]
\[ f_d(x) = \frac{f(x) - f(-x)}{2} \quad \text{(odd part of \( f \))} \]
It is immediate to verify that \( f_p(-x) = f_p(x) \) and \( f_d(-x) = -f_d(x) \), therefore \( f_p \) is even and \( f_d \) is odd. Moreover, adding the two expressions we obtain:
\[ f(x) = f_p(x) + f_d(x) \]
that is, every function \( f \) (defined on a symmetric set) can be uniquely decomposed into the sum of an even function and an odd function.
Example. Consider the function \( f(x) = e^x \), defined on all of \( \mathbb{R} \). The even part is:
\[ f_p(x) = \frac{e^x + e^{-x}}{2} = \cosh x \]
while the odd part is:
\[ f_d(x) = \frac{e^x - e^{-x}}{2} = \sinh x \]
We thus have the decomposition:
\[ e^x = \cosh x + \sinh x \]
Remark: The decomposition is possible only if the domain of the function is symmetric with respect to the origin. Moreover, the expression \( f = f_p + f_d \) is unique: there exists exactly one even function and one odd function whose sum gives \( f \).
Proof of uniqueness of decomposition
Suppose that a function \( f : X \to \mathbb{R} \), defined on a set symmetric with respect to the origin, can be written in two distinct ways as the sum of an even function and an odd function:
\[ f(x) = f_p(x) + f_d(x) = g_p(x) + g_d(x), \]
where \( f_p \), \( g_p \) are even and \( f_d \), \( g_d \) are odd.
Then:
\[ f_p(x) - g_p(x) = g_d(x) - f_d(x) \]
Let us call \( h(x) = f_p(x) - g_p(x) = g_d(x) - f_d(x) \). The function \( h \) is therefore even (as the difference of two even functions) and odd (as the difference of two odd functions).
But if a function is simultaneously even and odd, then:
\[ h(x) = h(-x) \quad \text{and} \quad h(x) = -h(-x) \implies h(x) = -h(x) \]
that is \( h(x) = 0 \) for every \( x \in X \).
Therefore \( f_p(x) = g_p(x) \) and \( f_d(x) = g_d(x) \), which proves the uniqueness of the decomposition.

