The study of the relative positions of two lines is one of the fundamental topics in plane analytic geometry. Understanding how two lines can be positioned in the Cartesian plane allows us to accurately classify all possible geometric situations: from intersection at a single point to complete superposition.
Table of Contents
- Representation of lines in the plane
- Classification of relative positions
- Perpendicular lines
- Solved exercises
Representation of lines in the plane
Given two lines in the plane, three main configurations can occur:
- Coincident lines: these are two equations that actually describe the same line. In this case, the lines have all points in common and are geometrically indistinguishable.
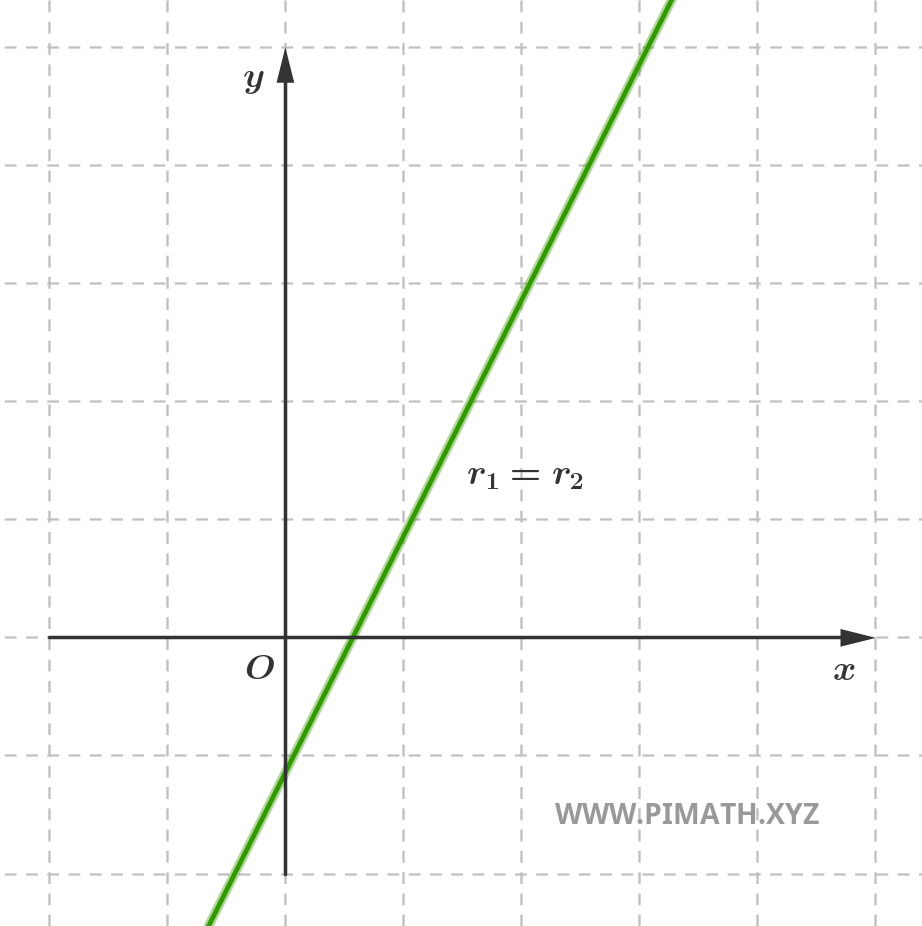
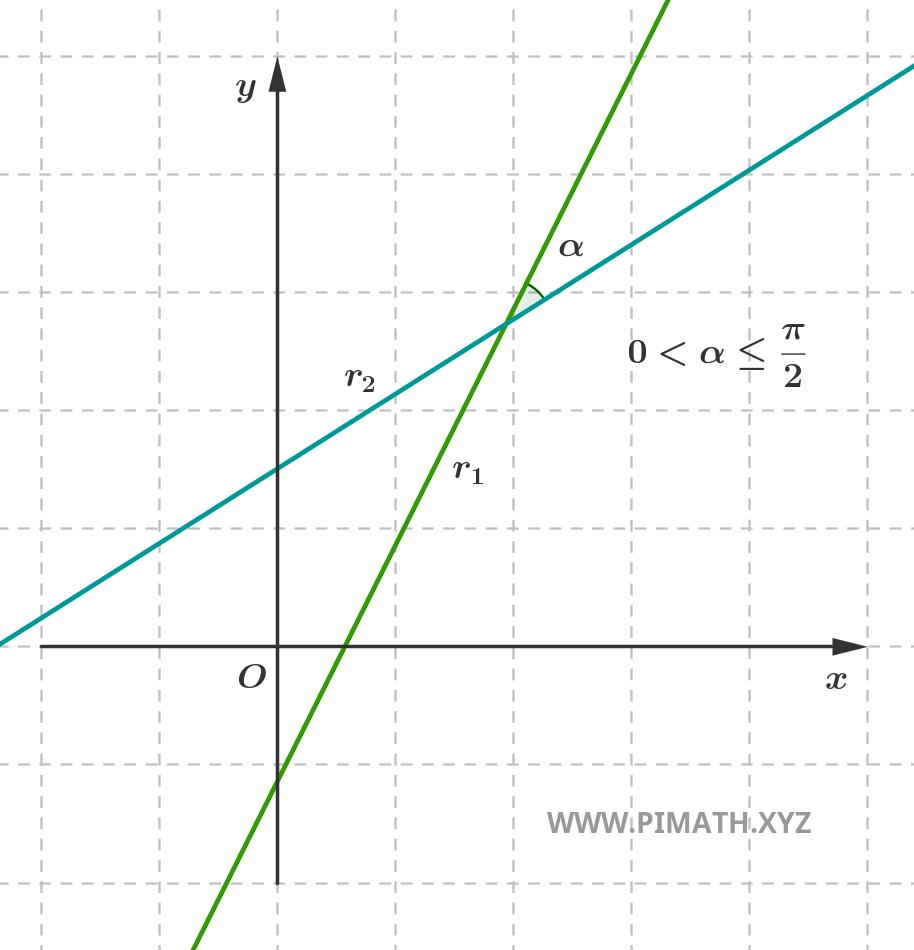
- Intersecting lines: they intersect at a single point in the plane, forming an angle that can take any amplitude between 0° and 180°, excluding cases of parallelism.
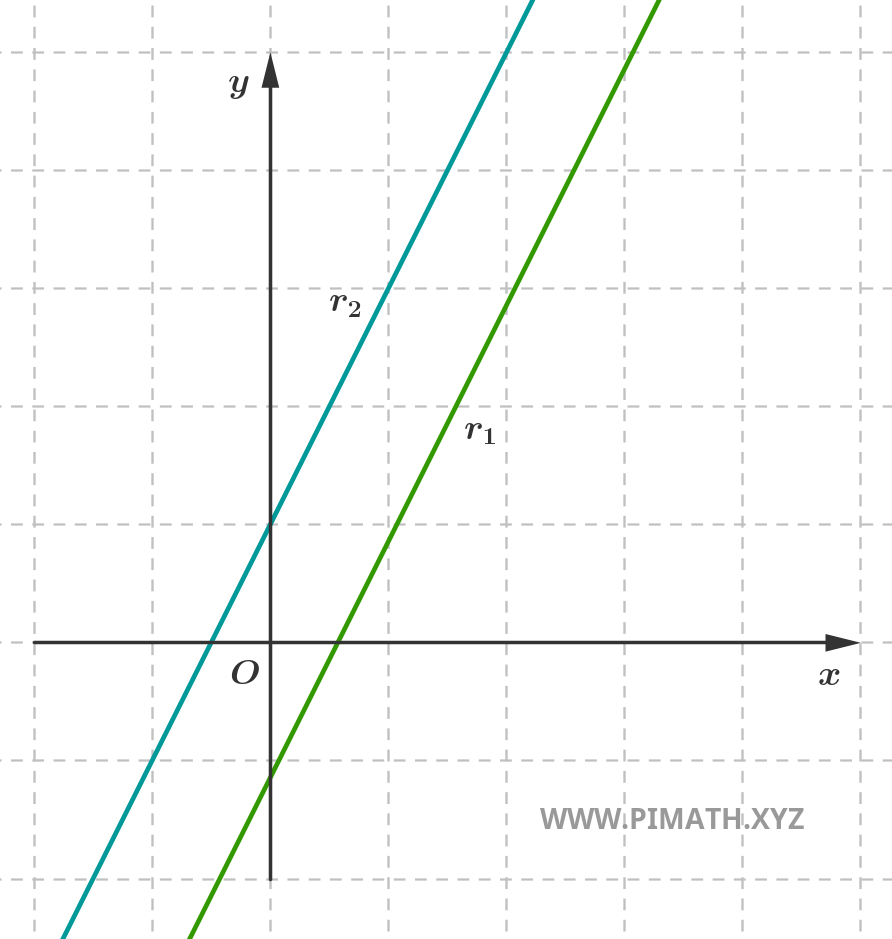
- Distinct parallel lines: although they have the same inclination (i.e., the same slope), these lines never meet. They share no points.
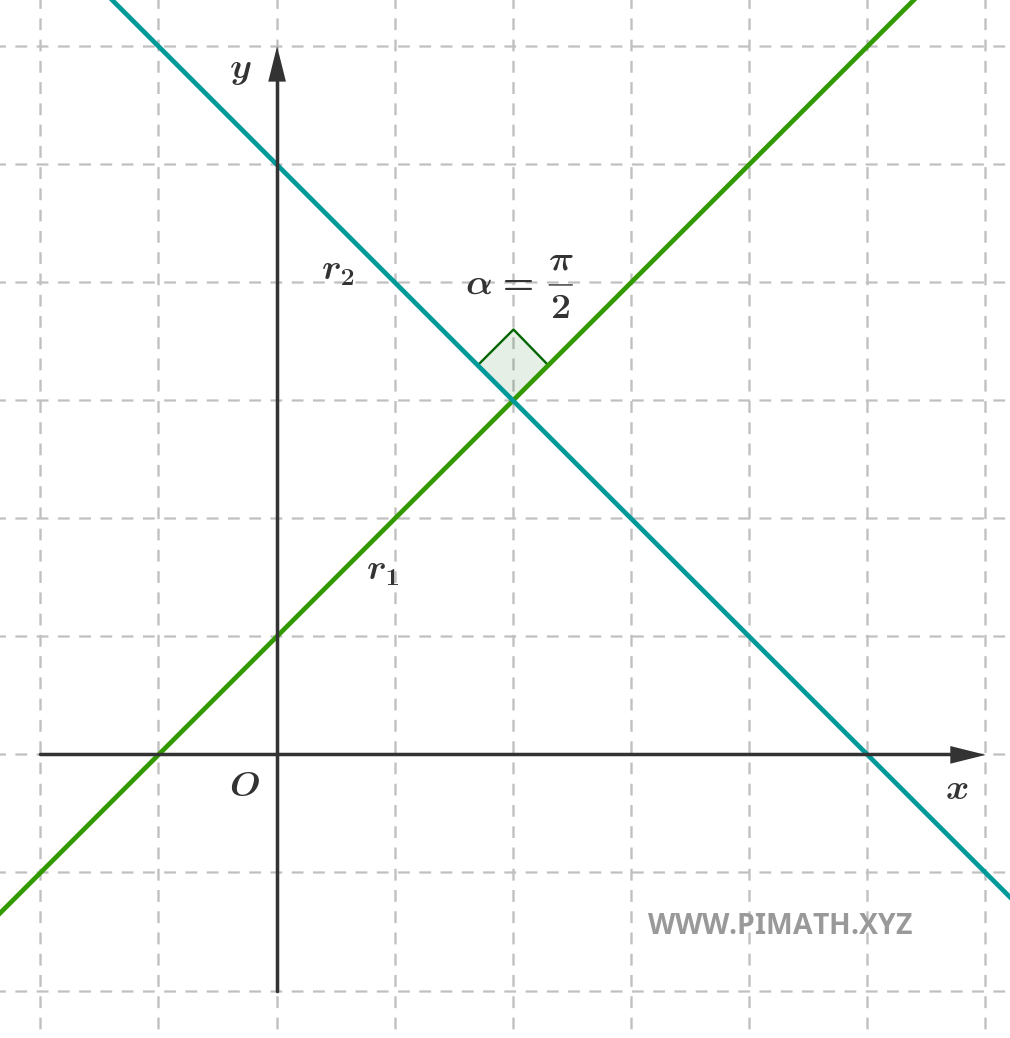
Within intersecting lines lies a very important special case: that of perpendicular lines. Two lines are perpendicular if they intersect forming a right angle \( \displaystyle \frac{\pi}{2} \) (i.e., 90°).
Forms of the equation of a line
A line in the Cartesian plane can be represented in multiple ways, equivalent to each other but useful in different contexts.
The explicit form, also called slope-intercept form, is perhaps the most intuitive:
\[ y = mx + b \]
In this equation:
The parameter \( m \in \mathbb{R} \) is called the slope and represents the inclination of the line. By convention, if the line is vertical, we say that the slope is infinite or undefined.
The term \( b \in \mathbb{R} \) is the y-intercept, i.e., the point where the line intersects the \( y \)-axis.
Another way of writing is the implicit form, also called general form:
\[ ax + by + c = 0 \]
In this case, \( a, b, c \in \mathbb{R} \), and we must have \( a^2 + b^2 \neq 0 \) for this to actually be the equation of a line.
Relationship between the forms
When the coefficient \( b \) is different from zero, it is possible to derive the explicit form from the implicit form. Indeed, solving for \( y \), we get:
\[ ax + by + c = 0 \quad \Leftrightarrow \quad y = -\frac{a}{b}x - \frac{c}{b} \]
In this way, the slope is \( m = -\displaystyle \frac{a}{b} \) and the y-intercept is \( b = -\displaystyle \frac{c}{b} \).
If instead \( b = 0 \) and \( a \neq 0 \), the equation reduces to the form \( x = -\displaystyle \frac{c}{a} \), which represents a vertical line. In this case, the slope is undefined.
Classification of relative positions
Coincident lines
Two lines are coincident when they coincide point by point: each point of one also belongs to the other. Essentially, it is the same line expressed with two proportional equations.
If they are expressed in explicit form, we have:
\[ r: y = mx + b \quad \text{and} \quad s: y = mx + b \]
In implicit form, two lines \( r: a_1x + b_1y + c_1 = 0 \) and \( s: a_2x + b_2y + c_2 = 0 \) are coincident if and only if there exists a constant \( k \neq 0 \) such that:
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} = k \]
Equivalently, this means that \( (a_2, b_2, c_2) = k(a_1, b_1, c_1) \) for some \( k \neq 0 \).
Example: the lines \( 2x + 3y - 6 = 0 \) and \( 4x + 6y - 12 = 0 \) are coincident, because the coefficients of one are double those of the other:
\[ \frac{2}{4} = \frac{3}{6} = \frac{-6}{-12} = \frac{1}{2} \]
Parallel lines
Two lines are parallel if they have the same direction. In the case where they do not coincide, they are called distinct parallel lines and have no points in common.
In explicit form, the condition for parallelism is:
\[ m_1 = m_2 \]
If also \( b_1 \neq b_2 \), then the lines are distinct parallel lines.
In implicit form, two lines \( r: a_1x + b_1y + c_1 = 0 \) and \( s: a_2x + b_2y + c_2 = 0 \) are parallel if and only if:
\[ a_1b_2 - a_2b_1 = 0 \]
This is equivalent to saying that \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \) (when \( a_2, b_2 \neq 0 \)).
To have distinct parallelism, we must also verify that:
\[ \frac{c_1}{c_2} \neq \frac{a_1}{a_2} \quad \text{(i.e.,} \quad \frac{c_1}{c_2} \neq \frac{b_1}{b_2}\text{)} \]
Example: the lines \( r: y = 3x + 2 \) and \( s: y = 3x - 1 \) are distinct parallel lines because they have the same slope but different y-intercepts.
Intersecting lines
Two lines are intersecting if they intersect at a single point. This occurs when the lines have different directions, i.e., distinct slopes (in the case of non-vertical lines).
In explicit form, it suffices to verify that:
\[ m_1 \neq m_2 \]
In implicit form, the condition is:
\[ a_1b_2 - a_2b_1 \neq 0 \]
Point of intersection
To determine the point of intersection between two intersecting lines expressed in implicit form, we solve the following linear system:
\[ \begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0 \end{cases} \]
Applying Cramer's rule, the coordinates of the intersection point are:
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]
provided that \( a_1b_2 - a_2b_1 \neq 0 \).
Perpendicular lines
Condition for perpendicularity
Two lines are perpendicular if they intersect forming a right angle, i.e., 90°.
In explicit form, if the lines have finite slopes \( m_1 \) and \( m_2 \), the condition is:
\[ m_1 \cdot m_2 = -1 \]
Special case: a horizontal line (\( m = 0 \)) is perpendicular to a vertical line (undefined slope).
In implicit form, two lines \( r: a_1x + b_1y + c_1 = 0 \) and \( s: a_2x + b_2y + c_2 = 0 \) are perpendicular if and only if:
\[ a_1a_2 + b_1b_2 = 0 \]
This relationship derives from the fact that the normal vectors of the two lines, \( \vec{n}_1 = (a_1, b_1) \) and \( \vec{n}_2 = (a_2, b_2) \), are orthogonal, i.e., their dot product is zero.
Analytical proof
The angle \( \theta \) between two lines with slopes \( m_1 \) and \( m_2 \) is expressed by the formula:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]
where \( \theta \) represents the acute angle between the two lines.
If \( m_1m_2 = -1 \), the denominator \( 1 + m_1m_2 \) becomes zero and the tangent becomes undefined, which corresponds to a 90° angle.
Solved exercises
Exercise 1. Determine whether the lines \( r: y = -2x + 1 \) and \( s: y = \displaystyle \frac{1}{2}x - 3 \) are perpendicular.
Let's determine the slopes:
\[ m_1 = -2 \]
\[ m_2 = \frac{1}{2} \]
Let's verify the product of the two coefficients:
\[ m_1 \cdot m_2 = (-2) \cdot \frac{1}{2} = -1 \]
Since the product equals -1, we can conclude that the two lines are perpendicular.
Exercise 2. Calculate the acute angle between the lines \( r: y = 2x \) and \( s: y = -x \).
The slopes are:
\[ m_1 = 2 \]
\[ m_2 = -1 \]
Let's use the formula for calculating the acute angle \( \theta \) between two lines:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right| = \left| \frac{-1 - 2}{1 + 2 \cdot (-1)} \right| = \left| \frac{-3}{1 - 2} \right| = \left| \frac{-3}{-1} \right| = 3 \]
Therefore:
\[ \theta = \arctan(3) \approx 71{.}57^\circ \]
Exercise 3. Find the equation of the line perpendicular to \( r: y = -\displaystyle \frac{3}{2}x + 4 \) and passing through the point \( P(2, 1) \).
The slope of the given line is \( m = -\displaystyle \frac{3}{2} \).
The slope of the perpendicular line will be the negative reciprocal:
\[ m' = -\frac{1}{m} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3} \]
Let's use the point-slope formula for lines passing through \( P(2, 1) \):
\[ y - y_0 = m'(x - x_0) \quad \text{with } (x_0, y_0) = (2, 1) \] \[ y - 1 = \frac{2}{3}(x - 2) \] \[ y = \frac{2}{3}x - \frac{4}{3} + 1 = \frac{2}{3}x - \frac{1}{3} \]
The desired equation is:
\[ y = \frac{2}{3}x - \frac{1}{3} \]
Exercise 4. Determine the value of \( k \) so that the lines \( r: 2x + 3y - 1 = 0 \) and \( s: kx + 6y + 2 = 0 \) are parallel.
Two lines in implicit form are parallel if \( a_1b_2 - a_2b_1 = 0 \).
Let's identify the coefficients:
- Line \( r \): \( a_1 = 2, b_1 = 3, c_1 = -1 \)
- Line \( s \): \( a_2 = k, b_2 = 6, c_2 = 2 \)
Let's apply the condition:
\[ a_1b_2 - a_2b_1 = 2 \cdot 6 - k \cdot 3 = 12 - 3k = 0 \] \[ 3k = 12 \quad \Rightarrow \quad k = 4 \]
Let's verify that for \( k = 4 \) the lines are indeed distinct parallel lines:
\[ \frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \]
\[ \frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2} \]
\[ \frac{c_1}{c_2} = \frac{-1}{2} = -\frac{1}{2} \]
Since \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \neq \displaystyle \frac{c_1}{c_2} \), the lines are distinct parallel lines for \( k = 4 \).
Exercise 5. Determine the point of intersection between the lines:
\( r: x + 2y - 3 = 0 \)
\( s: 2x - y + 1 = 0 \)
Let's solve the system:
\[ \begin{cases} x + 2y = 3 \\ 2x - y = -1 \end{cases} \]
Let's use the elimination method. Multiply the second equation by 2:
\[ \begin{cases} x + 2y = 3 \\ 4x - 2y = -2 \end{cases} \]
Add the two equations:
\[ x + 4x + 2y - 2y = 3 + (-2) \] \[ 5x = 1 \quad \Rightarrow \quad x = \frac{1}{5} \]
Substitute into the first equation:
\[ \frac{1}{5} + 2y = 3 \quad \Rightarrow \quad 2y = 3 - \frac{1}{5} = \frac{15 - 1}{5} = \frac{14}{5} \] \[ y = \frac{7}{5} \]
The point of intersection is:
\[ \left( \frac{1}{5}, \frac{7}{5} \right) \]
Verification: substituting into both original equations yields the identity \( 0 = 0 \), confirming the correctness of the result.

