La elipse es el lugar geométrico de los puntos del plano para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante. Tiene dos ejes de simetría, llamados eje mayor y eje menor. Es una curva cerrada y simétrica, con numerosas aplicaciones en física y geometría.
Índice
- Cómo encontrar la ecuación canónica de la elipse
- Elipse con Semieje Mayor en el Eje de Ordenadas
- Cómo Encontrar la Ecuación de la Elipse Trasladada
- Relación entre los parámetros de la elipse
- Excentricidad de la Elipse: Definición, Significado Geométrico y Fórmula
- Ejercicios Resueltos
Denotemos los dos focos como \( F_1(-c, 0) \) y \( F_2(c, 0) \), y sea \( P(x, y) \) cualquier punto perteneciente a la elipse. Entonces se cumple la siguiente relación:
\[ |PF_1| + |PF_2| = 2a \]
La constante \( 2a \) – que representa la suma de las distancias \( |PF_1|\) y \(|PF_2|\) – es siempre mayor que la distancia entre los dos focos, \( 2c \). Este concepto se ilustra en la siguiente figura:
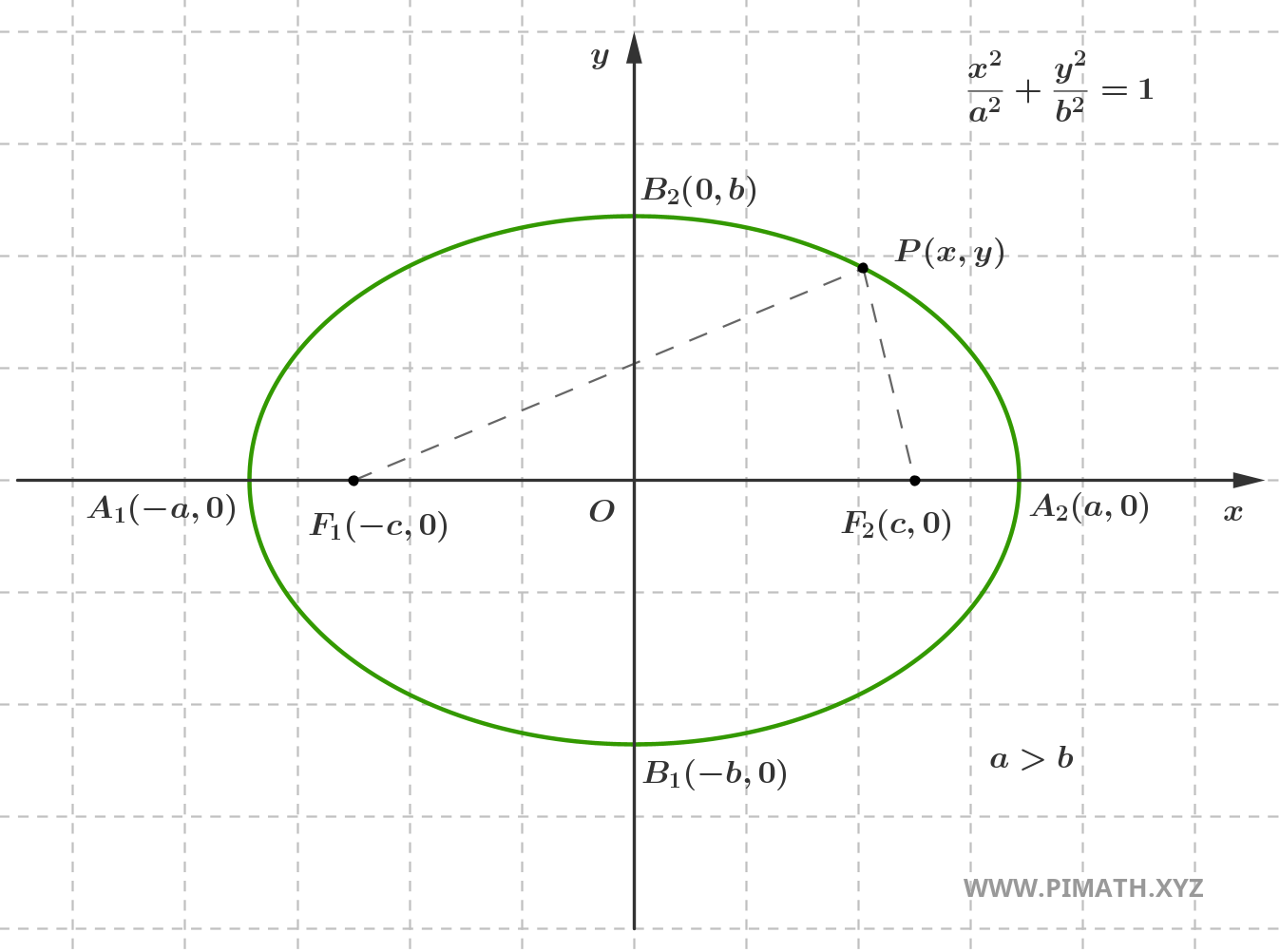
En la imagen, el segmento que conecta el centro \( O \) con el punto \( A_2 \) en el eje horizontal se llama semieje mayor, y su longitud es exactamente \( a \). El segmento vertical que conecta el centro con el punto \( B_2 \) se llama semieje menor y tiene longitud \( b \).
La relación que define la elipse debe cumplirse naturalmente para todos los puntos de la elipse. Consideremos el caso particular en el que el punto \( P(x,y) \) coincide con el punto \( B_2(0,b) \):
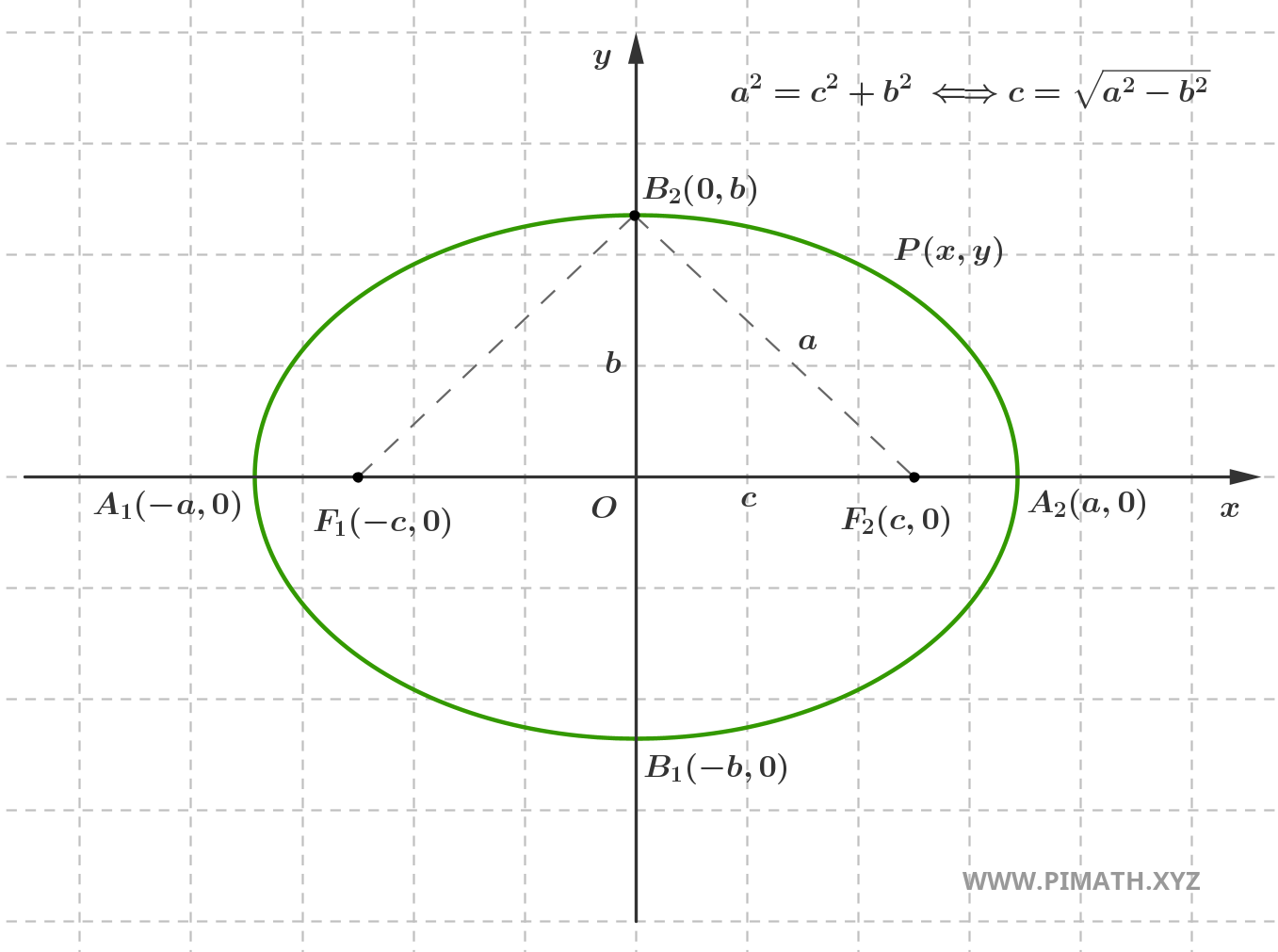
Considerando el triángulo rectángulo con vértices \( O(0,0) \), \( F_2(c,0) \) y \( B_2(0,b) \) y aplicando el Teorema de Pitágoras, se obtiene que \( c=\sqrt{a^2-b^2} \), como se muestra en la figura.
Cómo encontrar la ecuación canónica de la elipse
Consideremos un caso simplificado en el que el centro de la elipse coincide con el origen del sistema de coordenadas, con los focos ubicados a lo largo del eje horizontal en los puntos \( F_1(-c, 0) \) y \( F_2(c, 0) \).
Consideremos un punto genérico \( P(x, y) \) en el plano. Para que \( P \) pertenezca a la elipse, debe cumplirse la relación:
\[ |PF_1| + |PF_2| = 2a \quad , \quad a > c \]
Ahora calculamos las distancias entre el punto \( P(x, y) \) y cada uno de los dos focos:
\[ |PF_1| = \sqrt{(x + c)^2 + y^2} \quad \text{y} \quad |PF_2| = \sqrt{(x - c)^2 + y^2} \]
Sustituyendo estas expresiones en la condición inicial obtenemos:
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \]
Para eliminar uno de los radicales, pasamos \( \sqrt{(x + c)^2 + y^2} \) al segundo miembro:
\[ \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2} \]
Elevamos al cuadrado ambos miembros para eliminar el radical:
\[ (x - c)^2 + y^2 = \left(2a - \sqrt{(x + c)^2 + y^2} \right)^2 \]
Desarrollamos el cuadrado del segundo miembro:
\[ (x - c)^2 + y^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
Eliminamos el término \( y^2 \) presente en ambos lados y desarrollamos los cuadrados:
\[ x^2 - 2cx + c^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 \]
Simplificando ambos miembros:
\[ -4cx = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} \]
Dividimos ambos miembros por 4:
\[ -cx = a^2 - a\sqrt{(x + c)^2 + y^2} \]
Pasamos todos los términos con el radical al primer miembro:
\[ a\sqrt{(x + c)^2 + y^2} = a^2 + cx \]
Elevamos al cuadrado nuevamente ambos miembros:
\[ a^2[(x + c)^2 + y^2] = (a^2 + cx)^2 \]
Desarrollamos ambos lados:
\[ a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2 \]
Desarrollamos completamente:
\[ a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2 \]
Simplificamos los términos comunes de ambos lados:
\[ a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2 \]
Agrupamos los términos semejantes:
\[ x^2(a^2 - c^2) + a^2y^2 = a^2(a^2 - c^2) \]
Puesto que \( a > c \), la cantidad \( a^2 - c^2 \) es positiva. La denotamos como \( b^2 \), así obtenemos:
\[ b^2 = a^2 - c^2 \]
Sustituyendo, obtenemos:
\[ x^2b^2 + a^2y^2 = a^2b^2 \]
Dividimos ambos miembros por \( a^2b^2 \) para aislar los términos:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , \quad a > b \]
Esta es la forma canónica de la ecuación de la elipse con centro en el origen y focos en el eje de abscisas. La ecuación es simétrica respecto a ambos ejes cartesianos y respecto al origen.
Introduzcamos algo de nomenclatura. La recta que contiene los focos se llama eje focal, mientras que el punto de intersección entre los ejes es el centro de la elipse.
- Los puntos en los que la elipse interseca el eje focal y la recta perpendicular a él que pasa por el centro se llaman vértices de la elipse.
- El segmento \( A_1A_2 \) se llama eje mayor, mientras que el segmento \( B_1B_2 \) se llama eje menor.
- Se define semieje mayor la longitud \( a \), y semieje menor la longitud \( b \).
Elipse con Semieje Mayor en el Eje de Ordenadas
Si queremos describir una elipse que tiene el semieje mayor vertical, es decir, orientado a lo largo del eje de ordenadas, simplemente necesitamos intercambiar los roles de \( a \) y \( b \) en la ecuación canónica que describe la elipse con semieje mayor en el eje de abscisas, como se muestra en la figura:
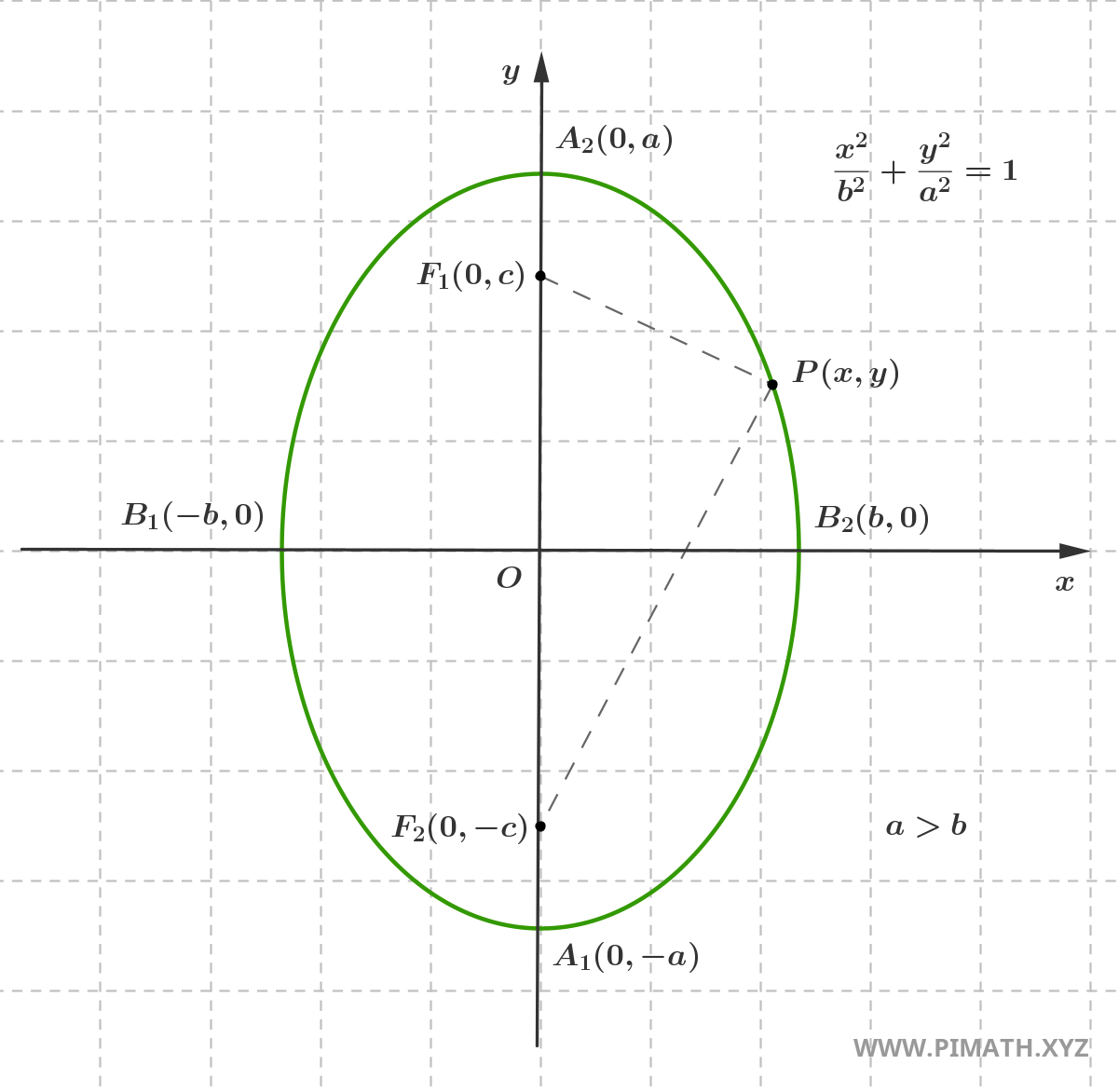
En este caso, imponiendo \( |PF_1| + |PF_2| = 2a \) y con pasos algebraicos análogos, la ecuación de la elipse se convierte en:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \]
Este cambio refleja una rotación de la elipse de 90 grados respecto al eje x. La forma de la ecuación permanece igual, pero cambia el eje a lo largo del cual se extiende la elipse.
También en este caso el centro de la elipse permanece en el origen y la definición geométrica sigue siendo válida: para cada punto \( P(x, y) \) en la elipse, la suma de las distancias a los focos (que ahora están ubicados a lo largo del eje y) es siempre igual a \( 2a \).
Cómo Encontrar la Ecuación de la Elipse Trasladada
Hasta ahora hemos considerado una elipse con centro en el origen y focos en el eje de abscisas. Sin embargo, una elipse puede encontrarse en cualquier punto del plano. En tal caso, se habla de elipse trasladada.
Supongamos que el centro de la elipse está en el punto \( C(x_0, y_0) \). La ecuación canónica se modifica en consecuencia, trasladando las coordenadas.
Para la ecuación de la elipse trasladada, es fundamental distinguir cuál es el semieje mayor y cuál el semieje menor. Dependiendo de la orientación de la elipse respecto a los ejes cartesianos, la ecuación canónica trasladada toma formas ligeramente diferentes:
Elipse Trasladada Horizontal
El eje mayor es paralelo al eje x, por lo que los focos están a lo largo de la recta \( y = y_0 \)
En este caso, el semieje mayor \( a \) es el valor bajo el término \( (x - x_0)^2 \), y el semieje menor \( b \) es el valor bajo el término \( (y - y_0)^2 \).
\[ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 \quad , \quad a > b \]
Elipse Trasladada Vertical
El eje mayor es paralelo al eje y, por lo que los focos están a lo largo de la recta \( x = x_0 \)
En este caso, el semieje mayor \( a \) es el valor bajo el término \( (y - y_0)^2 \), y el semieje menor \( b \) es el valor bajo el término \( (x - x_0)^2 \).
\[ \frac{(x - x_0)^2}{b^2} + \frac{(y - y_0)^2}{a^2} = 1 \quad , \quad a > b \]
Nota: Los focos ya no se encuentran en los ejes cartesianos x o y, sino en rectas paralelas a estos, que pasan por el centro \( (x_0, y_0) \).
Relación entre los parámetros de la elipse
En el caso de una elipse con centro en el origen y ejes paralelos a los ejes cartesianos, la relación entre los parámetros principales está dada por una fórmula fundamental que conecta el semieje mayor \( a \), el semieje menor \( b \) y la distancia de los focos al centro \( c \).
La fórmula es la siguiente:
\[ c^2 = a^2 - b^2 \]
Por lo tanto, la distancia de los focos al centro se puede calcular como:
\[ c = \sqrt{a^2 - b^2} \]
Esta relación es válida para todas las elipses con centro en el origen y ejes alineados con los ejes cartesianos, donde \( a > b \). El semieje mayor siempre está asociado con el eje que tiene el denominador más grande en la ecuación canónica de la elipse:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , a > b \quad \text{(si el eje mayor es horizontal)} \]
En cambio:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \quad \text{(si el eje mayor es vertical)} \]
En este caso, \( c^2 = a^2 - b^2 \) y por tanto \( c = \sqrt{a^2 - b^2} \). Conocer estas relaciones permite calcular rápidamente la posición de los focos y comprender mejor la geometría de la elipse.
Excentricidad de la Elipse: Definición, Significado Geométrico y Fórmula
La excentricidad es una medida fundamental que nos permite entender cuánto se desvía una elipse de ser un círculo. Cada elipse tiene dos focos: son dos puntos interiores tales que la suma de las distancias desde cualquier punto de la elipse a los dos focos es constante. La excentricidad, indicada con la letra \( e \), es un número que varía de \( 0 \) a \( 1 \) y describe la forma de la elipse.
Definición de Excentricidad
La excentricidad \( e \) no es un dato que se elige arbitrariamente, sino un valor que emerge naturalmente de las propiedades geométricas de la elipse. En particular, si \( a \) es la longitud del semieje mayor y \( b \) la del semieje menor, entonces la distancia \( c \) entre el centro y uno de los focos es: \[c = \sqrt{a^2 - b^2}\] Con \( a > b \), la excentricidad siempre está dada por la siguiente fórmula: \[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1-\frac{b^2}{a^2}}\] Esta fórmula es válida tanto cuando el eje mayor es horizontal como cuando es vertical, ya que \( a \) representa siempre el semieje mayor independientemente de la orientación de la elipse.
Significado Geométrico de la Excentricidad
Cuando la excentricidad es igual a cero, es decir \( e = 0 \), significa que los dos focos coinciden en el centro de la elipse. En este caso la elipse es en realidad una circunferencia, porque todos los radios (es decir, los segmentos que unen el centro con un punto de la curva) tienen la misma longitud: \( a = b \).
Cuando en cambio la excentricidad es un número comprendido entre \( 0 \) y \( 1 \), es decir \( 0 < e < 1 \), la elipse está alargada. Cuanto mayor es el valor de \( e \), más se alejan los focos del centro y más la elipse aparece alargada a lo largo del eje mayor y comprimida a lo largo del eje menor.
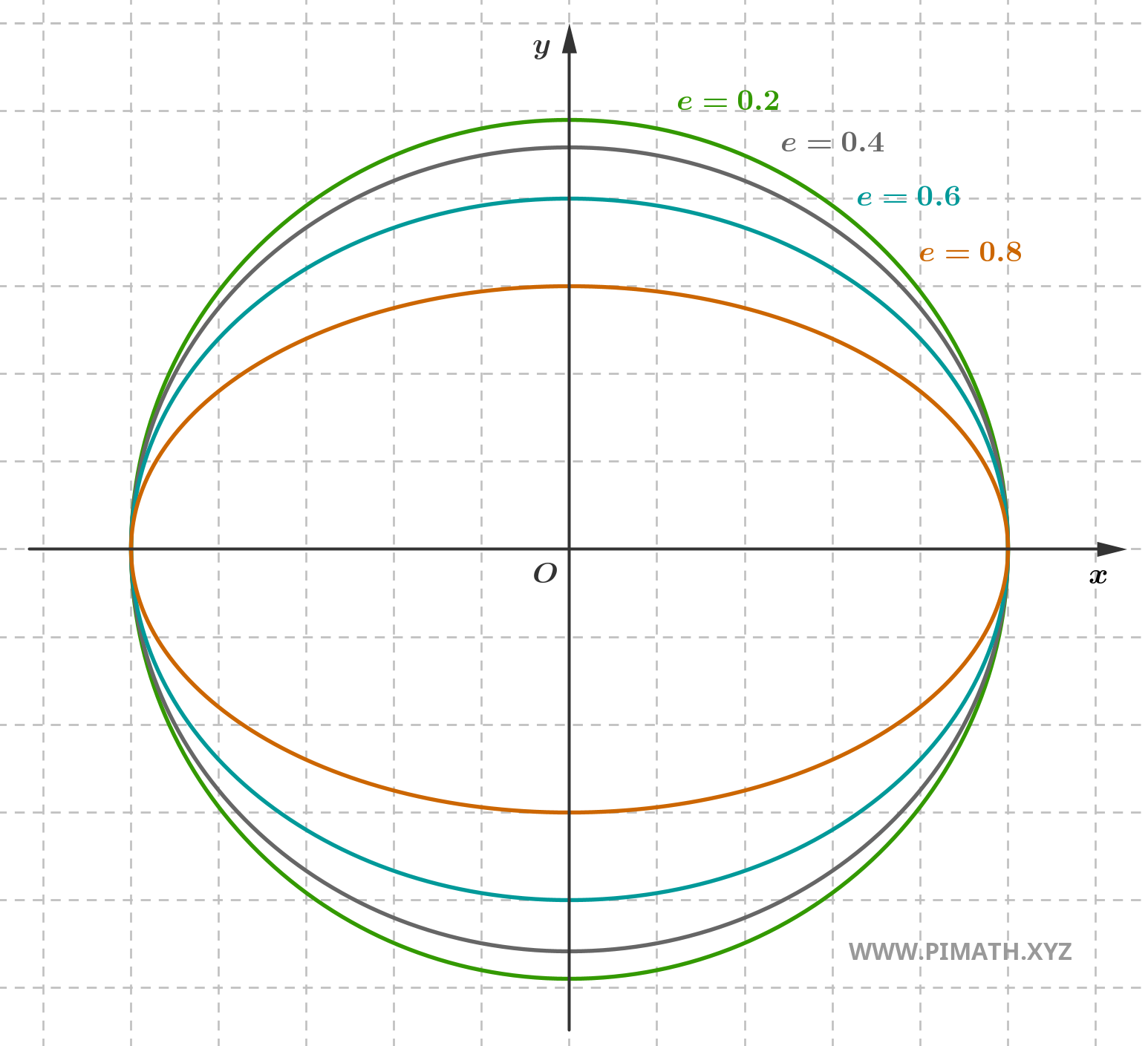
Finalmente, cuando \( e \) se acerca a \( 1 \), la forma de la elipse se vuelve extremadamente alargada y los focos están muy distantes del centro.
Por ejemplo, consideremos una elipse con semieje mayor \( a = 5 \) y semieje menor \( b = 3 \).
Calculamos primero la distancia de los focos al centro:
\[c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4\]
En este punto podemos calcular la excentricidad:
\[e = \frac{4}{5} = 0{,}8\]
El valor que hemos encontrado indica que la elipse está bastante achatada y los focos están bien separados del centro. Aquí está el gráfico:
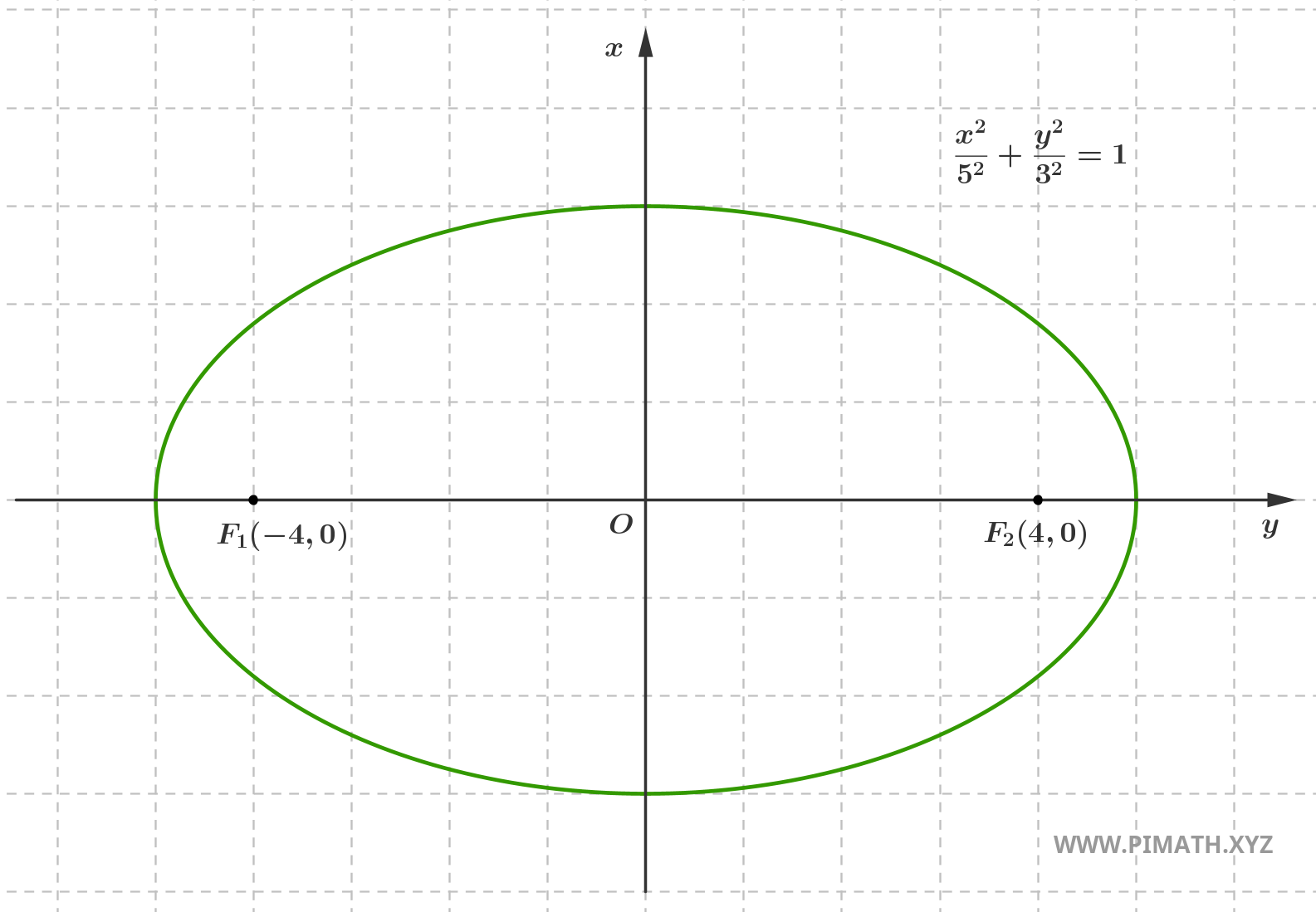
La excentricidad de la elipse es un concepto que relaciona la posición de los focos con la forma general de la curva. No es solo una fórmula para memorizar, sino una herramienta útil para intuir visualmente qué tan cerca está la elipse de un círculo o qué tan alargada está. Recuerda: cuanto más cerca esté \( e \) de cero, más se parece la elipse a un círculo. Cuanto más cerca esté \( e \) de \( 1 \), más achatada está y más lejos están los focos.
Ejercicios Resueltos
Ejercicio 1. Verificar si el punto \( P(3, 2) \) pertenece a la elipse de ecuación:
\[ \frac{x^2}{9} + \frac{y^2}{4} = 1 \]
Solución. Sustituimos \( x = 3 \), \( y = 2 \):
\[ \frac{3^2}{9} + \frac{2^2}{4} = \frac{9}{9} + \frac{4}{4} = 1 + 1 = 2 \neq 1 \]
Esto significa que el punto no pertenece a la elipse.
Ejercicio 2. Una elipse tiene centro en el origen, eje mayor horizontal, semieje mayor \( a = 5 \) y semieje menor \( b = 3 \). Encontrar la ecuación de la elipse.
Solución. La ecuación canónica es
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{9} = 1 \]
Ejercicio 3. Determina la posición de los focos de la elipse de ecuación:
\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]
Encontrar la distancia de los focos \( c \).
Solución. De la ecuación \( \displaystyle \frac{x^2}{16} + \displaystyle \frac{y^2}{9} = 1 \), identificamos que el término mayor (16) está bajo \( x^2 \), por lo que el eje mayor es horizontal.
Según nuestra convención: \( a^2 = 16 \), \( b^2 = 9 \), por lo tanto \( a = 4 \), \( b = 3 \).
Calculamos la distancia de los focos \( c \) usando:
\[ c^2 = a^2 - b^2 = 16 - 9 = 7 \Rightarrow c = \sqrt{7} \]
Los focos se encuentran en los puntos \( F_1(-\sqrt{7}, 0) \), \( F_2(\sqrt{7}, 0) \).
Ejercicio 4. Escribe la ecuación canónica de la elipse con centro en el origen, eje mayor vertical, sabiendo que los vértices se encuentran en los puntos \( (0, \pm 6) \) y los focos se encuentran en los puntos \( (0, \pm 4) \).
Solución. Si los vértices están en \( (0, \pm 6) \), entonces el semieje mayor es \( a = 6 \), por lo tanto \( a^2 = 36 \).
Los focos están en \( (0, \pm 4) \), por lo tanto \( c = 4 \), por lo tanto \( c^2 = 16 \).
Calculamos:
\[ b^2 = a^2 - c^2 = 36 - 16 = 20 \]
La ecuación de la elipse, con eje mayor vertical, es: \[ \displaystyle \frac{x^2}{b^2} + \displaystyle \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{20} + \frac{y^2}{36} = 1 \]
Ejercicio 5. Una elipse tiene los focos en los puntos \( F_1(-3,0) \) y \( F_2(3,0) \), y pasa por el punto \( P(4,1) \). Encuentra la ecuación canónica de la elipse.
Solución. Los focos son \( F_1(-3, 0) \), \( F_2(3, 0) \). Entonces \( c = 3 \), por lo tanto \( c^2 = 9 \).
El punto \( P(4, 1) \) pertenece a la elipse. Por definición: \[ |PF_1| + |PF_2| = 2a \] Calculamos: \[ |PF_1| = \sqrt{(4 - (-3))^2 + (1 - 0)^2} = \sqrt{7^2 + 1^2} = \sqrt{49 + 1} = \sqrt{50} = 5\sqrt{2} \] \[ |PF_2| = \sqrt{(4 - 3)^2 + (1 - 0)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \] \[ \Rightarrow |PF_1| + |PF_2| = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \] \[ \Rightarrow 2a = 6\sqrt{2} \Rightarrow a = 3\sqrt{2} \Rightarrow a^2 = (3\sqrt{2})^2 = 9 \cdot 2 = 18 \] \[ b^2 = a^2 - c^2 = 18 - 9 = 9 \] La ecuación de la elipse es por lo tanto: \[ \frac{x^2}{18} + \frac{y^2}{9} = 1 \]

