La parábola es el lugar geométrico de los puntos del plano para los cuales la distancia a un punto fijo (foco) es igual a la distancia a una recta fija (directriz). Tiene un eje de simetría que pasa por el foco y es perpendicular a la directriz. Es una curva abierta y simétrica respecto a su propio eje, con numerosas aplicaciones en física y geometría.
Índice
- Ecuación Canónica de la Parábola
- Ecuación Canónica de una Parábola con Eje Vertical u Horizontal
- Parábola Trasladada en el Plano
- Vértice, Foco, Directriz y Ejes de Simetría
- Ecuación de la Parábola Conocidos el Vértice y un Punto
- Ejercicios Resueltos sobre la Parábola
Ecuación Canónica de la Parábola
Una parábola es el lugar geométrico de los puntos \( P(x, y) \) del plano que tienen la misma distancia a un punto fijo, llamado foco, y a una recta fija, llamada directriz.
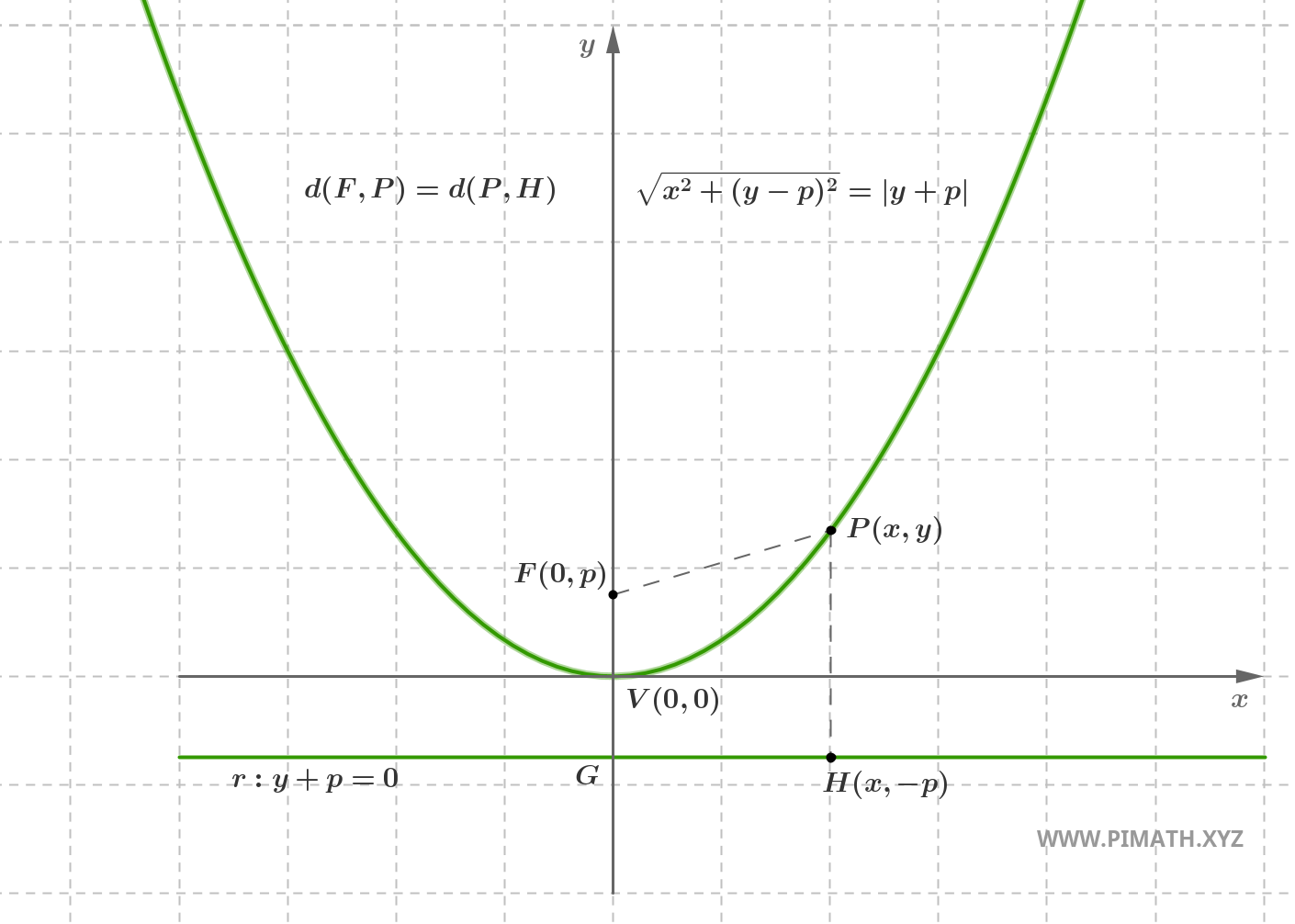
Sea \( F(0, p) \) con \( p > 0 \) el foco y sea \( r \) la directriz, de ecuación \( y = -p \). Por definición, los puntos \( P(x, y) \) de la parábola satisfacen:
\[ \text{d}(P, F) = \text{d}(P, r) \]
Calculamos la distancia entre \( P(x, y) \) y el foco \( F(0, p) \):
\[ \text{d}(P, F) = \sqrt{(x - 0)^2 + (y - p)^2} = \sqrt{x^2 + (y - p)^2} \]
Ahora, calculamos la distancia entre \( P(x, y) \) y la recta directriz \( y = -p \):
\[ \text{d}(P, r) = |y - (-p)| = |y + p| \]
Finalmente, imponemos la igualdad entre las dos distancias:
\[ \sqrt{x^2 + (y - p)^2} = |y + p| \]
Observación: puesto que la parábola se encuentra por encima de la directriz (dado que el foco está por encima de la directriz para \( p > 0 \)), todos los puntos de la parábola satisfacen \( y \geq -p \). Por tanto \( y + p \geq 0 \) y podemos quitar el valor absoluto:
\[ \sqrt{x^2 + (y - p)^2} = y + p \]
Elevamos al cuadrado ambos miembros:
\[ x^2 + (y - p)^2 = (y + p)^2 \]
Desarrollamos los cuadrados:
\[ x^2 + y^2 - 2py + p^2 = y^2 + 2py + p^2 \]
Simplificamos ambos lados:
\[ x^2 - 2py = 2py \]
Llevamos todo al segundo miembro:
\[ x^2 = 4py \]
Finalmente, dividimos por \( 4p \):
\[ y = \frac{1}{4p}x^2 \]
Si ponemos \( a = \displaystyle \frac{1}{4p} \), obtenemos la forma más compacta:
\[ y = ax^2 \]
que es la ecuación canónica de la parábola con vértice en el origen \( V(0, 0) \), foco en \( F(0, p) \) y directriz \( y = -p \).
En resumen, la parábola de ecuación \( y = ax^2 \) tiene eje de simetría vertical, coincidente con el eje \( y \), y la concavidad dirigida hacia arriba si \( a > 0 \), o hacia abajo si \( a < 0 \).
Ecuación Canónica de una Parábola con Eje Vertical u Horizontal
La ecuación canónica de la parábola asume formas diferentes según la orientación del eje de simetría. Distinguimos dos casos fundamentales según el eje sea vertical u horizontal.
Parábola con Eje Vertical
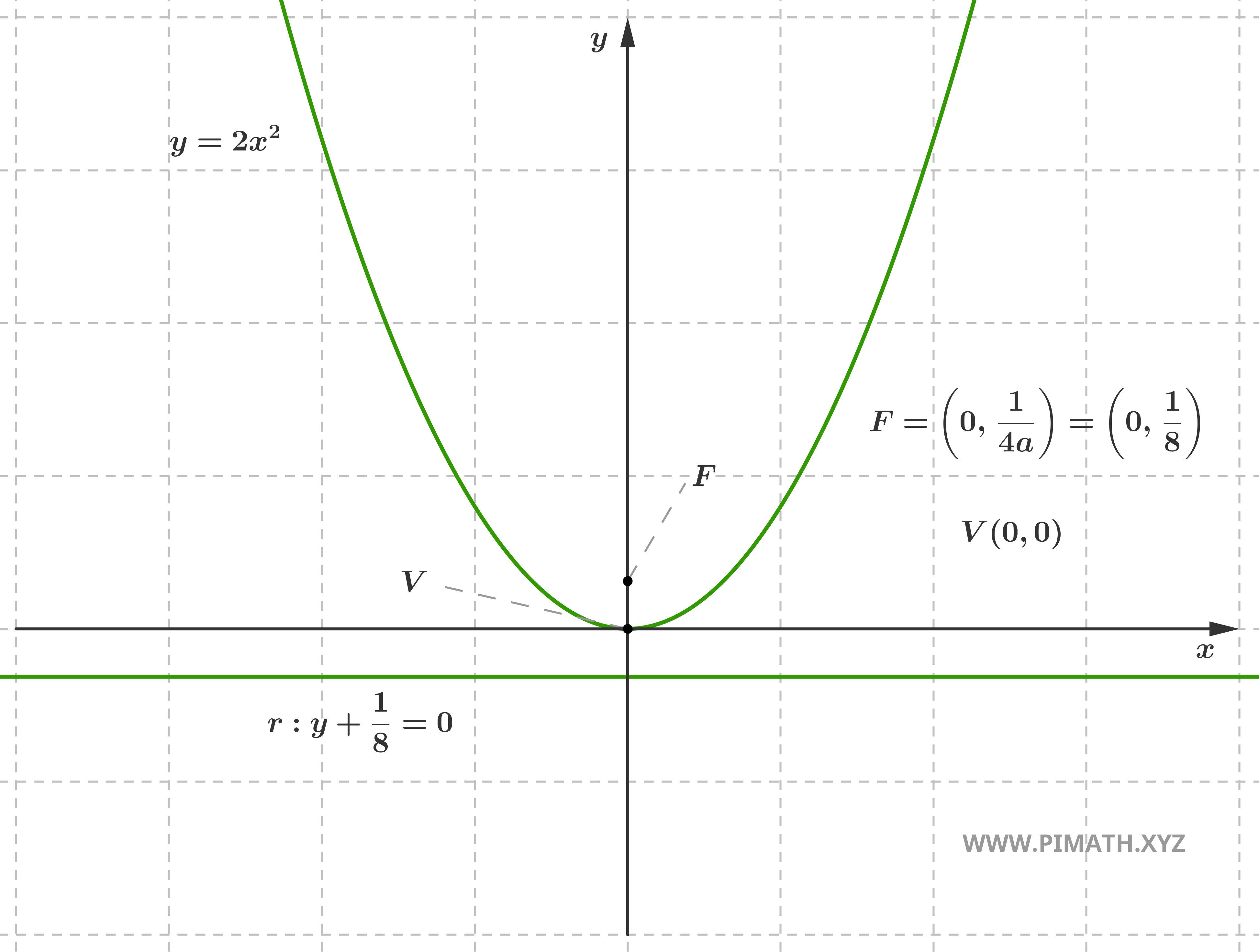
Para una parábola con eje de simetría vertical, paralelo al eje de las ordenadas, la ecuación canónica es \( y = ax^2 \) o, en la forma equivalente, \( x^2 = 4py \). En esta configuración, el coeficiente \( a = \displaystyle \frac{1}{4p} \) representa el coeficiente director, mientras que \( p \) es el parámetro focal que indica la distancia del vértice al foco.
Los elementos característicos son: el Vértice: \( V(0, 0) \), el Foco \( F\left(0, \displaystyle \frac{1}{4a}\right) \), la Directriz: \( y = -\displaystyle\frac{1}{4a} \), el Eje de simetría: \( x = 0 \) (eje \( y \)) y la Concavidad: hacia arriba si \( a > 0 \), hacia abajo si \( a < 0 \)
Ejemplo: Consideremos la parábola \( y = 2x^2 \). Aquí \( a = 2 \), por tanto \( p = \displaystyle \frac{1}{4a} = \displaystyle \frac{1}{8} \). El vértice es \( V(0, 0) \), el foco se encuentra en \( F\left(0, \displaystyle \frac{1}{8}\right) \) y la directriz tiene ecuación \( y = -\displaystyle \frac{1}{8} \). Puesto que \( a > 0 \), la parábola presenta concavidad hacia arriba.
Parábola con Eje Horizontal
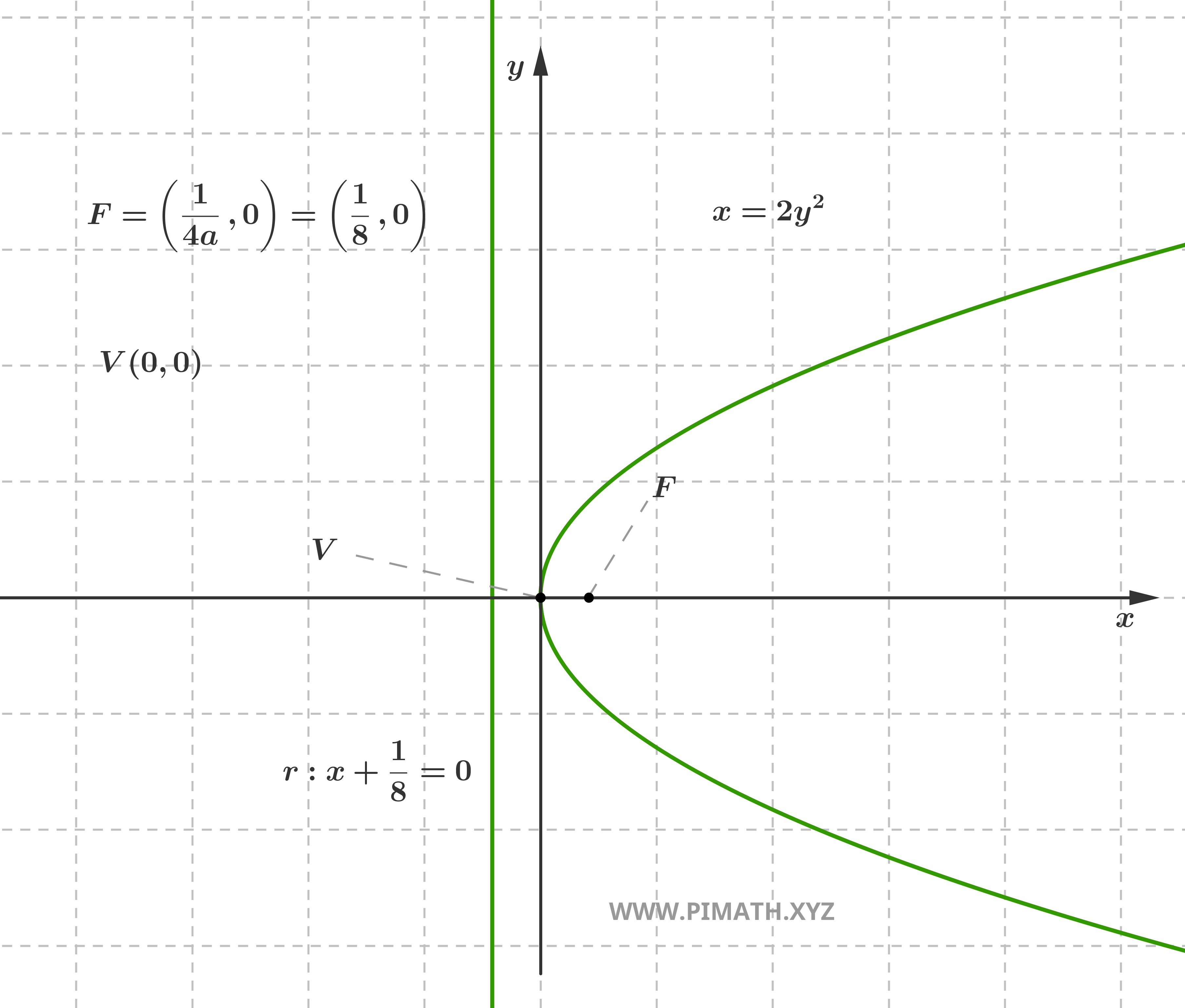
Para una parábola con eje de simetría horizontal, paralelo al eje de las abscisas, la ecuación canónica se convierte en \( x = ay^2 \) (si tomamos el foco en \( (p, 0)\)), o, equivalentemente, \( y^2 = 4px \). También en este caso, \( a = \displaystyle \frac{1}{4p} \) es el coeficiente director y \( p \) representa el parámetro focal.
Elementos característicos: el Vértice: \( V(0, 0) \), el Foco: \( F\left(\displaystyle \frac{1}{4a}, 0\right) \), la Directriz: \( x = -\displaystyle \frac{1}{4a} \) el Eje de simetría: \( y = 0 \) (eje \( x \)), y la Concavidad: hacia la derecha si \( a > 0 \), hacia la izquierda si \( a < 0 \).
Ejemplo: Consideremos la parábola \( x = \displaystyle 2y^2 \). Aquí \( a = 2 \), por tanto \( p = \displaystyle \frac{1}{4a} = \frac{1}{8} \). El vértice es \( V(0, 0) \), el foco se encuentra en \( F\left(\displaystyle \frac{1}{8}, 0\right) \) y la directriz tiene ecuación \( x = -\displaystyle \frac{1}{8} \). Puesto que \( a > 0 \), la parábola presenta concavidad hacia la derecha.
Relación entre los Parámetros
Es fundamental comprender la relación que liga el coeficiente \( a \) al parámetro focal \( p \), expresada por la fórmula \( a = \displaystyle \frac{1}{4p} \), que equivale a \( p = \displaystyle \frac{1}{4a} \). Esta relación nos permite convertir fácilmente de una forma a la otra de la ecuación canónica y determinar inmediatamente las características geométricas de la parábola una vez conocido uno de los dos parámetros.
Independientemente de la orientación del eje de simetría, cada punto \( P(x, y) \) perteneciente a la parábola respeta siempre la propiedad característica que define geométricamente esta cónica: la distancia del punto al foco es siempre igual a la distancia del punto a la directriz.
Parábola Trasladada en el Plano
Una parábola trasladada se obtiene operando una transformación del plano cartesiano (traslación). Este tipo de transformación geométrica mantiene inalterada la forma de la parábola, modificando únicamente su posición, y representa una de las herramientas más importantes para describir parábolas con vértice en puntos arbitrarios del plano.
Transformación de Traslación
La traslación es una transformación geométrica que desplaza cada punto del plano de un vector constante \( \vec{v} = (h, k) \). Si aplicamos una traslación de vector \( (h, k) \) a la parábola canónica \( y = ax^2 \), obtenemos una nueva parábola cuyo vértice se desplaza del origen al punto \( V(h, k) \).
Ecuación de la Parábola Trasladada con Eje Vertical
Partiendo de la parábola canónica \( y = ax^2 \) con vértice en el origen, una traslación de vector \( (h, k) \) produce la parábola trasladada de ecuación:
\[ y = a(x - h)^2 + k \]
Esta es la forma del vértice de la ecuación parabólica. El parámetro \( a \) mantiene su significado originario y determina la apertura y orientación de la parábola, mientras que \( h \) y \( k \) representan respectivamente la traslación horizontal y vertical del vértice.
Desarrollando la expresión \( (x - h)^2 = x^2 - 2hx + h^2 \), obtenemos la forma desarrollada:
\[ y = ax^2 - 2ahx + ah^2 + k \]
Poniendo \( b = -2ah \) y \( c = ah^2 + k \), encontramos la forma general \( y = ax^2 + bx + c \). De esta relación podemos deducir que \( h = -\displaystyle \frac{b}{2a} \) y \( k = c - ah^2 = c - \displaystyle \frac{b^2}{4a} \).
Elementos Geométricos de la Parábola Trasladada
Para una parábola trasladada \( y = a(x - h)^2 + k \), todos los elementos geométricos característicos sufren la misma traslación aplicada a la parábola canónica: el Vértice: \( V(h, k) \), el Eje de simetría: \( x = h \), el Foco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \) y la Directriz: \( y = k - \displaystyle \frac{1}{4a} \).
La distancia entre foco y directriz permanece invariada e igual a \( 2p = \displaystyle \frac{1}{2|a|} \), así como todas las propiedades métricas de la parábola.
Ejemplo de Parábola Trasladada
Consideremos la parábola \( y = 2(x - 3)^2 - 5 \). Esta es una parábola obtenida trasladando la parábola canónica \( y = 2x^2 \) de \( 3 \) unidades hacia la derecha y \( 5 \) unidades hacia abajo.
El vértice se encuentra en el punto \( V(3, -5) \), el eje de simetría tiene ecuación \( x = 3 \). El parámetro focal es \( p = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \).
Vértice, Foco, Directriz y Ejes de Simetría
Los elementos geométricos característicos de una parábola son el vértice, el foco y la directriz. Estos tres elementos están conectados entre sí y determinan completamente la forma y posición de la parábola en el plano cartesiano.
El Vértice de la Parábola
Definición. El vértice es el punto de la parábola que realiza el extremo absoluto (máximo o mínimo, depende del signo de \( a \)) de la función cuadrática \( f(x) = ax^2 + bx + c \).
Las coordenadas del vértice son:
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
donde \( \Delta = b^2 - 4ac \) es el discriminante.
Demostración. Transformamos la ecuación \( y = ax^2 + bx + c \) en forma canónica mediante completado del cuadrado:
\[ y = a\left(x^2 + \frac{b}{a}x\right) + c \]
\[ y = a\left(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2\right) + c \]
\[ y = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a} \]
De la forma canónica \( y = a(x - h)^2 + k \) se lee el vértice \( V(h, k) \), por tanto
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
Propiedades del vértice:
- Se encuentra sobre el eje de simetría \( x = -\displaystyle \frac{b}{2a} \)
- Es punto de mínimo si \( a > 0 \), de máximo si \( a < 0 \)
- Es el punto de la parábola más cercano a la directriz
El Foco de la Parábola
Definición. El foco es el punto fijo tal que cada punto de la parábola es equidistante del foco y de la directriz.
Coordenadas del foco:
\[ F\left(-\frac{b}{2a}, -\frac{\Delta}{4a} + \frac{1}{4a}\right) \]
Demostración. En la forma canónica trasladada \( Y = aX^2 \) (con \( X = x + \displaystyle \frac{b}{2a} \), \( Y = y + \displaystyle \frac{\Delta}{4a} \)), el foco se encuentra en \( \left(0, \displaystyle \frac{1}{4a}\right) \).
Para verificarlo, consideremos un punto \( P(X_0, aX_0^2) \) sobre la parábola. La distancia del foco candidato \( F\left(0, \displaystyle \frac{1}{4a}\right) \) es:
\[ d(P,F) = \sqrt{X_0^2 + \left(aX_0^2 - \frac{1}{4a}\right)^2} \]
La distancia de la directriz candidata \( Y = -\displaystyle \frac{1}{4a} \) es:
\[ d(P,d) = \left|aX_0^2 + \frac{1}{4a}\right| \]
Para \( a > 0 \), elevando al cuadrado y simplificando, se verifica que \( d(P,F) = d(P,d) \) para cada punto \( P \) de la parábola.
Volviendo al sistema original, obtenemos las coordenadas indicadas.
Parámetro focal: La distancia del vértice al foco es \( p = \displaystyle \frac{1}{4|a|} \).
La Directriz de la Parábola
Definición. La directriz es la recta fija tal que cada punto de la parábola es equidistante de la directriz y del foco.
Ecuación de la directriz:
\[ y = -\frac{\Delta}{4a} - \frac{1}{4a} \]
Demostración. De la verificación de la equidistancia para la forma canónica, la directriz tiene ecuación \( Y = -\displaystyle \frac{1}{4a} \) en el sistema trasladado. Volviendo al sistema original: \( y = Y - \displaystyle \frac{\Delta}{4a} = -\displaystyle \frac{1}{4a} - \displaystyle \frac{\Delta}{4a} \).
Propiedades de la directriz:
- Es perpendicular al eje de simetría
- Se encuentra a distancia \( p = \displaystyle \frac{1}{4|a|} \) del vértice, opuesta al foco
- La distancia foco-directriz es \( 2p = \displaystyle \frac{1}{2|a|} \)
El Eje de Simetría
El eje de simetría es la recta que pasa por el vértice y el foco, respecto a la cual la parábola es perfectamente simétrica. Para una parábola con eje vertical de ecuación \( y = ax^2 + bx + c \), el eje de simetría tiene ecuación \( x = -\displaystyle \frac{b}{2a} \).
Cada punto de la parábola tiene un punto simétrico respecto al eje de simetría. Si \( P(x_0, y_0) \) pertenece a la parábola, entonces también el punto \( P'(2x_V - x_0, y_0) \) pertenece a la parábola, donde \( x_V \) es la abscisa del vértice.
Relaciones entre los Elementos
Sistema coordinado: Los tres elementos forman un sistema con relaciones precisas:
- Vértice y foco yacen sobre el eje de simetría \( x = -\displaystyle \frac{b}{2a} \)
- La directriz es perpendicular al eje de simetría
- El vértice es equidistante del foco y de la directriz (distancia = parámetro focal \( p \))
- Si \( a > 0 \): foco arriba del vértice, directriz abajo
- Si \( a < 0 \): foco abajo del vértice, directriz arriba
Ejemplo Completo
Consideremos la parábola de ecuación \( y = 2x^2 - 8x + 3 \). Determinemos todos los elementos característicos.
En primer lugar, identificamos los coeficientes: \( a = 2 \), \( b = -8 \), \( c = 3 \). El discriminante es \( \Delta = b^2 - 4ac = 64 - 24 = 40 \).
El vértice tiene coordenadas \( V\left(-\displaystyle \frac{(-8)}{2 \cdot 2}, -\displaystyle \frac{40}{4 \cdot 2}\right) = V(2, -5) \).
El eje de simetría tiene ecuación \( x = 2 \).
Puesto que \( a = 2 \), el parámetro focal es \( p = \displaystyle \frac{1}{4|a|} = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \). Puesto que \( a > 0 \), la parábola tiene concavidad hacia arriba, por tanto el foco se encuentra arriba del vértice: \( F\left(2, -5 + \displaystyle \frac{1}{8}\right) = F\left(2, -\displaystyle \frac{39}{8}\right) \).
La directriz se encuentra debajo del vértice a distancia \( p \): \( y = -5 - \displaystyle \frac{1}{8} = -\displaystyle \frac{41}{8} \).
Formas Particulares
Forma canónica \( y = ax^2 \):
- Vértice: \( V(0, 0) \)
- Foco: \( F\left(0, \displaystyle \frac{1}{4a}\right) \)
- Directriz: \( y = -\displaystyle \frac{1}{4a} \)
Forma trasladada \( y = a(x - h)^2 + k \):
- Vértice: \( V(h, k) \)
- Foco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \)
- Directriz: \( y = k - \displaystyle \frac{1}{4a} \)
Ecuación de la Parábola Conocidos el Vértice y un Punto
Cuando son conocidos el vértice de la parábola y otro punto que pertenece a la curva, es posible determinar unívocamente la ecuación de la parábola. Este método es particularmente útil en las aplicaciones prácticas donde se conocen el punto de mínimo o máximo de una función cuadrática y un valor específico asumido por la función.
Forma General con Vértice Asignado
Dada una parábola con vértice \( V(h, k) \), la ecuación más conveniente a utilizar es la forma del vértice, que para una parábola con eje vertical se escribe como \( y = a(x - h)^2 + k \), donde \( a \) es el parámetro a determinar que controla la apertura y orientación de la parábola.
Procedimiento para Parábolas con Eje Vertical
Sea \( V(h, k) \) el vértice de la parábola y sea \( P(x_0, y_0) \) un punto perteneciente a la parábola con \( x_0 \neq h \). Sustituyendo las coordenadas del punto \( P \) en la ecuación \( y = a(x - h)^2 + k \), obtenemos:
\[ y_0 = a(x_0 - h)^2 + k \]
De esta ecuación podemos obtener directamente el valor del parámetro \( a \):
\[ a = \frac{y_0 - k}{(x_0 - h)^2} \]
Una vez determinado \( a \), la ecuación completa de la parábola se convierte en \( y = \displaystyle \frac{y_0 - k}{(x_0 - h)^2}(x - h)^2 + k \).
Ejemplo Numérico - Eje Vertical
Determinemos la ecuación de la parábola con vértice \( V(3, -2) \) y que pasa por el punto \( P(5, 6) \).
Utilizamos la forma del vértice \( y = a(x - 3)^2 - 2 \) y sustituimos las coordenadas del punto \( P(5, 6) \):
\[ 6 = a(5 - 3)^2 - 2 \]
\[ 6 = a \cdot 4 - 2 \]
\[ 8 = 4a \]
\[ a = 2 \]
La ecuación de la parábola es por tanto \( y = 2(x - 3)^2 - 2 \). Desarrollando esta expresión obtenemos \( y = 2(x^2 - 6x + 9) - 2 = 2x^2 - 12x + 18 - 2 = 2x^2 - 12x + 16 \).
Para verificar la corrección, controlamos que el vértice sea efectivamente \( V(3, -2) \). La abscisa del vértice es \( x_V = -\displaystyle \frac{b}{2a} = -\displaystyle \frac{-12}{2 \cdot 2} = 3 \) y la ordenada es \( y_V = 2 \cdot 3^2 - 12 \cdot 3 + 16 = 18 - 36 + 16 = -2 \).
Procedimiento para Parábolas con Eje Horizontal
Para parábolas con eje horizontal, la ecuación en forma del vértice se convierte en \( x = a(y - k)^2 + h \), donde \( V(h, k) \) es el vértice. Dado un punto \( P(x_0, y_0) \) perteneciente a la parábola con \( y_0 \neq k \), el parámetro \( a \) se determina con:
\[ a = \frac{x_0 - h}{(y_0 - k)^2} \]
Relación con el Parámetro Focal
Una vez determinado el coeficiente \( a \), es posible calcular todos los demás elementos característicos de la parábola. El parámetro focal es \( p = \displaystyle \frac{1}{4|a|} \), la distancia del vértice al foco. El foco se encuentra en el punto \( F(h, k + p) \) para parábolas con eje vertical y \( a > 0 \), mientras se encuentra en \( F(h, k - p) \) si \( a < 0 \).
Ejercicios Resueltos sobre la Parábola
Ejercicio 1. Dada la parábola de ecuación \( y = 3x^2 - 12x + 7 \), determinar vértice, foco, directriz y parámetro focal.
Solución. De la forma general \( y = ax^2 + bx + c \) identificamos los coeficientes \( a = 3 \), \( b = -12 \), \( c = 7 \).
El vértice está dado por la fórmula \[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \] donde \( \Delta = b^2 - 4ac = (-12)^2 - 4(3)(7) = 144 - 84 = 60 \). Sustituyendo:
\[ V\left(-\frac{-12}{2 \cdot 3}, -\frac{60}{4 \cdot 3}\right) = V\left(2, -5\right) \]
El parámetro focal es \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 3} = \frac{1}{12} \]
Puesto que \( a = 3 > 0 \), la parábola tiene concavidad hacia arriba y el foco se encuentra arriba del vértice:
\[ F\left(2, -5 + \frac{1}{12}\right) = F\left(2, -\frac{59}{12}\right) \]
La directriz está posicionada debajo del vértice a la misma distancia del foco:
\[ y = -5 - \frac{1}{12} = -\frac{61}{12} \]
Ejercicio 2. Determinar la ecuación de la parábola con eje vertical que tiene vértice \( V(-1, 4) \) y pasa por el punto \( P(2, -5) \).
Solución. Utilizamos la forma del vértice \( y = a(x - h)^2 + k \) donde \( V(h, k) = (-1, 4) \):
\[ y = a(x - (-1))^2 + 4 = a(x + 1)^2 + 4 \]
Para determinar el parámetro \( a \), sustituimos las coordenadas del punto \( P(2, -5) \):
\[ -5 = a(2 + 1)^2 + 4 \]
\[ -5 = 9a + 4 \]
\[ a = \frac{-9}{9} = -1 \]
La ecuación de la parábola es por tanto \( y = -(x + 1)^2 + 4 \).
Desarrollando la expresión obtenemos la forma estándar:
\[ y = -(x^2 + 2x + 1) + 4 = -x^2 - 2x + 3 \]
Ejercicio 3. Dada la parábola con eje horizontal \( x = 2y^2 - 8y + 6 \), determinar vértice, foco y directriz.
Solución. Para identificar el vértice, completamos el cuadrado respecto a la variable \( y \):
\begin{align} x &= 2(y^2 - 4y) + 6 \\ &= 2(y^2 - 4y + 4 - 4) + 6 \\ &= 2(y - 2)^2 - 8 + 6 \\ &= 2(y - 2)^2 - 2 \end{align}
De la forma \( x = a(y - k)^2 + h \) leemos directamente el vértice \( V(h, k) = V(-2, 2) \).
El parámetro focal es \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 2} = \frac{1}{8} \]
Puesto que \( a = 2 > 0 \), la parábola se abre hacia la derecha y el foco se encuentra a la derecha del vértice:
\[ F\left(-2 + \frac{1}{8}, 2\right) = F\left(-\frac{15}{8}, 2\right) \]
La directriz es la recta vertical posicionada a la izquierda del vértice:
\[ x = -2 - \frac{1}{8} = -\frac{17}{8} \]
Ejercicio 4. Dada la parábola \( y = -2x^2 + 8x - 5 \), determinar la ecuación de la parábola simétrica respecto al eje de las abscisas. Calcular además los puntos de intersección entre las dos parábolas.
Solución. La parábola simétrica respecto al eje de las abscisas se obtiene cambiando el signo de la variable \( y \). De la ecuación original \( y = -2x^2 + 8x - 5 \), la parábola simétrica tiene ecuación:
\[ y = 2x^2 - 8x + 5 \]
Para encontrar los puntos de intersección, resolvemos el sistema formado por las dos parábolas:
\[ \begin{cases} y = -2x^2 + 8x - 5 \\ y = 2x^2 - 8x + 5 \end{cases} \]
Igualando las dos expresiones:
\[ -2x^2 + 8x - 5 = 2x^2 - 8x + 5 \]
\[ -4x^2 + 16x - 10 = 0 \]
\[ -2(2x^2 - 8x + 5) = 0 \]
\[ 2x^2 - 8x + 5 = 0 \]
Aplicando la fórmula cuadrática:
\[ x = \frac{8 \pm \sqrt{64 - 40}}{4} = \frac{8 \pm \sqrt{24}}{4} = \frac{8 \pm 2\sqrt{6}}{4} = \frac{4 \pm \sqrt{6}}{2} \]
Las ordenadas correspondientes se calculan sustituyendo en una de las dos ecuaciones:
Para \( x_1 = \displaystyle \frac{4 + \sqrt{6}}{2} \) : \( y_1 = 2\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Para \( x_2 = \displaystyle \frac{4 - \sqrt{6}}{2} \) : \( y_2 = 2\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Los puntos de intersección son:
\[ A\left(\frac{4 + \sqrt{6}}{2}, -\frac{1}{2}\right) \quad \text{y} \quad B\left(\frac{4 - \sqrt{6}}{2}, -\frac{1}{2}\right) \]
Estando ambos puntos a la misma ordenada, la distancia entre ellos es simplemente:
\[ d(A,B) = \left|\frac{4 + \sqrt{6}}{2} - \frac{4 - \sqrt{6}}{2}\right| = \left|\frac{2\sqrt{6}}{2}\right| = \sqrt{6} \]
Ejercicio 5. Determinar la ecuación de la parábola con eje vertical que tiene foco \( F(1, 5) \) y directriz \( y = 3 \). Verificar si el punto \( P(3, 6) \) pertenece a la parábola.
Solución. El vértice de la parábola es el punto equidistante del foco y de la directriz, situado sobre la recta perpendicular a la directriz y que pasa por el foco. Puesto que la directriz es horizontal, el vértice tiene la misma abscisa del foco y ordenada igual a la media aritmética:
\[ V\left(1, \frac{5 + 3}{2}\right) = V(1, 4) \]
El parámetro focal es la distancia del vértice al foco:
\[ p = |5 - 4| = 1 \]
El coeficiente de la parábola es por tanto:
\[ a = \frac{1}{4p} = \frac{1}{4 \cdot 1} = \frac{1}{4} \]
La ecuación de la parábola en la forma del vértice es:
\[ y = \frac{1}{4}(x - 1)^2 + 4 \]
Para verificar si \( P(3, 6) \) pertenece a la parábola, sustituimos sus coordenadas:
\[ y = \frac{1}{4}(3 - 1)^2 + 4 = \frac{1}{4} \cdot 4 + 4 = 1 + 4 = 5 \neq 6 \]
Confirmamos el resultado utilizando la definición geométrica de la parábola. La distancia de P del foco es:
\[ d(P,F) = \sqrt{(3-1)^2 + (6-5)^2} = \sqrt{4 + 1} = \sqrt{5} \]
La distancia de P de la directriz es:
\[ d(P, \text{directriz}) = |6 - 3| = 3 \]
Puesto que \( \sqrt{5} \neq 3 \), el punto \( P(3, 6) \) no pertenece a la parábola.

