Sean \( P_1(x_1,y_1) \) y \( P_2(x_2,y_2) \) dos puntos distintos en el plano cartesiano. La recta que pasa por estos dos puntos tiene la ecuación:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
que, multiplicando ambos miembros por \( y_2 - y_1 \), se convierte en:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1). \]
- Semejanza de triángulos
- Interpretación geométrica
- Transformación en la ecuación explícita
- Forma explícita de la recta
- Pendiente de la recta
- Interpretación de la pendiente
- Forma implícita de la recta
- Ecuación paramétrica de la recta
- Recta perpendicular
- Ejercicios
Para demostrar la ecuación de la recta que pasa por dos puntos, consideremos los puntos distintos \( P_1(x_1,y_1) \) y \( P_2(x_2,y_2) \) en el plano cartesiano. Queremos demostrar que la ecuación:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
se satisface para cada punto \( P(x,y) \) que pertenece a la recta.
Semejanza de triángulos
Consideremos los triángulos en la figura. Son semejantes por el criterio del ángulo en común (ángulo entre la recta y el eje de abscisas) y por la proporcionalidad de los lados correspondientes:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
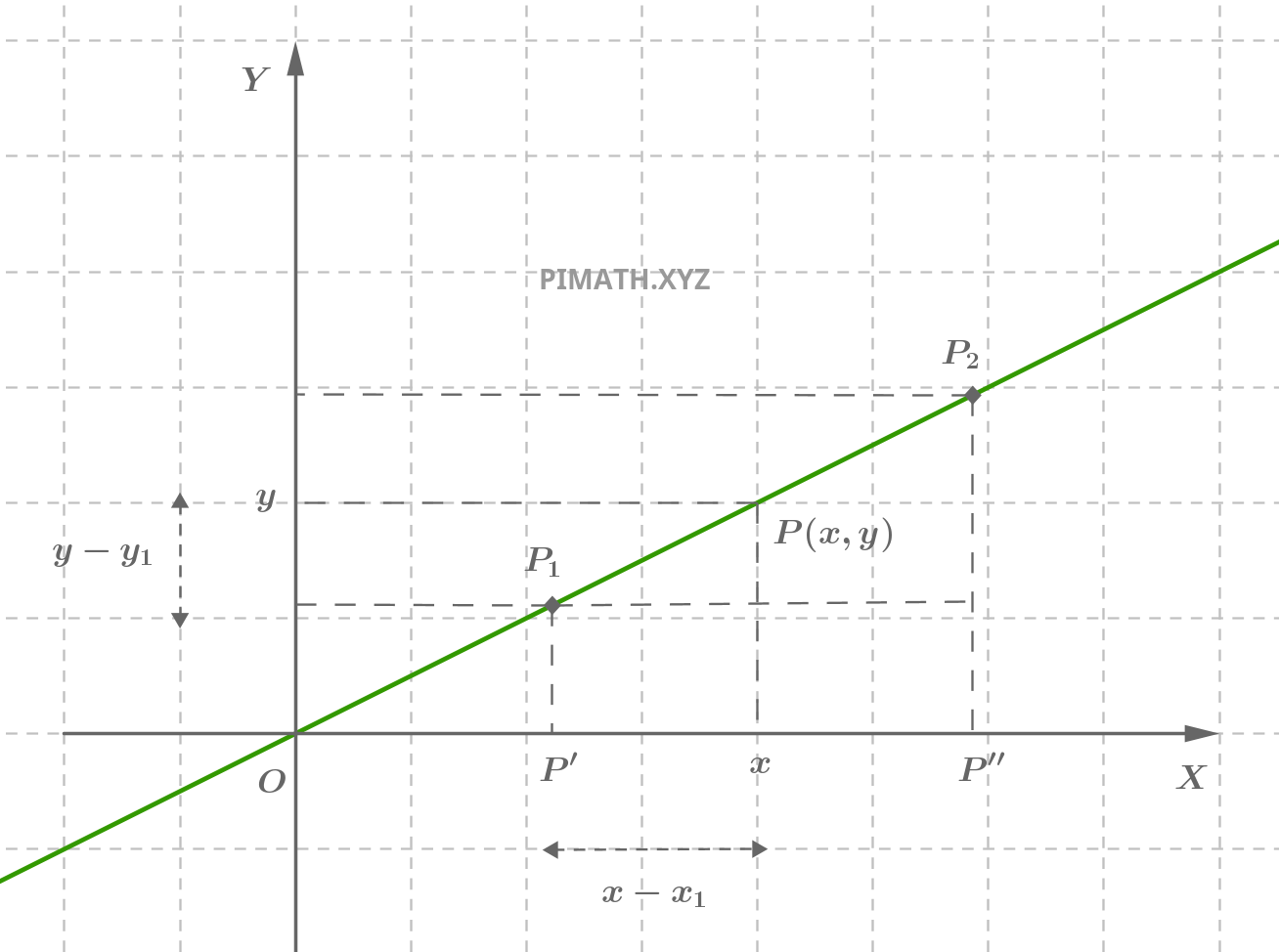
Esta relación se sigue directamente de la propiedad de la semejanza de los triángulos, garantizando que la razón entre las diferencias de ordenadas y abscisas permanece constante a lo largo de la recta.
Interpretación geométrica
La fracción \( \displaystyle \frac{y - y_1}{y_2 - y_1} \) representa la relación entre la altura del punto genérico \( P \) respecto a \( P_1 \) y la altura total entre \( P_1 \) y \( P_2 \). De manera análoga, \( \displaystyle \frac{x - x_1}{x_2 - x_1} \) mide la relación análoga para las abscisas. La igualdad entre estas dos razones indica que el punto \( P \) está alineado con \( P_1 \) y \( P_2 \), es decir, pertenece a la recta que pasa por estos dos puntos.
Transformación en la ecuación explícita
Multiplicando ambos miembros por \( y_2 - y_1 \), obtenemos:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1), \]
que es la ecuación de la recta en forma explícita \( y = mx + q \), con pendiente \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \).
Esta forma de la ecuación es fundamental para describir la relación lineal entre \( x \) y \( y \) para todos los puntos de la recta que pasa por \( P_1 \) y \( P_2 \).
Forma explícita de la recta
La ecuación de la recta que pasa por dos puntos distintos \( P_1(x_1, y_1) \) y \( P_2(x_2, y_2) \) puede expresarse en forma explícita de la siguiente manera:
\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) \]
Esta ecuación relaciona la variable \( y \) con la variable \( x \) a lo largo de la recta. En otras palabras, para cada valor de \( x \) elegido, la ecuación nos permite determinar el valor correspondiente de \( y \), que es la coordenada del punto sobre la recta.
Pendiente de la recta
En el contexto de esta ecuación, el término:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
representa la pendiente de la recta, es decir, el coeficiente angular. La pendiente es una medida de la inclinación de la recta con respecto al eje de abscisas (el eje \( x \)). Si la pendiente es positiva, la recta es creciente (sube de izquierda a derecha); si es negativa, la recta es decreciente (baja de izquierda a derecha).
En otras palabras, la pendiente describe la velocidad con la que la recta crece o decrece en relación con el eje horizontal \( x \). La pendiente es un parámetro crucial para determinar la orientación de la recta en el plano cartesiano.
Interpretación de la Pendiente
La pendiente \( m \) de una recta que pasa por dos puntos \( P_1(x_1, y_1) \) y \( P_2(x_2, y_2) \) está dada por la fórmula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
La pendiente mide la inclinación de la recta con respecto al eje de abscisas \( x \). Dependiendo del valor de la pendiente, podemos hacer las siguientes observaciones:
- Si \( m > 0 \), la recta es creciente, es decir, sube de izquierda a derecha. Esto significa que por cada incremento en \( x \), también \( y \) aumenta. La recta forma un ángulo agudo con el eje \( x \).
- Si \( m < 0 \), la recta es decreciente, es decir, baja de izquierda a derecha. En este caso, por cada incremento en \( x \), el valor de \( y \) disminuye. La recta forma un ángulo obtuso con el eje \( x \).
- Si \( x_2 = x_1 \), la pendiente es indefinida, lo que implica que la recta es vertical. En este caso, no hay un cambio horizontal (la diferencia entre las abscisas \( x_2 - x_1 \) es cero), por lo que no se puede definir una pendiente numérica. La recta es paralela al eje \( y \) y no tiene ninguna inclinación horizontal.
En general, la pendiente \( m \) nos proporciona información importante sobre el comportamiento de la recta. Si la recta es creciente, el valor de \( y \) aumenta a medida que \( x \) aumenta; si es decreciente, el valor de \( y \) disminuye a medida que \( x \) aumenta; si la recta es vertical, significa que \( y \) no depende de \( x \) y la recta no tiene ninguna inclinación horizontal.
Implicit Form of the Line
Starting from the explicit form of the equation of a line:
\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
we can multiply both sides by \( x_2 - x_1 \) to obtain a more general version and rewrite the equation as follows:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
Multiplying both sides of the equation by \( (x_2 - x_1) \), we obtain:
\[ (y - y_1)(x_2 - x_1) = (y_2 - y_1)(x - x_1) \]
Expanding the terms, we get:
\[ (x_2 - x_1) y - (x_2 - x_1) y_1 = (y_2 - y_1) x - (y_2 - y_1) x_1 \]
Now, to obtain an implicit form, we want to gather the terms so that the equation is in a linear form that does not explicitly solve for \( y \). Bringing the terms containing \( y \) and \( x \) to one side:
\[ (y_2 - y_1) x - (x_2 - x_1) y = (y_2 - y_1) x_1 - (x_2 - x_1) y_1 \]
Writing this equation in the standard implicit form:
\[ (y_2 - y_1) x - (x_2 - x_1) y + ((x_2 - x_1) y_1 - (y_2 - y_1) x_1) = 0 \]
This is the implicit form of the equation of a line. If we define the coefficients as \( a = y_2 - y_1 \), \( b = -(x_2 - x_1) \), and \( c = (x_2 - x_1) y_1 - (y_2 - y_1) x_1 \), the equation takes the general form:
\[ ax + by + c = 0. \]
Alternatively, if we introduce the slope \( m = \frac{y_2 - y_1}{x_2 - x_1} \) and rearrange the terms in the previous equation, we can write:
\[ m(x_2 - x_1)x - (x_2 - x_1)y + ((x_2 - x_1)y_1 - m(x_2 - x_1)x_1) = 0 \]
Simplifying and dividing by \( (x_2 - x_1) \), we obtain:
\[ mx - y + (y_1 - mx_1) = 0. \]
In this form, the coefficients are \( a = m \), \( b = -1 \), and \( c = y_1 - mx_1 \).
The implicit form \( ax + by + c = 0 \) is a more general representation of a line in the Cartesian plane. This format is particularly useful for geometric and algebraic applications, where the explicit value of \( y \) is not necessary or where one wants to work directly with the algebraic properties of the line.
Parametric Equation of the Line
The line passing through the points \( P_1(x_1, y_1) \) and \( P_2(x_2, y_2) \) can also be described in parametric form. In this representation, the coordinates \( x \) and \( y \) of a point on the line are expressed as functions of a real parameter \( t \), which varies along the line.
The parametric equation of the line is given by:
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Here, \( t \) is the parameter that can take any real value. As \( t \) varies, the point \( (x, y) \) moves along the line connecting the two points \( P_1 \) and \( P_2 \).
The parametric form thus represents a family of points on the line, where the parameter \( t \) uniquely defines each point. When \( t = 0 \), we obtain the point \( P_1(x_1, y_1) \); when \( t = 1 \), we obtain the point \( P_2(x_2, y_2) \). Values of \( t \) between 0 and 1 describe points on the line segment between \( P_1 \) and \( P_2 \), while values of \( t \) greater than 1 or less than 0 extend the line beyond these points.
The parametric formula is based on the concept of a direction vector, which is the vector connecting \( P_1 \) and \( P_2 \). Specifically, the difference \( (x_2 - x_1, y_2 - y_1) \) is the direction vector of the line, and the parameter \( t \) is the scaling factor that allows movement along the line.
In vector form, the parametric equation can be written as:
\[ \vec{r}(t) = \vec{P_1} + t \cdot (\vec{P_2} - \vec{P_1}) \]
where \( \vec{r}(t) \) represents the position of a generic point on the line at time \( t \), and \( \vec{P_1} \) and \( \vec{P_2} \) are the position vectors of the points \( P_1 \) and \( P_2 \), respectively.
The parametric form is particularly useful in various fields of analytic geometry, such as in the study of curves, computer graphics applications, or physics to describe the motion of an object along a straight path.
Recta Perpendicular
Cuando dos rectas son perpendiculares, su pendiente está relacionada por una ecuación precisa. Si una recta tiene pendiente \( m \), la pendiente de la recta perpendicular a ella está dada por:
\[ m_\perp = -\frac{1}{m}. \]
Esta fórmula expresa el hecho de que el producto de las pendientes de dos rectas perpendiculares es igual a \(-1\). La razón de esta relación se puede entender considerando que los ángulos formados por las dos rectas deben ser de 90° (un ángulo recto), por lo que la tangente del ángulo entre las rectas debe satisfacer esta condición.
Para encontrar la ecuación de la recta perpendicular que pasa por un punto \( (x_1, y_1) \), podemos usar la forma punto-pendiente. La pendiente de la recta perpendicular es \( -\displaystyle \frac{1}{m} \), por lo que la ecuación de la recta perpendicular será:
\[ y - y_1 = -\frac{1}{m} (x - x_1) \]
En esta ecuación, \( (x_1, y_1) \) es el punto por el cual pasa la recta perpendicular, mientras que \( m \) es la pendiente de la recta original. La fórmula describe una recta que tiene pendiente opuesta e inversa con respecto a la recta original.
Si la recta original está representada por la ecuación \( y = mx + q \), la recta perpendicular tendrá pendiente \( m_\perp = -\displaystyle \frac{1}{m} \) y estará escrita en la forma \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), donde \( (x_1, y_1) \) es el punto de intersección entre la recta original y la recta perpendicular.
Esta propiedad de las rectas perpendiculares es fundamental en muchos ámbitos de la geometría, la trigonometría y la física, especialmente al estudiar ángulos y trayectorias perpendiculares entre sí.
Ejercicios
Ejercicio 1: Determina la ecuación de la recta que pasa por \( A(1, 2) \) y \( B(3, 6) \).
Solución:
- Calculamos la pendiente de la recta: \[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- Utilizamos la ecuación punto-pendiente para determinar la ecuación de la recta que pasa por \( A(1, 2) \) y tiene pendiente \( m = 2 \): \[ y - 2 = 2(x - 1). \]
- Desarrollando la ecuación: \[ y - 2 = 2x - 2. \]
- Simplificando: \[ y = 2x - 2 + 2 = 2x. \]
Entonces, la ecuación de la recta que pasa por los puntos \( A(1, 2) \) y \( B(3, 6) \) es \[ y = 2x. \]
Verificación: Podemos verificar que ambos puntos satisfacen esta ecuación:
- Para \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
- Para \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]
Ejercicio 2: Escribe la ecuación paramétrica de la recta que pasa por \( A(1, 2) \) y \( B(3, 6) \).
Solución:
- Calculamos el vector director \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), que representa la dirección de la recta: \[ \boldsymbol{v} = (3 - 1, 6 - 2) = (2, 4). \]
- Las ecuaciones paramétricas de la recta son: \[ \begin{cases} x = 1 + 2t \\ y = 2 + 4t \end{cases} \quad \text{con} \quad t \in \mathbb{R}. \]

