La recta es un concepto primitivo de la geometría euclídea, es decir, no puede definirse en términos más elementales y se asume como un ente fundamental. Intuitivamente, se describe como un conjunto infinito de puntos alineados en una misma dirección, extendiéndose indefinidamente en ambos sentidos. En un sistema de coordenadas cartesianas, una recta puede representarse mediante una ecuación lineal y se caracteriza por un coeficiente angular que determina su inclinación respecto al eje de abscisas.
Índice
- Cómo determinar la ecuación de la recta que pasa por dos puntos
- Cómo obtener la ecuación explícita de una recta
- Cómo obtener la ecuación implícita de una recta
- Significado geométrico del coeficiente angular
- Cómo hallar la ecuación paramétrica de una recta
- Cómo determinar la recta perpendicular a una recta dada
- Ejercicios resueltos sobre la recta
Cómo determinar la ecuación de la recta que pasa por dos puntos
Supongamos que se conocen dos puntos distintos del plano cartesiano: \( P_1(x_1, y_1) \) y \( P_2(x_2, y_2) \).
La ecuación que satisface cualquier punto perteneciente a la recta que pasa por \( P_1 \) y \( P_2 \) viene dada por la siguiente expresión:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
Esta fórmula se fundamenta en la semejanza de los triángulos \( \triangle P_1P'P \) y \( \triangle P_1P'_2P_2 \) mostrados en la figura:
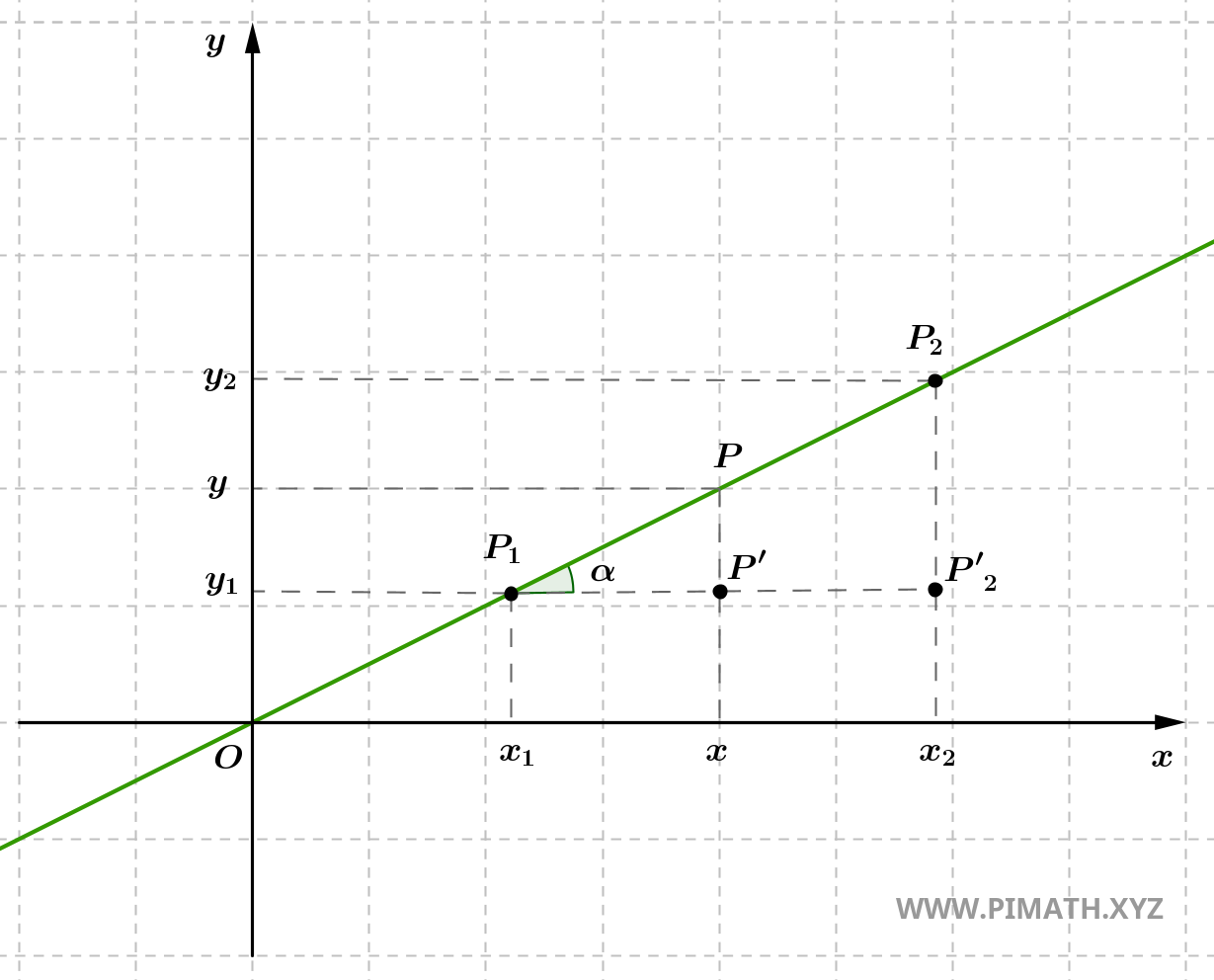
Dicha semejanza se justifica por el primer criterio de semejanza de triángulos, que establece que dos triángulos son semejantes si tienen dos ángulos respectivamente congruentes. En este caso, ambos triángulos comparten un ángulo recto y un ángulo agudo congruente, determinado por la inclinación de la recta con respecto al eje \( x \). De ello se deduce la proporcionalidad entre los lados correspondientes.
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
Resolviendo esta igualdad con respecto a \( y \), se obtiene la forma explícita de la ecuación de la recta:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \]
El ángulo agudo común a los dos triángulos, habitualmente denotado por \( \alpha \), representa el ángulo de inclinación de la recta con respecto al eje \( x \). Este ángulo tiene una importancia fundamental en la geometría de la recta, ya que su tangente proporciona la pendiente de la recta, es decir:
\[ m = \tan \alpha = \frac{y_2 - y_1}{x_2 - x_1}. \]
Esta relación permite interpretar la pendiente como una medida de la inclinación angular de la recta en el plano cartesiano.
Cómo obtener la ecuación explícita de una recta
La ecuación de una recta que pasa por dos puntos distintos \( P_1(x_1, y_1) \) y \( P_2(x_2, y_2) \) puede expresarse en forma explícita utilizando la denominada forma punto-pendiente:
\[ y = y_1 + m(x - x_1) \]
donde
\[ m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]
es el coeficiente angular de la recta. Esta expresión permite determinar el valor de \( y \) correspondiente a cualquier valor dado de \( x \), a partir de un punto conocido sobre la recta y su pendiente.
A partir de esta fórmula, se puede obtener la forma explícita canónica de la ecuación de la recta:
\[ y = mx + q \]
En esta ecuación:
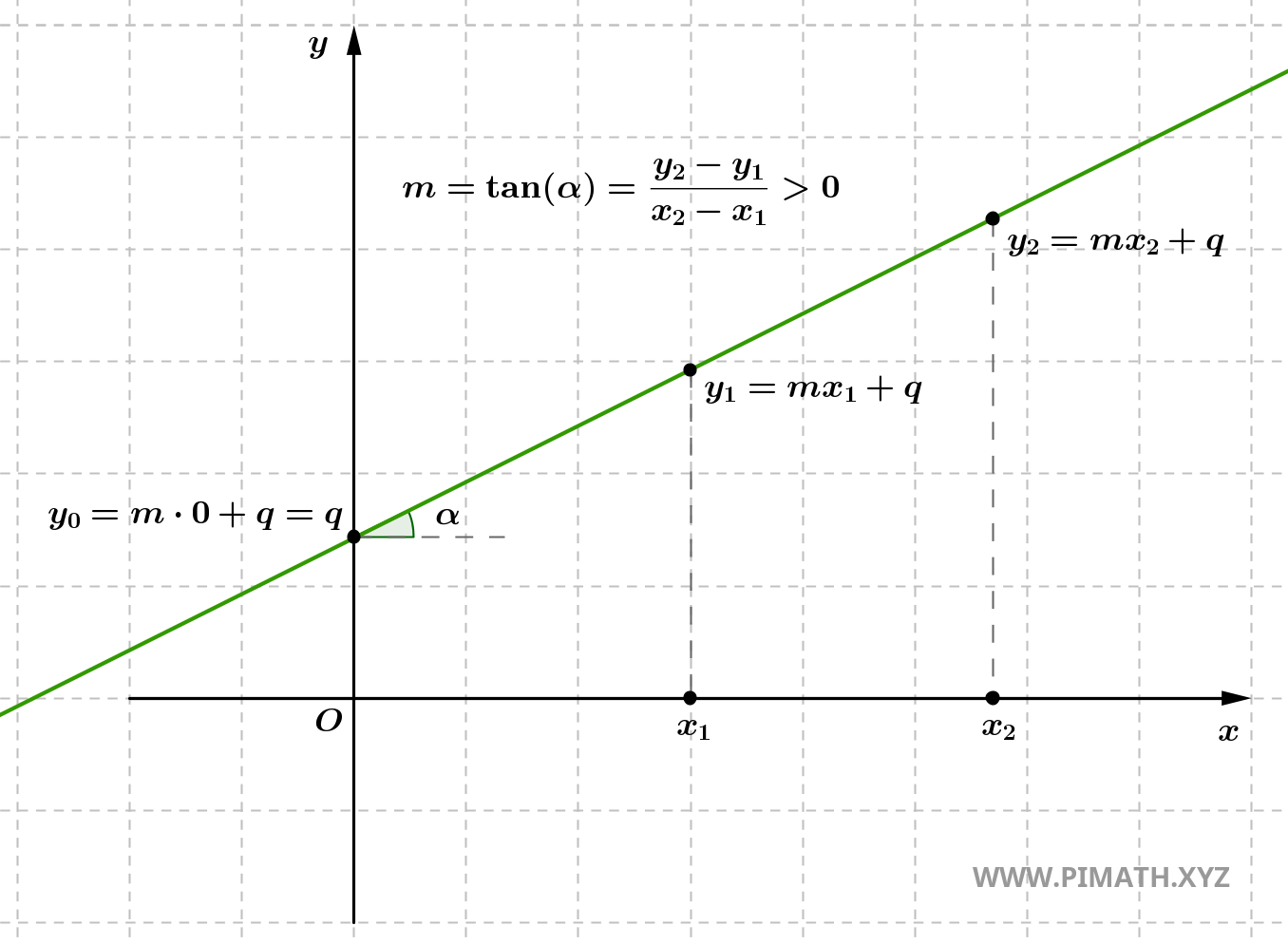
- \( m \) es el coeficiente angular, que representa la pendiente de la recta;
- \( q \) es la ordenada al origen, es decir, el valor de \( y \) cuando la recta corta al eje de ordenadas (es decir, cuando \( x = 0 \)).
Esta forma es especialmente útil porque pone de manifiesto tanto la dirección de la recta (a través de \( m \)) como su punto de intersección con el eje \( y \) (a través de \( q \)). Conociendo \( m \) y \( q \), es posible trazar la recta sin necesidad de conocer otros puntos.
Para pasar de la forma punto-pendiente a la forma canónica, basta con desarrollar los cálculos y aislar \( y \). Por ejemplo:
\[ y = y_1 + m(x - x_1) = mx + (y_1 - mx_1) \]
De donde se obtiene directamente:
\[ y = mx + q \quad \text{con} \quad q = y_1 - mx_1 \]
Cómo obtener la ecuación implícita de una recta
Partamos de la forma punto-pendiente de la ecuación de la recta que pasa por dos puntos \( (x_1, y_1) \) y \( (x_2, y_2) \):
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
Multiplicamos ambos miembros por \( x_2 - x_1 \neq 0 \):
\[ (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1) \]
Desarrollamos ambos lados:
\[ (x_2 - x_1)y - (x_2 - x_1)y_1 = (y_2 - y_1)x - (y_2 - y_1)x_1 \]
Reuniendo todos los términos en el primer miembro:
\[ (x_2 - x_1)y - (y_2 - y_1)x + \left( (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \right) = 0 \]
Esta es la forma implícita de la ecuación de la recta. Si definimos los coeficientes de la siguiente manera:
\[ \begin{cases} a = -(y_2 - y_1) \\ b = x_2 - x_1 \\ c = (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \end{cases} \]
entonces la ecuación adquiere la forma general:
\[ ax + by + c = 0 \]
Alternativamente, si introducimos la pendiente \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \), podemos partir de la forma explícita:
\[ y = m(x - x_1) + y_1 \]
Reuniendo todos los términos en el primer miembro obtenemos:
\[ y - m x + (m x_1 - y_1) = 0 \]
Así, la forma implícita de la recta con pendiente \( m \) es:
\[ a = -m, \quad b = 1, \quad c = m x_1 - y_1 \]
y la forma general:
\[ ax + by + c = 0 \]
La forma implícita resulta especialmente útil al estudiar propiedades geométricas de la recta o para verificar si un punto pertenece a la recta sin necesidad de despejar \( y \).
Significado geométrico del coeficiente angular
En el contexto de esta ecuación, el término:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
representa la pendiente de la recta, es decir, su coeficiente angular. La pendiente mide la inclinación de la recta con respecto al eje de abscisas (eje \( x \)). Si la pendiente es positiva, la recta es creciente (asciende de izquierda a derecha); si es negativa, la recta es decreciente (desciende de izquierda a derecha).
En otras palabras, la pendiente describe la rapidez con la que cambia el valor de \( y \) respecto a \( x \). Se trata de un parámetro fundamental para determinar la orientación de la recta en el plano cartesiano. Según el valor que tome la pendiente, podemos hacer las siguientes observaciones:
- Si \( m > 0 \), la recta es creciente, es decir, asciende de izquierda a derecha. Esto significa que, al aumentar \( x \), también aumenta \( y \). La recta forma un ángulo agudo con el eje \( x \).
- Si \( m < 0 \), la recta es decreciente, es decir, desciende de izquierda a derecha. En este caso, al aumentar \( x \), el valor de \( y \) disminuye. La recta forma un ángulo obtuso con el eje \( x \).
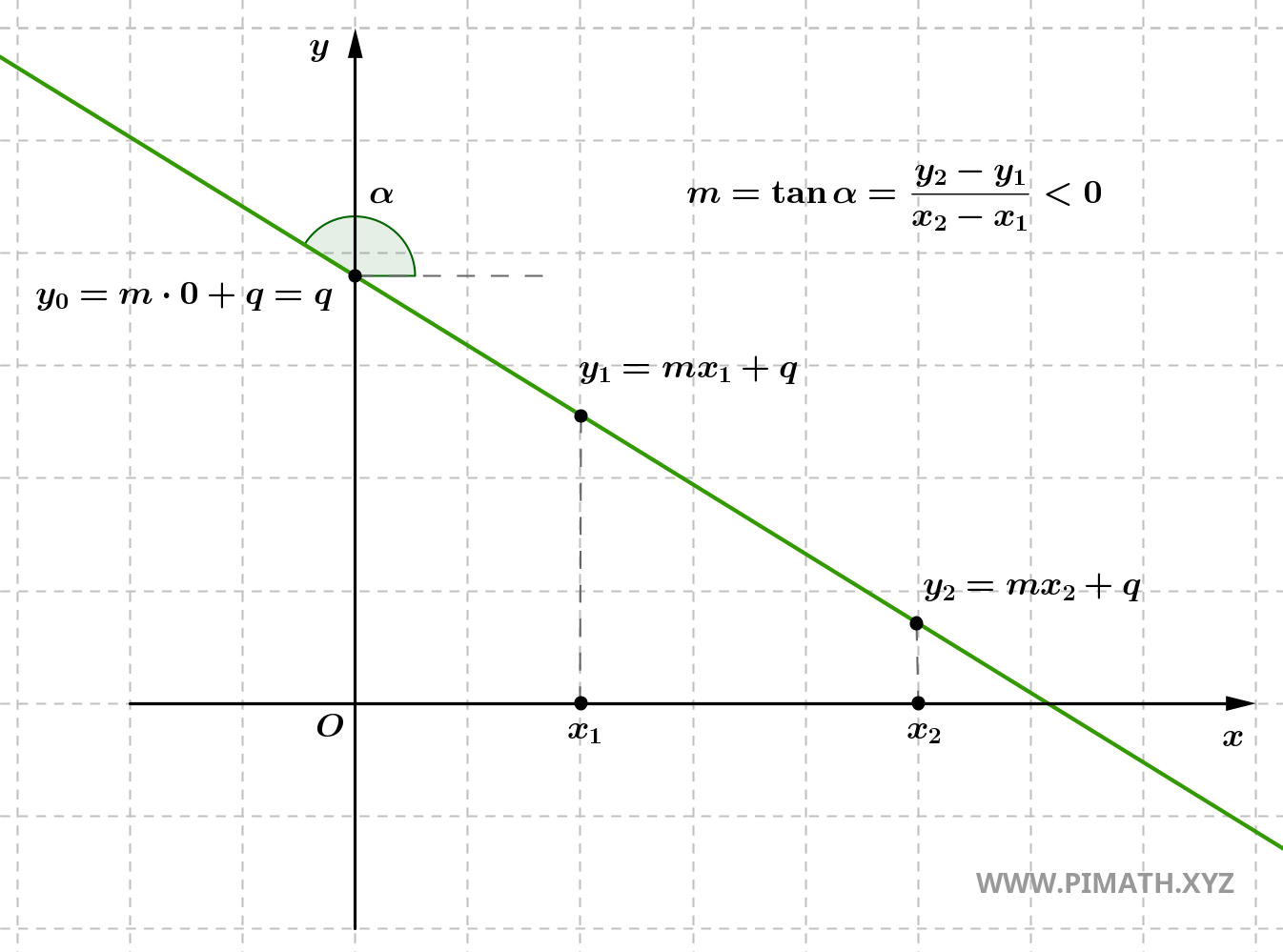
- Si \( y_2 = y_1 \), la pendiente es nula, lo cual indica que la recta es horizontal. En este caso, no hay variación vertical entre los puntos, es decir, \( y_2 - y_1 = 0 \). La recta es paralela al eje \( x \) y carece de inclinación.
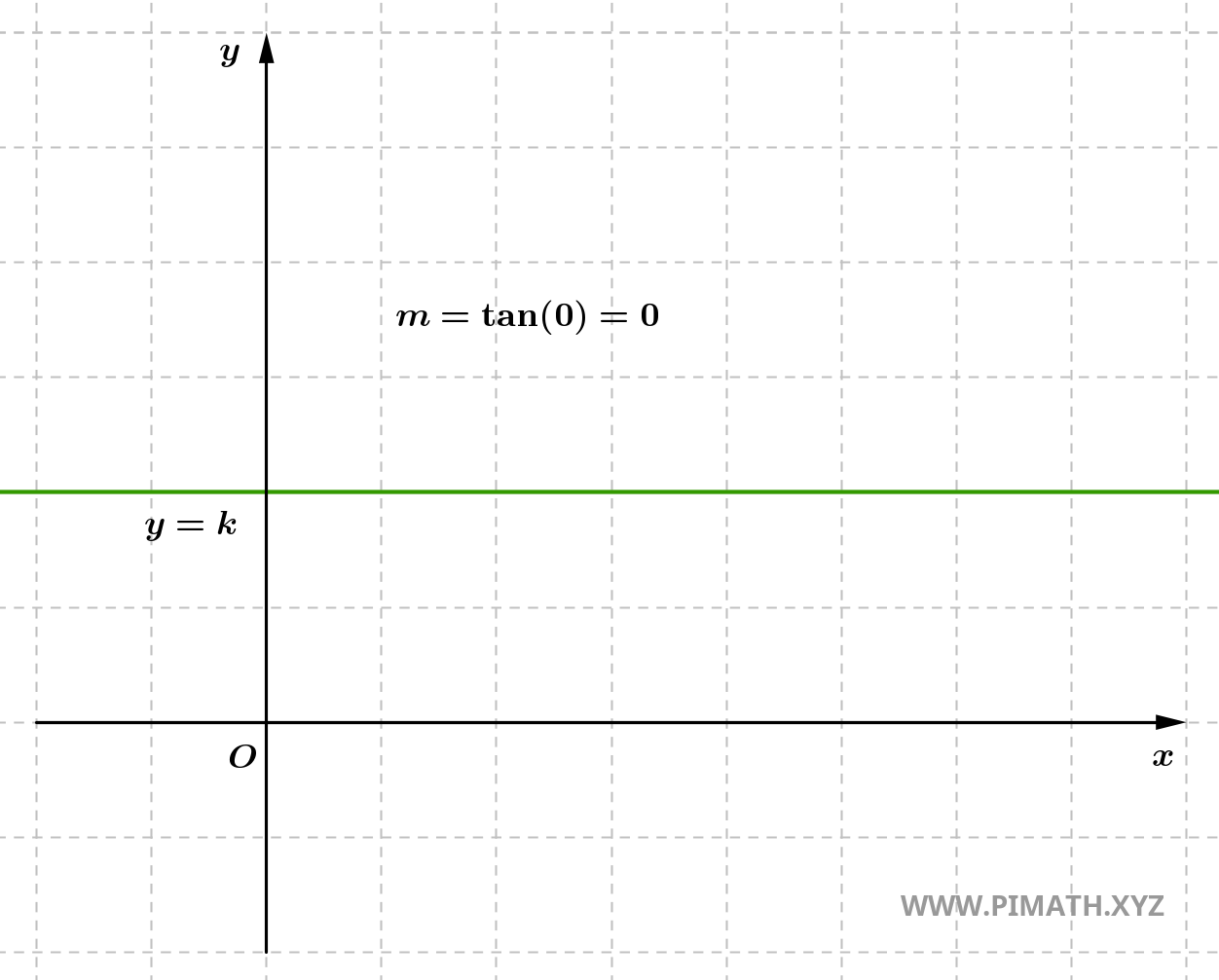
- Si \( x_2 = x_1 \), la pendiente es indefinida, lo que implica que la recta es vertical. En este caso, no hay cambio en la coordenada \( x \), es decir, \( x_2 - x_1 = 0 \), por lo que no es posible calcular numéricamente la pendiente. La recta es paralela al eje \( y \).
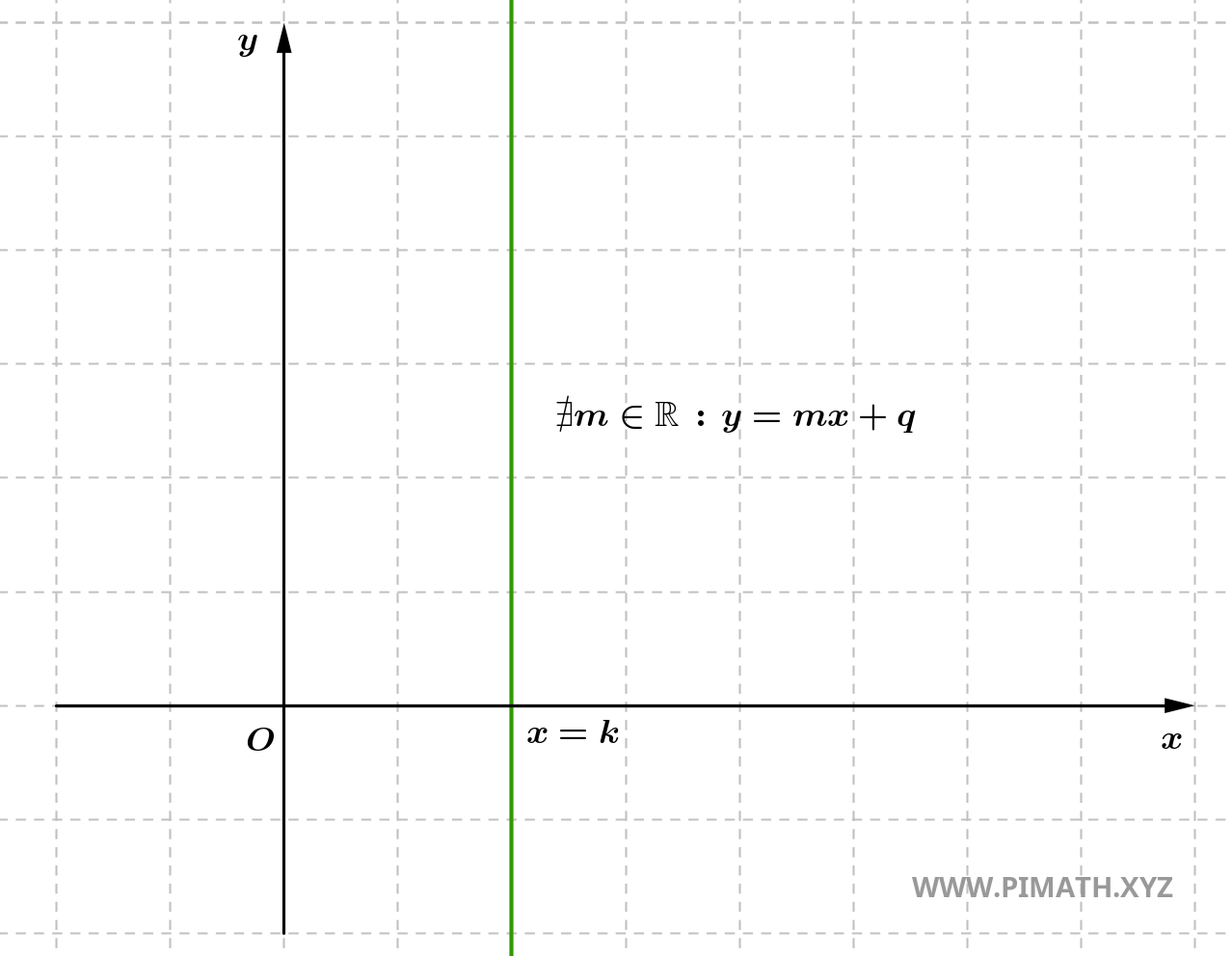
En general, el coeficiente angular \( m \) proporciona información clave sobre el comportamiento de la recta: si esta es creciente, decreciente, horizontal o vertical. Es un parámetro esencial en el estudio de funciones lineales y en el análisis geométrico del plano.
Cómo obtener la ecuación paramétrica de una recta
Una recta que pasa por los puntos \( P_1(x_1, y_1) \) y \( P_2(x_2, y_2) \) también puede describirse mediante una representación paramétrica. En esta formulación, las coordenadas \( x \) e \( y \) de un punto genérico sobre la recta se expresan en función de un parámetro real \( t \), que recorre todos los puntos de la recta.
La ecuación paramétrica de la recta se expresa como:
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Aquí, \( t \in \mathbb{R} \) es un parámetro libre que permite recorrer la totalidad de la recta. Cuando \( t = 0 \), se obtiene el punto \( P_1 \); cuando \( t = 1 \), se alcanza el punto \( P_2 \). Para \( 0 < t < 1 \), se recorren los puntos del segmento entre \( P_1 \) y \( P_2 \), mientras que para \( t < 0 \) o \( t > 1 \), se extiende la recta más allá de esos extremos.
Esta representación se fundamenta en el uso de un vector director de la recta, dado por la diferencia de coordenadas entre los dos puntos:
\[ \vec{v} = (x_2 - x_1,\ y_2 - y_1). \]
Así, el punto genérico sobre la recta se obtiene sumando al punto fijo \( P_1 \) un múltiplo del vector director. Esto proporciona una descripción dinámica de la recta, especialmente útil en el estudio de trayectorias, cinemática, geometría analítica y representación de líneas en el espacio.
Cómo determinar la recta perpendicular a una dada
Cuando dos rectas son perpendiculares, sus pendientes están relacionadas mediante una propiedad fundamental. Si una recta tiene pendiente \( m \), entonces la pendiente de una recta perpendicular a ella es:
\[ m_{\perp} = -\frac{1}{m}. \]
Esta relación expresa que el producto de las pendientes de dos rectas perpendiculares es igual a \( -1 \), es decir:
\[ m \cdot m_{\perp} = -1. \]
Esta propiedad puede derivarse del hecho de que dos rectas perpendiculares forman un ángulo recto de \( 90^\circ \), cuya tangente satisface la condición anterior.
Para determinar la ecuación de la recta perpendicular que pasa por un punto dado \( (x_1, y_1) \), se utiliza la forma punto-pendiente con la pendiente opuesta e inversa:
\[ y - y_1 = -\frac{1}{m}(x - x_1). \]
En esta ecuación, \( m \) representa la pendiente de la recta original, mientras que \( (x_1, y_1) \) es el punto por el cual debe pasar la recta perpendicular. Esta formulación da lugar a una nueva recta cuya inclinación es ortogonal a la recta inicial.
Si la recta original se encuentra en forma explícita como \( y = mx + q \), entonces la perpendicular correspondiente tendrá pendiente \( m_{\perp} = -\displaystyle \frac{1}{m} \), y su ecuación será:
\[ y - y_1 = -\frac{1}{m}(x - x_1), \]
donde \( (x_1, y_1) \) es el punto de paso. Esta fórmula permite construir rectas perpendiculares en múltiples contextos, como en la resolución de problemas de geometría euclidiana, en el análisis de trayectorias ortogonales o en aplicaciones físicas donde se requiere perpendicularidad entre vectores o direcciones.
Ejercicios Resueltos sobre la Recta
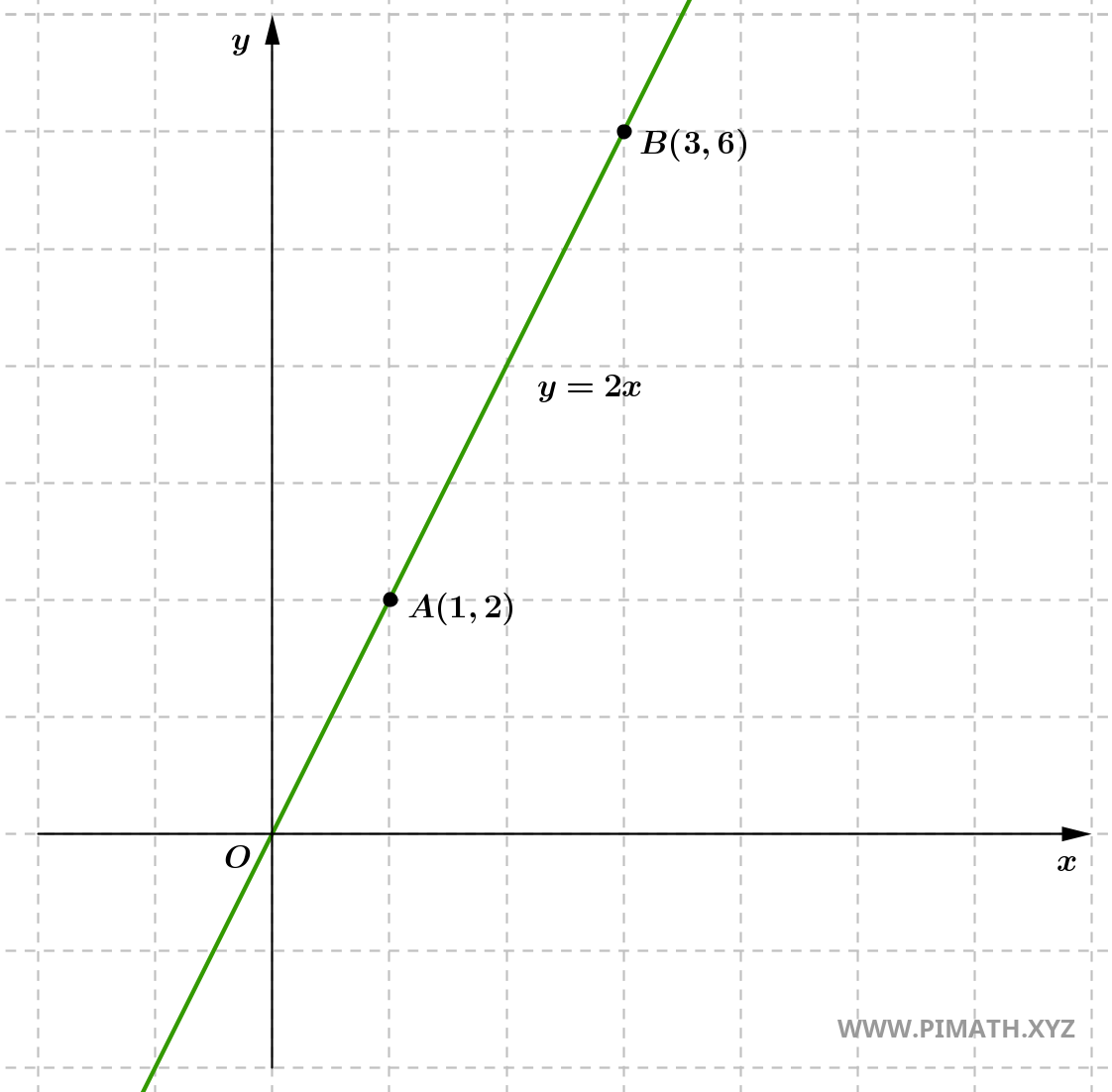
Ejercicio 1: Determina la ecuación explícita de la recta que pasa por los puntos \( A(1, 2) \) y \( B(3, 6) \).
Solución. Calculamos la pendiente:
\[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- Usamos la forma punto-pendiente: \[ y - 2 = 2(x - 1). \]
- Desarrollamos: \[ y - 2 = 2x - 2. \]
- Simplificamos: \[ y = 2x. \]
Por tanto, la ecuación es: \[ y = 2x. \]
Verificación:
- Para \( A(1, 2) \): \[ y = 2 \cdot 1 = 2 \]
- Para \( B(3, 6) \): \[ y = 2 \cdot 3 = 6 \]
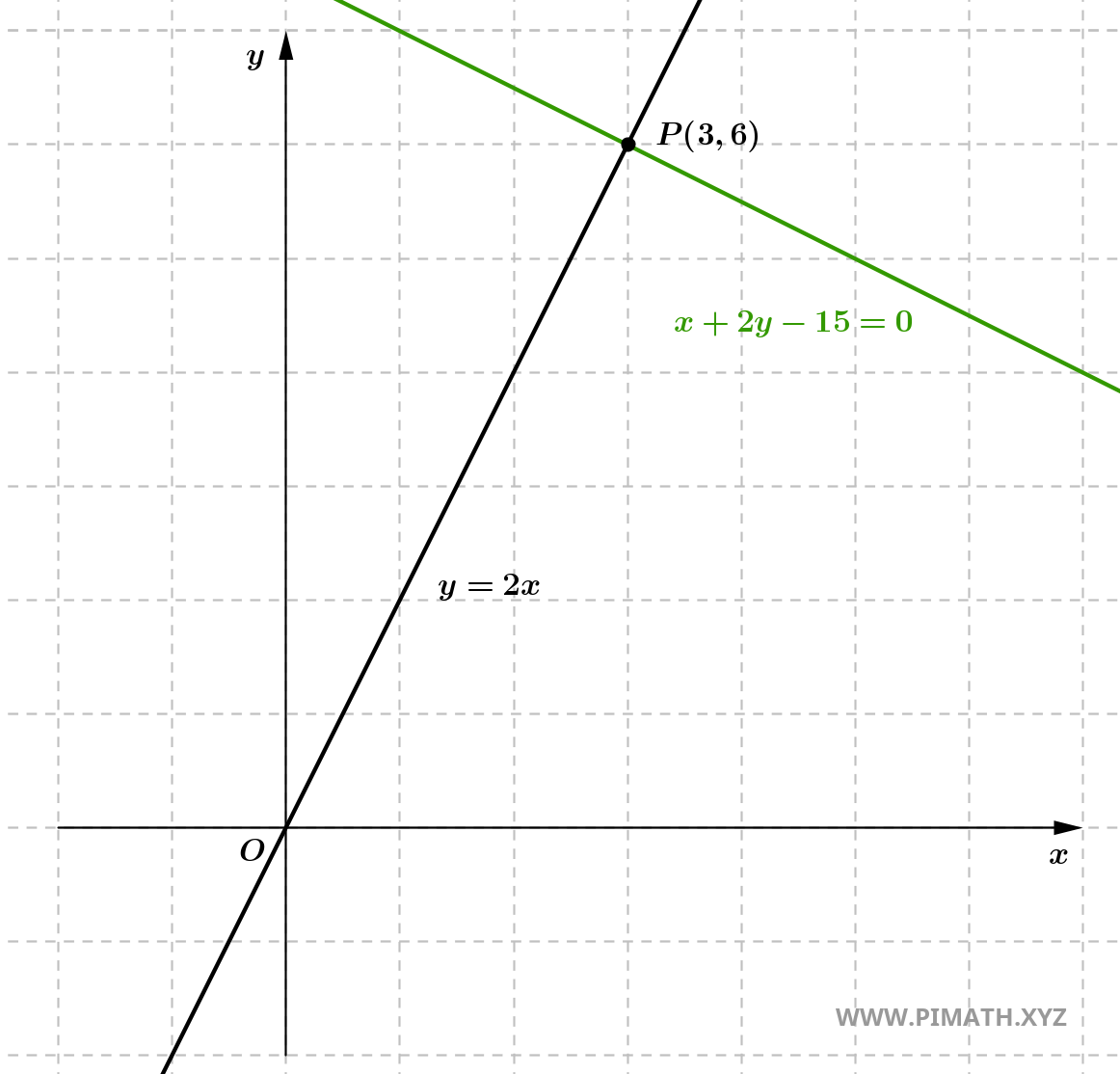
Ejercicio 2: Determina la recta perpendicular a \( y = 2x \) que pasa por \( P(3, 6) \).
Solución. La pendiente es \( m = 2 \), así que:
\[ m_\perp = -\frac{1}{2}. \]
- Usamos punto-pendiente: \[ y - 6 = -\frac{1}{2}(x - 3). \]
- Desarrollamos: \[ y = -\frac{1}{2}x + \frac{15}{2}. \]
Forma implícita:
\[ x + 2y - 15 = 0. \]
Verificación:
- \( y = -\frac{1}{2} \cdot 3 + \frac{15}{2} = 6 \)
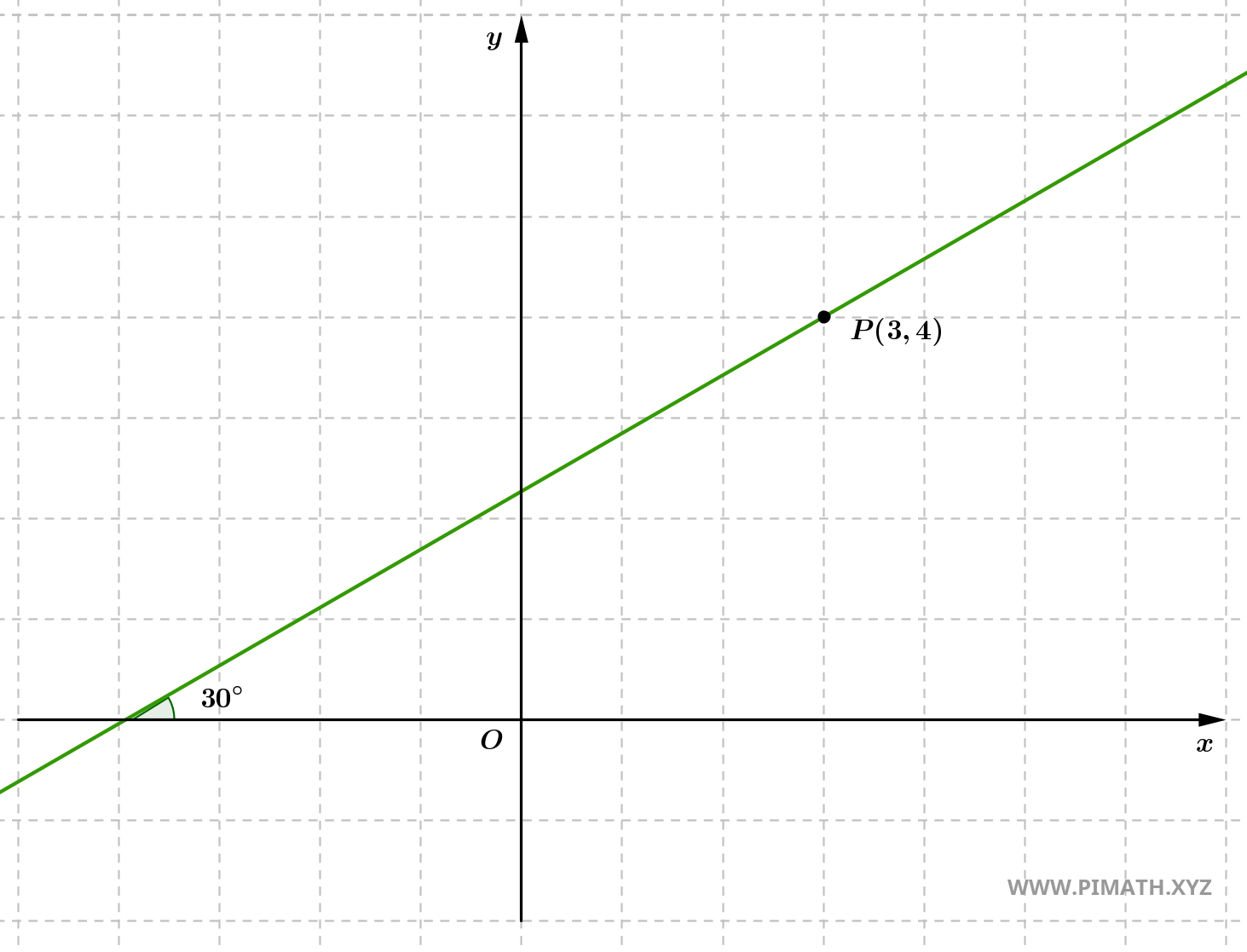
Ejercicio 3: Encuentra la recta que pasa por \( P(3, 4) \) y forma un ángulo de \( 30^\circ \) con el eje \( x \).
Solución. La pendiente es:
\[ m = \tan(30^\circ) = \frac{1}{\sqrt{3}}. \]
- Usamos punto-pendiente: \[ y - 4 = \frac{1}{\sqrt{3}}(x - 3). \]
- Simplificamos: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Verificación: Sustituimos \( x = 3 \), se obtiene \( y = 4 \).
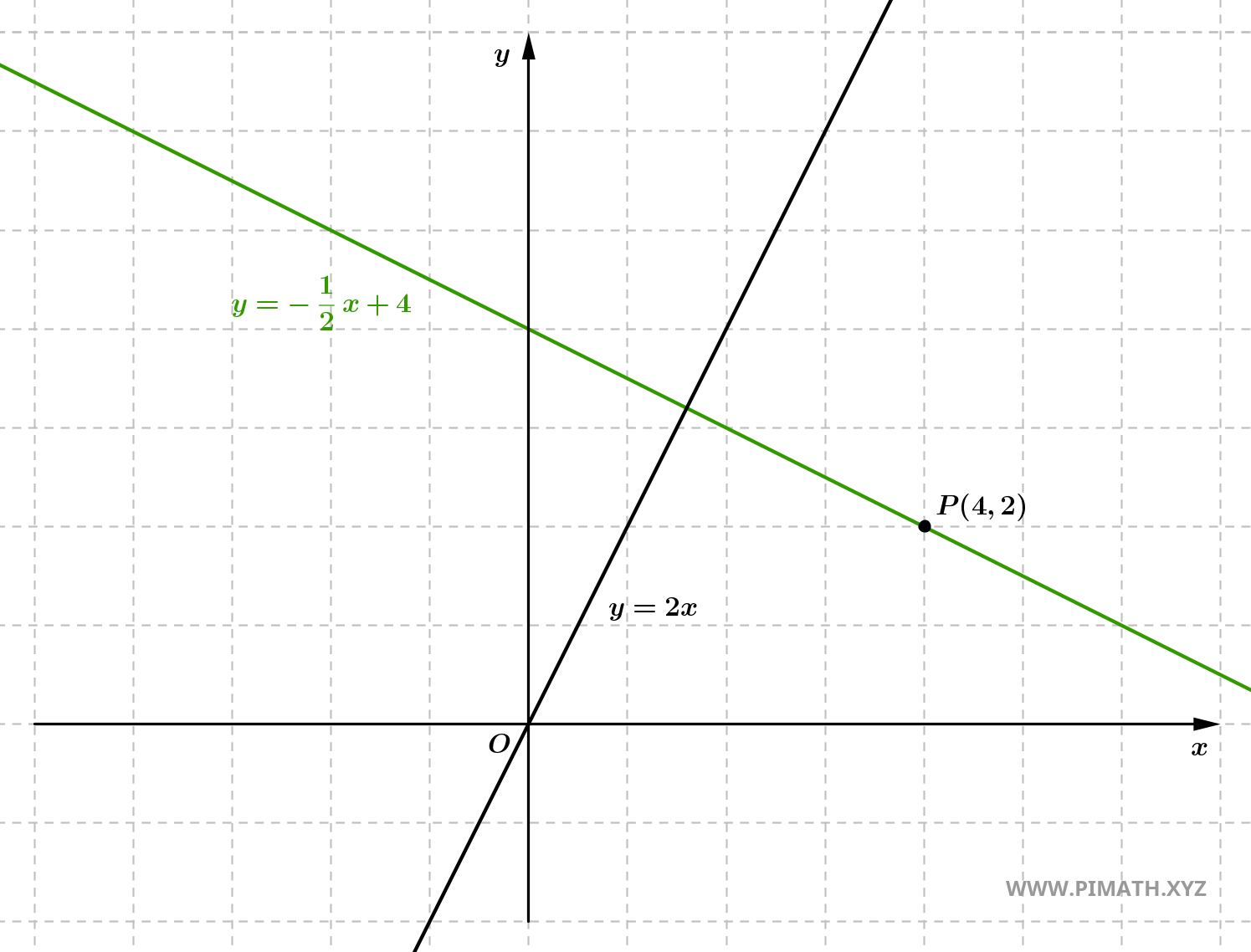
Ejercicio 4: Determina la recta perpendicular a \( y = 2x \) que pasa por \( P(4, 2) \).
Solución. Pendiente perpendicular:
\[ m_\perp = -\frac{1}{2}. \]
- Ecuación: \[ y - 2 = -\frac{1}{2}(x - 4). \]
- Simplificamos: \[ y = -\frac{1}{2}x + 4. \]
Forma implícita: \[ x + 2y - 8 = 0. \]
Verificación: Con \( x = 4 \), se obtiene \( y = 2 \).
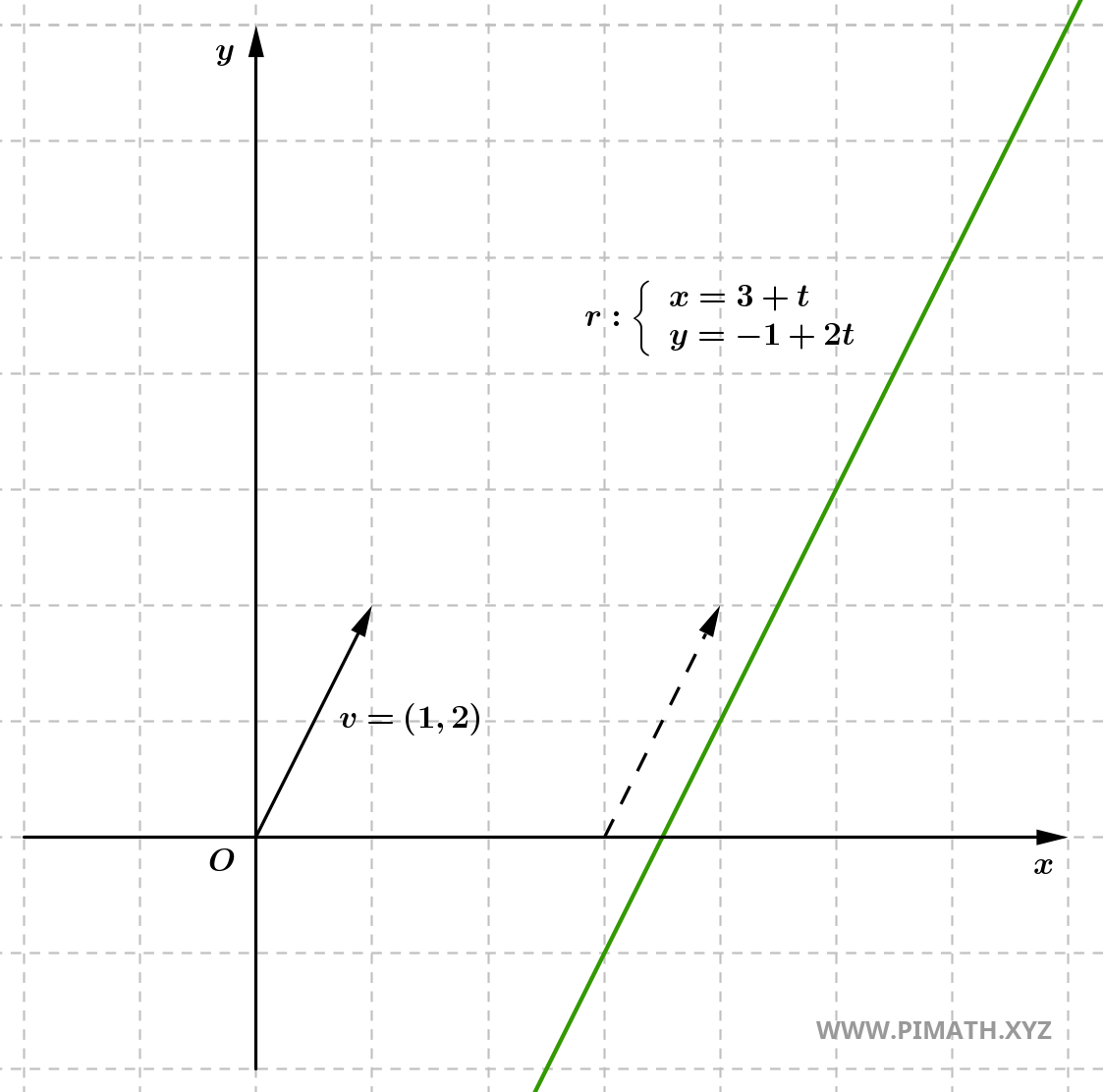
Ejercicio 5: Escribe la ecuación paramétrica de la recta que pasa por \( A(3, -1) \) y \( B(4, 1) \), y luego su forma cartesiana.
Solución. Vector director:
\[ \vec{v} = (1,\ 2). \]
Ecuación paramétrica:
\[ \begin{cases} x = 3 + t \\ y = -1 + 2t \end{cases} \quad t \in \mathbb{R}. \]
Forma cartesiana:
\[ t = x - 3 \quad \Rightarrow \quad y = 2x - 7. \]
Forma implícita: \[ 2x - y - 7 = 0. \]