Una ecuación de primer grado es un polinomio de primer grado igualado a cero. En general, una ecuación es de primer grado si puede escribirse en la forma canónica:
\[ ax + b = 0 \quad \text{con} \quad a \neq 0 \]
La parte que está a la izquierda del signo de igualdad se llama primer miembro, mientras que la que está a la derecha se llama segundo miembro.
Índice
- Cómo resolver una ecuación de primer grado
- Primer principio de equivalencia
- Segundo principio de equivalencia
- Ejercicios Resueltos
- Errores comunes que evitar
- Significado Geométrico
Cómo resolver una ecuación de primer grado
Resolver una ecuación de primer grado significa encontrar el valor que, sustituido en la incógnita \( x \), satisface la ecuación. Esto equivale a decir que el valor (solución de la ecuación) debe hacer verdadera la igualdad. El proceso de resolución comprende ciertos pasos, llamados principios de equivalencia para ecuaciones.
Primer principio de equivalencia
El primer principio de equivalencia establece que, sumando o restando a ambos miembros de una ecuación una cantidad o una expresión algebraica, el conjunto de soluciones no cambia.
Gracias a este principio, podemos restar la cantidad \( -b \) a ambos miembros:
\[ ax = -b \]
Observa que sumar o restar una cantidad a ambos miembros equivale a "pasar" de un miembro al otro siempre que se cambie el signo. Por ahora hemos pasado al segundo miembro \( b \) cambiado de signo, es decir \( -b \).
Segundo principio de equivalencia
El segundo principio de equivalencia establece que, multiplicando o dividiendo por un mismo número distinto de cero, el conjunto de soluciones de la ecuación no cambia.
Aplicando este principio a la ecuación equivalente \( ax = -b \), es decir, dividiendo por el número \( a \neq 0 \) a ambos miembros, obtenemos:
\[ x = -\frac{b}{a} \]
Es importante subrayar que \( a \) debe ser distinto de cero para que la ecuación tenga sentido. En efecto, si \( a = 0 \) la ecuación se convertiría en \( 0 \cdot x + b = 0 \) y por tanto \( b = 0 \), lo que no representa una ecuación en \( x \) y sería imposible si \( b \neq 0 \).
De ahora en adelante el objetivo será aislar la variable \( x \) en el primer miembro, o en el segundo (no cambia nada).
Ejercicios Resueltos
Ejercicio 1. Resolver la ecuación \( 3x - 1 = 0\).
Solución. Pasamos \( -1 \) al segundo miembro (cambiándole el signo):
\[ 3x = 1 \]
Finalmente, dividiendo ambos miembros por \( 3 \) obtenemos la solución buscada:
\[ x = \frac{1}{3} \]
Comprobación. Para verificar que es la solución correcta, sustituimos el valor encontrado en la ecuación de partida. Obtenemos:
\[ 3 \cdot \frac{1}{3} - 1 = 1 - 1 = 0 \]
Por tanto, la solución es correcta.
Ejercicio 2: Resolver la ecuación de primer grado \(\displaystyle\frac{1}{2}(x-1)=-x+1\).
Solución. Comenzamos aislando la incógnita \( x \) en el primer miembro:
\[ \frac{1}{2}(x - 1) = -x + 1 \implies \frac{x}{2} - \frac{1}{2} = -x + 1 \]
Ahora sumamos \(x\) a ambos miembros de la ecuación:
\[ \frac{x}{2} + x - \frac{1}{2} = 1 \]
Simplificamos transformando \(x\) en un término con denominador común:
\[ \frac{x}{2} + \frac{2x}{2} - \frac{1}{2} = 1 \implies \frac{3x}{2} - \frac{1}{2} = 1 \]
Sumamos \(\displaystyle\frac{1}{2}\) a ambos miembros:
\[ \frac{3x}{2} = \frac{3}{2} \]
Ahora multiplicamos ambos miembros por \(\displaystyle\frac{2}{3}\) para resolver para \(x\):
\[ x = 1 \]
Por tanto, la solución es \( x = 1 \).
Comprobación. Como antes, sustituimos \( x = 1 \) en la ecuación de partida:
\[ \frac{1}{2}(x - 1) = -x + 1 \]
Cuando \( x = 1 \), obtenemos:
\[ \frac{1}{2}(1 - 1) = -1 + 1 \]
Calculamos ambos miembros:
\[ \frac{1}{2} \cdot 0 = 0 \quad \text{y} \quad -1 + 1 = 0 \]
Los dos miembros son iguales, por tanto la solución es correcta.
Ejercicio 3. Resolver la ecuación \( 5(x - 2) - 3(2x + 1) = 7 - 4x \)
Solución. Aplicamos la propiedad distributiva:
\[ 5x - 10 - 6x - 3 = 7 - 4x \]
\[ -x - 13 = 7 - 4x \]
Pasamos los términos con \(x\) al primer miembro y los términos constantes al segundo miembro:
\[ -x + 4x = 7 + 13 \]
\[ 3x = 20 \]
Dividimos ambos miembros por 3:
\[ x = \frac{20}{3} \]
Comprobación. Sustituimos \(\displaystyle x = \frac{20}{3}\) en la ecuación de partida:
\[ 5\left(\frac{20}{3} - 2\right) - 3\left(2\cdot\frac{20}{3} + 1\right) = 7 - 4\cdot\frac{20}{3} \]
Calculamos el primer miembro:
\[ 5\left(\frac{20}{3} - \frac{6}{3}\right) - 3\left(\frac{40}{3} + \frac{3}{3}\right) = 5\cdot\frac{14}{3} - 3\cdot\frac{43}{3} = \frac{70}{3} - \frac{129}{3} = -\frac{59}{3} \]
Calculamos el segundo miembro:
\[ 7 - 4\cdot\frac{20}{3} = \frac{21}{3} - \frac{80}{3} = -\frac{59}{3} \]
Los dos miembros son iguales, por tanto la solución está verificada:
\[ x = \frac{20}{3} \]
Errores comunes que evitar
Cuando se resuelven ecuaciones de primer grado, es importante prestar atención a algunos errores frecuentes:
Error en el cambio de signo: Cuando se mueve un término de un miembro al otro, hay que recordar cambiarle el signo. Por ejemplo, en la ecuación \(2x + 3 = 5\), moviendo el \( 3 \) se obtiene \(2x = 5 - 3\) y no \(2x = 5 + 3\).
Distribución incompleta: Cuando se tiene una expresión del tipo \(3(x + 2)\), el coeficiente \( 3 \) debe multiplicarse por todos los términos dentro del paréntesis. Un error común es escribir \(3x + 2\) en lugar del correcto \(3x + 6\).
Errores con fracciones: Cuando se tiene una ecuación como \(\displaystyle \frac{x}{2} = 3\), para aislar \(x\) hay que multiplicar ambos miembros por 2, obteniendo \(x = 6\). Es incorrecto escribir \(x = \displaystyle \frac{3}{2}\).
Simplificación imprecisa: En una ecuación como \(2x - x = 5\), no hay que olvidar simplificar los términos semejantes antes de proceder. La forma correcta es \(x = 5\).
Comprobación ausente: Saltarse el paso de la comprobación puede llevar a no darse cuenta de eventuales errores de cálculo. Es siempre aconsejable sustituir la solución encontrada en la ecuación original para confirmar que sea correcta.
Significado Geométrico
Resolver una ecuación de primer grado \( ax + b = 0\) significa encontrar el valor en correspondencia del cual la recta de ecuación
\[ y = ax + b \]
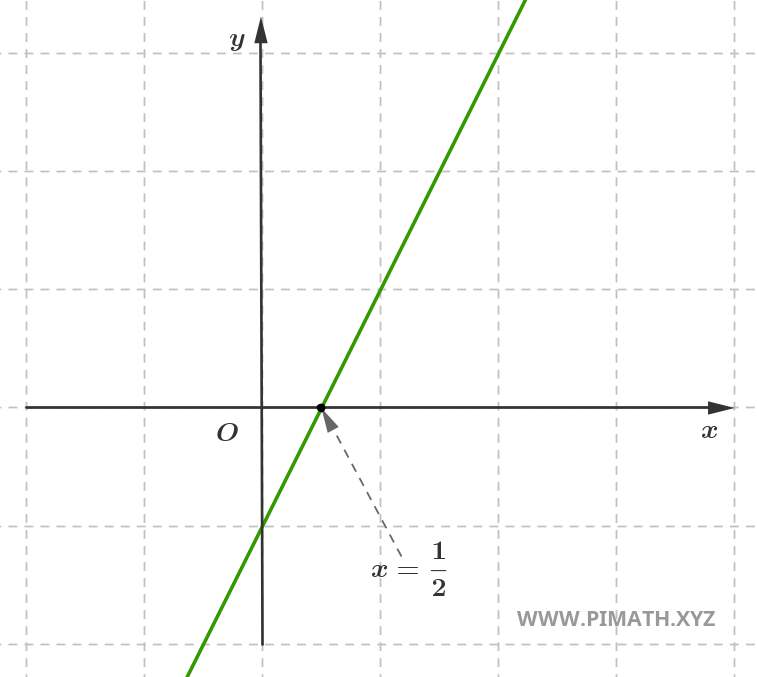
interseca el eje de las abscisas (eje \( x \)). Por ejemplo, la recta de ecuación \( y = 2x - 1 \)
interseca el eje de las abscisas en el punto \( x = \displaystyle \frac{1}{2} \), como se muestra en la figura.
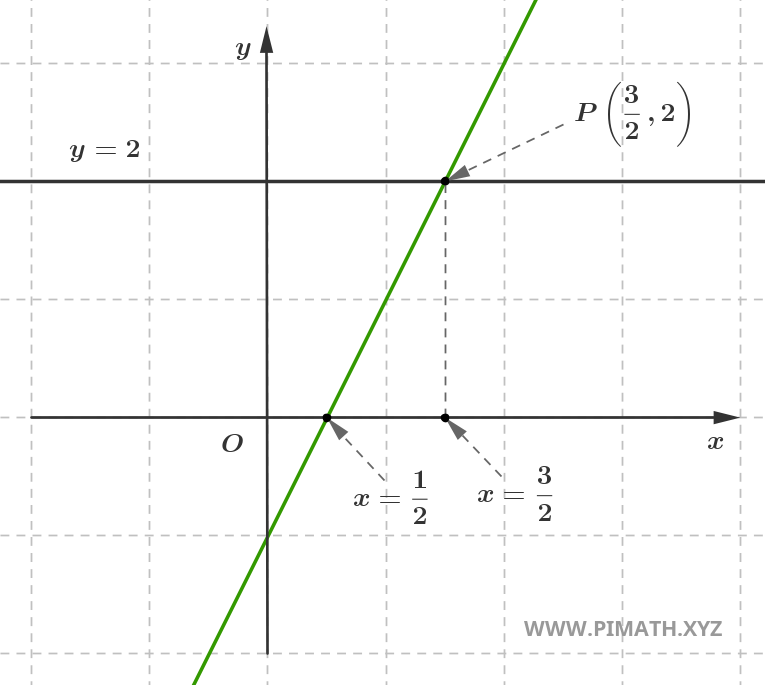
Hemos dicho que la solución de una ecuación de primer grado \( ax + b = 0 \) es la abscisa en la que la recta interseca con el eje \(x\). Ahora, planteémonos otra pregunta: ¿cómo podemos determinar el valor de \( x \) para el cual la recta \( y = ax + b \) asume un valor específico, por ejemplo \( y = 2 \)?
Para hacer esto, basta imponer \( y = 2 \) en la ecuación de la recta. Obtenemos así \( 2 = 2x - 1 \iff 2x - 3 = 0 \), por tanto:
\[ x=\frac{3}{2} \]
Como se muestra en la figura, a la solución que hemos encontrado corresponde la ordenada \(y=2\).