Las funciones pares y funciones impares se distinguen por sus simetrías: las funciones pares son simétricas respecto al eje de ordenadas, mientras que las funciones impares lo son respecto al origen. También profundizaremos en el comportamiento de la suma de funciones: la suma de dos funciones pares sigue siendo una función par, así como la suma de dos funciones impares sigue siendo impar. Finalmente, veremos cómo descomponer una función en su parte par y su parte impar.
- Funciones Pares
- Suma de dos funciones pares
- Funciones Impares
- Suma de dos funciones impares
- Funciones que no son ni pares ni impares
- Integración sobre intervalos simétricos
- Descomposición de una función en parte par y parte impar
- Demostración de la unicidad de la descomposición
Funciones Pares
Definición. Una función \( f : X \to Y \) se dice par si:
\[ \forall x \in X, \quad -x \in X \quad \text{y} \quad f(-x) = f(x) \]
En otras palabras, la función es par si el dominio es simétrico respecto al origen y la función toma el mismo valor en \( x \) y \( -x \).
Ejemplo. La función \( f(x) = x^2 \) es par, ya que para todo \( x \in \mathbb{R} \), se tiene \( (-x)^2 = x^2 \).
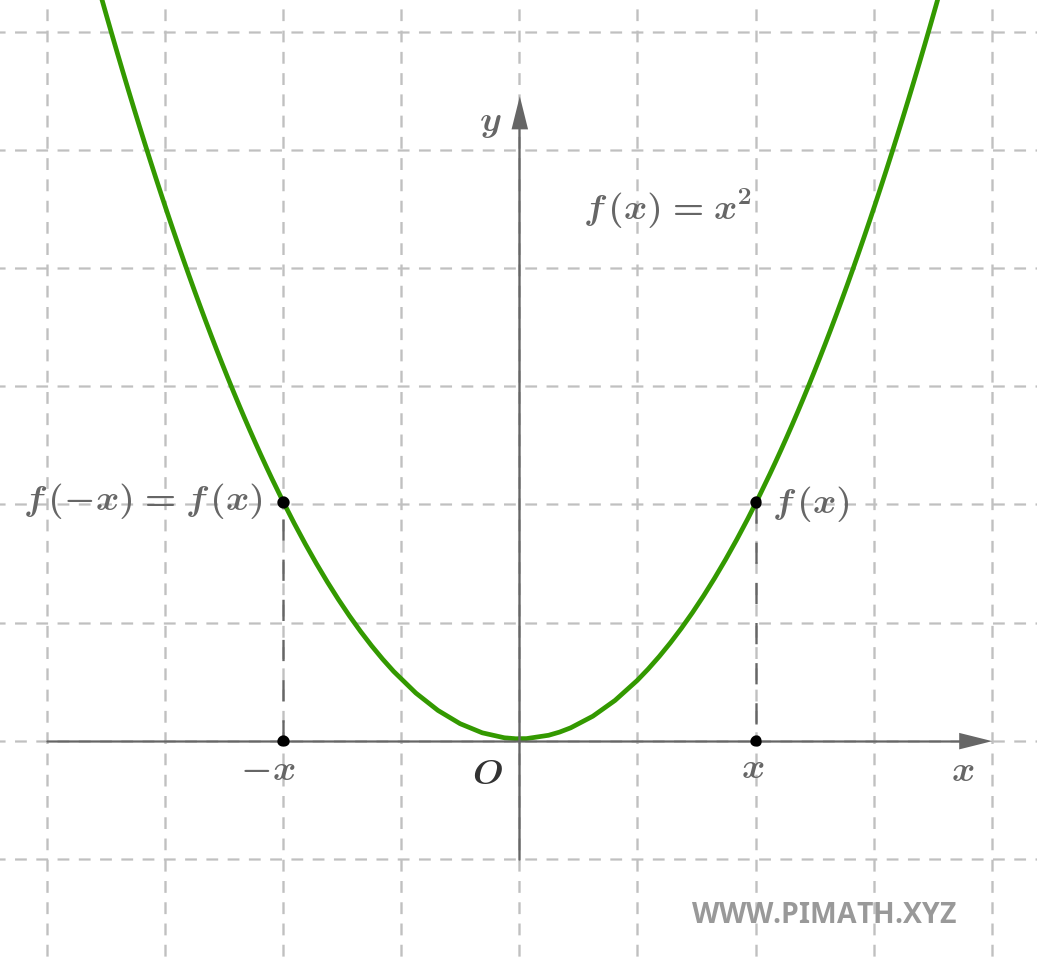
Ejemplo. La función \( f(x) = \cos(x) \) es par, ya que para todo \( x \in \mathbb{R} \), se tiene \( \cos(-x) = \cos(x) \).
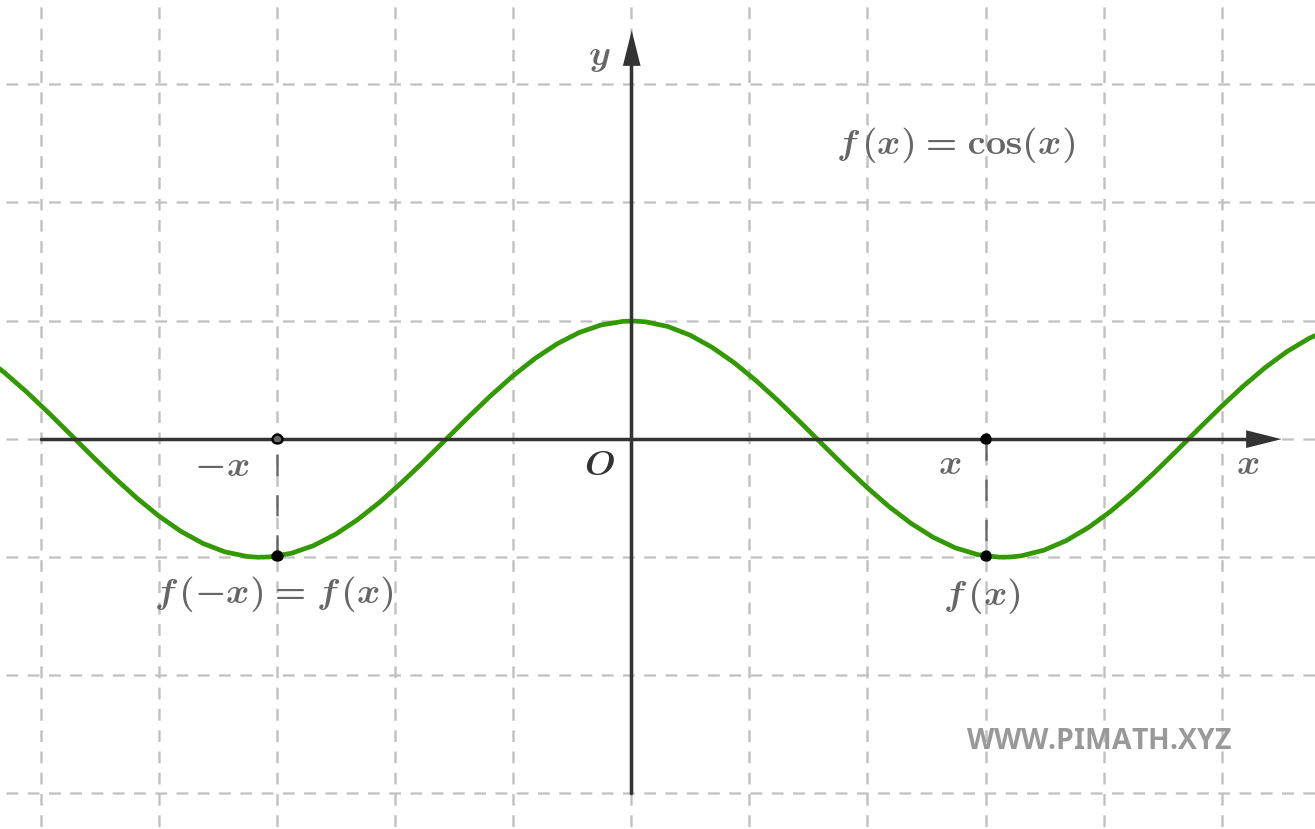
Ejemplo. La función \( f(x) = \cosh(x) \) es par, ya que para todo \( x \in \mathbb{R} \), se tiene \( \cosh(-x) = \cosh(x) \).
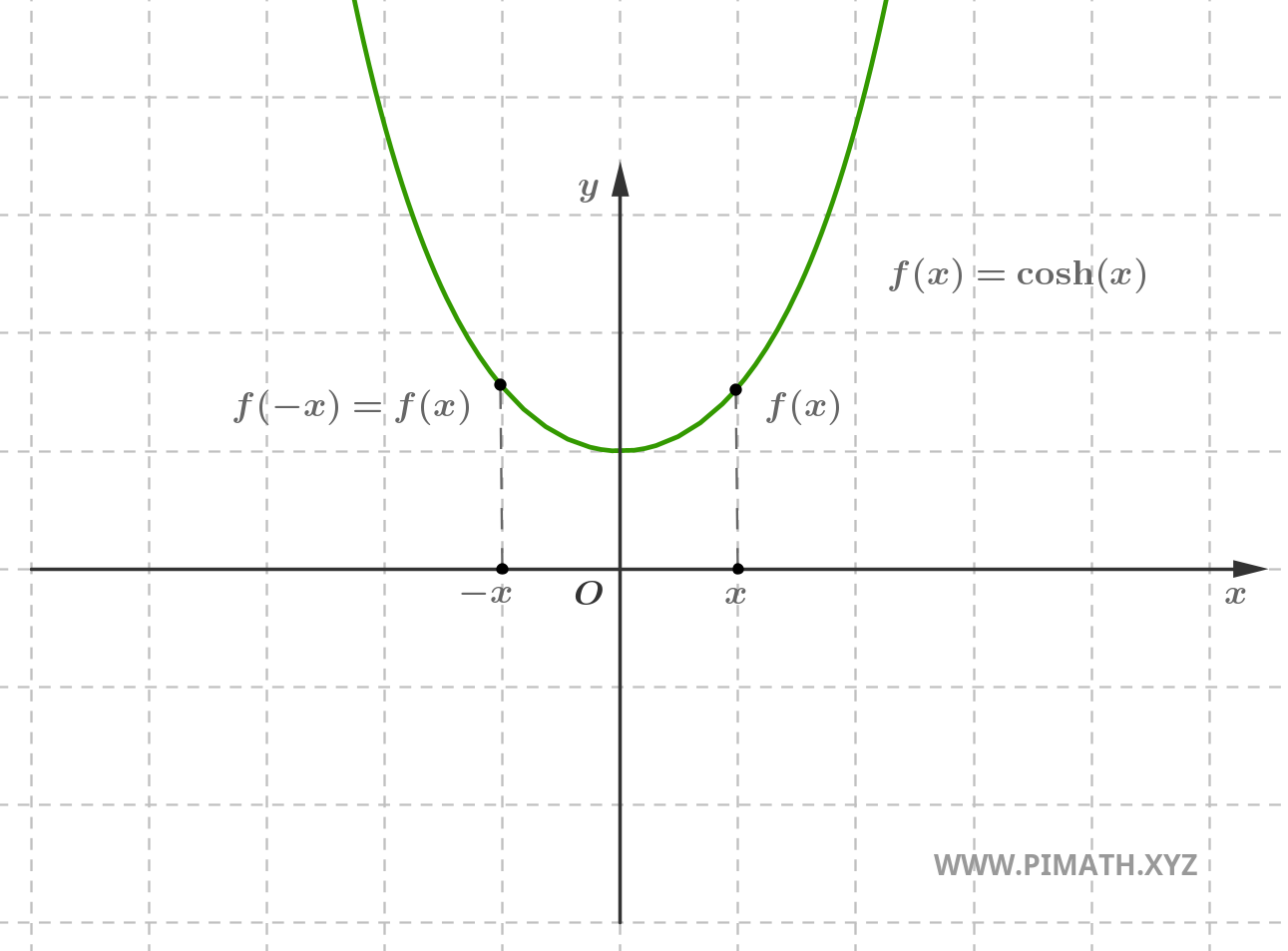
Ejemplo. La función \( f(x) = e^{-x^2} \) es par, ya que para todo \( x \in \mathbb{R} \), se tiene \( e^{-(-x)^2} = e^{-x^2} \).
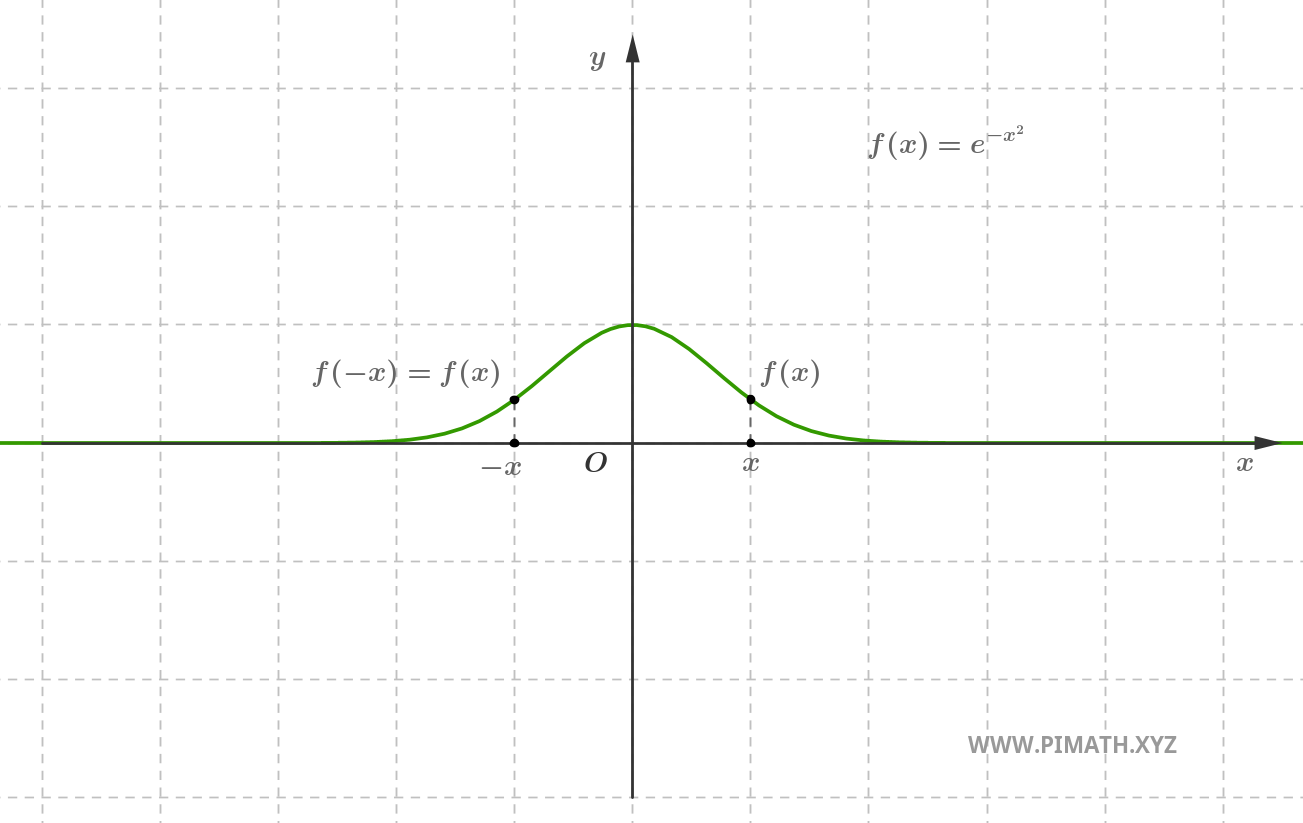
Suma de dos funciones pares
Sean \( f \) y \( g \) dos funciones pares, definidas respectivamente en \( D_f \) y \( D_g \). Consideremos la función suma \( f + g \), definida en el dominio \( D = D_f \cap D_g \). Puesto que \( D_f \) y \( D_g \) son simétricos, también la intersección \( D \) es simétrica. Para todo \( x \in D \), tenemos:
\[ (f + g)(-x) = f(-x) + g(-x) = f(x) + g(x) = (f + g)(x) \]
por tanto \( f + g \) es una función par.
Una función par presenta simetría respecto al eje de ordenadas. Por tanto, para analizar su gráfico, es suficiente estudiarla para \( x \geq 0 \); el tramo para \( x < 0 \) se obtiene por simetría.
Funciones Impares
Definición. Una función \( f : X \to Y \) se dice impar si:
\[ \forall x \in X, \quad -x \in X \quad \text{y} \quad f(-x) = -f(x) \]
En otras palabras, la función es impar si el dominio es simétrico respecto al origen y la función toma valores opuestos en \( x \) y \( -x \).
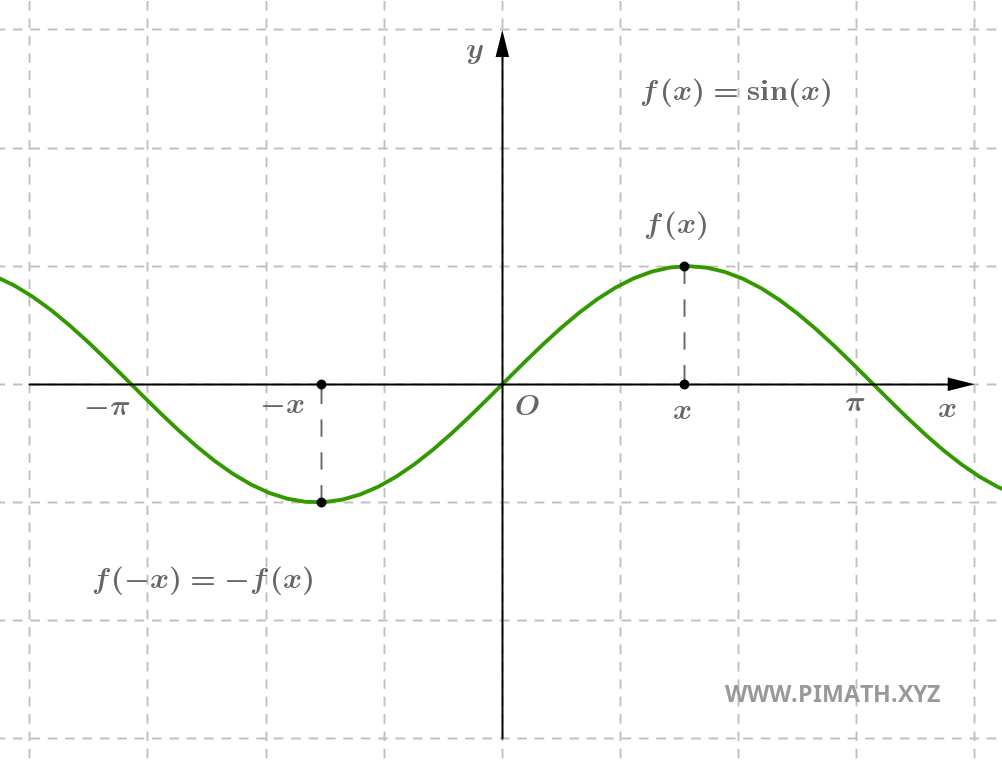
Ejemplo. La función \( f(x) = \sin(x) \) es impar, ya que para todo \( x \in \mathbb{R} \), se tiene \( \sin(-x) = -\sin(x) \).
Ejemplo. La función \( f(x) = x^3 \) es impar, ya que para todo \( x \in \mathbb{R} \), se tiene \( (-x)^3 = -x^3 \).
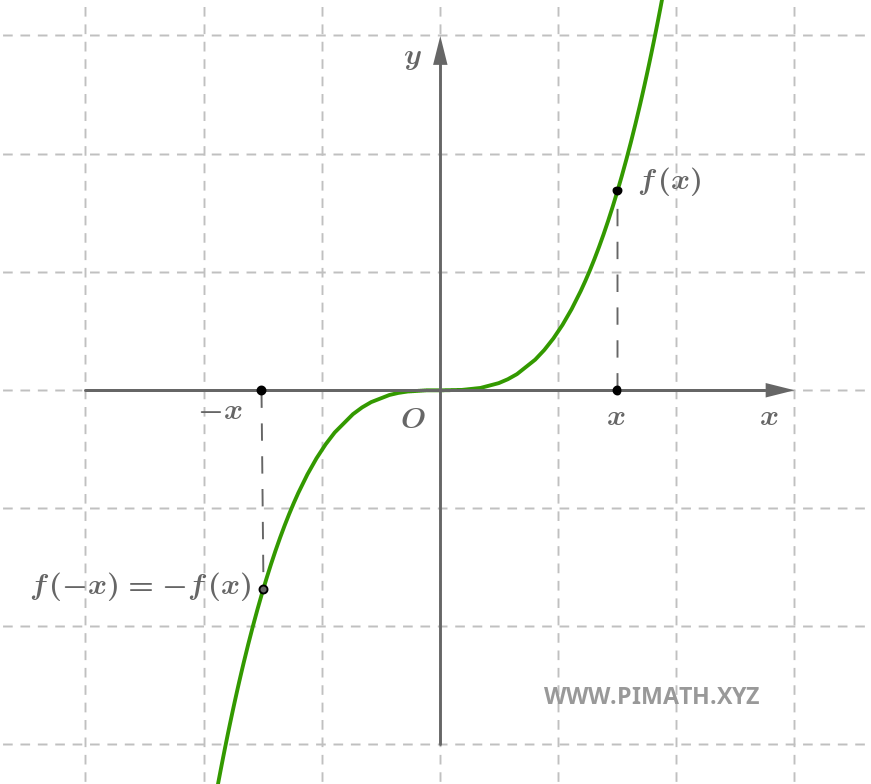
Una función impar es simétrica respecto al origen: al rotar su gráfico 180° alrededor del origen, se obtiene el mismo gráfico.
Suma de dos funciones impares
Sean \( f \) y \( g \) dos funciones impares, definidas en los dominios \( D_f \) y \( D_g \). Entonces la suma \( f + g \), definida en el dominio común \( D = D_f \cap D_g \), también es impar.
En efecto, para todo \( x \in D \), se cumple:
\[ (f + g)(-x) = f(-x) + g(-x) = -f(x) - g(x) = -(f(x) + g(x)) = -(f + g)(x) \]
Por tanto, \( f + g \) es una función impar.
Funciones que no son ni pares ni impares
Si una función no satisface ni la relación \( f(-x) = f(x) \), ni \( f(-x) = -f(x) \), entonces no es ni par ni impar.
Ejemplo. Las funciones \( f(x) = e^x \) y \( f(x) = x + 1 \) no son ni pares ni impares.
Integración sobre intervalos simétricos
Las funciones pares e impares son particularmente útiles en el cálculo de integrales definidas sobre intervalos simétricos respecto al origen.
Si \( f \) es par, entonces:
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
Si \( f \) es impar, entonces:
\[ \int_{-a}^{a} f(x) \, dx = 0 \]
Descomposición de una función en parte par y parte impar
Sea \( f : X \to \mathbb{R} \) una función definida en un conjunto simétrico respecto al origen, es decir, tal que \( x \in X \implies -x \in X \). En este caso, la función \( f \) puede escribirse de manera única como suma de una función par y de una función impar.
Concretamente, se definen:
\[ f_p(x) = \frac{f(x) + f(-x)}{2} \quad \text{(parte par de \( f \))} \]
\[ f_i(x) = \frac{f(x) - f(-x)}{2} \quad \text{(parte impar de \( f \))} \]
Es inmediato verificar que \( f_p(-x) = f_p(x) \) y \( f_i(-x) = -f_i(x) \), por tanto \( f_p \) es par y \( f_i \) es impar. Además, sumando las dos expresiones se obtiene:
\[ f(x) = f_p(x) + f_i(x) \]
es decir, toda función \( f \) (definida en un conjunto simétrico) se puede descomponer de manera única en la suma de una función par y una impar.
Ejemplo. Consideremos la función \( f(x) = e^x \), definida en todo \( \mathbb{R} \). La parte par es:
\[ f_p(x) = \frac{e^x + e^{-x}}{2} = \cosh x \]
mientras que la parte impar es:
\[ f_i(x) = \frac{e^x - e^{-x}}{2} = \sinh x \]
Se tiene entonces la descomposición:
\[ e^x = \cosh x + \sinh x \]
Observación: La descomposición es posible solo si el dominio de la función es simétrico respecto al origen. Además, la escritura \( f = f_p + f_i \) es única: existe una sola función par y una sola función impar cuya suma devuelve \( f \).
Demostración de la unicidad de la descomposición
Supongamos que una función \( f : X \to \mathbb{R} \), definida en un conjunto simétrico respecto al origen, se pueda escribir de dos maneras distintas como suma de una función par y de una función impar:
\[ f(x) = f_p(x) + f_i(x) = g_p(x) + g_i(x), \]
donde \( f_p \), \( g_p \) son pares y \( f_i \), \( g_i \) son impares.
Entonces:
\[ f_p(x) - g_p(x) = g_i(x) - f_i(x) \]
Llamemos \( h(x) = f_p(x) - g_p(x) = g_i(x) - f_i(x) \). La función \( h \) es por tanto par (como diferencia de dos funciones pares) e impar (como diferencia de dos funciones impares).
Pero si una función es simultáneamente par e impar, entonces:
\[ h(x) = h(-x) \quad \text{y} \quad h(x) = -h(-x) \implies h(x) = -h(x) \]
es decir, \( h(x) = 0 \) para todo \( x \in X \).
Por consiguiente, \( f_p(x) = g_p(x) \) y \( f_i(x) = g_i(x) \), lo que demuestra la unicidad de la descomposición.