Una inecuación de segundo grado es una expresión algebraica que establece una relación de orden entre dos términos que contienen una variable de segundo grado. Puede escribirse en la forma:
\[ a x^2 + bx + c \leq 0 \quad \text{o} \quad a x^2 + bx + c \geq 0 \]
donde \( a \) y \( b \) son coeficientes reales con \( a \neq 0 \) y \( x \) es la variable incógnita. Se habla de inecuación en sentido estricto si
\[ a x^2 + bx + c < 0 \quad \text{o} \quad a x^2 + bx + c > 0 \]
- Qué son las Inecuaciones de Segundo Grado
- Principios de Equivalencia para las Inecuaciones
- Cómo resolver las Inecuaciones de Segundo Grado
Qué son las Inecuaciones de Segundo Grado
Una inecuación de segundo grado establece una relación de orden entre dos expresiones algebraicas, y la solución está representada por un intervalo de valores que verifican la desigualdad. En otras palabras, el conjunto de soluciones de una inecuación de segundo grado no son dos valores, sino un intervalo o la unión de intervalos de números reales.
Principios de Equivalencia para las Inecuaciones de Segundo Grado
La resolución de una inecuación de segundo grado se basa en dos principios fundamentales:
Primer Principio de Equivalencia
El principio de equivalencia para las inecuaciones de segundo grado afirma que si se suma o resta el mismo número a ambos miembros de una inecuación, la relación de orden no cambia. Por ejemplo:
Si \( a x^2 + b x + c \leq 0 \), entonces podemos sumar \( d \) a ambos miembros y obtener:
\[ (a x^2 + b x + c) + d \leq 0 + d \]
Segundo Principio de Equivalencia
El segundo principio de equivalencia afirma que si se multiplica o divide ambos miembros de una inecuación por un número positivo, la relación de orden no cambia. Sin embargo, si se multiplica o divide por un número negativo, la inecuación debe invertirse. Estos son algunos ejemplos:
Si \( a x^2 + b x + c \leq 0 \) y multiplicamos ambos miembros por un número positivo \( k \), obtenemos:
\[ k(a x^2 + b x + c) \leq k \cdot 0 \]
Si, en cambio, multiplicamos por un número negativo \( k \), la inecuación se convierte en:
\[ k(a x^2 + b x + c) \geq k \cdot 0 \]
Cuando se multiplica o se divide ambos miembros de una inecuación de segundo grado por un número negativo, hay que invertir el signo de la inecuación. Por ejemplo:
Si \( -2 x^2 + 4 x \leq 6 \), dividiendo ambos miembros por \( -2 \), debemos invertir el signo de la inecuación:
\[ x^2 - 2 x \geq -3 \]
Cómo resolver las Inecuaciones de Segundo Grado
El primer paso consiste en reescribir la inecuación en forma canónica, por tanto llevamos todos los términos al primer miembro:
\[ ax^2+bx+c \leq 0 \quad \text{o} \quad ax^2+bx+c \geq 0 \]
\[ ax^2+bx+c < 0 \quad \text{o} \quad ax^2+bx+c > 0 \]
según se trate de una desigualdad o desigualdad en sentido estricto.
En este punto, debemos calcular las raíces (o soluciones) de la ecuación asociada, utilizando la fórmula resolutiva para las ecuaciones de segundo grado:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}, \quad \text{con} \quad \Delta = b^2 - 4ac \]
Las soluciones obtenidas nos permitirán determinar los intervalos en los que la inecuación se verifica, es decir, los valores de \(x\) para los cuales la inecuación se satisface, tanto dentro como fuera de dichos intervalos.
El signo del discriminante \( \Delta \) nos permite comprender la naturaleza de las soluciones: si \( \Delta > 0 \), hay dos soluciones reales distintas; si \( \Delta = 0 \), hay dos soluciones reales coincidentes; si \( \Delta < 0 \), no hay soluciones reales.
Resolución de la inecuación:
Si el coeficiente cuadrático de la ecuación asociada es mayor que cero, entonces las soluciones serán:
- \( (x_1, x_2) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c < 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1) \cup (x_2, +\infty) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c > 0 \quad , \quad a > 0 \]
- \( [x_1, x_2] \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c \leq 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c \geq 0 \quad , \quad a > 0 \]
En el caso de que el coeficiente cuadrático sea negativo (\(a < 0\)), los intervalos de solución se invertirán:
- \( (-\infty, x_1) \cup (x_2, +\infty) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c < 0 \quad , \quad a < 0 \]
- \( (x_1, x_2) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c > 0 \quad , \quad a < 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c \leq 0 \quad , \quad a < 0 \]
- \( [x_1, x_2] \) si la inecuación que queremos estudiar es
\[ ax^2+bx+c \geq 0 \quad , \quad a < 0 \]
Como veremos en la sección dedicada a la representación gráfica, no necesitarás aprender estas reglas de memoria.
Ejemplos Prácticos con Explicaciones Paso a Paso
Veamos algunos ejemplos de resolución de una inecuación de segundo grado.
Ejercicio 1. Encuentra los valores para los cuales la siguiente inecuación \( x^2 - 5x \leq -6 \) es verdadera.
Solución. Para resolver esta inecuación, seguimos los pasos fundamentales. Primero, llevamos todo al primer miembro para obtener la forma canónica:
\[ x^2 - 5x + 6 \leq 0 \]
Ahora calculamos el discriminante de la ecuación asociada. Considerando la expresión \( x^2 - 5x + 6 \), obtenemos:
\[ \Delta = (-5)^2 - 4(1)(6) = 25 - 24 = 1 \]
El discriminante es positivo, por lo que la ecuación tiene dos soluciones reales distintas. Resolviendo la ecuación asociada \( x^2 - 5x + 6 = 0 \), encontramos los valores:
\[ x_{1,2} = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2} \]
por tanto \( x_1 = 2 \) y \( x_2 = 3 \).
Puesto que el coeficiente del término \( x^2 \) es positivo, la parábola tiene la concavidad dirigida hacia arriba y la inecuación se satisfará en el intervalo comprendido entre las dos soluciones.
Las soluciones \( 2 \leq x \leq 3 \) pueden representarse gráficamente de la siguiente manera:
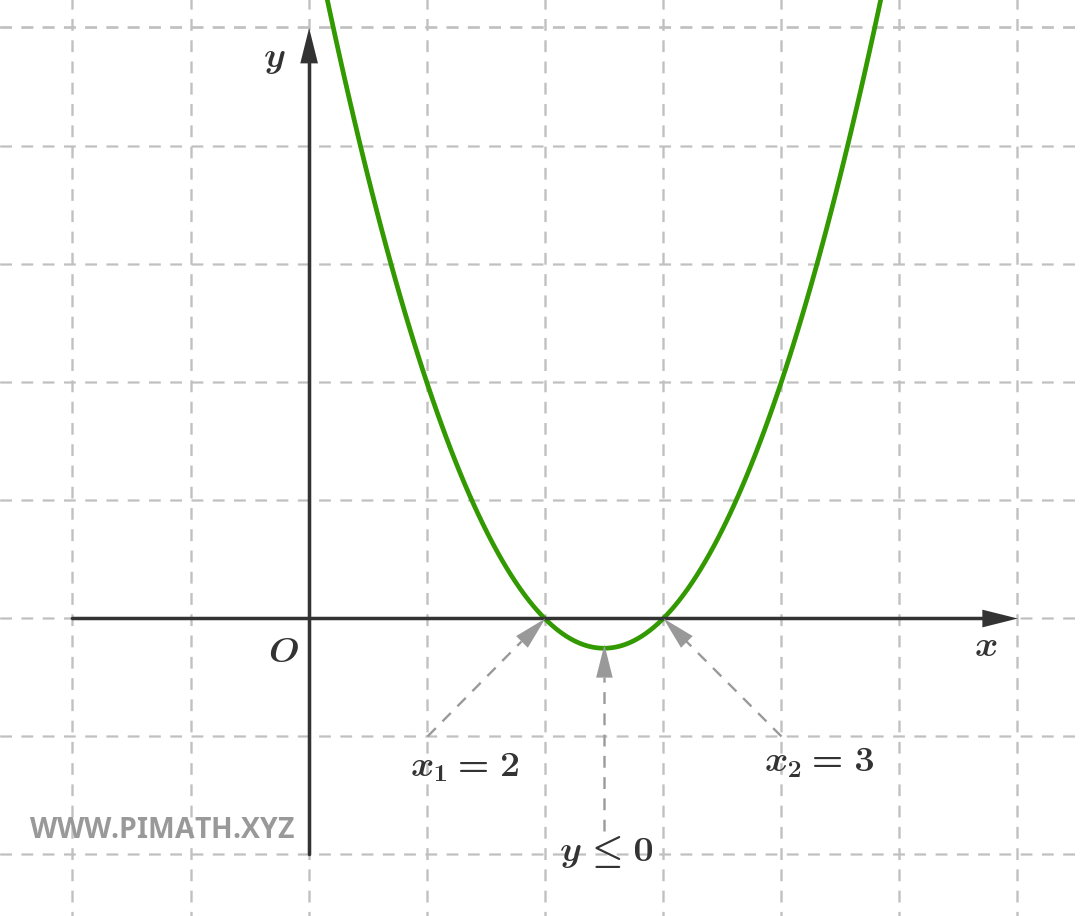
Normalmente, para evitar dibujar cada vez la parábola, se prefiere representar las soluciones en una recta, distinguiendo los valores positivos con una línea continua y los negativos con una línea punteada. Por ejemplo, las soluciones de la inecuación anterior se representan de esta manera:
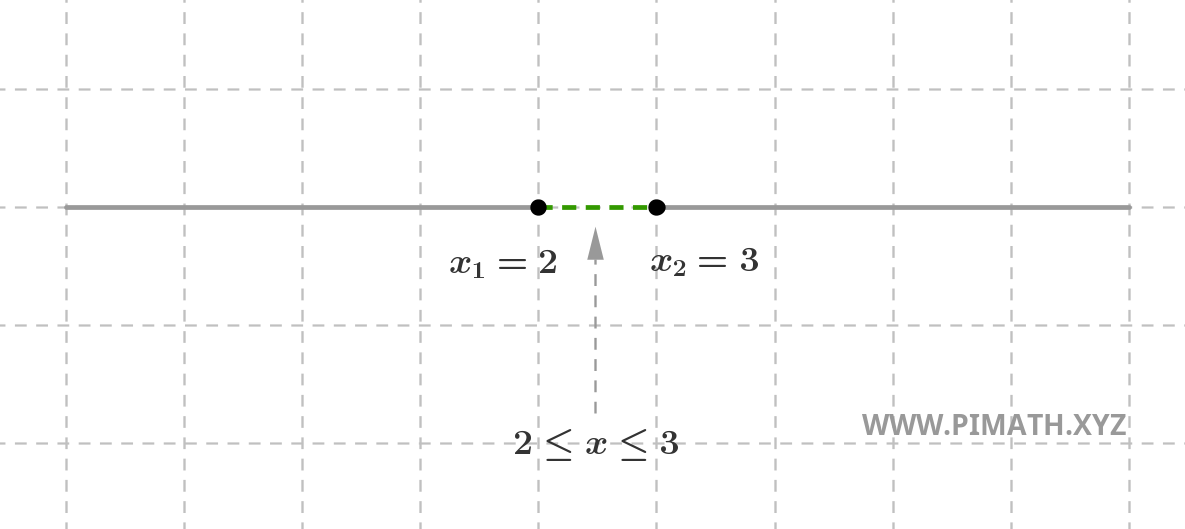
Atención a la inclusión de las soluciones: Si estamos estudiando una inecuación en sentido estricto (\( < \) o \( > \)), las raíces de la ecuación asociada deben excluirse, y esto se representa con círculos vacíos en la representación gráfica. Si en cambio la inecuación es en sentido amplio (\( \leq \) o \( \geq \)), las raíces se incluyen y se indican con círculos llenos.
Ejercicio 2. Resolver la inecuación de segundo grado \( 2x^2 - 4x - 6 > 0 \)
Solución. Calculamos el discriminante \( \Delta = b^2 - 4ac \)
Para esta ecuación, \( a = 2 \), \( b = -4 \), y \( c = -6 \). Sustituyendo estos valores en la fórmula:
\[ \Delta = (-4)^2 - 4(2)(-6) = 16 + 48 = 64 \]
Puesto que \( \Delta > 0 \), la ecuación tiene dos soluciones reales distintas.
La fórmula resolutiva para la ecuación asociada es:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} \]
Sustituyendo \( b = -4 \), \( \Delta = 64 \), y \( a = 2 \) en la fórmula:
\[ x_{1,2} = \frac{4 \pm \sqrt{64}}{2 \times 2} = \frac{4 \pm 8}{4} \]
La primera solución es \( x_1 = \displaystyle \frac{4 - 8}{4} = \displaystyle \frac{-4}{4} = -1 \), la segunda solución es en cambio \( x_2 = \displaystyle \frac{4 + 8}{4} = \displaystyle \frac{12}{4} = 3 \).
Las soluciones de la ecuación son por tanto:
\[ x_1 = -1 \quad \text{y} \quad x_2 = 3 \]
Observa que el coeficiente cuadrático es mayor que cero y la inecuación pide las soluciones para las cuales se tiene \( ax^2+bx+c > 0 \), por tanto las soluciones positivas se encuentran "externas al intervalo", es decir \( x < -1 \) o \( x > 3 \), como muestra el gráfico:
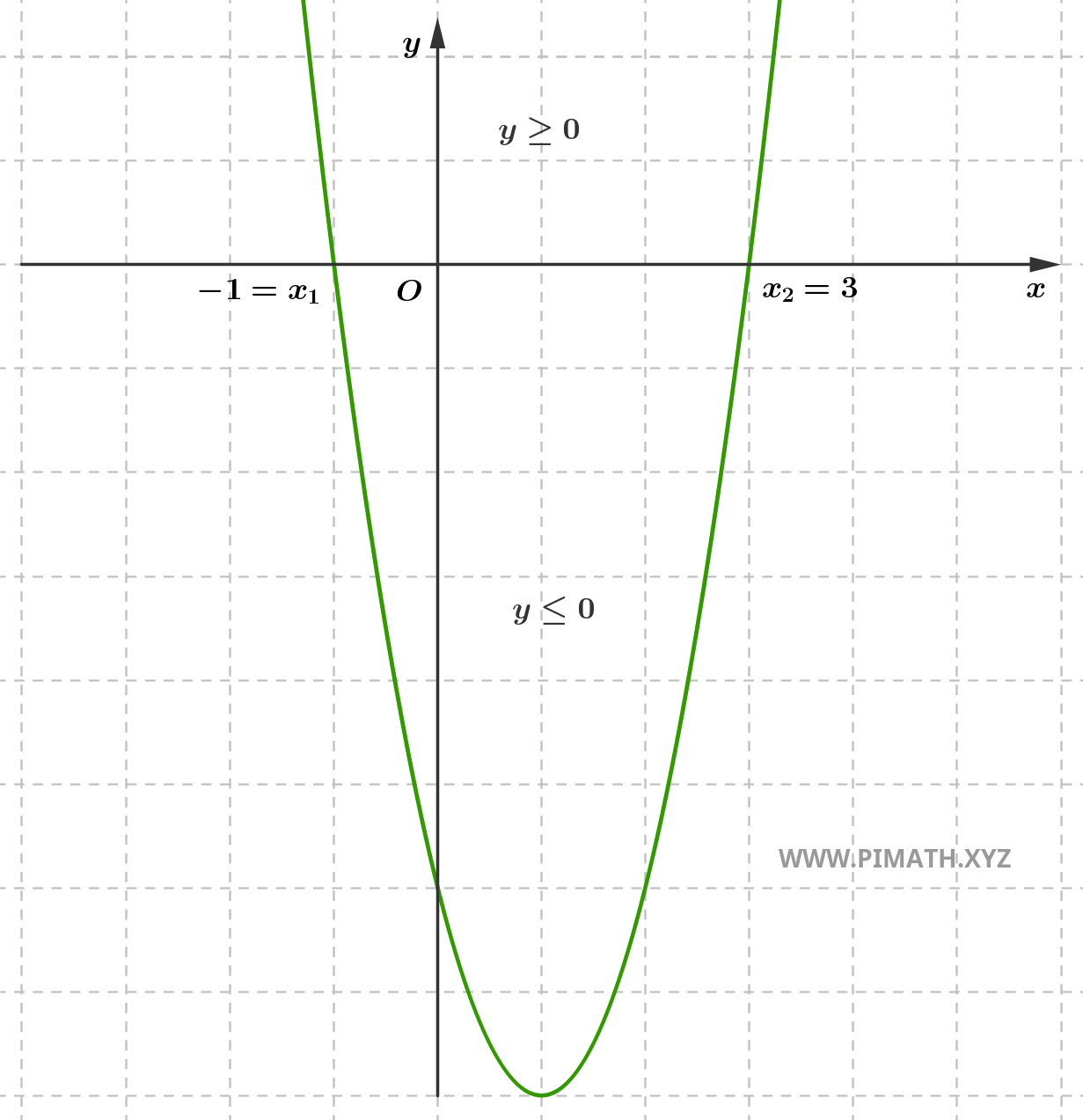
O bien:
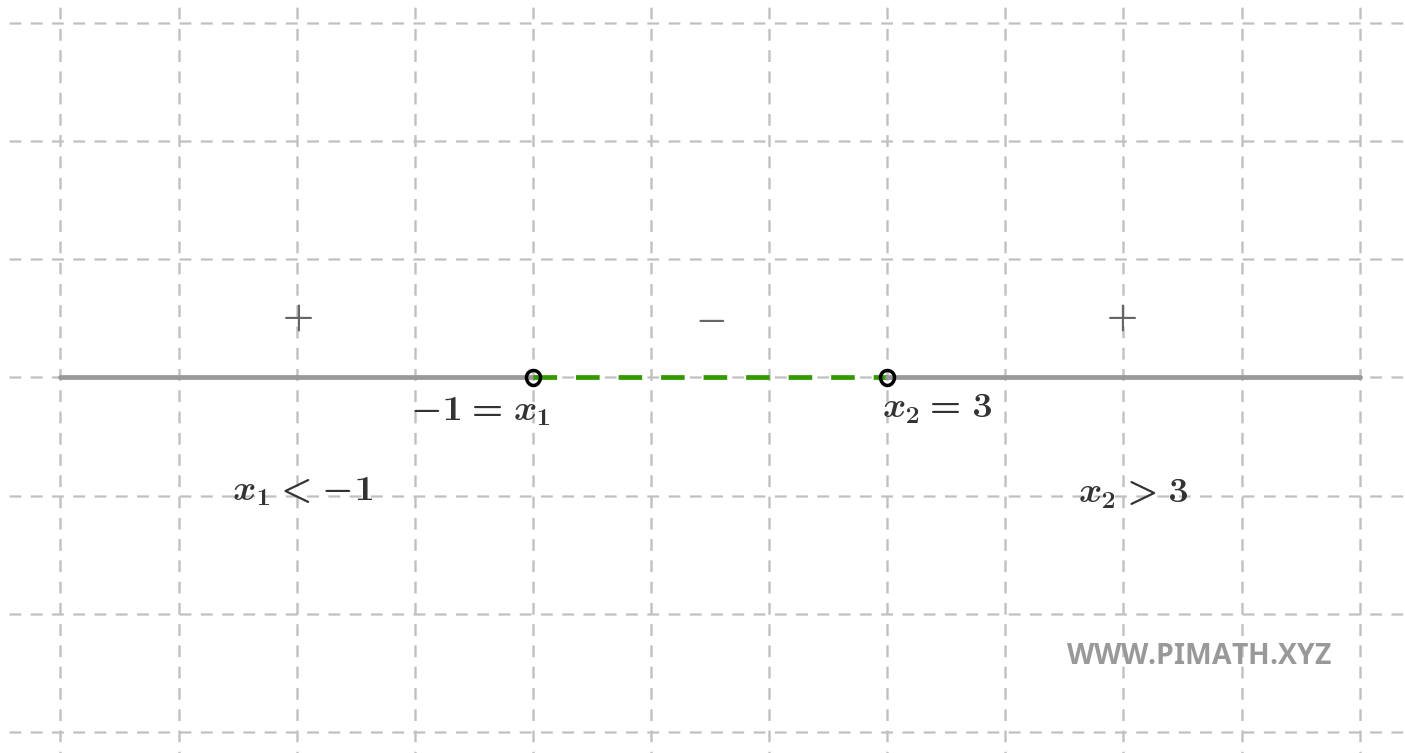
Observa, finalmente, que los círculos no están llenos ya que estamos excluyendo los puntos \( x = -1 \) y \( x = 3 \).
Ejercicio 3. Resolver la inecuación de segundo grado \( 2x^2+x+1 \leq 0 \).
Solución. La inecuación se presenta ya en forma canónica.
Calculamos el discriminante:
\[ \Delta = b^2 - 4ac \]
Sustituyendo \( a = 2 \), \( b = 1 \), \( c = 1 \):
\[ \Delta = (1)^2 - 4(2)(1) = 1 - 8 = -7 \]
Puesto que el discriminante es negativo, la ecuación asociada \( 2x^2+x+1 = 0 \) no tiene soluciones reales.
Además, puesto que el coeficiente del término cuadrático es positivo (\( a = 2 > 0 \)), la parábola tiene la concavidad dirigida hacia arriba, lo que significa que su valor es siempre positivo para cualquier valor de \( x \).
Para una inecuación en la forma \( 2x^2+x+1 \leq 0 \) con \( a > 0 \) y discriminante negativo, la inecuación no tiene soluciones, puesto que la función es siempre positiva y nunca puede ser menor o igual a cero.
Por tanto, la solución es el conjunto vacío. El gráfico de la función es:
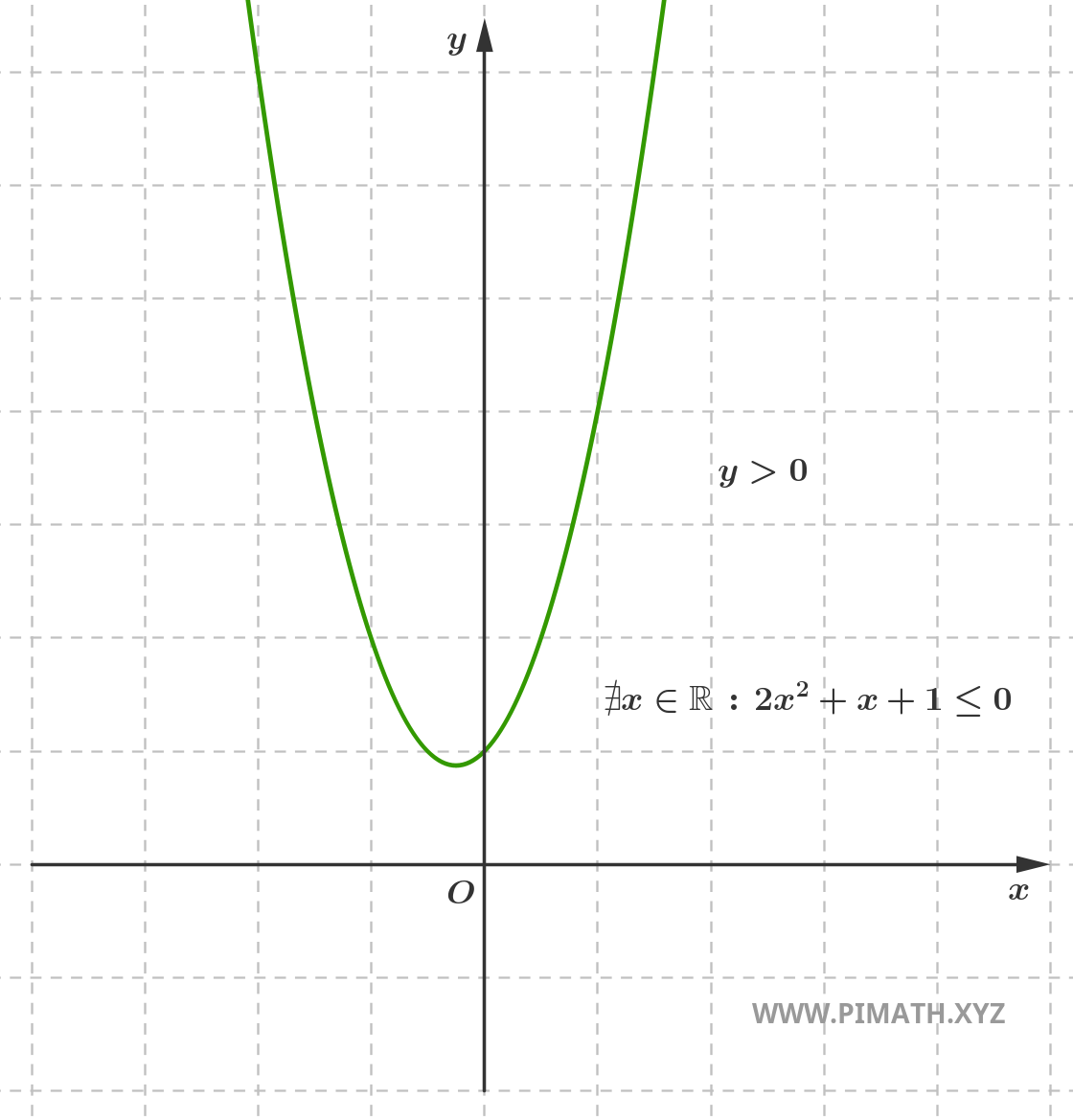
Como se puede observar, la parábola está siempre por encima del eje \( x \), por lo que no hay valores de \( x \) que satisfagan la inecuación \( 2x^2+x+1 \leq 0 \).

