Los límites notables son expresiones fundamentales en análisis matemático que describen el comportamiento local de las funciones en puntos críticos.
Estos límites son herramientas esenciales para establecer la continuidad, la diferenciabilidad y para simplificar el análisis del comportamiento asintótico de funciones más complejas.
- Demostración mediante el Criterio de Comparación
- Demostración mediante la regla de De L'Hôpital
- Demostración mediante la expansión en serie de Taylor
Demostración mediante el Criterio de Comparación
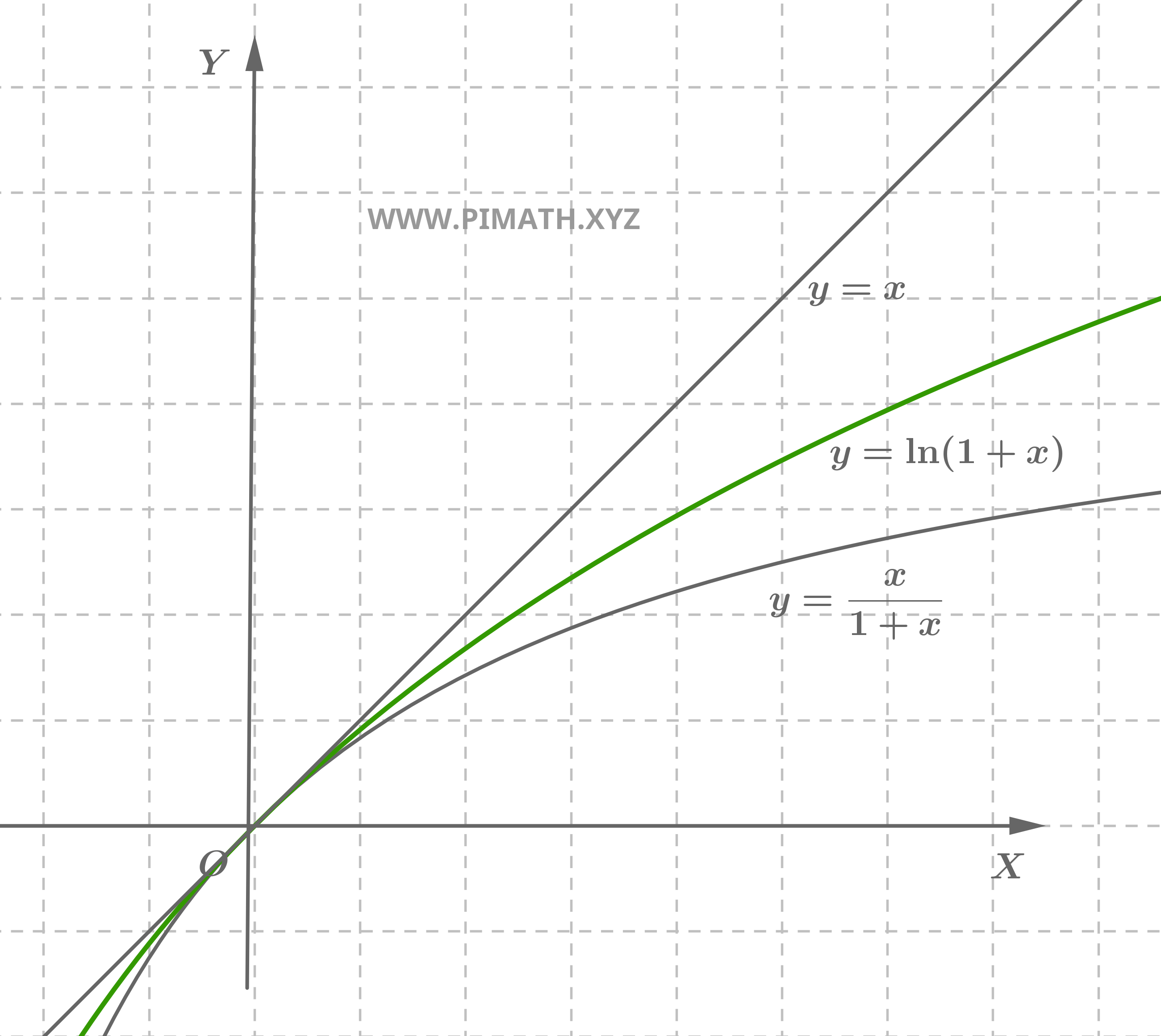
Consideremos el límite \[ \lim_{x \to 0} \frac{\ln(1+x)}{x}. \] Para \( x > 0 \) podemos utilizar las propiedades de concavidad de la función \(\ln(1+x)\). En particular, sabiendo que la función es cóncava, resulta que el gráfico de \(\ln(1+x)\) se sitúa por debajo de la tangente en \( x=0 \), es decir: \[ \ln(1+x) \leq x. \]
Además, se puede demostrar que para \( x > 0 \) también se cumple la siguiente desigualdad: \[ \ln(1+x) \geq \frac{x}{1+x}. \] Estas desigualdades se pueden resumir como: \[ \frac{x}{1+x} \leq \ln(1+x) \leq x. \]
Dividiendo por \( x \) (para \( x > 0 \)), obtenemos: \[ \frac{1}{1+x} \leq \frac{\ln(1+x)}{x} \leq 1. \]
Calculemos ahora los límites de los extremos cuando \( x \to 0 \): \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1 \quad \text{y} \quad \lim_{x \to 0} 1 = 1. \] Por el teorema del sándwich se concluye que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Por lo tanto, hemos demostrado por comparación que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
En este documento demostramos el siguiente límite notable:
Demostración mediante la regla de De L'Hôpital
Se observa que, al establecer \( f(x) = \ln(1+x) \) y \( g(x) = x \), cuando \( x \) tiende a cero se tiene \[ f(0) = \ln(1+0) = 0 \quad \text{y} \quad g(0) = 0, \] por lo que el límite toma la forma indeterminada \(\frac{0}{0}\). Esta condición nos permite aplicar la regla de De L'Hôpital.
Derivamos, entonces, el numerador y el denominador:
\[ f'(x) = \frac{d}{dx}\ln(1+x) = \frac{1}{1+x}, \quad g'(x) = \frac{d}{dx}x = 1. \]
Aplicando la regla de De L'Hôpital, obtenemos: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} = \lim_{x \to 0} \frac{1}{1+x}. \]
Dado que el límite \(\lim_{x \to 0} \frac{1}{1+x}\) se puede calcular inmediatamente, tenemos: \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1. \]
En consecuencia, se sigue que: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Demostración mediante la expansión en serie de Taylor
Alternativamente, podemos demostrar el resultado recurriendo a la expansión en serie de Taylor de la función \(\ln(1+x)\) alrededor de \( x=0 \):
La serie de Taylor de \(\ln(1+x)\) se da por: \[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots, \quad \text{para } |x| < 1. \]
Dividiendo por \( x \), se obtiene: \[ \frac{\ln(1+x)}{x} = 1 - \frac{x}{2} + \frac{x^2}{3} - \cdots. \]
Al hacer tender \( x \) a cero, todos los términos que contienen potencias positivas de \( x \) se anulan, dejando: \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Hemos demostrado, por lo tanto, que mediante tres métodos se tiene:
\[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
La primera demostración hizo uso del criterio de comparación, la segunda de la regla de De L'Hôpital, mientras que la tercera se basó en la expansión en serie de Taylor.

