La circunferencia es el lugar geométrico de los puntos del plano que están a una distancia constante de un punto fijo, llamado centro. Esta distancia constante se denomina radio. La circunferencia es una curva cerrada, simétrica respecto a su centro, y es un caso particular de cónica degenerada obtenida al seccionar un cono circular recto con un plano perpendicular al eje del cono.
Índice
- Definición Geométrica y Deducción de la Ecuación
- Ecuación de la Circunferencia con Centro en el Origen
- Ecuación de la Circunferencia con Centro Genérico
- Forma General y Completación de Cuadrados
- Condiciones para Representar una Circunferencia Real
- Posición de un Punto respecto a la Circunferencia
- Recta Tangente a la Circunferencia
- Intersección de Dos Circunferencias
- Haz de Circunferencias
- Simetrías y Propiedades Geométricas
- Ejercicios Resueltos
Definición Geométrica y Deducción de la Ecuación
Consideremos un punto fijo \( C(x_0, y_0) \) en el plano cartesiano ortogonal. La circunferencia de centro \( C \) y radio \( r > 0 \) es el conjunto de puntos \( P(x, y) \) del plano tales que:
\[ d = \text{dist}(P, C) = r \]
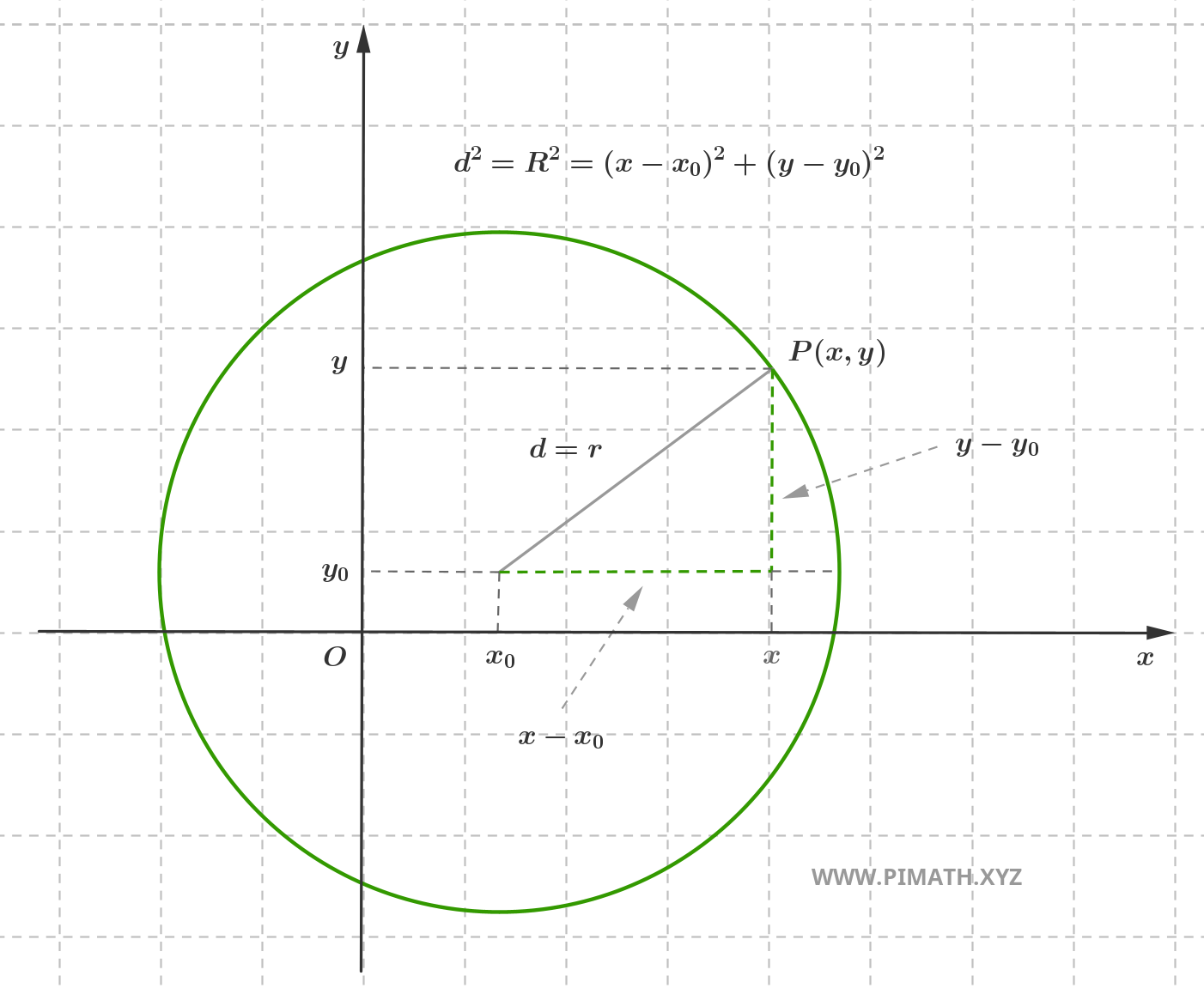
Aplicando la fórmula de la distancia euclidiana entre dos puntos en el plano cartesiano, se tiene:
\[ \text{dist}(P, C) = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]
Imponiendo la condición \( \text{dist}(P, C) = r \), obtenemos:
\[ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r \]
Elevando al cuadrado ambos miembros (operación válida puesto que ambos son no negativos, siendo \( r > 0 \) por definición):
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Esta es la forma canónica (o forma normal) de la ecuación de la circunferencia con centro \( C(x_0, y_0) \) y radio \( r \). La ecuación representa todos y solo aquellos puntos que satisfacen la condición geométrica de pertenencia a la circunferencia.
Ecuación de la Circunferencia con Centro en el Origen
En el caso particular en que el centro coincida con el origen del sistema de referencia, es decir \( C(0, 0) \), poniendo \( x_0 = 0 \) e \( y_0 = 0 \) en la forma canónica, la ecuación se simplifica notablemente:
\[ x^2 + y^2 = r^2 \]
Esta es la ecuación más elemental de la circunferencia y describe el conjunto de todos los puntos equidistantes del origen de los ejes cartesianos. La ecuación goza de las siguientes propiedades de simetría:
- Simetría respecto al eje de las abscisas: si \( (x, y) \) pertenece a la circunferencia, entonces también \( (x, -y) \) pertenece a ella
- Simetría respecto al eje de las ordenadas: si \( (x, y) \) pertenece a la circunferencia, entonces también \( (-x, y) \) pertenece a ella
- Simetría central respecto al origen: si \( (x, y) \) pertenece a la circunferencia, entonces también \( (-x, -y) \) pertenece a ella
Además, todos los diámetros de la circunferencia pasan por el origen y tienen longitud \( 2r \). El punto \( (r, 0) \) representa la intersección de la circunferencia con el semieje positivo de las abscisas.
Ecuación de la Circunferencia con Centro Genérico
Consideremos ahora el caso general de una circunferencia con centro en un punto arbitrario \( C(x_0, y_0) \) del plano y radio \( r > 0 \). La ecuación canónica es:
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Desarrollando los cuadrados de los binomios utilizando las identidades algebraicas \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \), obtenemos:
\[ x^2 - 2x \cdot x_0 + x_0^2 + y^2 - 2y \cdot y_0 + y_0^2 = r^2 \]
Reordenando los términos y llevando todas las cantidades al primer miembro:
\[ x^2 + y^2 - 2x_0 x - 2y_0 y + (x_0^2 + y_0^2 - r^2) = 0 \]
Introducimos ahora los parámetros:
\[ D = -2x_0 \quad , \quad E = -2y_0 \quad , \quad F = x_0^2 + y_0^2 - r^2 \]
De estas relaciones podemos obtener:
\[ x_0 = -\frac{D}{2} \quad , \quad y_0 = -\frac{E}{2} \quad , \quad r^2 = x_0^2 + y_0^2 - F = \frac{D^2 + E^2}{4} - F \]
Sustituyendo en la forma desarrollada, obtenemos la forma general de la ecuación de la circunferencia:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Forma General y Completación de Cuadrados
Dada una ecuación en la forma general:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
para reconducirla a la forma canónica y determinar centro y radio, utilizamos la técnica de la completación de cuadrados. El método consiste en transformar las expresiones \( x^2 + Dx \) e \( y^2 + Ey \) en cuadrados perfectos.
Para el término en \( x \):
\[ x^2 + Dx = x^2 + Dx + \frac{D^2}{4} - \frac{D^2}{4} = \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} \]
Análogamente, para el término en \( y \):
\[ y^2 + Ey = y^2 + Ey + \frac{E^2}{4} - \frac{E^2}{4} = \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} \]
Sustituyendo en la ecuación general:
\[ \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} + \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} + F = 0 \]
Reordenando:
\[ \left( x + \frac{D}{2} \right)^2 + \left( y + \frac{E}{2} \right)^2 = \frac{D^2 + E^2}{4} - F \]
Esta es la forma canónica, de la cual podemos leer directamente:
- Centro: \( C\left( -\displaystyle \frac{D}{2}, -\displaystyle\frac{E}{2} \right) \)
- Radio: \( r = \sqrt{\displaystyle\frac{D^2 + E^2}{4} - F} \) (siempre que la expresión bajo la raíz sea positiva)
Condiciones para Representar una Circunferencia Real
Una ecuación de la forma:
\[ ax^2 + by^2 + cxy + dx + ey + f = 0 \]
representa una circunferencia si y solo si se verifican las siguientes condiciones:
- Coeficientes de los términos cuadráticos iguales: \( a = b \neq 0 \)
- Ausencia del término mixto: \( c = 0 \)
- Discriminante positivo: \( \Delta = \displaystyle \frac{d^2 + e^2}{4a^2} - \displaystyle \frac{f}{a} > 0 \)
En el caso de la forma estándar \( x^2 + y^2 + Dx + Ey + F = 0 \), la condición se reduce a:
\[ \frac{D^2 + E^2}{4} - F > 0 \quad \Leftrightarrow \quad D^2 + E^2 - 4F > 0 \]
Distinguimos tres casos:
- Si \( D^2 + E^2 - 4F > 0 \): la ecuación representa una circunferencia real con radio \( r = \displaystyle \frac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
- Si \( D^2 + E^2 - 4F = 0 \): la ecuación representa una circunferencia degenerada (un punto)
- Si \( D^2 + E^2 - 4F < 0 \): la ecuación no tiene soluciones reales (circunferencia imaginaria)
Posición de un Punto respecto a la Circunferencia
Dada una circunferencia de ecuación \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) y un punto \( P(x_P, y_P) \), podemos determinar la posición relativa del punto respecto a la circunferencia calculando la cantidad:
\[ \delta = (x_P - x_0)^2 + (y_P - y_0)^2 - r^2 \]
Se tienen tres posibilidades:
- Si \( \delta = 0 \): el punto pertenece a la circunferencia
- Si \( \delta < 0 \): el punto es interior a la circunferencia
- Si \( \delta > 0 \): el punto es exterior a la circunferencia
Equivalentemente, comparando la distancia \( d = \sqrt{(x_P - x_0)^2 + (y_P - y_0)^2} \) del punto al centro con el radio:
- Si \( d = r \): punto sobre la circunferencia
- Si \( d < r \): punto interior
- Si \( d > r \): punto exterior
Recta Tangente a la Circunferencia
Dada una circunferencia de centro \( C(x_0, y_0) \) y radio \( r \), y un punto \( P(x_1, y_1) \) perteneciente a la circunferencia, la ecuación de la recta tangente a la circunferencia en el punto \( P \) es:
\[ (x_1 - x_0)(x - x_0) + (y_1 - y_0)(y - y_0) = r^2 \]
En el caso particular de circunferencia centrada en el origen \( x^2 + y^2 = r^2 \), la ecuación de la tangente en el punto \( P(x_1, y_1) \) se simplifica en:
\[ x_1 x + y_1 y = r^2 \]
La recta tangente es perpendicular al radio trazado en el punto de tangencia. Este resultado deriva del hecho de que el vector \( \overrightarrow{CP} = (x_1 - x_0, y_1 - y_0) \) es normal a la tangente.
Tangentes desde un Punto Exterior
Desde un punto exterior \( P(x_P, y_P) \) a una circunferencia se pueden trazar exactamente dos rectas tangentes. Los puntos de tangencia se obtienen resolviendo el sistema formado por la ecuación de la circunferencia y la condición de que la distancia del centro a la recta sea igual al radio.
Intersección de Dos Circunferencias
Dadas dos circunferencias:
\[ \Gamma_1: \quad x^2 + y^2 + D_1 x + E_1 y + F_1 = 0 \] \[ \Gamma_2: \quad x^2 + y^2 + D_2 x + E_2 y + F_2 = 0 \]
Para encontrar los puntos de intersección, resolvemos el sistema formado por las dos ecuaciones. Restando la segunda de la primera, obtenemos la ecuación del eje radical:
\[ (D_1 - D_2)x + (E_1 - E_2)y + (F_1 - F_2) = 0 \]
El eje radical es una recta que, cuando las circunferencias se intersectan, pasa por los dos puntos de intersección. Las posiciones relativas de las circunferencias dependen de la distancia \( d \) entre los centros y de los radios \( r_1, r_2 \):
- Si \( d > r_1 + r_2 \): circunferencias externas (ninguna intersección)
- Si \( d = r_1 + r_2 \): circunferencias tangentes externamente (un punto de intersección)
- Si \( |r_1 - r_2| < d < r_1 + r_2 \): circunferencias secantes (dos puntos de intersección)
- Si \( d = |r_1 - r_2| \): circunferencias tangentes internamente (un punto de intersección)
- Si \( d < |r_1 - r_2| \): una circunferencia interna a la otra (ninguna intersección)
Haz de Circunferencias
Un haz de circunferencias es un conjunto de circunferencias dependientes de un parámetro. El haz generado por dos circunferencias \( \Gamma_1 \) y \( \Gamma_2 \) tiene ecuación:
\[ \lambda \Gamma_1 + \mu \Gamma_2 = 0 \]
donde \( \lambda \) y \( \mu \) son parámetros reales no ambos nulos. Explícitamente:
\[ \lambda(x^2 + y^2 + D_1 x + E_1 y + F_1) + \mu(x^2 + y^2 + D_2 x + E_2 y + F_2) = 0 \]
Se distinguen diversos tipos de haces:
- Haz elíptico: las circunferencias base no se intersectan; todas las circunferencias del haz son reales
- Haz parabólico: las circunferencias base son tangentes; el haz contiene rectas (circunferencias degeneradas)
- Haz hiperbólico: las circunferencias base se intersectan en dos puntos; el haz contiene circunferencias reales e imaginarias
Simetrías y Propiedades Geométricas
La circunferencia posee notables propiedades de simetría que la convierten en una figura geométrica de particular interés:
Simetrías
- Simetría central: toda circunferencia es simétrica respecto a su propio centro
- Ejes de simetría: toda recta que pasa por el centro es un eje de simetría
- Invariancia por rotación: la circunferencia es invariante para cualquier rotación alrededor del centro
Propiedades Métricas
- Longitud (circunferencia): \( C = 2\pi r \)
- Área del círculo: \( A = \pi r^2 \)
- Ángulo central e inscrito: un ángulo inscrito es la mitad del correspondiente ángulo central
Ejercicios Resueltos
Ejercicio 1. Verificar si el punto \( P(3, 4) \) pertenece a la circunferencia de ecuación \( x^2 + y^2 = 25 \).
Solución. Sustituimos las coordenadas del punto en la ecuación:
\[ 3^2 + 4^2 = 9 + 16 = 25 \]
Puesto que la igualdad se verifica, el punto \( P(3, 4) \) pertenece a la circunferencia. Geométricamente, esto significa que la distancia de \( P \) al origen es exactamente igual al radio \( r = 5 \).
Ejercicio 2. Determinar la ecuación de la circunferencia con centro \( C(2, -3) \) y radio \( r = 4 \).
Solución. Aplicando la forma canónica:
\[ (x - 2)^2 + (y - (-3))^2 = 4^2 \] \[ (x - 2)^2 + (y + 3)^2 = 16 \]
Desarrollando, obtenemos la forma general:
\[ x^2 - 4x + 4 + y^2 + 6y + 9 = 16 \] \[ x^2 + y^2 - 4x + 6y - 3 = 0 \]
Ejercicio 3. Dada la ecuación \( x^2 + y^2 + 6x - 8y + 5 = 0 \), determinar centro y radio de la circunferencia.
Solución. Completamos los cuadrados:
\[ x^2 + 6x = (x + 3)^2 - 9 \] \[ y^2 - 8y = (y - 4)^2 - 16 \]
Sustituyendo:
\[ (x + 3)^2 - 9 + (y - 4)^2 - 16 + 5 = 0 \] \[ (x + 3)^2 + (y - 4)^2 = 20 \]
Por tanto:
- Centro: \( C(-3, 4) \)
- Radio: \( r = \sqrt{20} = 2\sqrt{5} \)
Ejercicio 4. Encontrar la ecuación de la circunferencia que pasa por los puntos \( A(1, 0) \), \( B(0, 1) \) y \( C(-1, 0) \).
Solución. Utilizamos la forma general \( x^2 + y^2 + Dx + Ey + F = 0 \) e imponemos el paso por los tres puntos:
Para \( A(1, 0) \):
\[ 1 + 0 + D + 0 + F = 0 \implies D + F = -1 \]
Para \( B(0, 1) \):
\[ 0 + 1 + 0 + E + F = 0 \implies E + F = -1 \]
Para \( C(-1, 0) \):
\[ 1 + 0 - D + 0 + F = 0 \implies -D + F = -1 \]
Resolviendo el sistema:
\[ \begin{cases} D + F = -1 \\ E + F = -1 \\ -D + F = -1 \end{cases} \]
De la primera y tercera ecuación: \( D = 0 \), por tanto \( F = -1 \). De la segunda ecuación: \( E = 0 \).
La ecuación buscada es: \( x^2 + y^2 - 1 = 0 \), o sea \( x^2 + y^2 = 1 \).
Esta es la circunferencia unitaria centrada en el origen.
Ejercicio 5. Determinar las tangentes a la circunferencia \( x^2 + y^2 = 9 \) trazadas desde el punto exterior \( P(5, 0) \).
Solución. Sea \( T(x_T, y_T) \) un punto de tangencia. La recta \( PT \) tiene ecuación de la tangente en el punto \( T \):
\[ x_T x + y_T y = 9 \]
Puesto que esta recta pasa por \( P(5, 0) \):
\[ 5x_T + 0 \cdot y_T = 9 \Rightarrow x_T = \frac{9}{5} \]
Siendo \( T \) sobre la circunferencia: \( x_T^2 + y_T^2 = 9 \), por tanto:
\[ \left(\frac{9}{5}\right)^2 + y_T^2 = 9 \Rightarrow y_T^2 = 9 - \frac{81}{25} = \frac{144}{25} \Rightarrow y_T = \pm\frac{12}{5} \]
Los puntos de tangencia son:
\[ T_1\left(\frac{9}{5}, \frac{12}{5}\right) \quad \text{y} \quad T_2\left(\frac{9}{5}, -\frac{12}{5}\right) \]
Las ecuaciones de las tangentes son:
\[ \frac{9}{5}x + \frac{12}{5}y = 9 \quad \implies \quad 3x + 4y = 15 \] \[ \frac{9}{5}x - \frac{12}{5}y = 9 \quad \implies \quad 3x - 4y = 15 \]

