El Teorema de Rolle es un resultado fundamental aplicable a las funciones continuas y derivables. Este teorema establece que, si una función \( f \) es continua en un intervalo cerrado \([a,b]\), derivable en el intervalo abierto \((a,b)\) y toma el mismo valor en los extremos \( f(a) = f(b) \), entonces existe al menos un punto interno \( \xi \in (a,b) \) en el que la derivada de la función se anula, es decir, \( f'(\xi) = 0 \). Este resultado tiene numerosas aplicaciones, incluida la demostración del Teorema del Valor Medio.
Índice
Teorema de Rolle
Sea \( f : [a,b] \to \mathbb{R} \) una función continua en el intervalo cerrado \([a,b]\), derivable en el intervalo abierto \((a,b)\) y tal que \( f(a) = f(b) \). Entonces, existe al menos un punto \( \xi \in (a,b) \) tal que: \[ f'(\xi) = 0 \]
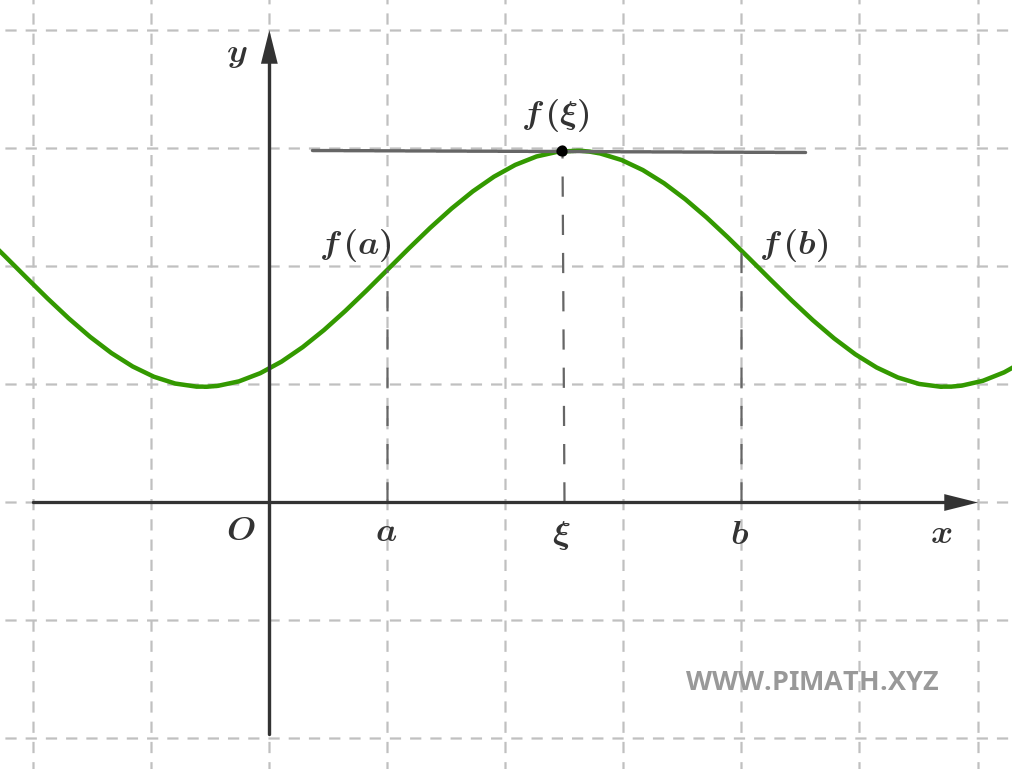
Demostración. En primer lugar, dado que \( f \) es continua en \([a,b]\), por el Teorema de Weierstrass admite máximo y mínimo absolutos en el intervalo. Por lo tanto, existen puntos \( c, d \in [a,b] \) tales que: \[ f(c) = M \quad \text{y} \quad f(d) = m \] donde \( M = \max_{x \in [a,b]} f(x) \) y \( m = \min_{x \in [a,b]} f(x) \).
Consideremos primero el caso en que la función \( f \) sea constante, es decir, \( f(x) = k \) para todo \( x \in [a,b] \). En tal caso, por definición de derivada: \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{k - k}{h} = 0 \] para todo \( x \in (a,b) \). La tesis queda entonces inmediatamente verificada.
Pasemos ahora al caso en que \( f \) no sea constante. Como \( f(a) = f(b) \), el máximo y el mínimo absolutos no pueden encontrarse ambos en los extremos \( a \) y \( b \). Debe existir al menos un punto \( \xi \in (a,b) \) donde \( f(\xi) = M \) o \( f(\xi) = m \). En ambos casos, \( \xi \) representa un punto de máximo o mínimo local.
Sea \( \xi \) un punto de máximo local. Para \( h \) suficientemente pequeño:
\[ f(\xi + h) \leq f(\xi) \]
Podemos entonces considerar los cocientes incrementales:
\[ \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \quad \text{si} \ h > 0 \]
\[ \frac{f(\xi + h) - f(\xi)}{h} \geq 0 \quad \text{si} \ h < 0 \]
Dado que \( f \) es derivable en \( \xi \), existe el límite del cociente incremental, es decir: \[ f'(\xi) = \lim_{h \to 0} \frac{f(\xi + h) - f(\xi)}{h} \]
De lo dicho anteriormente, tenemos:
\[ \lim_{h \to 0^+} \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \leq \lim_{h \to 0^-} \frac{f(\xi + h) - f(\xi)}{h} \]
Por lo tanto, necesariamente: \[ f'(\xi) = 0 \]
Un razonamiento análogo se aplica en el caso en que \( \xi \) sea un punto de mínimo local.
Así hemos demostrado que existe al menos un punto \( \xi \in (a,b) \) tal que \( f'(\xi) = 0 \), completando la demostración del Teorema de Rolle.