Una ecuación es de segundo grado si y solo si puede escribirse en la siguiente forma:
\[ a x ^ 2 + b x + c = 0 \quad , \quad a \neq 0 \]
denominada forma canónica. Los números reales \( a , b \) y \( c \) reciben el nombre de coeficiente cuadrático, lineal y término independiente.
Siempre se puede suponer que el coeficiente cuadrático es mayor que cero. En efecto, en el caso de que \( a < 0 \), basta multiplicar ambos miembros por \( -1 \) para reducirse al caso \( a > 0 \).
Índice
- Completar el Cuadrado
- Fórmula Reducida
- Ecuaciones de Segundo Grado Monomias
- Ecuaciones de Segundo Grado Puras
- Ecuaciones de Segundo Grado Incompletas
- Relación entre Suma y Producto de las Raíces
- Ejercicios Resueltos
- Significado Geométrico
Completar el Cuadrado
En esta sección deduciremos la fórmula general para resolver cualquier ecuación de segundo grado. Partimos de la forma canónica:
\[ ax^2 + bx + c = 0, \quad a \neq 0 \]
Para simplificar los cálculos, dividimos todo entre \( a \), de modo que el coeficiente del término cuadrático sea igual a 1:
\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]
Ahora, aislamos el término independiente llevándolo al segundo miembro:
\[ x^2 + \frac{b}{a}x = -\frac{c}{a} \]
En este punto, aplicamos el método de completar el cuadrado. El truco consiste en agregar y sustraer una cantidad para transformar el primer miembro en un cuadrado perfecto. En este caso, el término que falta es
\[ \left(\frac{b}{2a}\right)^2 \]
Lo agregamos a ambos miembros:
\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 \]
El primer miembro ahora es el cuadrado de un binomio, por tanto podemos escribirlo como
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2} \]
Reescribimos el segundo miembro con denominador común:
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} \]
Ahora podemos extraer la raíz cuadrada de ambos miembros, recordando que \( \sqrt{x^2} = |x| \):
\[ \left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a} \]
De aquí obtenemos directamente \( x \):
\[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
Finalmente, despejamos \( x \) y obtenemos la célebre fórmula general:
\[ x_{1,2} = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
El término bajo la raíz, conocido como discriminante y denotado con \( \Delta \), se define como:
\[ \Delta = b^2 - 4ac \]
¿Pero qué representa el discriminante? Nos permite determinar de un vistazo el tipo de soluciones que tendrá la ecuación. Analicémoslo en los tres casos posibles:
- \( \Delta > 0 \): el discriminante es positivo, por lo que la raíz es un número real. Esto significa que la ecuación tiene dos soluciones reales y distintas.
- \( \Delta = 0 \): la raíz cuadrada de cero es cero, por lo que la fórmula nos da una única solución repetida. En otras palabras, la ecuación tiene dos soluciones coincidentes (o una solución doble).
- \( \Delta < 0 \): la raíz de un número negativo no es un número real, por lo que la ecuación no tiene soluciones reales, sino dos soluciones complejas con parte imaginaria.
Esto significa que, observando solo el valor de \( \Delta \), podemos predecir la naturaleza de las soluciones sin necesidad de resolver directamente la ecuación.
Fórmula Reducida
La fórmula reducida es una versión simplificada de la fórmula general de las ecuaciones de segundo grado, útil cuando el coeficiente \( b \) es par.
Consideremos una ecuación de segundo grado en la forma canónica:
\[ ax^2 + bx + c = 0 \]
Si el coeficiente \( b \) es par, podemos escribirlo como:
\[ b = 2k \]
Sustituyendo en la ecuación obtenemos:
\[ ax^2 + 2kx + c = 0 \]
La fórmula general clásica es:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Sustituyendo \( b = 2k \):
\[ x = \frac{-2k \pm \sqrt{(2k)^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm \sqrt{4k^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm 2\sqrt{k^2 - ac}}{2a} \]
Dividiendo numerador y denominador entre 2:
\[ x = \frac{-k \pm \sqrt{k^2 - ac}}{a} \]
Finalmente, podemos expresar la fórmula reducida como:
\[ x = \frac{-\frac{b}{2} \pm \sqrt{\left(\frac{b}{2}\right)^2 - ac}}{a} \]
El discriminante reducido está dado por:
\[ \Delta' = \left(\frac{b}{2}\right)^2 - ac \]
Ahora comparémoslo con el discriminante de la fórmula completa:
\[ \Delta = b^2 - 4ac \]
Sustituyendo \( b = 2k \), obtenemos:
\[ \Delta = (2k)^2 - 4ac \]
\[ \Delta = 4k^2 - 4ac \]
Dividiendo todo entre 4:
\[ \frac{\Delta}{4} = k^2 - ac \]
Puesto que \( k = \displaystyle \frac{b}{2} \), podemos reescribir:
\[ \frac{\Delta}{4} = \left(\frac{b}{2}\right)^2 - ac \]
que es exactamente la definición de \( \Delta' \).
Por tanto, podemos concluir que:
\[ \Delta' = \frac{\Delta}{4} \]
Ecuaciones de Segundo Grado Monomias
Una ecuación se dice monomia si se reduce a un único término cuadrático, es decir, de la forma:
\[ ax^2 = 0 \]
Para resolver esta ecuación, dividimos ambos miembros entre \( a \) (suponiendo \( a \neq 0 \)):
\[ x^2 = 0 \]
Extrayendo la raíz cuadrada, obtenemos la solución:
\[ x = 0 \]
Aunque el valor es único, matemáticamente se consideran dos soluciones coincidentes: \( x_1 = x_2 = 0 \).
Ecuaciones de Segundo Grado Puras
Una ecuación se dice pura si, en la forma general \( ax^2 + bx + c = 0 \), el coeficiente \( b \) es nulo, reduciéndose a:
\[ ax^2 + c = 0 \]
Para resolver esta ecuación, llevamos el término independiente \( c \) al segundo miembro:
\[ ax^2 = -c \]
Dividimos ambos miembros entre \( a \neq 0 \):
\[ x^2 = -\frac{c}{a} \]
Las soluciones existen solo si \( \displaystyle -\frac{c}{a} \geq 0 \), de lo contrario la ecuación no tiene soluciones reales. Si el valor bajo la raíz es positivo, obtenemos:
\[ x_{1,2} = \pm \sqrt{-\frac{c}{a}} \]
Ecuaciones de Segundo Grado Incompletas
Una ecuación se dice incompleta si el término independiente es nulo, es decir:
\[ ax^2 + bx = 0 \]
En este caso, podemos resolverla factorizando \( x \) como factor común:
\[ x (ax + b) = 0 \]
Aplicando la ley de anulación del producto, obtenemos las dos soluciones:
\[ x = 0 \quad \text{o bien} \quad x = -\frac{b}{a} \]
Relación entre Suma y Producto de las Raíces
Consideremos la ecuación cuadrática del tipo \( ax^2 + bx + c = 0 \), donde \( a \), \( b \) y \( c \) son los coeficientes. Sean \( x_1 \) y \( x_2 \) las raíces de esta ecuación. Ahora, queremos escribir la ecuación en términos de las raíces. Una ecuación de segundo grado puede escribirse como el producto de los factores \( (x - x_1) \) y \( (x - x_2) \), por tanto podemos escribir:
\[ a(x - x_1)(x - x_2) = 0 \]
Desarrollando el producto de la izquierda, obtenemos:
\[ a(x^2 - (x_1 + x_2)x + x_1x_2) = 0 \]
Ahora, por la propiedad distributiva, obtenemos:
\[ ax^2 - a(x_1 + x_2)x + ax_1x_2 = 0 \]
En este punto, podemos comparar esta expresión con la ecuación canónica \( ax^2 + bx + c = 0 \). En particular, vemos que los coeficientes deben ser iguales. Comparando el término lineal, obtenemos:
\[ -a(x_1 + x_2) = b \]
Despejando \( x_1 + x_2 \), obtenemos:
\[ x_1 + x_2 = -\frac{b}{a} \]
De la misma manera, comparando el término constante, obtenemos:
\[ ax_1x_2 = c \]
Despejando el producto de las raíces, obtenemos:
\[ x_1 \cdot x_2 = \frac{c}{a} \]
En síntesis, las raíces \( x_1 \) y \( x_2 \) están relacionadas con los coeficientes \( a \), \( b \) y \( c \) a través de estas dos sencillas relaciones: la suma de las raíces es \( \displaystyle -\frac{b}{a} \) y el producto de las raíces es \( \displaystyle \frac{c}{a} \). Estas propiedades son fundamentales y nos permiten deducir información importante sobre las raíces sin calcularlas directamente.
Ejercicios Resueltos
Ejercicio 1. Resolver la ecuación de segundo grado \( x^2 - 3x - 5 = 0 \).
Solución. Para resolverla, utilizamos la siguiente fórmula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
En este caso, los coeficientes son \( a = 1 \), \( b = -3 \) y \( c = -5 \). Aplicando la fórmula:
\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-5)}}{2(1)} = \frac{3 \pm \sqrt{9 + 20}}{2} = \frac{3 \pm \sqrt{29}}{2} \]
Las soluciones son por tanto:
\[ x_1 = \frac{3 + \sqrt{29}}{2} \quad , \quad x_2 = \frac{3 - \sqrt{29}}{2} \]
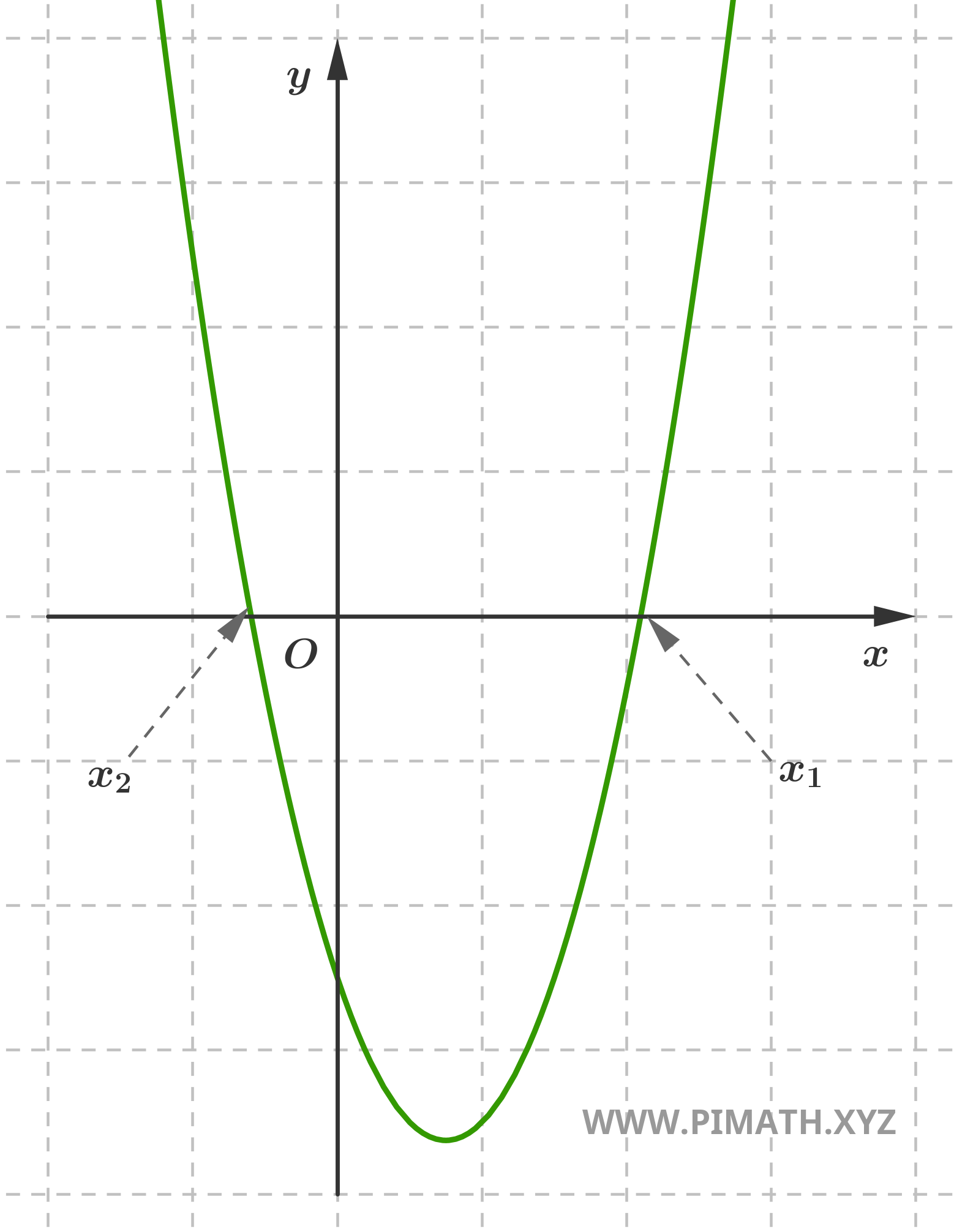
Ejercicio 2 (forma reducida). Encontrar las soluciones de la siguiente ecuación \( x^2 + 6x = 0 \).
Solución. Para resolverla, podemos factorizar el factor común:
\[ x(x + 6) = 0 \]
Las soluciones son por tanto: \( x_1 = 0 \) y \( x_2 = -6 \).
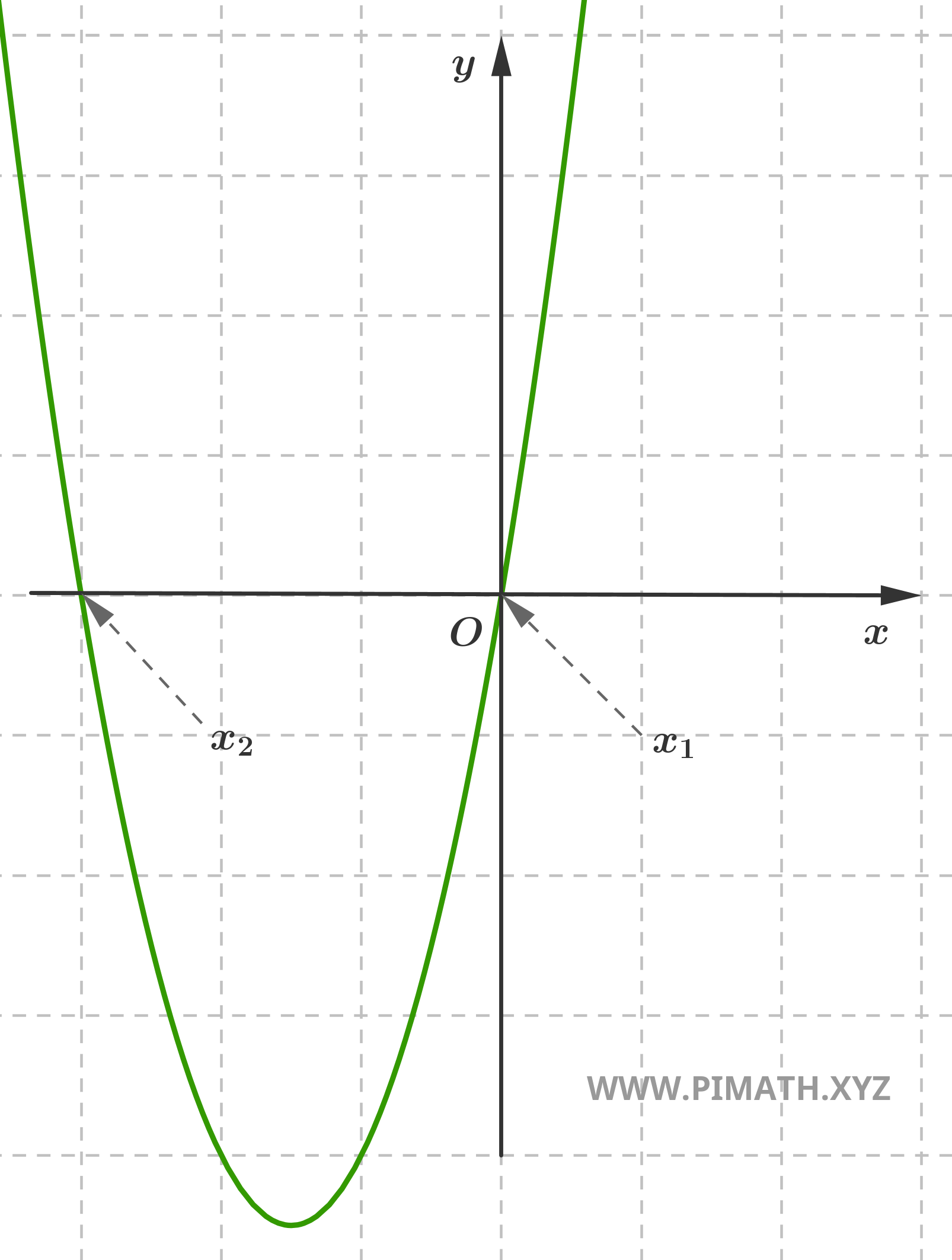
Ejercicio 3 (ecuación pura). Encontrar las soluciones de la ecuación \( x^2 = 16 \).
Solución. Para resolverla, podemos extraer la raíz cuadrada de ambos miembros:
\[ x = \pm \sqrt{16} = \pm 4 \]
Las soluciones son por tanto: \( x_1 = 4 \) y \( x_2 = -4 \).
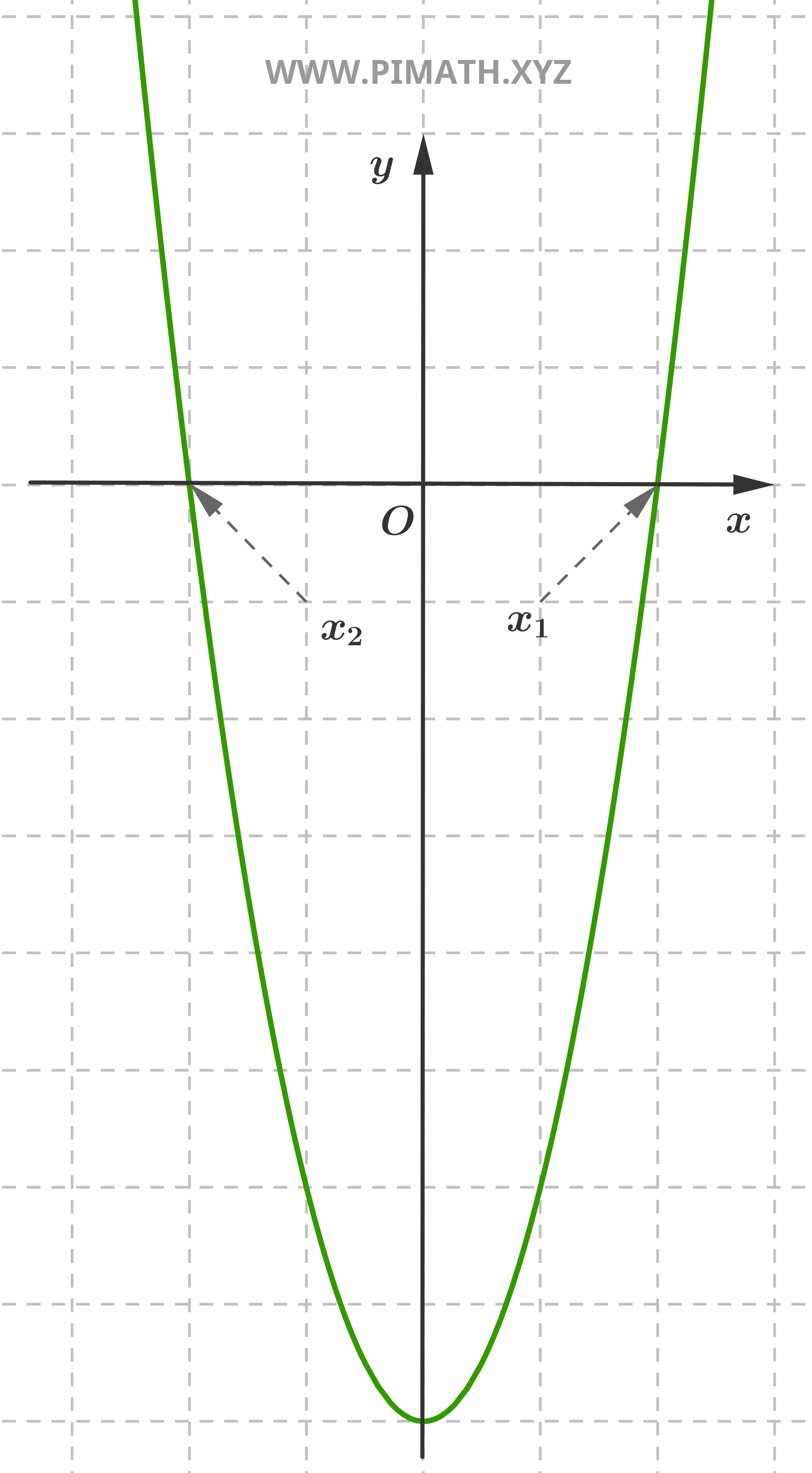
Ejercicio 4 (ecuación pura). Encontrar las soluciones de la ecuación \( x^2 + 9 = 0 \).
Solución. Aislamos \( x^2 \):
\[ x^2 = -9 \]
Puesto que no existen números reales que satisfagan esta ecuación, la ecuación no admite soluciones reales.
Ejercicio 5. Encontrar las soluciones de la siguiente ecuación \( x^2 - 4 = 0 \).
Solución. Aislamos \( x^2 \):
\[ x^2 = 4 \]
Ahora extraemos la raíz cuadrada de ambos miembros:
\[ x = \pm \sqrt{4} = \pm 2 \]
Las soluciones son por tanto:
\[ x_1 = 2 \quad , \quad x_2 = -2 \]
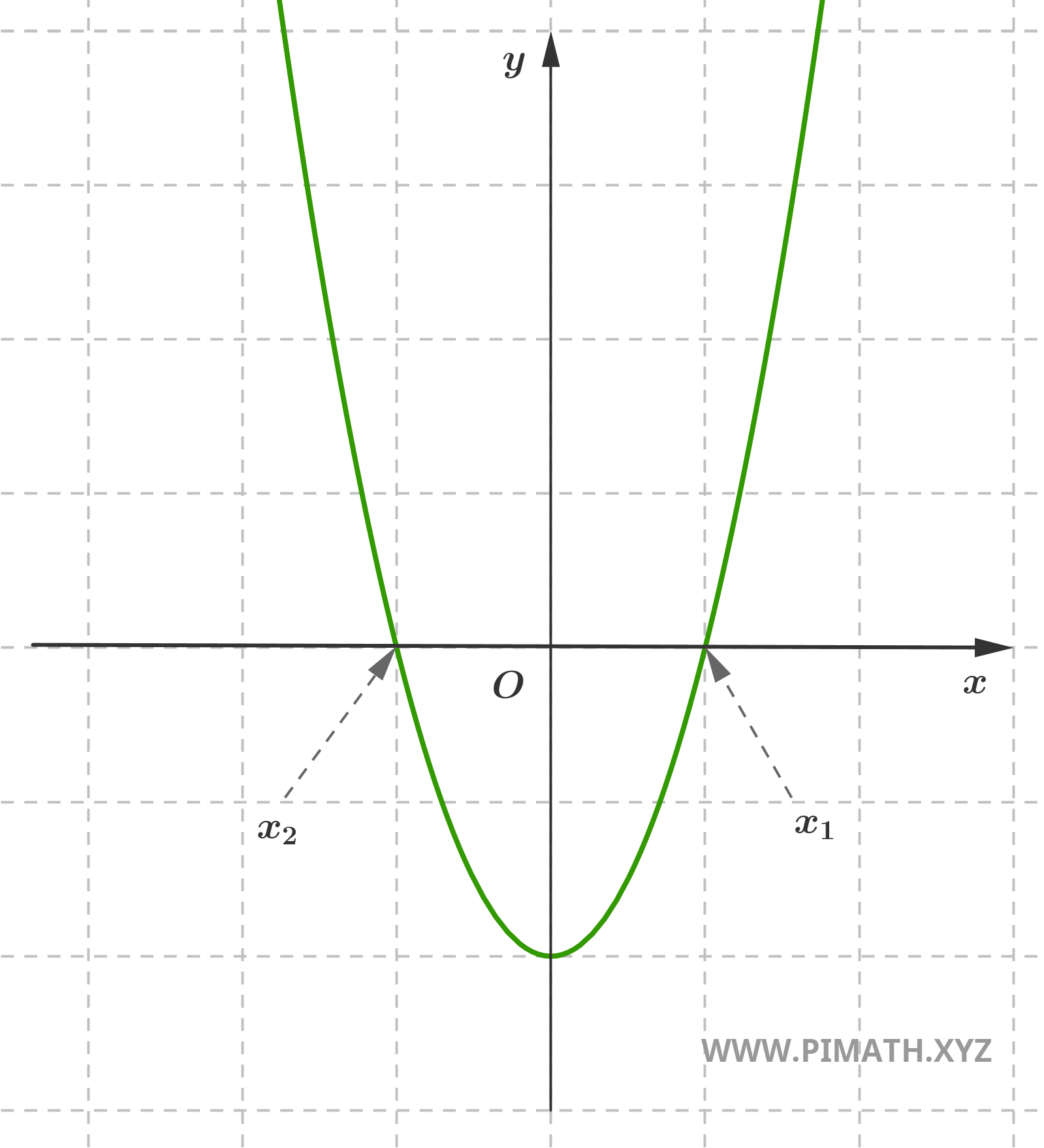
Significado Geométrico
Desde el punto de vista geométrico, resolver una ecuación de segundo grado significa encontrar los valores reales (si existen) para los cuales la parábola de ecuación \( y = ax^2 + bx + c \) interseca el eje de las abscisas \( x \) o, si se prefiere, la recta \( y = 0 \).

