L'ellipse est le lieu géométrique des points du plan pour lesquels la somme des distances à deux points fixes, appelés foyers, est constante. Elle possède deux axes de symétrie, appelés grand axe et petit axe. C'est une courbe fermée et symétrique, avec de nombreuses applications en physique et en géométrie.
Sommaire
- Comment déterminer l'équation canonique de l'ellipse
- Ellipse à demi-grand axe sur l'axe des ordonnées
- Comment déterminer l'équation de l'ellipse translatée
- Relations entre les paramètres de l'ellipse
- Excentricité de l'ellipse : définition, signification géométrique et formule
- Exercices résolus
Notons les deux foyers \( F_1(-c, 0) \) et \( F_2(c, 0) \), et soit \( P(x, y) \) un point quelconque appartenant à l'ellipse. On a alors la relation suivante :
\[ |PF_1| + |PF_2| = 2a \]
La constante \( 2a \) – qui représente la somme des distances \( |PF_1|\) et \(|PF_2|\) – est toujours supérieure à la distance entre les deux foyers, \( 2c \). Ce concept est illustré dans la figure suivante :
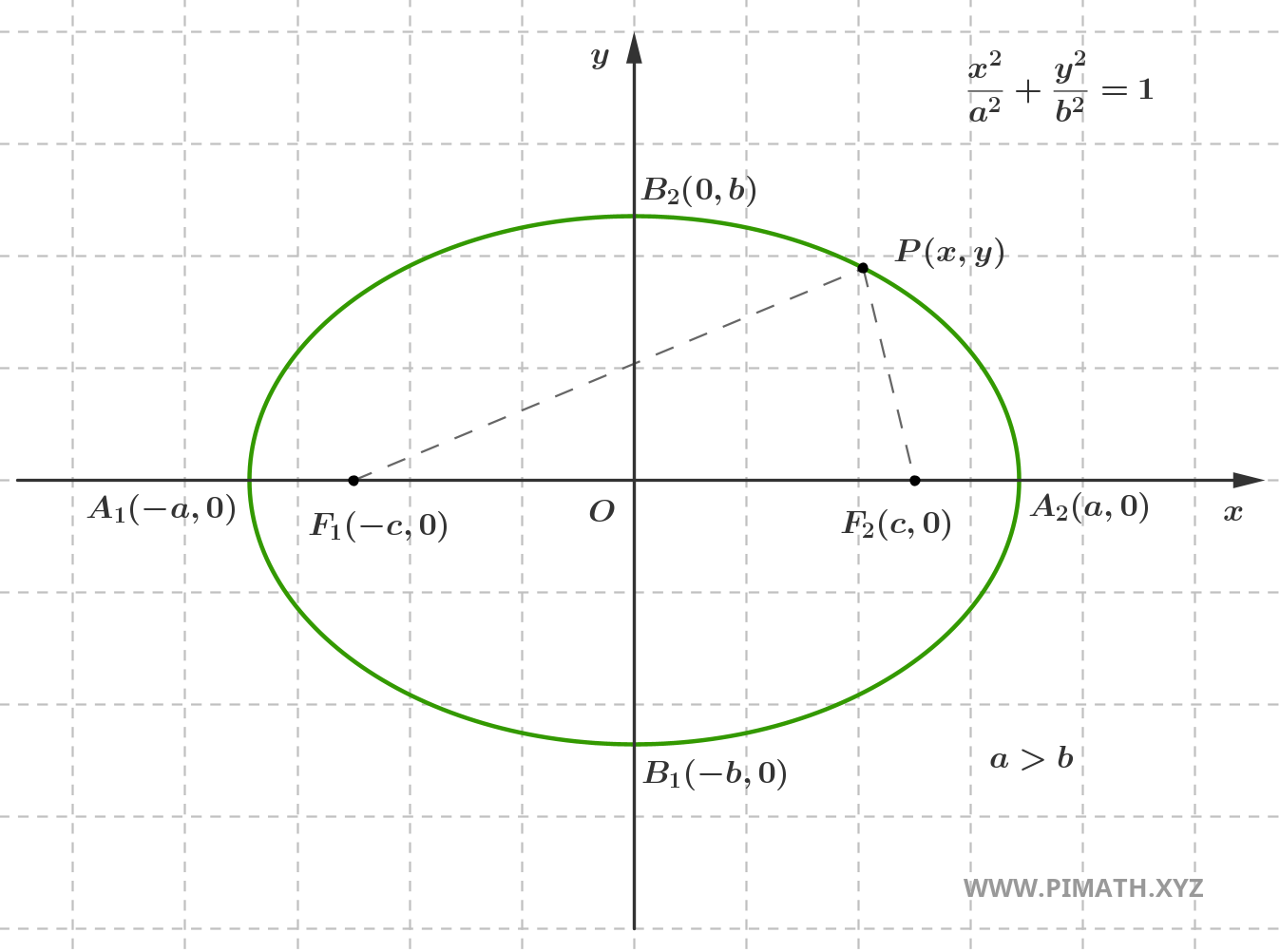
Dans l'image, le segment qui relie le centre \( O \) au point \( A_2 \) sur l'axe horizontal est appelé demi-grand axe, et sa longueur est exactement \( a \). Le segment vertical qui relie le centre au point \( B_2 \) est appelé demi-petit axe et a pour longueur \( b \).
La relation qui définit l'ellipse doit naturellement être vérifiée pour tous les points de l'ellipse. Plaçons-nous dans le cas particulier où le point \( P(x,y) \) coïncide avec le point \( B_2(0,b) \) :
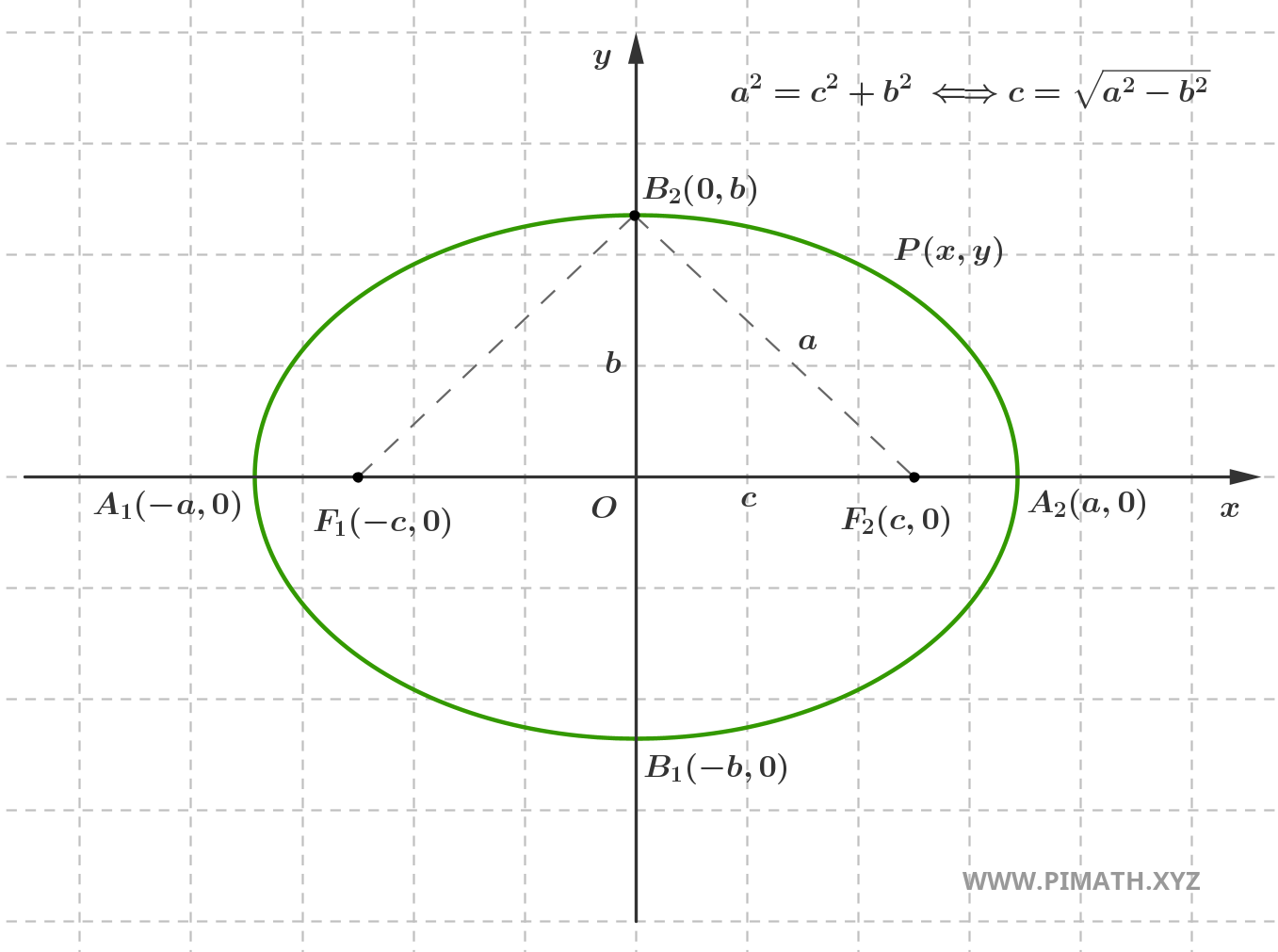
En considérant le triangle rectangle ayant pour sommets \( O(0,0) \), \( F_2(c,0) \) et \( B_2(0,b) \) et en appliquant le théorème de Pythagore, on obtient \( c=\sqrt{a^2-b^2} \), comme le montre la figure.
Comment déterminer l'équation canonique de l'ellipse
Considérons un cas simplifié où le centre de l'ellipse coïncide avec l'origine du repère, avec les foyers positionnés le long de l'axe horizontal aux points \( F_1(-c, 0) \) et \( F_2(c, 0) \).
Considérons un point quelconque \( P(x, y) \) du plan. Pour que \( P \) appartienne à l'ellipse, la relation suivante doit être vérifiée :
\[ |PF_1| + |PF_2| = 2a \quad , \quad a > c \]
Calculons maintenant les distances entre le point \( P(x, y) \) et chacun des deux foyers :
\[ |PF_1| = \sqrt{(x + c)^2 + y^2} \quad \text{et} \quad |PF_2| = \sqrt{(x - c)^2 + y^2} \]
En substituant ces expressions dans la condition initiale, nous obtenons :
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \]
Pour éliminer l'un des radicaux, nous faisons passer \( \sqrt{(x + c)^2 + y^2} \) dans le membre de droite :
\[ \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2} \]
Nous élevons au carré les deux membres pour éliminer le radical :
\[ (x - c)^2 + y^2 = \left(2a - \sqrt{(x + c)^2 + y^2} \right)^2 \]
Nous développons le carré du membre de droite :
\[ (x - c)^2 + y^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
Nous éliminons le terme \( y^2 \) présent des deux côtés et développons les carrés :
\[ x^2 - 2cx + c^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 \]
En simplifiant les deux membres :
\[ -4cx = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} \]
Nous divisons les deux membres par 4 :
\[ -cx = a^2 - a\sqrt{(x + c)^2 + y^2} \]
Nous faisons passer tous les termes contenant le radical dans le membre de gauche :
\[ a\sqrt{(x + c)^2 + y^2} = a^2 + cx \]
Nous élevons de nouveau au carré les deux membres :
\[ a^2[(x + c)^2 + y^2] = (a^2 + cx)^2 \]
Nous développons les deux membres :
\[ a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2 \]
Nous développons complètement :
\[ a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2 \]
Nous simplifions les termes communs des deux côtés :
\[ a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2 \]
Nous regroupons les termes semblables :
\[ x^2(a^2 - c^2) + a^2y^2 = a^2(a^2 - c^2) \]
Puisque \( a > c \), la quantité \( a^2 - c^2 \) est positive. Notons-la \( b^2 \), nous obtenons ainsi :
\[ b^2 = a^2 - c^2 \]
En substituant, nous obtenons :
\[ x^2b^2 + a^2y^2 = a^2b^2 \]
Nous divisons les deux membres par \( a^2b^2 \) pour isoler les termes :
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , \quad a > b \]
Voici la forme canonique de l'équation de l'ellipse centrée à l'origine avec les foyers sur l'axe des abscisses. L'équation est symétrique par rapport aux deux axes de coordonnées et par rapport à l'origine.
Introduisons quelques éléments de nomenclature. La droite qui contient les foyers s'appelle l'axe focal, tandis que le point d'intersection des axes est le centre de l'ellipse.
- Les points où l'ellipse coupe l'axe focal et la droite perpendiculaire à celui-ci passant par le centre sont appelés sommets de l'ellipse.
- Le segment \( A_1A_2 \) est appelé grand axe, tandis que le segment \( B_1B_2 \) est appelé petit axe.
- On définit demi-grand axe la longueur \( a \), et demi-petit axe la longueur \( b \).
Ellipse à demi-grand axe sur l'axe des ordonnées
Si nous voulons décrire une ellipse qui a le demi-grand axe vertical, c'est-à-dire orienté le long de l'axe des ordonnées, nous devons simplement échanger les rôles de \( a \) et \( b \) dans l'équation canonique qui décrit l'ellipse à demi-grand axe sur l'axe des abscisses, comme le montre la figure :
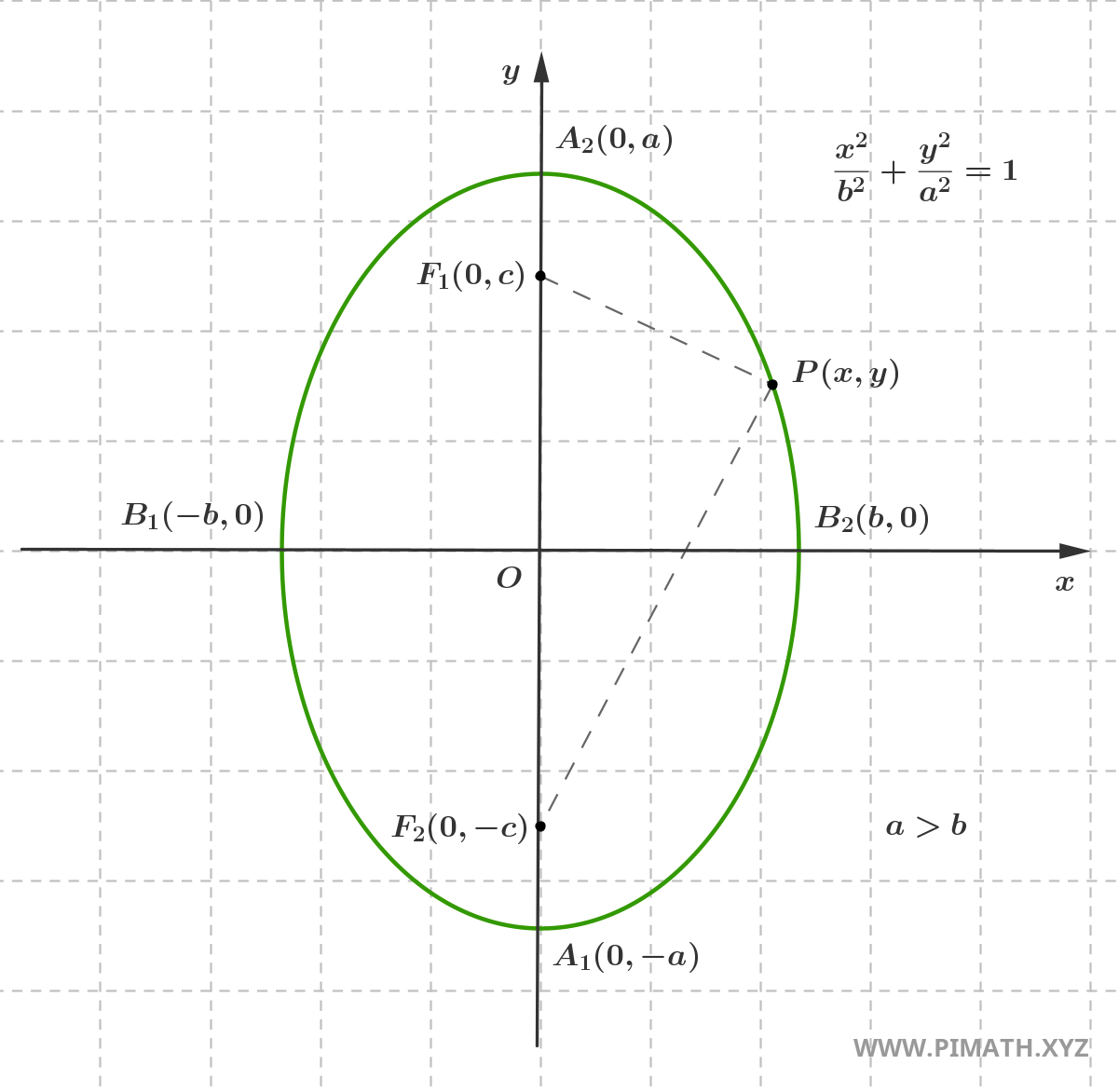
Dans ce cas, en imposant \( |PF_1| + |PF_2| = 2a \) et avec des étapes algébriques analogues, l'équation de l'ellipse devient :
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \]
Ce changement reflète une rotation de l'ellipse de 90 degrés par rapport à l'axe des x. La forme de l'équation reste la même, mais l'axe le long duquel l'ellipse se développe change.
Dans ce cas également, le centre de l'ellipse reste à l'origine et la définition géométrique reste valide : pour chaque point \( P(x, y) \) sur l'ellipse, la somme des distances aux foyers (qui sont maintenant positionnés le long de l'axe des y) est toujours égale à \( 2a \).
Comment déterminer l'équation de l'ellipse translatée
Jusqu'à présent, nous avons considéré une ellipse centrée à l'origine avec les foyers sur l'axe des abscisses. Cependant, une ellipse peut se trouver en n'importe quel point du plan. Dans ce cas, on parle d'ellipse translatée.
Supposons que le centre de l'ellipse soit au point \( C(x_0, y_0) \). L'équation canonique se modifie en conséquence, en translatant les coordonnées.
Pour l'équation de l'ellipse translatée, il est essentiel de distinguer quel est le demi-grand axe et quel est le demi-petit axe. Selon l'orientation de l'ellipse par rapport aux axes de coordonnées, l'équation canonique translatée prend des formes légèrement différentes :
Ellipse translatée horizontale
Le grand axe est parallèle à l'axe des x, donc les foyers sont sur la droite \( y = y_0 \)
Dans ce cas, le demi-grand axe \( a \) est la valeur sous le terme \( (x - x_0)^2 \), et le demi-petit axe \( b \) est la valeur sous le terme \( (y - y_0)^2 \).
\[ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 \quad , \quad a > b \]
Ellipse translatée verticale
Le grand axe est parallèle à l'axe des y, donc les foyers sont sur la droite \( x = x_0 \)
Dans ce cas, le demi-grand axe \( a \) est la valeur sous le terme \( (y - y_0)^2 \), et le demi-petit axe \( b \) est la valeur sous le terme \( (x - x_0)^2 \).
\[ \frac{(x - x_0)^2}{b^2} + \frac{(y - y_0)^2}{a^2} = 1 \quad , \quad a > b \]
Remarque : Les foyers ne se trouvent plus sur les axes de coordonnées x ou y, mais sur des droites parallèles à ceux-ci, passant par le centre \( (x_0, y_0) \).
Relations entre les paramètres de l'ellipse
Dans le cas d'une ellipse centrée à l'origine avec les axes parallèles aux axes de coordonnées, la relation entre les paramètres principaux est donnée par une formule fondamentale qui relie le demi-grand axe \( a \), le demi-petit axe \( b \) et la distance des foyers au centre \( c \).
La formule est la suivante :
\[ c^2 = a^2 - b^2 \]
Par conséquent, la distance des foyers au centre peut être calculée comme :
\[ c = \sqrt{a^2 - b^2} \]
Cette relation est valide pour toutes les ellipses centrées à l'origine avec les axes alignés sur les axes de coordonnées, où \( a > b \). Le demi-grand axe est toujours associé à l'axe ayant le plus grand dénominateur dans l'équation canonique de l'ellipse :
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , a > b \quad \text{(si le grand axe est horizontal)} \]
En revanche :
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \quad \text{(si le grand axe est vertical)} \]
Dans ce cas, \( c^2 = a^2 - b^2 \) et donc \( c = \sqrt{a^2 - b^2} \). Connaître ces relations permet de calculer rapidement la position des foyers et de mieux comprendre la géométrie de l'ellipse.
Excentricité de l'ellipse : définition, signification géométrique et formule
L'excentricité est une mesure fondamentale qui nous permet de comprendre à quel point une ellipse s'écarte d'un cercle. Chaque ellipse a deux foyers : ce sont deux points intérieurs tels que la somme des distances de n'importe quel point de l'ellipse aux deux foyers est constante. L'excentricité, notée par la lettre \( e \), est un nombre qui varie de \( 0 \) à \( 1 \) et décrit la forme de l'ellipse.
Définition de l'excentricité
L'excentricité \( e \) n'est pas une donnée que l'on choisit arbitrairement, mais une valeur qui émerge naturellement des propriétés géométriques de l'ellipse. En particulier, si \( a \) est la longueur du demi-grand axe et \( b \) celle du demi-petit axe, alors la distance \( c \) entre le centre et l'un des foyers est : \[c = \sqrt{a^2 - b^2}\] Avec \( a > b \), l'excentricité est toujours donnée par la formule suivante : \[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1-\frac{b^2}{a^2}}\] Cette formule est valide que le grand axe soit horizontal ou vertical, car \( a \) représente toujours le demi-grand axe indépendamment de l'orientation de l'ellipse.
Signification géométrique de l'excentricité
Quand l'excentricité est égale à zéro, c'est-à-dire \( e = 0 \), cela signifie que les deux foyers coïncident au centre de l'ellipse. Dans ce cas, l'ellipse est en réalité un cercle, car tous les rayons (c'est-à-dire les segments qui relient le centre à un point de la courbe) ont la même longueur : \( a = b \).
Quand au contraire l'excentricité est un nombre compris entre \( 0 \) et \( 1 \), c'est-à-dire \( 0 < e < 1 \), l'ellipse est allongée. Plus la valeur de \( e \) est grande, plus les foyers s'éloignent du centre et plus l'ellipse apparaît allongée le long du grand axe et comprimée le long du petit axe.
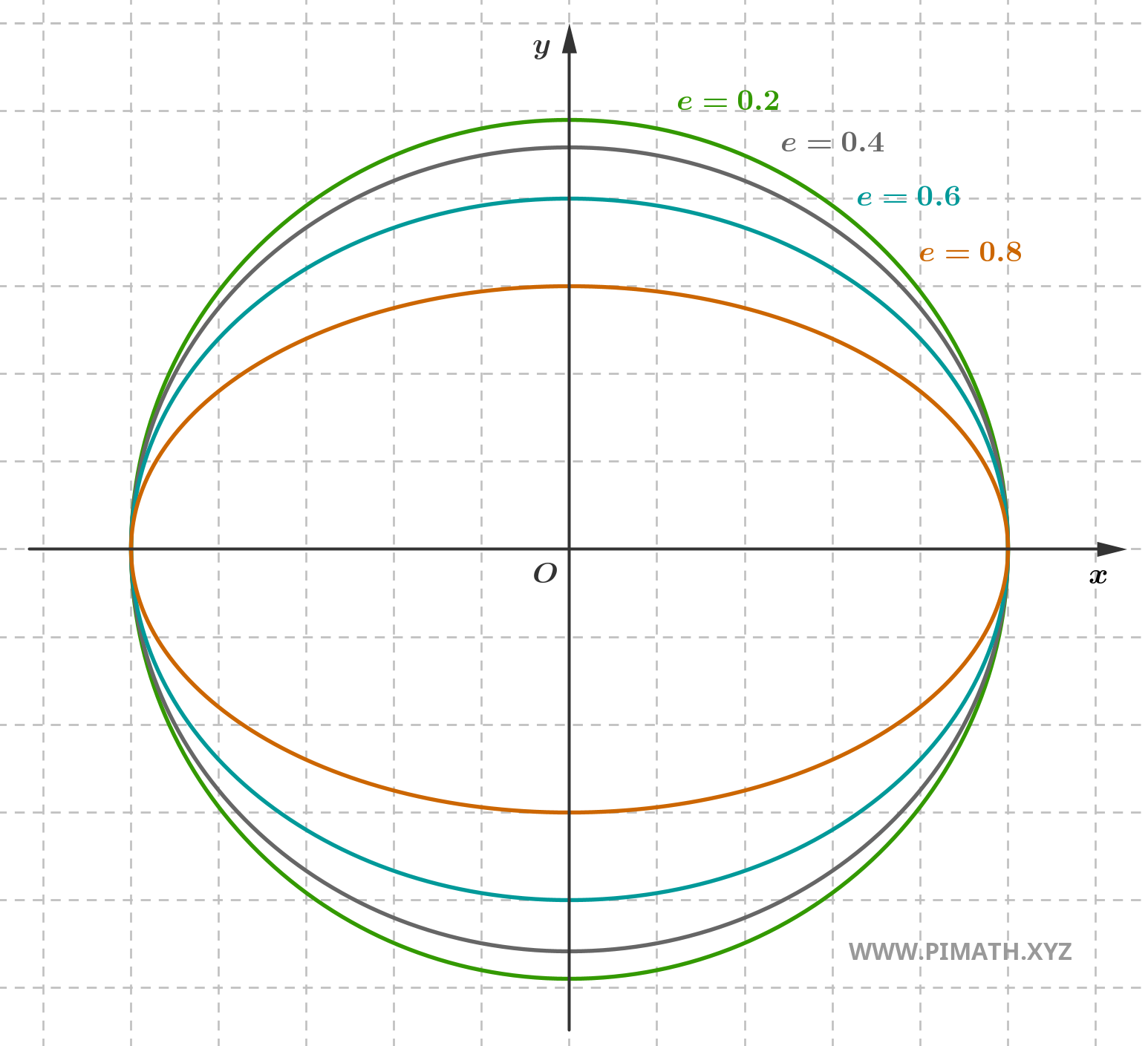
Enfin, quand \( e \) se rapproche de \( 1 \), la forme de l'ellipse devient extrêmement allongée et les foyers sont très éloignés du centre.
Par exemple, considérons une ellipse avec demi-grand axe \( a = 5 \) et demi-petit axe \( b = 3 \).
Calculons d'abord la distance des foyers au centre :
\[c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4\]
À ce stade, nous pouvons calculer l'excentricité :
\[e = \frac{4}{5} = 0{,}8\]
La valeur que nous avons trouvée indique que l'ellipse est assez aplatie et les foyers sont bien séparés du centre. Voici le graphique :
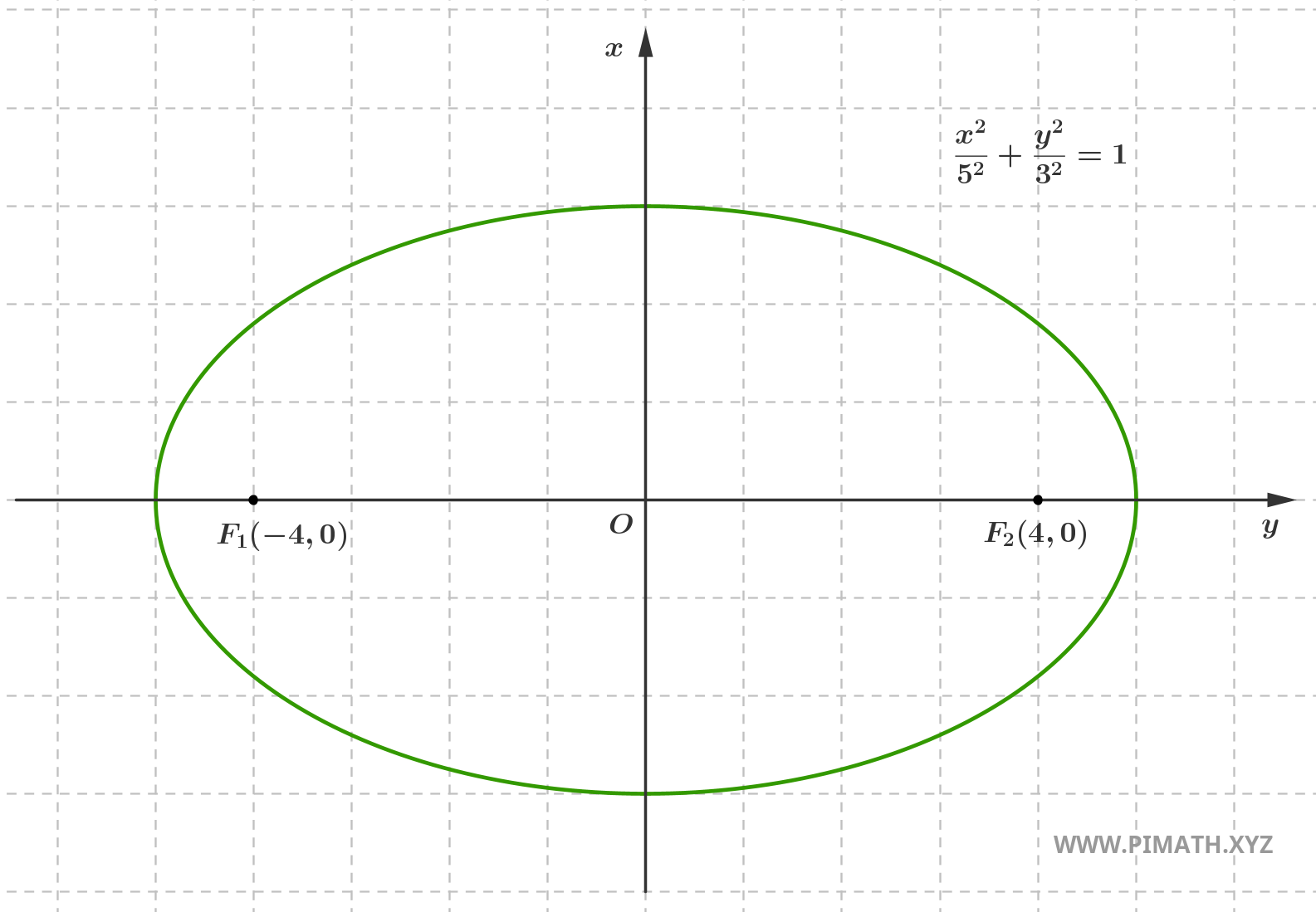
L'excentricité de l'ellipse est un concept qui met en relation la position des foyers avec la forme générale de la courbe. Ce n'est pas seulement une formule à mémoriser, mais un outil utile pour intuitivement visualiser à quel point l'ellipse est proche d'un cercle ou à quel point elle est allongée. Retenez : plus \( e \) est proche de zéro, plus l'ellipse ressemble à un cercle. Plus \( e \) est proche de \( 1 \), plus elle est aplatie et plus les foyers sont éloignés.
Exercices résolus
Exercice 1. Vérifier si le point \( P(3, 2) \) appartient à l'ellipse d'équation :
\[ \frac{x^2}{9} + \frac{y^2}{4} = 1 \]
Solution. Nous substituons \( x = 3 \), \( y = 2 \) :
\[ \frac{3^2}{9} + \frac{2^2}{4} = \frac{9}{9} + \frac{4}{4} = 1 + 1 = 2 \neq 1 \]
Cela signifie que le point n'appartient pas à l'ellipse.
Exercice 2. Une ellipse a son centre à l'origine, un grand axe horizontal, un demi-grand axe \( a = 5 \) et un demi-petit axe \( b = 3 \). Déterminer l'équation de l'ellipse.
Solution. L'équation canonique est
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{9} = 1 \]
Exercice 3. Déterminer la position des foyers de l'ellipse d'équation :
\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]
Trouver la distance des foyers \( c \).
Solution. De l'équation \( \displaystyle \frac{x^2}{16} + \displaystyle \frac{y^2}{9} = 1 \), nous identifions que le terme le plus grand (16) est sous \( x^2 \), donc le grand axe est horizontal.
Selon notre convention : \( a^2 = 16 \), \( b^2 = 9 \), donc \( a = 4 \), \( b = 3 \).
Nous calculons la distance des foyers \( c \) en utilisant :
\[ c^2 = a^2 - b^2 = 16 - 9 = 7 \Rightarrow c = \sqrt{7} \]
Les foyers se trouvent aux points \( F_1(-\sqrt{7}, 0) \), \( F_2(\sqrt{7}, 0) \).
Exercice 4. Écrire l'équation canonique de l'ellipse centrée à l'origine, à grand axe vertical, sachant que les sommets se trouvent aux points \( (0, \pm 6) \) et les foyers se trouvent aux points \( (0, \pm 4) \).
Solution. Si les sommets sont en \( (0, \pm 6) \), alors le demi-grand axe est \( a = 6 \), donc \( a^2 = 36 \).
Les foyers sont en \( (0, \pm 4) \), donc \( c = 4 \), donc \( c^2 = 16 \).
Nous calculons :
\[ b^2 = a^2 - c^2 = 36 - 16 = 20 \]
L'équation de l'ellipse, à grand axe vertical, est : \[ \displaystyle \frac{x^2}{b^2} + \displaystyle \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{20} + \frac{y^2}{36} = 1 \]
Exercice 5. Une ellipse a ses foyers aux points \( F_1(-3,0) \) et \( F_2(3,0) \), et passe par le point \( P(4,1) \). Déterminer l'équation canonique de l'ellipse.
Solution. Les foyers sont \( F_1(-3, 0) \), \( F_2(3, 0) \). Alors \( c = 3 \), donc \( c^2 = 9 \).
Le point \( P(4, 1) \) appartient à l'ellipse. Par définition : \[ |PF_1| + |PF_2| = 2a \] Nous calculons : \[ |PF_1| = \sqrt{(4 - (-3))^2 + (1 - 0)^2} = \sqrt{7^2 + 1^2} = \sqrt{49 + 1} = \sqrt{50} = 5\sqrt{2} \] \[ |PF_2| = \sqrt{(4 - 3)^2 + (1 - 0)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \] \[ \Rightarrow |PF_1| + |PF_2| = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \] \[ \Rightarrow 2a = 6\sqrt{2} \Rightarrow a = 3\sqrt{2} \Rightarrow a^2 = (3\sqrt{2})^2 = 9 \cdot 2 = 18 \] \[ b^2 = a^2 - c^2 = 18 - 9 = 9 \] L'équation de l'ellipse est donc : \[ \frac{x^2}{18} + \frac{y^2}{9} = 1 \]

