Équation de la droite

Soient \( P_1(x_1,y_1) \) et \( P_2(x_2,y_2) \) deux points distincts dans le plan cartésien. La droite passant par ces deux points a pour équation :

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

qui, en multipliant les deux membres par \( y_2 - y_1 \), devient :

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

• Similitude des triangles
• Interprétation géométrique
• Transformation en équation explicite
• Forme explicite de la droite
• Pente de la droite
• Interprétation de la pente
• Forme implicite de la droite
• Équation paramétrique de la droite
• Droite perpendiculaire
• Exercices

 Pour démontrer l'équation de la droite passant par deux points, considérons les points distincts \( P_1(x_1,y_1) \) et \( P_2(x_2,y_2) \) dans le plan cartésien. Nous voulons montrer que l'équation :

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

est satisfaite par chaque point \( P(x,y) \) appartenant à la droite.

Considérons les triangles dans la figure. Ils sont semblables par le critère de l'angle commun (angle entre la droite et l'axe des abscisses) et par la proportionnalité des côtés correspondants :

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

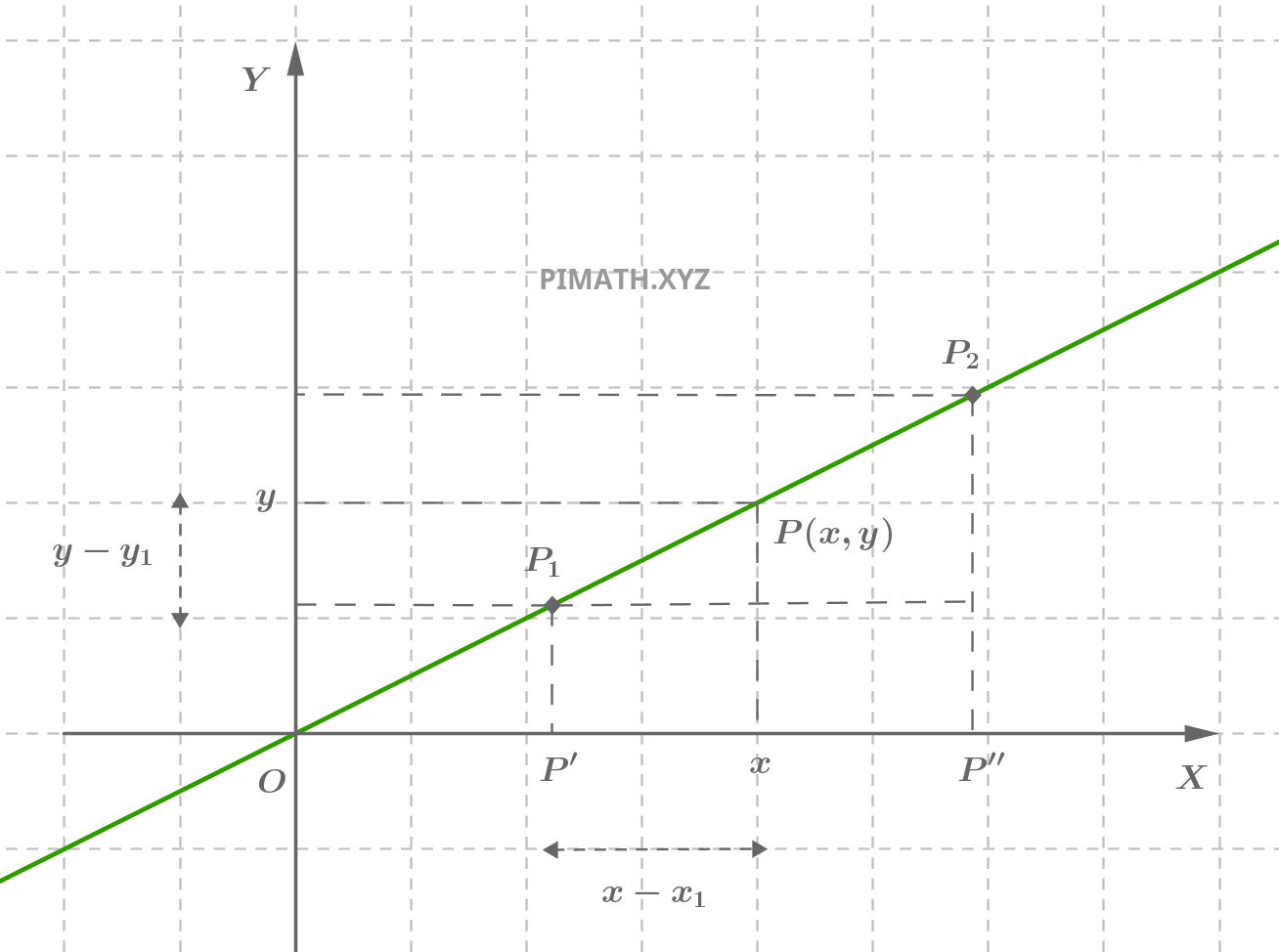
Cette relation découle directement de la propriété de similitude des triangles, garantissant que le rapport entre les différences des ordonnées et des abscisses reste constant le long de la droite.

La fraction \( \displaystyle \frac{y - y_1}{y_2 - y_1} \) représente le rapport entre la hauteur du point générique \( P \) par rapport à \( P_1 \) et la hauteur totale entre \( P_1 \) et \( P_2 \). De même, \( \displaystyle \frac{x - x_1}{x_2 - x_1} \) mesure le rapport analogue pour les abscisses. L'égalité entre ces deux rapports indique que le point \( P \) est aligné avec \( P_1 \) et \( P_2 \), c'est-à-dire qu'il se trouve sur la droite passant par ces deux points.

En multipliant les deux membres par \( y_2 - y_1 \), nous obtenons :

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

qui est l'équation de la droite sous forme explicite \( y = mx + q \), avec une pente \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \).

Cette forme de l'équation est fondamentale pour décrire la relation linéaire entre \( x \) et \( y \) pour tous les points de la droite passant par \( P_1 \) et \( P_2 \).

L'équation de la droite passant par deux points distincts \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \) peut être exprimée sous forme explicite comme suit :

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) \]

Cette équation met en relation la variable \( y \) avec la variable \( x \) le long de la droite. En d'autres termes, pour chaque valeur de \( x \) choisie, l'équation nous permet de déterminer la valeur correspondante de \( y \), qui est la coordonnée du point sur la droite.

Dans le contexte de cette équation, le terme :

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

représente la pente de la droite, c'est-à-dire le coefficient angulaire. La pente est une mesure de l'inclinaison de la droite par rapport à l'axe des abscisses (l'axe \( x \)). Si la pente est positive, la droite est croissante (monte de gauche à droite) ; si elle est négative, la droite est décroissante (descend de gauche à droite).

En d'autres termes, la pente décrit la vitesse à laquelle la droite croît ou décroît par rapport à l'axe horizontal \( x \). La pente est un paramètre crucial pour déterminer l'orientation de la droite dans le plan cartésien.

La pente \( m \) d'une droite passant par deux points \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \) est donnée par la formule :

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

La pente mesure l'inclinaison de la droite par rapport à l'axe des abscisses \( x \). Selon la valeur de la pente, nous pouvons faire les observations suivantes :

• Si \( m > 0 \), la droite est croissante, c'est-à-dire qu'elle monte de gauche à droite. Cela signifie que pour chaque augmentation de \( x \), \( y \) augmente également. La droite forme un angle aigu avec l'axe \( x \).
• Si \( m < 0 \), la droite est décroissante, c'est-à-dire qu'elle descend de gauche à droite. Dans ce cas, pour chaque augmentation de \( x \), la valeur de \( y \) diminue. La droite forme un angle obtus avec l'axe \( x \).
• Si \( x_2 = x_1 \), la pente est indéfinie, ce qui implique que la droite est verticale. Dans ce cas, il n'y a pas de changement horizontal (la différence entre les abscisses \( x_2 - x_1 \) est nulle), donc on ne peut pas définir une pente numérique. La droite est parallèle à l'axe \( y \) et n'a aucune inclinaison horizontale.

En général, la pente \( m \) nous offre des informations importantes sur le comportement de la droite. Si la droite est croissante, la valeur de \( y \) augmente quand \( x \) augmente ; si elle est décroissante, la valeur de \( y \) diminue quand \( x \) augmente ; si la droite est verticale, cela signifie que \( y \) ne dépend pas de \( x \) et la droite n'a aucune inclinaison horizontale.

Partant de la forme explicite de l'équation de la droite :

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

nous pouvons multiplier les deux membres par \( x_2 - x_1 \) pour obtenir une version plus générale et réécrire l'équation comme suit :

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

En multipliant les deux membres de l'équation par \( (x_2 - x_1) \), nous obtenons :

\[ (y - y_1)(x_2 - x_1) = (y_2 - y_1)(x - x_1). \]

En développant les termes, nous obtenons :

\[ (x_2 - x_1) y - (x_2 - x_1) y_1 = (y_2 - y_1) x - (y_2 - y_1) x_1 \]

Maintenant, pour obtenir une forme implicite, nous voulons regrouper les termes de manière à ce que l'équation soit sous une forme linéaire qui n'explicite pas \( y \). Nous déplaçons les termes contenant \( y \) et \( x \) d'un côté et les autres termes de l'autre :

\[ (y_2 - y_1) x - (x_2 - x_1) y = (y_2 - y_1) x_1 - (x_2 - x_1) y_1 \]

Nous écrivons cette équation sous la forme implicite standard :

\[ (y_2 - y_1) x - (x_2 - x_1) y + ((x_2 - x_1) y_1 - (y_2 - y_1) x_1) = 0 \]

C'est la forme implicite de l'équation de la droite. Si nous définissons les coefficients comme \( a = y_2 - y_1 \), \( b = -(x_2 - x_1) \), et \( c = (x_2 - x_1) y_1 - (y_2 - y_1) x_1 \), l'équation prend la forme générale :

\[ ax + by + c = 0 \]

Alternativement, si nous introduisons la pente \( m = \frac{y_2 - y_1}{x_2 - x_1} \) et réarrangeons les termes dans l'équation précédente, nous pouvons écrire :

\[ m(x_2 - x_1)x - (x_2 - x_1)y + ((x_2 - x_1)y_1 - m(x_2 - x_1)x_1) = 0 \]

En simplifiant et en divisant par \( (x_2 - x_1) \), nous obtenons :

\[ mx - y + (y_1 - mx_1) = 0. \]

Dans cette forme, les coefficients sont \( a = m \), \( b = -1 \), et \( c = y_1 - mx_1 \).

La forme implicite \( ax + by + c = 0 \) est une représentation plus générale d'une droite dans le plan cartésien. Ce format est utile principalement pour les applications géométriques et algébriques, où la valeur explicite de \( y \) n'est pas nécessaire ou lorsque l'on souhaite travailler directement avec les propriétés algébriques de la droite.

La droite passant par les points \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \) peut également être décrite sous forme paramétrique. Dans cette représentation, les coordonnées \( x \) et \( y \) d'un point sur la droite sont exprimées en fonction d'un paramètre réel \( t \), qui varie le long de la droite.

L'équation paramétrique de la droite est donnée par :

\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]

Ici, \( t \) est le paramètre qui peut prendre n'importe quelle valeur réelle. Lorsque \( t \) varie, le point \( (x, y) \) se déplace le long de la droite qui relie les deux points \( P_1 \) et \( P_2 \).

La forme paramétrique représente donc une famille de points sur la droite, où le paramètre \( t \) définit de manière unique chaque point de la droite. Lorsque \( t = 0 \), on obtient le point \( P_1(x_1, y_1) \) ; lorsque \( t = 1 \), on obtient le point \( P_2(x_2, y_2) \). Les valeurs de \( t \) entre 0 et 1 décrivent les points de la droite entre \( P_1 \) et \( P_2 \), tandis que les valeurs de \( t \) supérieures à 1 ou inférieures à 0 étendent la droite au-delà de ces points.

La formule paramétrique repose sur le concept de vecteur directeur, qui est le vecteur qui relie \( P_1 \) et \( P_2 \). En effet, la différence \( (x_2 - x_1, y_2 - y_1) \) est le vecteur directeur de la droite, et le paramètre \( t \) est le facteur d'échelle qui permet de se déplacer le long de la droite.

Sous forme vectorielle, l'équation paramétrique peut être écrite comme :

\[ \vec{r}(t) = \vec{P_1} + t \cdot (\vec{P_2} - \vec{P_1}), \]

où \( \vec{r}(t) \) représente la position d'un point générique sur la droite au temps \( t \), et \( \vec{P_1} \) et \( \vec{P_2} \) sont les vecteurs position des points \( P_1 \) et \( P_2 \), respectivement.

La forme paramétrique est particulièrement utile dans divers domaines de la géométrie analytique, comme l'étude des courbes, les applications en infographie, ou en physique pour décrire le mouvement d'un objet le long d'une trajectoire rectiligne.

Lorsque deux droites sont perpendiculaires, leur pente est liée par une relation bien précise. Si une droite a une pente \( m \), la pente de la droite perpendiculaire à celle-ci est donnée par :

\[ m_\perp = -\frac{1}{m}. \]

Cette formule exprime le fait que le produit des pentes de deux droites perpendiculaires est égal à \(-1\). La raison de cette relation peut être vue dans le fait que les angles formés par les deux droites doivent être de 90° (un angle droit), et donc la tangente de l'angle entre les droites doit satisfaire cette condition.

Pour trouver l'équation de la droite perpendiculaire passant par un point \( (x_1, y_1) \), nous pouvons utiliser la forme point-pente. La pente de la droite perpendiculaire est \( -\displaystyle \frac{1}{m} \), donc l'équation de la droite perpendiculaire sera :

\[ y - y_1 = -\frac{1}{m} (x - x_1). \]

Dans cette équation, \( (x_1, y_1) \) est le point par lequel passe la droite perpendiculaire, tandis que \( m \) est la pente de la droite originale. La formule décrit une droite qui a la pente opposée et inverse par rapport à la droite originale.

Si la droite originale est représentée par l'équation \( y = mx + q \), la droite perpendiculaire aura la pente \( m_\perp = -\displaystyle \frac{1}{m} \) et sera écrite sous la forme \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), où \( (x_1, y_1) \) est le point d'intersection entre la droite originale et la droite perpendiculaire.

Cette propriété des droites perpendiculaires est fondamentale dans de nombreux domaines de la géométrie, de la trigonométrie et de la physique, en particulier lorsqu'on étudie des angles et des trajectoires perpendiculaires entre elles.

Exercice 1: Détermine l'équation de la droite passant par \( A(1, 2) \) et \( B(3, 6) \).

Solution :

1. Calculons la pente de la droite : \[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
2. Utilisons l'équation point-pente pour déterminer l'équation de la droite passant par \( A(1, 2) \) et ayant une pente \( m = 2 \) : \[ y - 2 = 2(x - 1). \]
3. En développant l'équation : \[ y - 2 = 2x - 2. \]
4. En simplifiant : \[ y = 2x - 2 + 2 = 2x. \]

Ainsi, l'équation de la droite passant par les points \( A(1, 2) \) et \( B(3, 6) \) est \[ y = 2x. \]

Vérification: Nous pouvons vérifier que les deux points satisfont cette équation :

• Pour \( A(1, 2) \) : \[ 2 = 2 \cdot 1 = 2 \]
• Pour \( B(3, 6) \) : \[ 6 = 2 \cdot 3 = 6 \]

Exercice 2: Écris l'équation paramétrique de la droite passant par \( A(1, 2) \) et \( B(3, 6) \).

Solution :

1. Calculons le vecteur directeur \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), qui représente la direction de la droite : \[ \boldsymbol{v} = (3 - 1, 6 - 2) = (2, 4). \]
2. Les équations paramétriques de la droite sont : \[ \begin{cases} x = 1 + 2t \\ y = 2 + 4t \end{cases} \quad \text{avec} \quad t \in \mathbb{R}. \]