Le cercle est le lieu géométrique des points du plan qui sont à une distance constante d'un point fixe, appelé centre. Cette distance constante prend le nom de rayon. Le cercle est une courbe fermée, symétrique par rapport à son centre, et est un cas particulier de conique dégénérée obtenue en sectionnant un cône circulaire droit par un plan perpendiculaire à l'axe du cône.
Sommaire
- Définition Géométrique et Déduction de l'Équation
- Équation du Cercle avec Centre à l'Origine
- Équation du Cercle avec Centre Quelconque
- Forme Générale et Complétion du Carré
- Conditions pour Représenter un Cercle Réel
- Position d'un Point par Rapport au Cercle
- Droite Tangente au Cercle
- Intersection de Deux Cercles
- Faisceau de Cercles
- Symétries et Propriétés Géométriques
- Exercices Résolus
Définition Géométrique et Déduction de l'Équation
Considérons un point fixe \( C(x_0, y_0) \) dans le plan cartésien orthogonal. Le cercle de centre \( C \) et de rayon \( r > 0 \) est l'ensemble des points \( P(x, y) \) du plan tels que :
\[ d = \text{dist}(P, C) = r \]
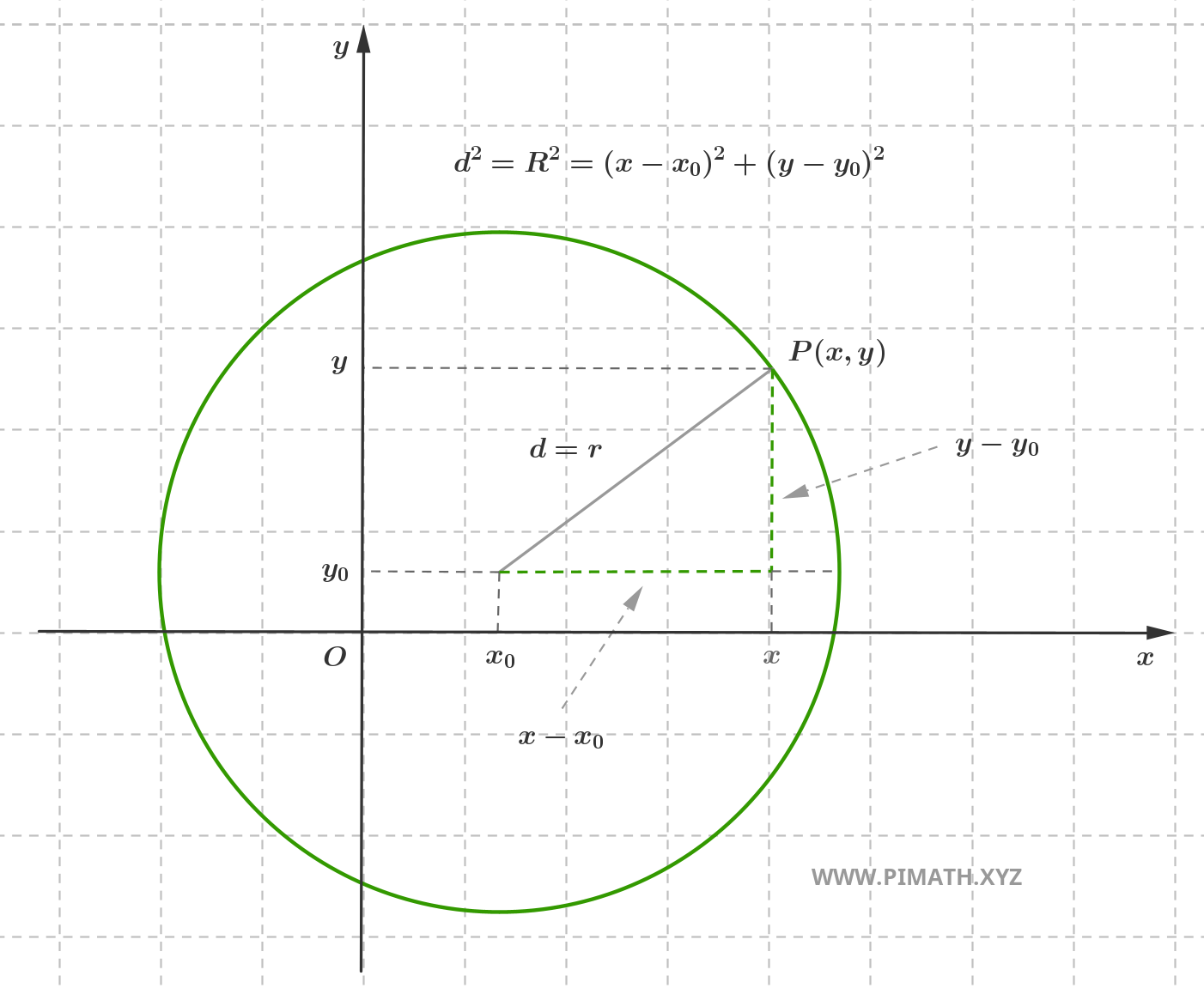
En appliquant la formule de la distance euclidienne entre deux points dans le plan cartésien, on a :
\[ \text{dist}(P, C) = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]
En imposant la condition \( \text{dist}(P, C) = r \), nous obtenons :
\[ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r \]
En élevant au carré les deux membres (opération licite puisque les deux sont non négatifs, \( r > 0 \) par définition) :
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Ceci est la forme canonique (ou forme normale) de l'équation du cercle de centre \( C(x_0, y_0) \) et de rayon \( r \). L'équation représente tous les points et seulement ceux qui satisfont la condition géométrique d'appartenance au cercle.
Équation du Cercle avec Centre à l'Origine
Dans le cas particulier où le centre coïncide avec l'origine du système de référence, c'est-à-dire \( C(0, 0) \), en posant \( x_0 = 0 \) et \( y_0 = 0 \) dans la forme canonique, l'équation se simplifie considérablement :
\[ x^2 + y^2 = r^2 \]
Ceci est l'équation la plus élémentaire du cercle et décrit l'ensemble de tous les points équidistants de l'origine des axes cartésiens. L'équation jouit des propriétés de symétrie suivantes :
- Symétrie par rapport à l'axe des abscisses : si \( (x, y) \) appartient au cercle, alors \( (x, -y) \) y appartient aussi
- Symétrie par rapport à l'axe des ordonnées : si \( (x, y) \) appartient au cercle, alors \( (-x, y) \) y appartient aussi
- Symétrie centrale par rapport à l'origine : si \( (x, y) \) appartient au cercle, alors \( (-x, -y) \) y appartient aussi
De plus, tous les diamètres du cercle passent par l'origine et ont pour longueur \( 2r \). Le point \( (r, 0) \) représente l'intersection du cercle avec le demi-axe positif des abscisses.
Équation du Cercle avec Centre Quelconque
Considérons maintenant le cas général d'un cercle de centre en un point arbitraire \( C(x_0, y_0) \) du plan et de rayon \( r > 0 \). L'équation canonique est :
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
En développant les carrés des binômes en utilisant les identités algébriques \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \), nous obtenons :
\[ x^2 - 2x \cdot x_0 + x_0^2 + y^2 - 2y \cdot y_0 + y_0^2 = r^2 \]
En réorganisant les termes et en portant toutes les quantités au premier membre :
\[ x^2 + y^2 - 2x_0 x - 2y_0 y + (x_0^2 + y_0^2 - r^2) = 0 \]
Nous introduisons maintenant les paramètres :
\[ D = -2x_0 \quad , \quad E = -2y_0 \quad , \quad F = x_0^2 + y_0^2 - r^2 \]
De ces relations nous pouvons tirer :
\[ x_0 = -\frac{D}{2} \quad , \quad y_0 = -\frac{E}{2} \quad , \quad r^2 = x_0^2 + y_0^2 - F = \frac{D^2 + E^2}{4} - F \]
En substituant dans la forme développée, nous obtenons la forme générale de l'équation du cercle :
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Forme Générale et Complétion du Carré
Étant donnée une équation sous la forme générale :
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
pour la ramener à la forme canonique et déterminer centre et rayon, nous utilisons la technique de la complétion du carré. La méthode consiste à transformer les expressions \( x^2 + Dx \) et \( y^2 + Ey \) en carrés parfaits.
Pour le terme en \( x \) :
\[ x^2 + Dx = x^2 + Dx + \frac{D^2}{4} - \frac{D^2}{4} = \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} \]
De manière analogue, pour le terme en \( y \) :
\[ y^2 + Ey = y^2 + Ey + \frac{E^2}{4} - \frac{E^2}{4} = \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} \]
En substituant dans l'équation générale :
\[ \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} + \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} + F = 0 \]
En réorganisant :
\[ \left( x + \frac{D}{2} \right)^2 + \left( y + \frac{E}{2} \right)^2 = \frac{D^2 + E^2}{4} - F \]
Ceci est la forme canonique, de laquelle nous pouvons lire directement :
- Centre : \( C\left( -\displaystyle \frac{D}{2}, -\displaystyle\frac{E}{2} \right) \)
- Rayon : \( r = \sqrt{\displaystyle\frac{D^2 + E^2}{4} - F} \) (pourvu que l'expression sous la racine soit positive)
Conditions pour Représenter un Cercle Réel
Une équation de la forme :
\[ ax^2 + by^2 + cxy + dx + ey + f = 0 \]
représente un cercle si et seulement si les conditions suivantes sont vérifiées :
- Coefficients des termes quadratiques égaux : \( a = b \neq 0 \)
- Absence du terme mixte : \( c = 0 \)
- Discriminant positif : \( \Delta = \displaystyle \frac{d^2 + e^2}{4a^2} - \displaystyle \frac{f}{a} > 0 \)
Dans le cas de la forme standard \( x^2 + y^2 + Dx + Ey + F = 0 \), la condition se réduit à :
\[ \frac{D^2 + E^2}{4} - F > 0 \quad \Leftrightarrow \quad D^2 + E^2 - 4F > 0 \]
Nous distinguons trois cas :
- Si \( D^2 + E^2 - 4F > 0 \) : l'équation représente un cercle réel de rayon \( r = \displaystyle \frac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
- Si \( D^2 + E^2 - 4F = 0 \) : l'équation représente un cercle dégénéré (un point)
- Si \( D^2 + E^2 - 4F < 0 \) : l'équation n'a pas de solutions réelles (cercle imaginaire)
Position d'un Point par Rapport au Cercle
Étant donné un cercle d'équation \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) et un point \( P(x_P, y_P) \), nous pouvons déterminer la position relative du point par rapport au cercle en calculant la quantité :
\[ \delta = (x_P - x_0)^2 + (y_P - y_0)^2 - r^2 \]
On a trois possibilités :
- Si \( \delta = 0 \) : le point appartient au cercle
- Si \( \delta < 0 \) : le point est intérieur au cercle
- Si \( \delta > 0 \) : le point est extérieur au cercle
De manière équivalente, en comparant la distance \( d = \sqrt{(x_P - x_0)^2 + (y_P - y_0)^2} \) du point au centre avec le rayon :
- Si \( d = r \) : point sur le cercle
- Si \( d < r \) : point intérieur
- Si \( d > r \) : point extérieur
Droite Tangente au Cercle
Étant donné un cercle de centre \( C(x_0, y_0) \) et de rayon \( r \), et un point \( P(x_1, y_1) \) appartenant au cercle, l'équation de la droite tangente au cercle au point \( P \) est :
\[ (x_1 - x_0)(x - x_0) + (y_1 - y_0)(y - y_0) = r^2 \]
Dans le cas particulier d'un cercle centré à l'origine \( x^2 + y^2 = r^2 \), l'équation de la tangente au point \( P(x_1, y_1) \) se simplifie en :
\[ x_1 x + y_1 y = r^2 \]
La droite tangente est perpendiculaire au rayon mené au point de tangence. Ce résultat dérive du fait que le vecteur \( \overrightarrow{CP} = (x_1 - x_0, y_1 - y_0) \) est normal à la tangente.
Tangentes d'un Point Extérieur
D'un point extérieur \( P(x_P, y_P) \) à un cercle, on peut mener exactement deux droites tangentes. Les points de tangence s'obtiennent en résolvant le système formé par l'équation du cercle et la condition que la distance du centre à la droite soit égale au rayon.
Intersection de Deux Cercles
Étant donnés deux cercles :
\[ \Gamma_1: \quad x^2 + y^2 + D_1 x + E_1 y + F_1 = 0 \] \[ \Gamma_2: \quad x^2 + y^2 + D_2 x + E_2 y + F_2 = 0 \]
Pour trouver les points d'intersection, nous résolvons le système formé par les deux équations. En soustrayant la seconde de la première, nous obtenons l'équation de l'axe radical :
\[ (D_1 - D_2)x + (E_1 - E_2)y + (F_1 - F_2) = 0 \]
L'axe radical est une droite qui, lorsque les cercles s'intersectent, passe par les deux points d'intersection. Les positions relatives des cercles dépendent de la distance \( d \) entre les centres et des rayons \( r_1, r_2 \) :
- Si \( d > r_1 + r_2 \) : cercles extérieurs (aucune intersection)
- Si \( d = r_1 + r_2 \) : cercles tangents extérieurement (un point d'intersection)
- Si \( |r_1 - r_2| < d < r_1 + r_2 \) : cercles sécants (deux points d'intersection)
- Si \( d = |r_1 - r_2| \) : cercles tangents intérieurement (un point d'intersection)
- Si \( d < |r_1 - r_2| \) : un cercle intérieur à l'autre (aucune intersection)
Faisceau de Cercles
Un faisceau de cercles est un ensemble de cercles dépendant d'un paramètre. Le faisceau engendré par deux cercles \( \Gamma_1 \) et \( \Gamma_2 \) a pour équation :
\[ \lambda \Gamma_1 + \mu \Gamma_2 = 0 \]
où \( \lambda \) et \( \mu \) sont des paramètres réels non tous deux nuls. Explicitement :
\[ \lambda(x^2 + y^2 + D_1 x + E_1 y + F_1) + \mu(x^2 + y^2 + D_2 x + E_2 y + F_2) = 0 \]
On distingue différents types de faisceaux :
- Faisceau elliptique : les cercles de base ne s'intersectent pas ; tous les cercles du faisceau sont réels
- Faisceau parabolique : les cercles de base sont tangents ; le faisceau contient des droites (cercles dégénérés)
- Faisceau hyperbolique : les cercles de base s'intersectent en deux points ; le faisceau contient des cercles réels et imaginaires
Symétries et Propriétés Géométriques
Le cercle possède de remarquables propriétés de symétrie qui en font une figure géométrique d'un intérêt particulier :
Symétries
- Symétrie centrale : tout cercle est symétrique par rapport à son propre centre
- Axes de symétrie : toute droite passant par le centre est un axe de symétrie
- Invariance par rotation : le cercle est invariant pour toute rotation autour du centre
Propriétés Métriques
- Longueur (circonférence) : \( C = 2\pi r \)
- Aire du disque : \( A = \pi r^2 \)
- Angle au centre et inscrit : un angle inscrit vaut la moitié de l'angle au centre correspondant
Exercices Résolus
Exercice 1. Vérifier si le point \( P(3, 4) \) appartient au cercle d'équation \( x^2 + y^2 = 25 \).
Solution. Nous substituons les coordonnées du point dans l'équation :
\[ 3^2 + 4^2 = 9 + 16 = 25 \]
Puisque l'égalité est vérifiée, le point \( P(3, 4) \) appartient au cercle. Géométriquement, cela signifie que la distance de \( P \) à l'origine est exactement égale au rayon \( r = 5 \).
Exercice 2. Déterminer l'équation du cercle de centre \( C(2, -3) \) et de rayon \( r = 4 \).
Solution. En appliquant la forme canonique :
\[ (x - 2)^2 + (y - (-3))^2 = 4^2 \] \[ (x - 2)^2 + (y + 3)^2 = 16 \]
En développant, nous obtenons la forme générale :
\[ x^2 - 4x + 4 + y^2 + 6y + 9 = 16 \] \[ x^2 + y^2 - 4x + 6y - 3 = 0 \]
Exercice 3. Étant donnée l'équation \( x^2 + y^2 + 6x - 8y + 5 = 0 \), déterminer centre et rayon du cercle.
Solution. Nous complétons les carrés :
\[ x^2 + 6x = (x + 3)^2 - 9 \] \[ y^2 - 8y = (y - 4)^2 - 16 \]
En substituant :
\[ (x + 3)^2 - 9 + (y - 4)^2 - 16 + 5 = 0 \] \[ (x + 3)^2 + (y - 4)^2 = 20 \]
Donc :
- Centre : \( C(-3, 4) \)
- Rayon : \( r = \sqrt{20} = 2\sqrt{5} \)
Exercice 4. Trouver l'équation du cercle passant par les points \( A(1, 0) \), \( B(0, 1) \) et \( C(-1, 0) \).
Solution. Nous utilisons la forme générale \( x^2 + y^2 + Dx + Ey + F = 0 \) et imposons le passage par les trois points :
Pour \( A(1, 0) \) :
\[ 1 + 0 + D + 0 + F = 0 \implies D + F = -1 \]
Pour \( B(0, 1) \) :
\[ 0 + 1 + 0 + E + F = 0 \implies E + F = -1 \]
Pour \( C(-1, 0) \) :
\[ 1 + 0 - D + 0 + F = 0 \implies -D + F = -1 \]
En résolvant le système :
\[ \begin{cases} D + F = -1 \\ E + F = -1 \\ -D + F = -1 \end{cases} \]
De la première et troisième équation : \( D = 0 \), donc \( F = -1 \). De la deuxième équation : \( E = 0 \).
L'équation cherchée est : \( x^2 + y^2 - 1 = 0 \), soit \( x^2 + y^2 = 1 \).
Ceci est le cercle unité centré à l'origine.
Exercice 5. Déterminer les tangentes au cercle \( x^2 + y^2 = 9 \) menées du point extérieur \( P(5, 0) \).
Solution. Soit \( T(x_T, y_T) \) un point de tangence. La droite \( PT \) a pour équation de la tangente au point \( T \) :
\[ x_T x + y_T y = 9 \]
Puisque cette droite passe par \( P(5, 0) \) :
\[ 5x_T + 0 \cdot y_T = 9 \Rightarrow x_T = \frac{9}{5} \]
\( T \) étant sur le cercle : \( x_T^2 + y_T^2 = 9 \), donc :
\[ \left(\frac{9}{5}\right)^2 + y_T^2 = 9 \Rightarrow y_T^2 = 9 - \frac{81}{25} = \frac{144}{25} \Rightarrow y_T = \pm\frac{12}{5} \]
Les points de tangence sont :
\[ T_1\left(\frac{9}{5}, \frac{12}{5}\right) \quad \text{et} \quad T_2\left(\frac{9}{5}, -\frac{12}{5}\right) \]
Les équations des tangentes sont :
\[ \frac{9}{5}x + \frac{12}{5}y = 9 \quad \implies \quad 3x + 4y = 15 \] \[ \frac{9}{5}x - \frac{12}{5}y = 9 \quad \implies \quad 3x - 4y = 15 \]

