Équations du Second Degré

Une équation est du second degré si et seulement si elle peut être écrite sous la forme suivante, appelée forme canonique :

\[ a x^2 + b x + c = 0 \quad , \quad a \neq 0 \]

Les nombres réels \( a, b \) et \( c \) sont appelés respectivement coefficient quadratique, linéaire et constant.

On peut toujours supposer que le coefficient quadratique est positif. En effet, si \( a < 0 \), il suffit de multiplier les deux membres de l'équation par \( -1 \) pour revenir au cas \( a > 0 \).

Table des matières

• Complétion du carré
• Formule réduite
• Équations du second degré monomiales
• Équations du second degré pures
• Équations du second degré fausses
• Relation entre la somme et le produit des racines
• Exercices résolus
• Signification géométrique

Dans cette section, nous déduirons la formule générale pour résoudre toute équation du second degré. Commençons par la forme canonique :

\[ ax^2 + bx + c = 0, \quad a \neq 0 \]

Pour simplifier les calculs, nous divisons tous les termes par \( a \), de manière à rendre le coefficient du terme quadratique égal à 1 :

\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]

Maintenant, isolons le terme constant en le déplaçant à droite :

\[ x^2 + \frac{b}{a}x = -\frac{c}{a} \]

À ce stade, appliquons la méthode de la complétion du carré. Le truc consiste à ajouter et à soustraire le terme correct pour transformer le premier membre en un carré parfait. Ce terme est :

\[ \left(\frac{b}{2a}\right)^2 \]

Ajoutons-le des deux côtés de l'équation :

\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 \]

Le premier membre est maintenant le carré d'un binôme :

\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2} \]

Réécrivons le second membre avec un dénominateur commun :

\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} \]

Maintenant, extrayons la racine carrée des deux membres, en nous rappelant que la racine d'un carré est la valeur absolue :

\[ \left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a} \]

Nous en déduisons directement \( x \) :

\[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]

Enfin, isolons \( x \) et obtenons la célèbre formule de résolution :

\[ x_{1,2} = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]

Le terme sous la racine, appelé discriminant et noté \( \Delta \), est défini comme suit :

\[ \Delta = b^2 - 4ac \]

Mais qu'est-ce que représente le discriminant ? Il nous permet de comprendre d'un coup d'œil le type de solutions que l'équation aura. Examinons-le dans les trois cas possibles :

• \( \Delta > 0 \) : le discriminant est positif, donc la racine est un nombre réel. Cela signifie que l'équation a deux solutions réelles distinctes.
• \( \Delta = 0 \) : la racine carrée de zéro est zéro, donc la formule nous donne une seule solution répétée. En d'autres termes, l'équation a deux solutions identiques (ou une solution double).
• \( \Delta < 0 \) : la racine d'un nombre négatif n'est pas un nombre réel, donc l'équation n'a pas de solutions réelles, mais deux solutions complexes avec une partie imaginaire.

Cela signifie que, rien qu'en regardant la valeur de \( \Delta \), nous pouvons prédire la nature des solutions sans avoir à résoudre directement l'équation.

La formule réduite est une version simplifiée de la formule de résolution des équations du second degré, utile lorsque le coefficient \( b \) est pair.

Considérons une équation du second degré sous forme canonique :

\[ ax^2 + bx + c = 0 \]

Si le coefficient \( b \) est pair, nous pouvons l'écrire sous la forme :

\[ b = 2k \]

En substituant dans l'équation, nous obtenons :

\[ ax^2 + 2kx + c = 0 \]

La formule de résolution classique est :

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

En substituant \( b = 2k \) :

\[ x = \frac{-2k \pm \sqrt{(2k)^2 - 4ac}}{2a} \]

\[ x = \frac{-2k \pm \sqrt{4k^2 - 4ac}}{2a} \]

\[ x = \frac{-2k \pm 2\sqrt{k^2 - ac}}{2a} \]

En divisant le numérateur et le dénominateur par 2 :

\[ x = \frac{-k \pm \sqrt{k^2 - ac}}{a} \]

Enfin, nous pouvons exprimer la formule réduite comme suit :

\[ x = \frac{-\frac{b}{2} \pm \sqrt{\left(\frac{b}{2}\right)^2 - ac}}{a} \]

Le discriminant réduit est donné par :

\[ \Delta' = \left(\frac{b}{2}\right)^2 - ac \]

Comparons-le maintenant avec le discriminant de la formule complète :

\[ \Delta = b^2 - 4ac \]

En substituant \( b = 2k \), nous obtenons :

\[ \Delta = (2k)^2 - 4ac \]

\[ \Delta = 4k^2 - 4ac \]

En divisant tout par 4 :

\[ \frac{\Delta}{4} = k^2 - ac \]

Puisque \( k = \displaystyle \frac{b}{2} \), nous pouvons réécrire :

\[ \frac{\Delta}{4} = \left(\frac{b}{2}\right)^2 - ac \]

Ce qui correspond exactement à la définition de \( \Delta' \).

Ainsi, nous pouvons conclure que :

\[ \Delta' = \frac{\Delta}{4} \]

Une équation est dite monomiale si elle se réduit à un seul terme quadratique, c'est-à-dire sous la forme :

\[ ax^2 = 0 \]

Pour résoudre cette équation, nous divisons les deux membres par \( a \) (en supposant \( a \neq 0 \)) :

\[ x^2 = 0 \]

En extrayant la racine carrée, nous obtenons la solution :

\[ x = 0 \]

Bien que la valeur soit unique, mathématiquement, on considère deux solutions confondues : \( x_1 = x_2 = 0 \).

Une équation est dite pure si, sous la forme générale \( ax^2 + bx + c = 0 \), le coefficient \( b \) est nul, se réduisant à :

\[ ax^2 + c = 0 \]

Pour résoudre cette équation, nous déplaçons le terme constant \( c \) dans le deuxième membre :

\[ ax^2 = -c \]

Nous divisons les deux membres par \( a \) :

\[ x^2 = -\frac{c}{a} \]

Les solutions existent seulement si \( \displaystyle -\frac{c}{a} \geq 0 \), sinon l’équation n’a pas de solutions réelles. Si la valeur sous la racine est positive, nous obtenons :

\[ x_{1,2} = \pm \sqrt{-\frac{c}{a}} \]

Une équation est dite spurielle si le terme constant est nul, c'est-à-dire :

\[ ax^2 + bx = 0 \]

Dans ce cas, nous pouvons la résoudre en factorisant \( x \) comme facteur commun :

\[ x (ax + b) = 0 \]

En appliquant la loi de l'annulation du produit, nous obtenons les deux solutions :

\[ x = 0 \quad \text{ou} \quad x = -\frac{b}{a} \]

Ces solutions peuvent également être trouvées en appliquant la formule générale de résolution des équations du second degré.

Considérons l'équation quadratique de la forme \( ax^2 + bx + c = 0 \), où \( a \), \( b \) et \( c \) sont les coefficients. Soient \( x_1 \) et \( x_2 \) les racines de cette équation. Nous voulons maintenant écrire l'équation en termes des racines. Une équation du second degré peut être écrite comme le produit des facteurs \( (x - x_1) \) et \( (x - x_2) \), nous pouvons donc écrire :

\[ a(x - x_1)(x - x_2) = 0 \]

En développant le produit à gauche, nous obtenons :

\[ a(x^2 - (x_1 + x_2)x + x_1x_2) = 0 \]

Maintenant, en appliquant la distributivité, nous multiplions \( a \) sur chaque terme, ce qui donne :

\[ ax^2 - a(x_1 + x_2)x + ax_1x_2 = 0 \]

À ce stade, nous pouvons comparer cette expression avec l'équation originale \( ax^2 + bx + c = 0 \). En particulier, nous voyons que les coefficients doivent être égaux. En comparant le terme linéaire, nous obtenons :

\[ -a(x_1 + x_2) = b \]

En résolvant pour \( x_1 + x_2 \), nous obtenons :

\[ x_1 + x_2 = -\frac{b}{a} \]

De même, en comparant le terme constant, nous obtenons :

\[ ax_1x_2 = c \]

En résolvant pour le produit des racines, nous obtenons :

\[ x_1 \cdot x_2 = \frac{c}{a} \]

En résumé, les racines \( x_1 \) et \( x_2 \) sont liées aux coefficients \( a \), \( b \) et \( c \) par ces deux relations simples : la somme des racines est \( \displaystyle -\frac{b}{a} \) et le produit des racines est \( \displaystyle \frac{c}{a} \). Ces propriétés sont fondamentales et nous permettent de déduire des informations importantes sur les racines sans les calculer directement.

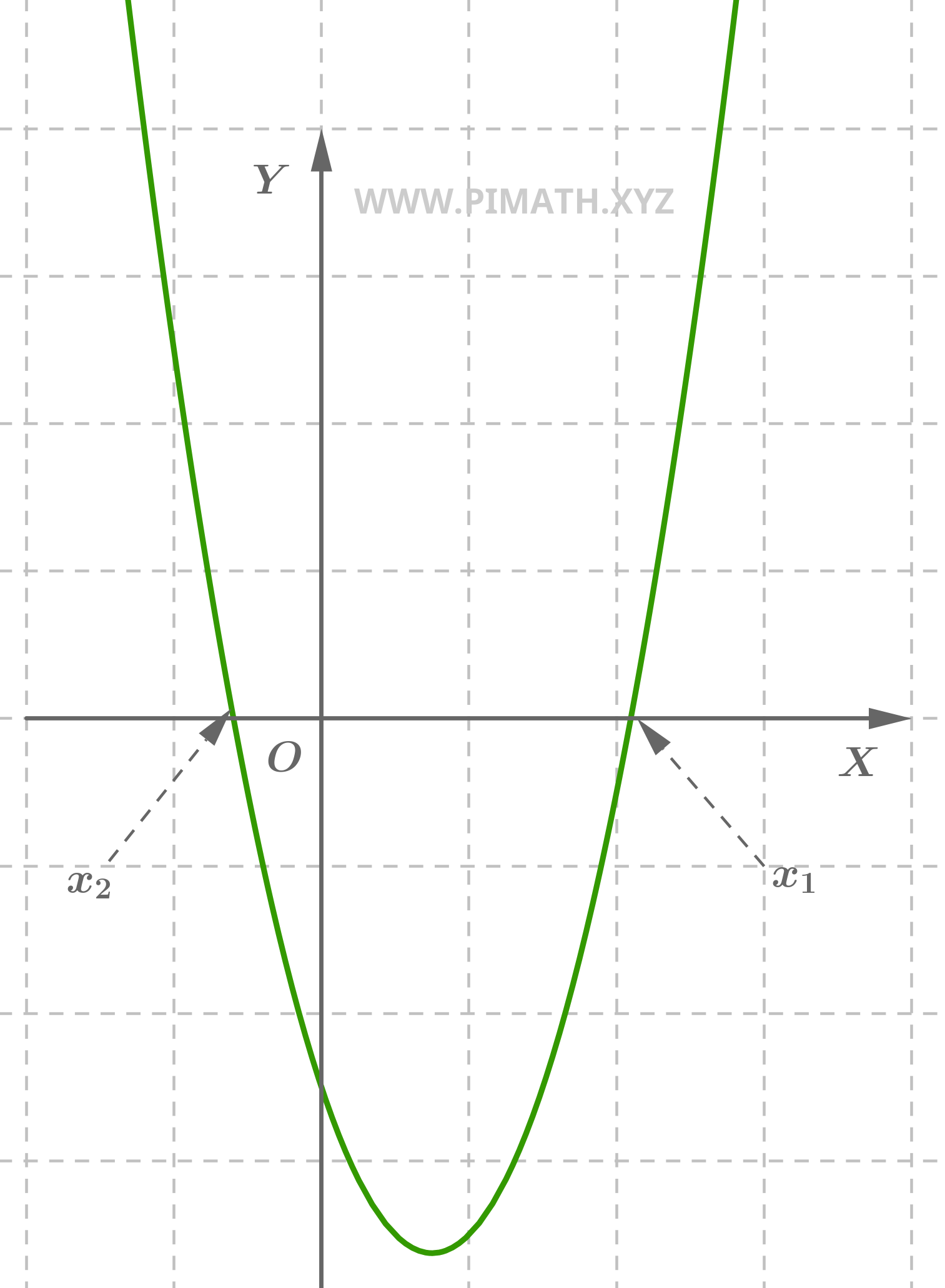
Exercice 1. Résoudre l'équation du second degré \( x^2 - 3x - 5 = 0 \).

Solution. Pour la résoudre, nous utilisons la formule suivante :

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Dans ce cas, les coefficients sont \( a = 1 \), \( b = -3 \) et \( c = -5 \). En appliquant la formule :

\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-5)}}{2(1)} = \frac{3 \pm \sqrt{9 + 20}}{2} = \frac{3 \pm \sqrt{29}}{2} \]

Les solutions sont donc :

\[ x_1 = \frac{3 + \sqrt{29}}{2} \quad , \quad x_2 = \frac{3 - \sqrt{29}}{2} \]

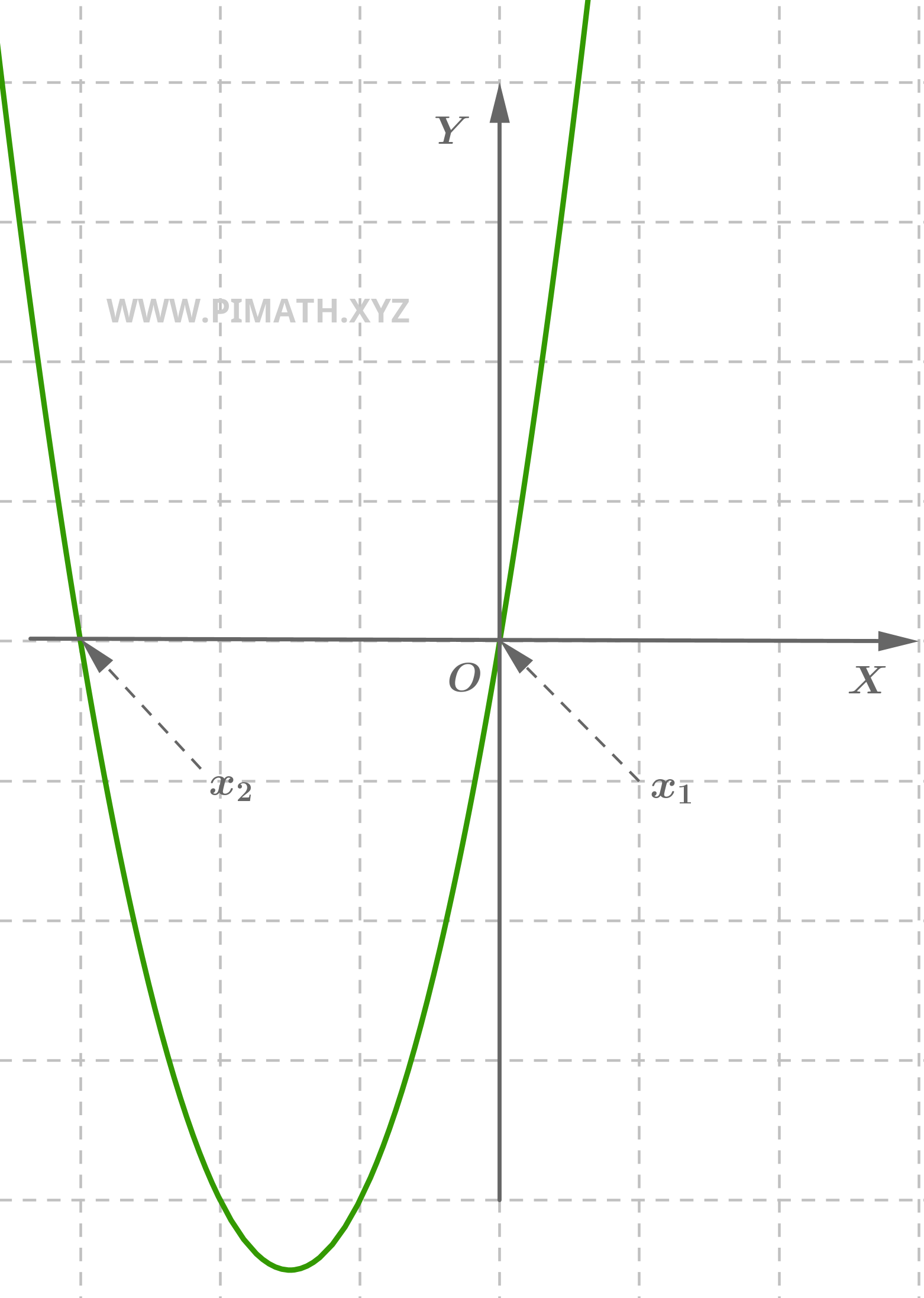
Exercice 2 (forme réduite). Trouver les solutions de l'équation suivante \( x^2 + 6x = 0 \).

Solution. Pour la résoudre, nous pouvons factoriser :

\[ x(x + 6) = 0 \]

Les solutions sont donc : \( x_1 = 0 \) et \( x_2 = -6 \).

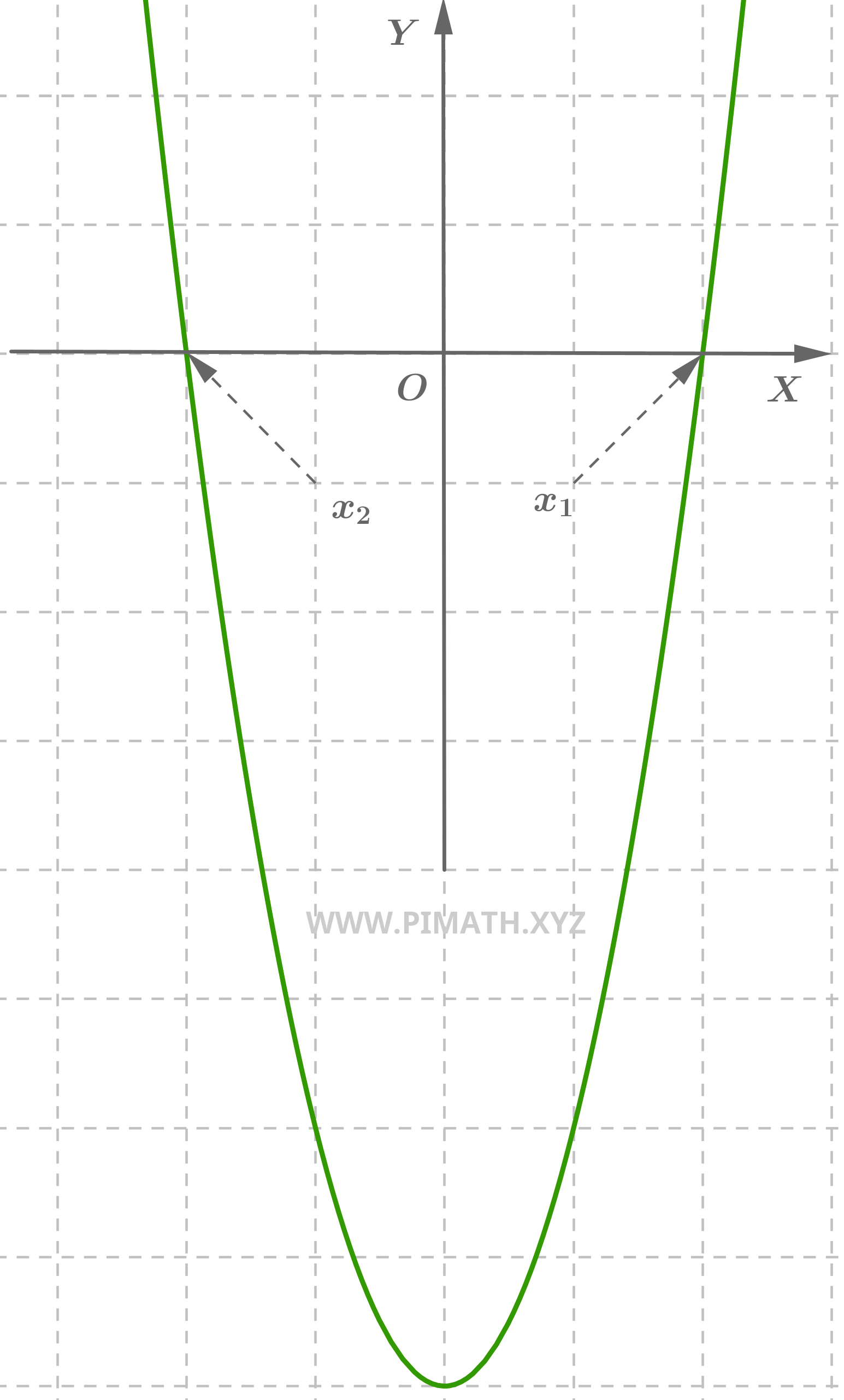
Exercice 3 (équation monomiale). Trouver les solutions de l'équation \( x^2 = 16 \).

Solution. Pour la résoudre, nous pouvons extraire la racine carrée des deux membres :

\[ x = \pm \sqrt{16} = \pm 4 \]

Les solutions sont donc : \( x_1 = 4 \) et \( x_2 = -4 \).

Exercice 4 (équation pure). Trouver les solutions de l'équation \( x^2 + 9 = 0 \).

Solution. Isolons \( x^2 \) :

\[ x^2 = -9 \]

Comme il n'existe pas de nombres réels qui satisfont cette équation, il n'y a pas de solutions réelles.

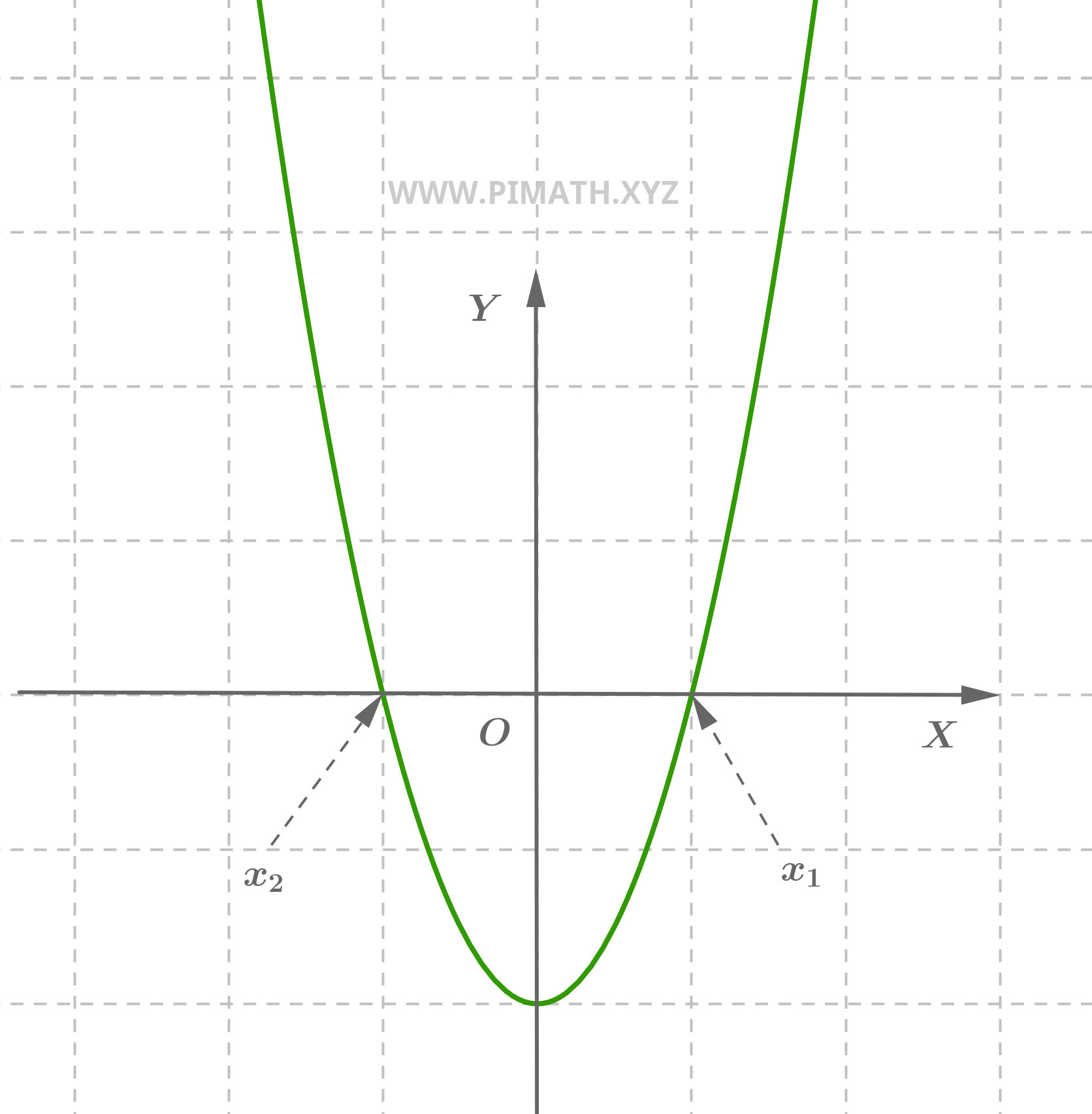
Exercice 5. Trouver les solutions de l'équation suivante \( x^2 - 4 = 0 \).

Solution. Isolons \( x^2 \) :

\[ x^2 = 4 \]

Maintenant, extrayons la racine carrée des deux membres :

\[ x = \pm \sqrt{4} = \pm 2 \]

Les solutions sont donc :

\[ x_1 = 2 \quad , \quad x_2 = -2 \]

Du point de vue géométrique, résoudre une équation du second degré signifie trouver les valeurs réelles (si elles existent) pour lesquelles la parabole de l'équation \( y = ax^2 + bx + c \) coupe l'axe des abscisses \( x \) ou, si vous voulez, la droite \( y = 0 \).