Une équation est du second degré si et seulement si elle peut s'écrire sous la forme suivante :
\[ a x ^ 2 + b x + c = 0 \quad , \quad a \neq 0 \]
appelée forme canonique. Les nombres réels \( a , b \) et \( c \) portent le nom de coefficient quadratique, linéaire et terme constant.
On peut toujours supposer que le coefficient quadratique est strictement positif. En effet, dans le cas où \( a < 0 \), il suffit de multiplier les deux membres par \( -1 \) pour se ramener au cas \( a > 0 \).
Sommaire
- Complétion du Carré
- Formule Réduite
- Équations du Second Degré Monômes
- Équations du Second Degré Pures
- Équations du Second Degré Incomplètes
- Relations entre Somme et Produit des Racines
- Exercices Résolus
- Signification Géométrique
Complétion du Carré
Dans cette section, nous déduirons la formule générale pour résoudre n'importe quelle équation du second degré. Partons de la forme canonique :
\[ ax^2 + bx + c = 0, \quad a \neq 0 \]
Pour simplifier les calculs, divisons tout par \( a \), de sorte à rendre le coefficient du terme quadratique égal à 1 :
\[ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 \]
Maintenant, isolons le terme constant en le portant au second membre :
\[ x^2 + \frac{b}{a}x = -\frac{c}{a} \]
À ce stade, appliquons la méthode de complétion du carré. L'astuce consiste à ajouter et retrancher une quantité pour transformer le premier membre en un carré parfait. Dans ce cas, le terme manquant est
\[ \left(\frac{b}{2a}\right)^2 \]
Ajoutons-le aux deux membres :
\[ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 \]
Le premier membre est maintenant le carré d'un binôme, nous pouvons donc l'écrire comme
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2} \]
Réécrivons le second membre avec un dénominateur commun :
\[ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} \]
Nous pouvons maintenant extraire la racine carrée des deux membres, en rappelant que \( \sqrt{x^2} = |x| \) :
\[ \left| x + \frac{b}{2a} \right| = \frac{\sqrt{b^2 - 4ac}}{2a} \]
De là, nous obtenons directement \( x \) :
\[ x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
Enfin, isolons \( x \) et obtenons la célèbre formule résolutive :
\[ x_{1,2} = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} \]
Le terme sous la racine, connu sous le nom de discriminant et noté \( \Delta \), est défini comme :
\[ \Delta = b^2 - 4ac \]
Mais que représente le discriminant ? Il nous permet de déterminer d'un coup d'œil le type de solutions que possèdera l'équation. Analysons-le dans les trois cas possibles :
- \( \Delta > 0 \) : le discriminant est positif, donc la racine est un nombre réel. Cela signifie que l'équation possède deux solutions réelles et distinctes.
- \( \Delta = 0 \) : la racine carrée de zéro est zéro, donc la formule nous donne une seule solution répétée. En d'autres termes, l'équation possède deux solutions confondues (ou une solution double).
- \( \Delta < 0 \) : la racine d'un nombre négatif n'est pas un nombre réel, donc l'équation n'a pas de solutions réelles, mais deux solutions complexes avec partie imaginaire.
Cela signifie qu'en regardant seulement la valeur de \( \Delta \), nous pouvons prédire la nature des solutions sans avoir à résoudre directement l'équation.
Formule Réduite
La formule réduite est une version simplifiée de la formule résolutive des équations du second degré, utile lorsque le coefficient \( b \) est pair.
Considérons une équation du second degré sous la forme canonique :
\[ ax^2 + bx + c = 0 \]
Si le coefficient \( b \) est pair, nous pouvons l'écrire comme :
\[ b = 2k \]
En substituant dans l'équation, nous obtenons :
\[ ax^2 + 2kx + c = 0 \]
La formule résolutive classique est :
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
En substituant \( b = 2k \) :
\[ x = \frac{-2k \pm \sqrt{(2k)^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm \sqrt{4k^2 - 4ac}}{2a} \]
\[ x = \frac{-2k \pm 2\sqrt{k^2 - ac}}{2a} \]
En divisant numérateur et dénominateur par 2 :
\[ x = \frac{-k \pm \sqrt{k^2 - ac}}{a} \]
Finalement, nous pouvons exprimer la formule réduite comme :
\[ x = \frac{-\frac{b}{2} \pm \sqrt{\left(\frac{b}{2}\right)^2 - ac}}{a} \]
Le discriminant réduit est donné par :
\[ \Delta' = \left(\frac{b}{2}\right)^2 - ac \]
Comparons-le maintenant avec le discriminant de la formule complète :
\[ \Delta = b^2 - 4ac \]
En substituant \( b = 2k \), nous obtenons :
\[ \Delta = (2k)^2 - 4ac \]
\[ \Delta = 4k^2 - 4ac \]
En divisant tout par 4 :
\[ \frac{\Delta}{4} = k^2 - ac \]
Puisque \( k = \displaystyle \frac{b}{2} \), nous pouvons réécrire :
\[ \frac{\Delta}{4} = \left(\frac{b}{2}\right)^2 - ac \]
qui est exactement la définition de \( \Delta' \).
Nous pouvons donc conclure que :
\[ \Delta' = \frac{\Delta}{4} \]
Équations du Second Degré Monômes
Une équation est dite monôme si elle se réduit à un seul terme quadratique, c'est-à-dire de la forme :
\[ ax^2 = 0 \]
Pour résoudre cette équation, divisons les deux membres par \( a \) (en supposant \( a \neq 0 \)) :
\[ x^2 = 0 \]
En extrayant la racine carrée, nous obtenons la solution :
\[ x = 0 \]
Bien que la valeur soit unique, mathématiquement on considère deux solutions confondues : \( x_1 = x_2 = 0 \).
Équations du Second Degré Pures
Une équation est dite pure si, dans la forme générale \( ax^2 + bx + c = 0 \), le coefficient \( b \) est nul, se réduisant à :
\[ ax^2 + c = 0 \]
Pour résoudre cette équation, portons le terme constant \( c \) au second membre :
\[ ax^2 = -c \]
Divisons les deux membres par \( a \neq 0 \) :
\[ x^2 = -\frac{c}{a} \]
Les solutions existent seulement si \( \displaystyle -\frac{c}{a} \geq 0 \), sinon l'équation n'a pas de solutions réelles. Si la valeur sous la racine est positive, nous obtenons :
\[ x_{1,2} = \pm \sqrt{-\frac{c}{a}} \]
Équations du Second Degré Incomplètes
Une équation est dite incomplète si le terme constant est nul, c'est-à-dire :
\[ ax^2 + bx = 0 \]
Dans ce cas, nous pouvons la résoudre en factorisant \( x \) comme facteur commun :
\[ x (ax + b) = 0 \]
En appliquant la loi d'annulation du produit, nous obtenons les deux solutions :
\[ x = 0 \quad \text{ou bien} \quad x = -\frac{b}{a} \]
Relations entre Somme et Produit des Racines
Considérons l'équation quadratique du type \( ax^2 + bx + c = 0 \), où \( a \), \( b \) et \( c \) sont les coefficients. Soient \( x_1 \) et \( x_2 \) les racines de cette équation. Nous voulons maintenant écrire l'équation en termes des racines. Une équation du second degré peut s'écrire comme le produit des facteurs \( (x - x_1) \) et \( (x - x_2) \), nous pouvons donc écrire :
\[ a(x - x_1)(x - x_2) = 0 \]
En développant le produit à gauche, nous obtenons :
\[ a(x^2 - (x_1 + x_2)x + x_1x_2) = 0 \]
Maintenant, par la propriété distributive, nous obtenons :
\[ ax^2 - a(x_1 + x_2)x + ax_1x_2 = 0 \]
À ce stade, nous pouvons comparer cette expression avec l'équation canonique \( ax^2 + bx + c = 0 \). En particulier, nous voyons que les coefficients doivent être égaux. En comparant le terme linéaire, nous obtenons :
\[ -a(x_1 + x_2) = b \]
En résolvant pour \( x_1 + x_2 \), nous obtenons :
\[ x_1 + x_2 = -\frac{b}{a} \]
De même, en comparant le terme constant, nous obtenons :
\[ ax_1x_2 = c \]
En résolvant pour le produit des racines, nous obtenons :
\[ x_1 \cdot x_2 = \frac{c}{a} \]
En résumé, les racines \( x_1 \) et \( x_2 \) sont liées aux coefficients \( a \), \( b \) et \( c \) par ces deux relations simples : la somme des racines est \( \displaystyle -\frac{b}{a} \) et le produit des racines est \( \displaystyle \frac{c}{a} \). Ces propriétés sont fondamentales et nous permettent de déduire des informations importantes sur les racines sans les calculer directement.
Exercices Résolus
Exercice 1. Résoudre l'équation du second degré \( x^2 - 3x - 5 = 0 \).
Solution. Pour la résoudre, utilisons la formule suivante :
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Dans ce cas, les coefficients sont \( a = 1 \), \( b = -3 \) et \( c = -5 \). En appliquant la formule :
\[ x = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(1)(-5)}}{2(1)} = \frac{3 \pm \sqrt{9 + 20}}{2} = \frac{3 \pm \sqrt{29}}{2} \]
Les solutions sont donc :
\[ x_1 = \frac{3 + \sqrt{29}}{2} \quad , \quad x_2 = \frac{3 - \sqrt{29}}{2} \]
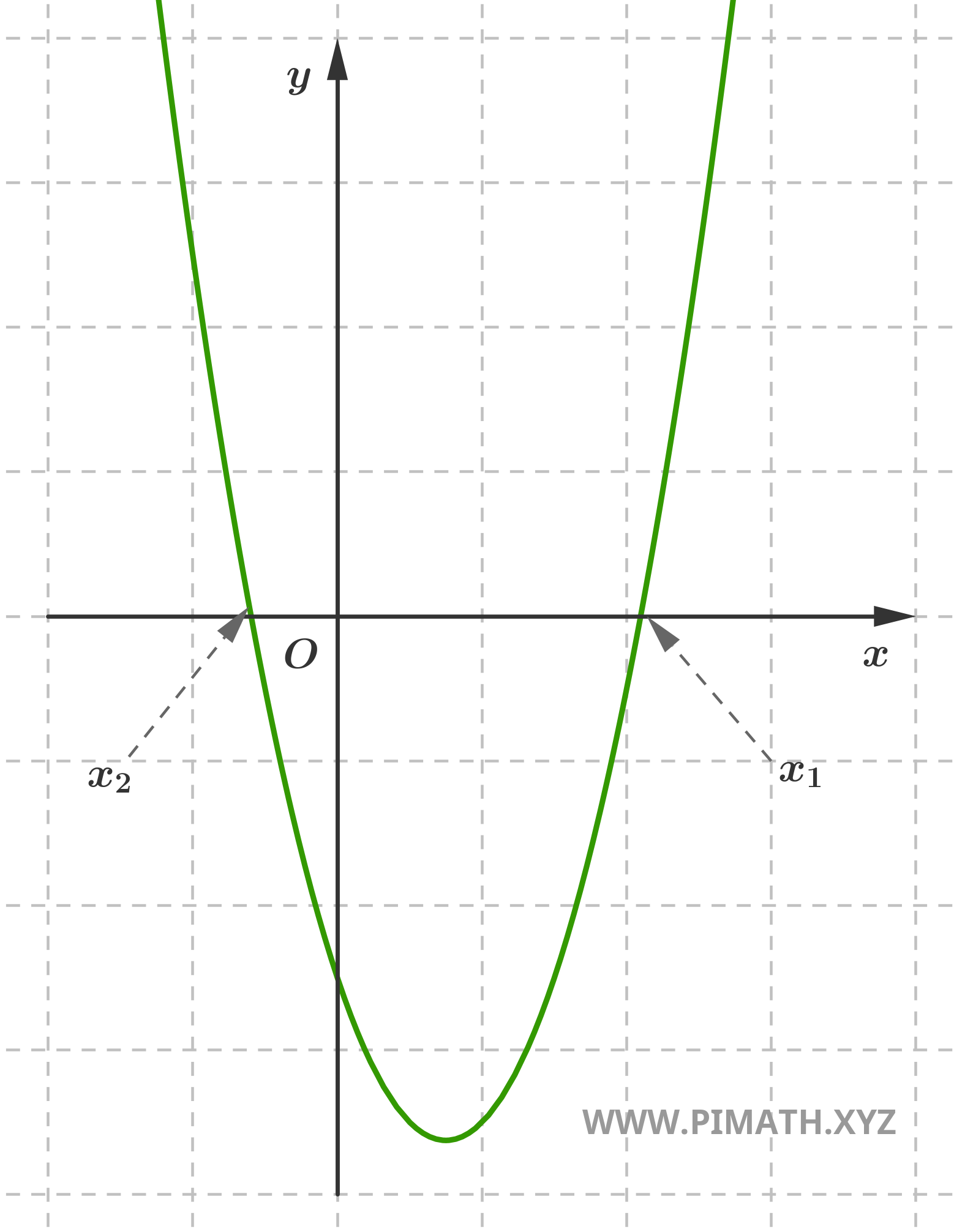
Exercice 2 (forme réduite). Trouver les solutions de l'équation suivante \( x^2 + 6x = 0 \).
Solution. Pour la résoudre, nous pouvons factoriser le facteur commun :
\[ x(x + 6) = 0 \]
Les solutions sont donc : \( x_1 = 0 \) et \( x_2 = -6 \).
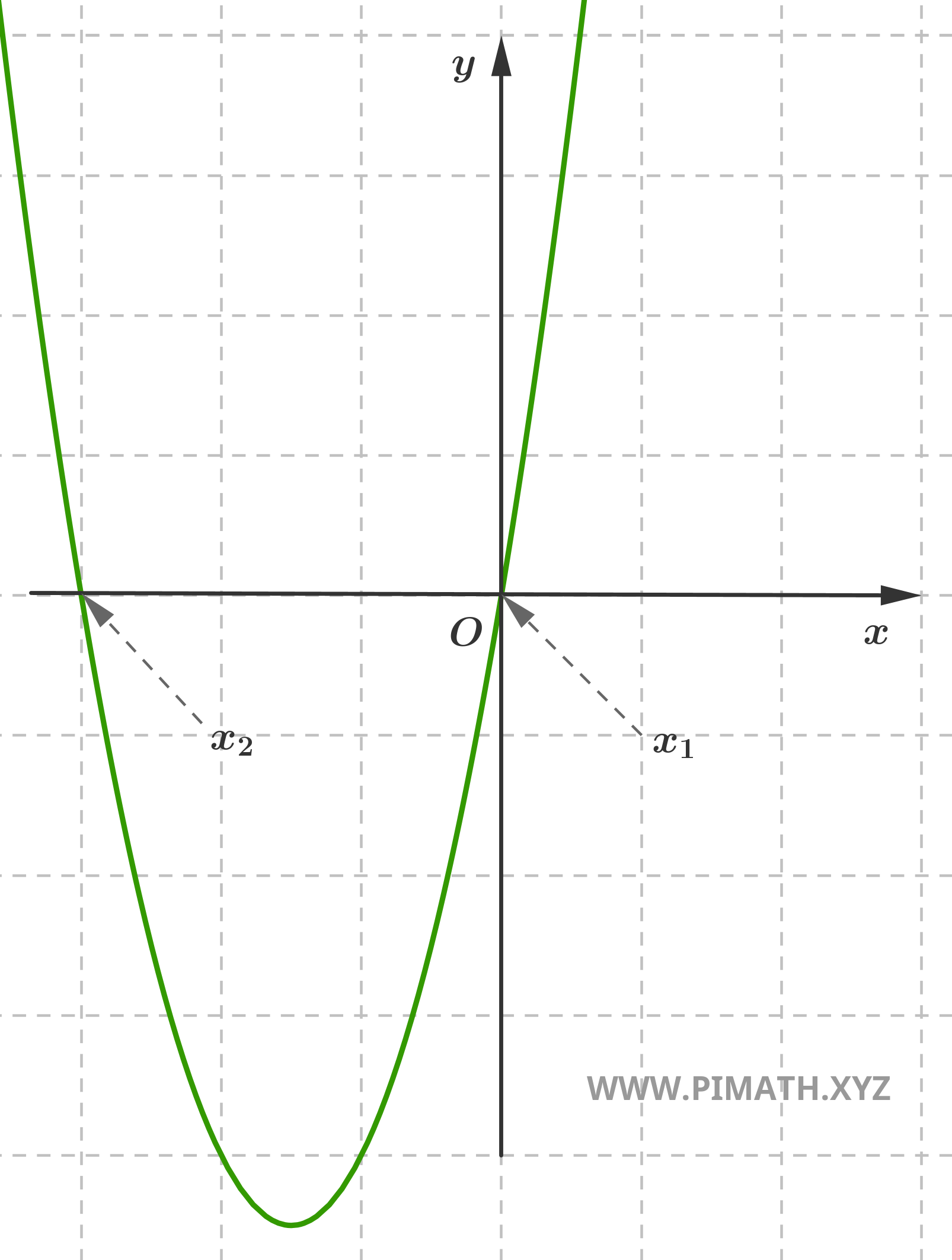
Exercice 3 (équation pure). Trouver les solutions de l'équation \( x^2 = 16 \).
Solution. Pour la résoudre, nous pouvons extraire la racine carrée des deux membres :
\[ x = \pm \sqrt{16} = \pm 4 \]
Les solutions sont donc : \( x_1 = 4 \) et \( x_2 = -4 \).
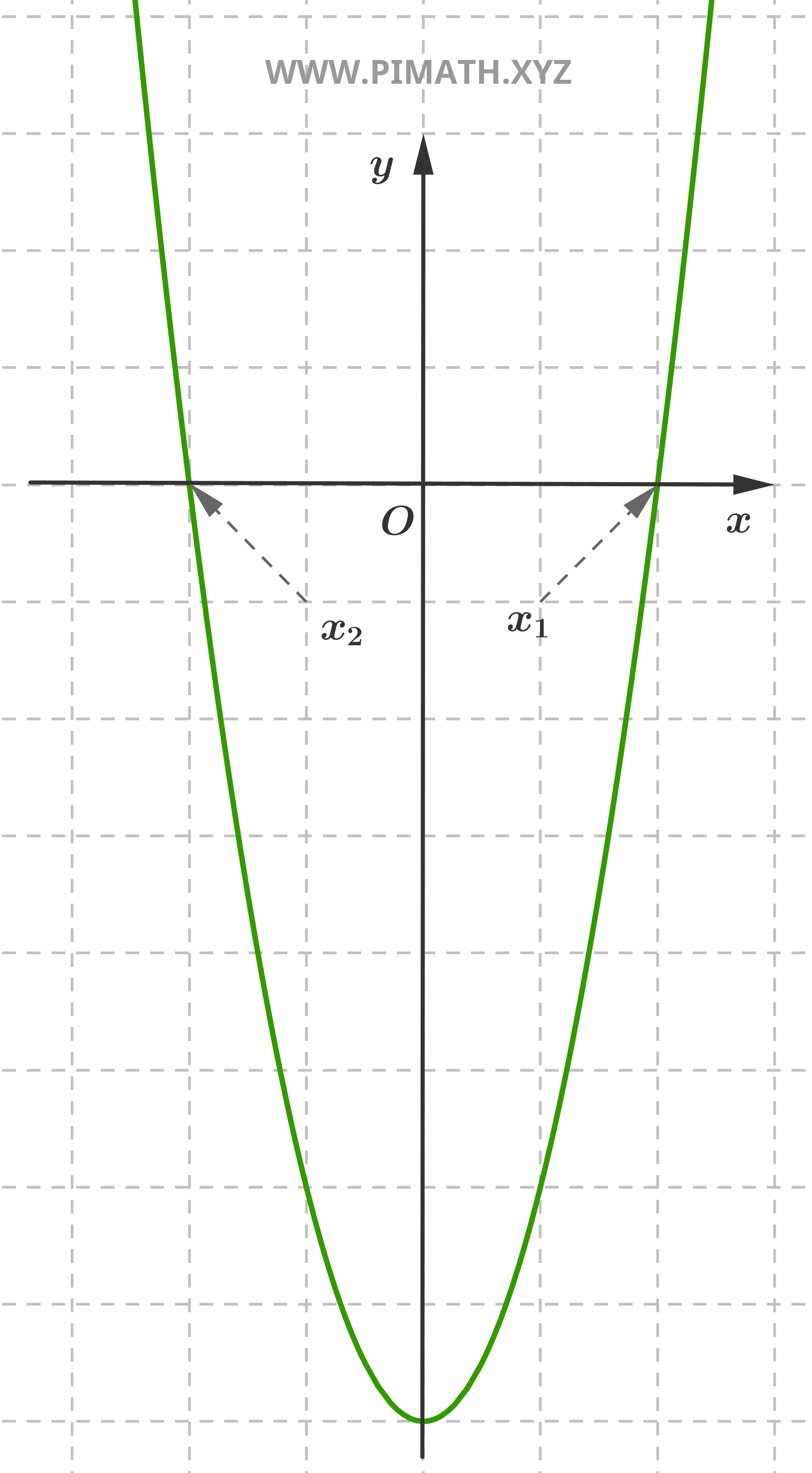
Exercice 4 (équation pure). Trouver les solutions de l'équation \( x^2 + 9 = 0 \).
Solution. Isolons \( x^2 \) :
\[ x^2 = -9 \]
Puisqu'il n'existe pas de nombres réels qui satisfassent cette équation, l'équation n'admet pas de solutions réelles.
Exercice 5. Trouver les solutions de l'équation suivante \( x^2 - 4 = 0 \).
Solution. Isolons \( x^2 \) :
\[ x^2 = 4 \]
Maintenant extrayons la racine carrée des deux membres :
\[ x = \pm \sqrt{4} = \pm 2 \]
Les solutions sont donc :
\[ x_1 = 2 \quad , \quad x_2 = -2 \]
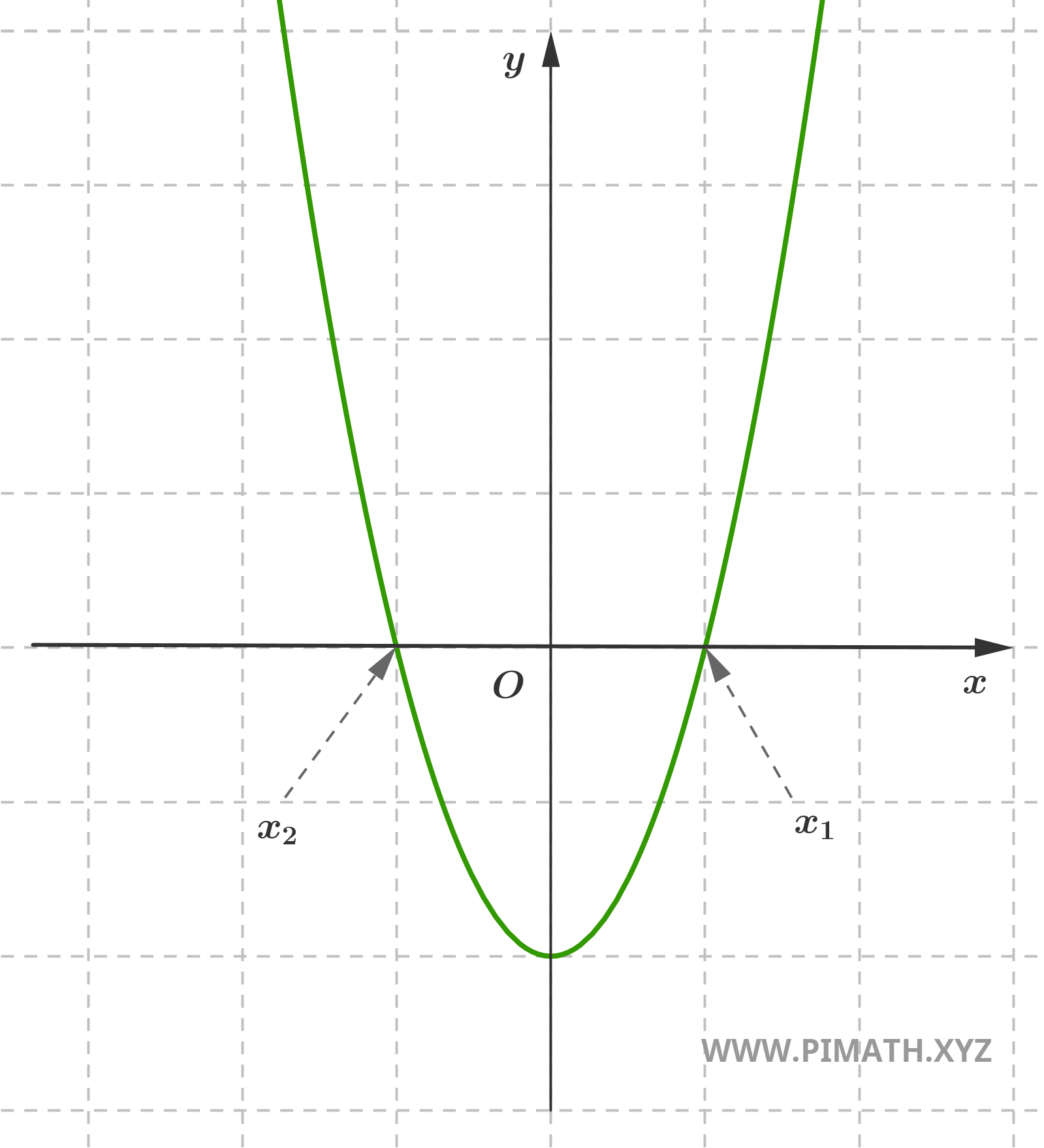
Signification Géométrique
Du point de vue géométrique, résoudre une équation du second degré signifie trouver les valeurs réelles (si elles existent) pour lesquelles la parabole d'équation \( y = ax^2 + bx + c \) coupe l'axe des abscisses \( x \) ou, si l'on préfère, la droite \( y = 0 \).

