Une inéquation du second degré est une expression algébrique qui établit une relation d'ordre entre deux termes contenant une variable du second degré. Elle peut s'écrire sous la forme :
\[ a x^2 + bx + c \leq 0 \quad \text{ou} \quad a x^2 + bx + c \geq 0 \]
où \( a \) et \( b \) sont des coefficients réels avec \( a \neq 0 \) et \( x \) est la variable inconnue. On parle d'inéquation au sens strict si
\[ a x^2 + bx + c < 0 \quad \text{ou} \quad a x^2 + bx + c > 0 \]
- Que sont les Inéquations du Second Degré
- Principes d'Équivalence pour les Inéquations
- Comment résoudre les Inéquations du Second Degré
Que sont les Inéquations du Second Degré
Une inéquation du second degré établit une relation d'ordre entre deux expressions algébriques, et la solution est représentée par un intervalle de valeurs qui vérifient l'inégalité. En d'autres termes, l'ensemble des solutions d'une inéquation du second degré ne sont pas deux valeurs, mais un intervalle ou l'union d'intervalles de nombres réels.
Principes d'Équivalence pour les Inéquations du Second Degré
La résolution d'une inéquation du second degré repose sur deux principes fondamentaux :
Premier Principe d'Équivalence
Le principe d'équivalence pour les inéquations du second degré affirme que si l'on ajoute ou soustrait le même nombre aux deux membres d'une inéquation, la relation d'ordre ne change pas. Par exemple :
Si \( a x^2 + b x + c \leq 0 \), alors nous pouvons ajouter \( d \) aux deux membres et obtenir :
\[ (a x^2 + b x + c) + d \leq 0 + d \]
Deuxième Principe d'Équivalence
Le deuxième principe d'équivalence affirme que si l'on multiplie ou divise les deux membres d'une inéquation par un nombre positif, la relation d'ordre ne change pas. Cependant, si l'on multiplie ou divise par un nombre négatif, l'inéquation doit être inversée. Voici quelques exemples :
Si \( a x^2 + b x + c \leq 0 \) et nous multiplions les deux membres par un nombre positif \( k \), nous obtenons :
\[ k(a x^2 + b x + c) \leq k \cdot 0 \]
Si, en revanche, nous multiplions par un nombre négatif \( k \), l'inéquation devient :
\[ k(a x^2 + b x + c) \geq k \cdot 0 \]
Lorsque l'on multiplie ou divise les deux membres d'une inéquation du second degré par un nombre négatif, il faut inverser le signe de l'inéquation. Par exemple :
Si \( -2 x^2 + 4 x \leq 6 \), en divisant les deux membres par \( -2 \), nous devons inverser le signe de l'inéquation :
\[ x^2 - 2 x \geq -3 \]
Comment résoudre les Inéquations du Second Degré
La première étape consiste à réécrire l'inéquation sous forme canonique, nous portons donc tous les termes au premier membre :
\[ ax^2+bx+c \leq 0 \quad \text{ou} \quad ax^2+bx+c \geq 0 \]
\[ ax^2+bx+c < 0 \quad \text{ou} \quad ax^2+bx+c > 0 \]
selon qu'il s'agisse d'une inégalité ou d'une inégalité au sens strict.
À ce stade, nous devons calculer les racines (ou solutions) de l'équation associée, en utilisant la formule résolutive pour les équations du second degré :
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}, \quad \text{avec} \quad \Delta = b^2 - 4ac \]
Les solutions obtenues nous permettront de déterminer les intervalles dans lesquels l'inéquation est vérifiée, c'est-à-dire les valeurs de \(x\) pour lesquelles l'inéquation est satisfaite, tant à l'intérieur qu'à l'extérieur de ces intervalles.
Le signe du discriminant \( \Delta \) nous permet de comprendre la nature des solutions : si \( \Delta > 0 \), il y a deux solutions réelles distinctes ; si \( \Delta = 0 \), il y a deux solutions réelles et coïncidentes ; si \( \Delta < 0 \), il n'y a pas de solutions réelles.
Résolution de l'inéquation :
Si le coefficient quadratique de l'équation associée est supérieur à zéro, alors les solutions seront :
- \( (x_1, x_2) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c < 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1) \cup (x_2, +\infty) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c > 0 \quad , \quad a > 0 \]
- \( [x_1, x_2] \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c \leq 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c \geq 0 \quad , \quad a > 0 \]
Dans le cas où le coefficient quadratique est négatif (\(a < 0\)), les intervalles de solution seront inversés :
- \( (-\infty, x_1) \cup (x_2, +\infty) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c < 0 \quad , \quad a < 0 \]
- \( (x_1, x_2) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c > 0 \quad , \quad a < 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c \leq 0 \quad , \quad a < 0 \]
- \( [x_1, x_2] \) si l'inéquation que nous voulons étudier est
\[ ax^2+bx+c \geq 0 \quad , \quad a < 0 \]
Comme nous le verrons dans la section dédiée à la représentation graphique, vous n'aurez pas besoin d'apprendre ces règles par cœur.
Exemples Pratiques avec Explications Étape par Étape
Voyons quelques exemples de résolution d'une inéquation du second degré.
Exercice 1. Trouver les valeurs pour lesquelles l'inéquation suivante \( x^2 - 5x \leq -6 \) est vraie.
Solution. Pour résoudre cette inéquation, nous suivons les étapes fondamentales. Tout d'abord, nous portons tout au premier membre afin d'obtenir la forme canonique :
\[ x^2 - 5x + 6 \leq 0 \]
Maintenant nous calculons le discriminant de l'équation associée. En considérant l'expression \( x^2 - 5x + 6 \), nous obtenons :
\[ \Delta = (-5)^2 - 4(1)(6) = 25 - 24 = 1 \]
Le discriminant est positif, donc l'équation a deux solutions réelles distinctes. En résolvant l'équation associée \( x^2 - 5x + 6 = 0 \), nous trouvons les valeurs :
\[ x_{1,2} = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2} \]
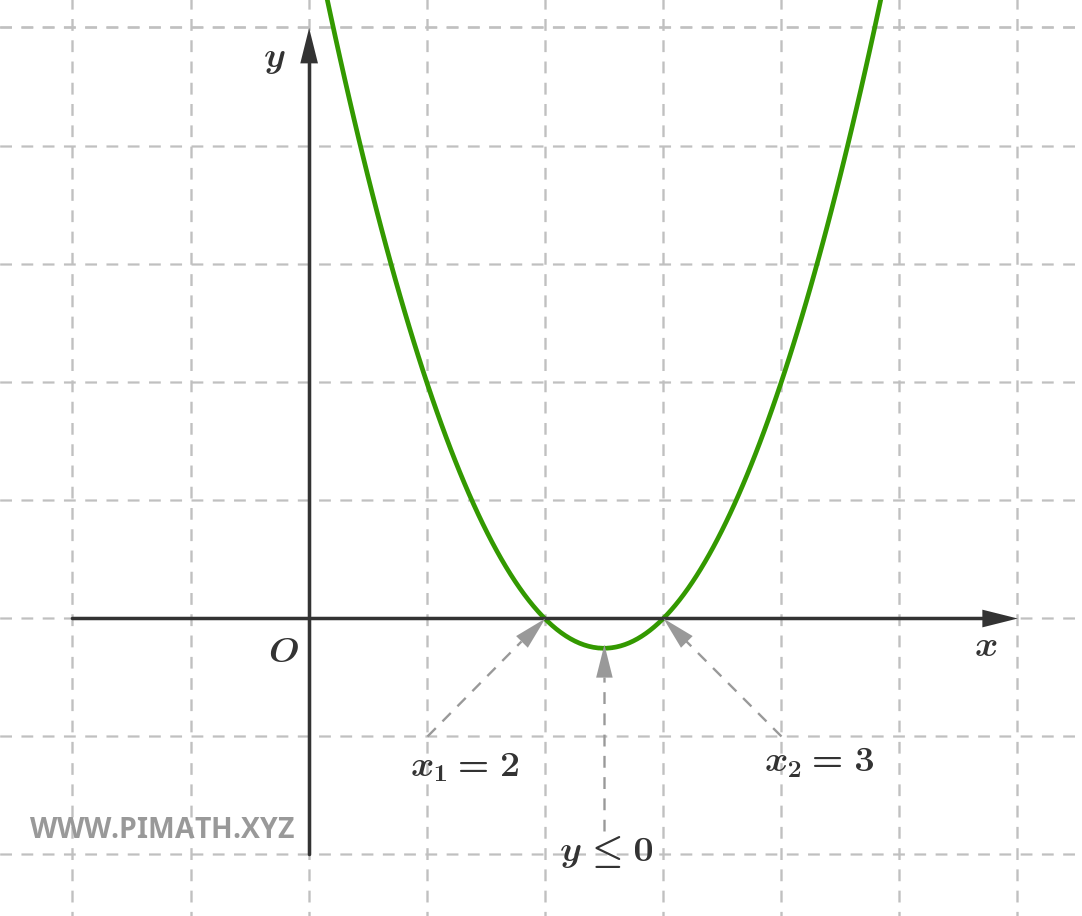
donc \( x_1 = 2 \) et \( x_2 = 3 \).
Puisque le coefficient du terme \( x^2 \) est positif, la parabole a la concavité dirigée vers le haut et l'inéquation sera satisfaite dans l'intervalle compris entre les deux solutions.
Les solutions \( 2 \leq x \leq 3 \) peuvent être représentées graphiquement comme suit :
Habituellement, pour éviter de dessiner chaque fois la parabole, on préfère reporter les solutions sur une droite, en distinguant les valeurs positives par une ligne continue et les négatives par une ligne pointillée. Par exemple, les solutions de l'inéquation précédente sont représentées de cette manière :
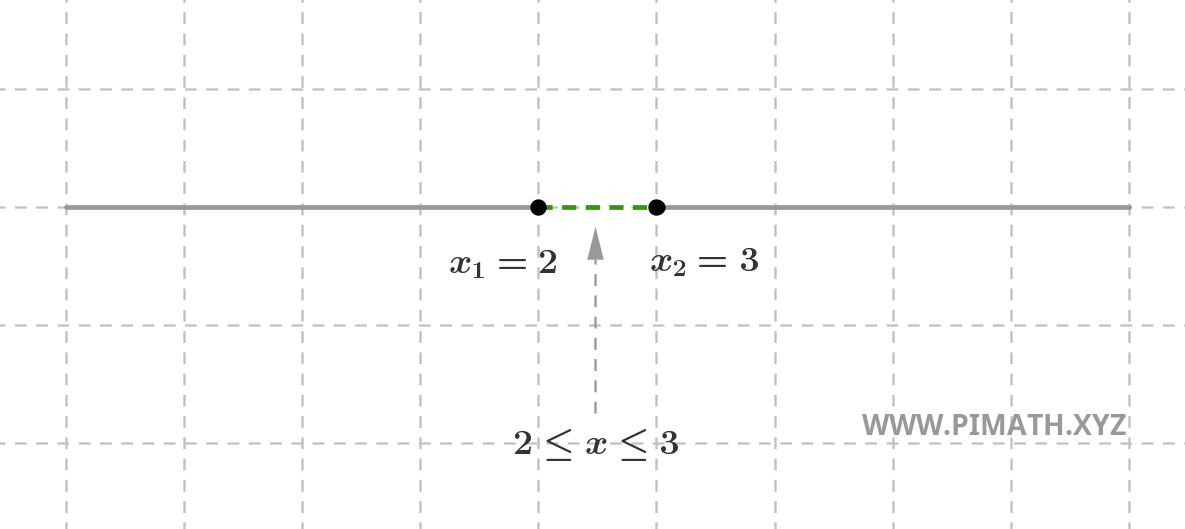
Attention à l'inclusion des solutions : Si nous étudions une inéquation au sens strict (\( < \) ou \( > \)), les racines de l'équation associée doivent être exclues, et cela se représente par des cercles vides dans la représentation graphique. Si en revanche l'inéquation est au sens large (\( \leq \) ou \( \geq \)), les racines sont incluses et sont indiquées par des cercles pleins.
Exercice 2. Résoudre l'inéquation du second degré \( 2x^2 - 4x - 6 > 0 \)
Solution. Nous calculons le discriminant \( \Delta = b^2 - 4ac \)
Pour cette équation, \( a = 2 \), \( b = -4 \), et \( c = -6 \). En substituant ces valeurs dans la formule :
\[ \Delta = (-4)^2 - 4(2)(-6) = 16 + 48 = 64 \]
Puisque \( \Delta > 0 \), l'équation a deux solutions réelles distinctes.
La formule résolutive pour l'équation associée est :
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} \]
En substituant \( b = -4 \), \( \Delta = 64 \), et \( a = 2 \) dans la formule :
\[ x_{1,2} = \frac{4 \pm \sqrt{64}}{2 \times 2} = \frac{4 \pm 8}{4} \]
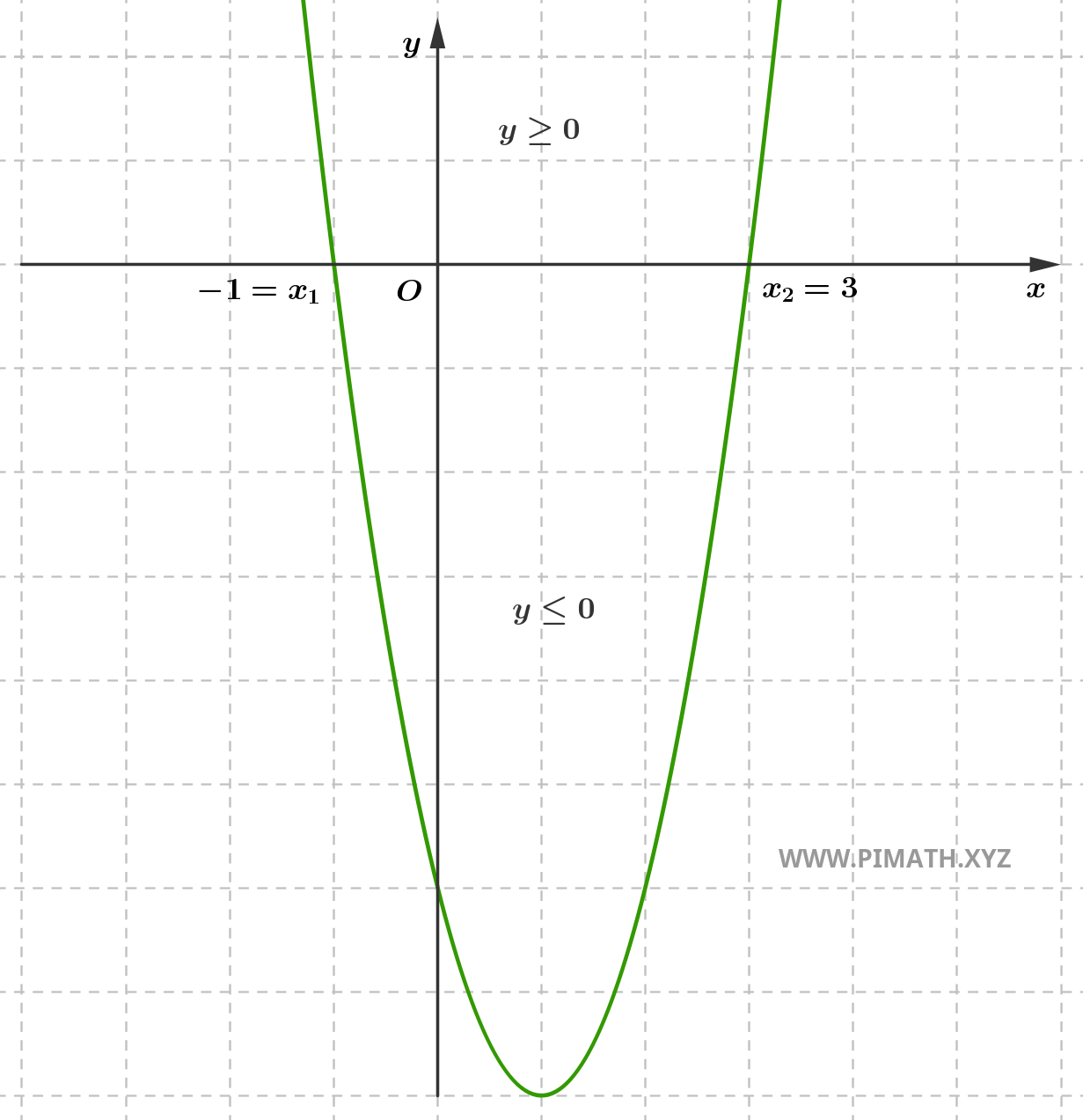
La première solution est \( x_1 = \displaystyle \frac{4 - 8}{4} = \displaystyle \frac{-4}{4} = -1 \), la deuxième solution est en revanche \( x_2 = \displaystyle \frac{4 + 8}{4} = \displaystyle \frac{12}{4} = 3 \).
Les solutions de l'équation sont donc :
\[ x_1 = -1 \quad \text{et} \quad x_2 = 3 \]
Notez que le coefficient quadratique est supérieur à zéro et l'inéquation demande les solutions pour lesquelles on a \( ax^2+bx+c > 0 \), donc les solutions positives se trouvent "externes à l'intervalle", c'est-à-dire \( x < -1 \) ou \( x > 3 \), comme le montre le graphique :
Ou bien :
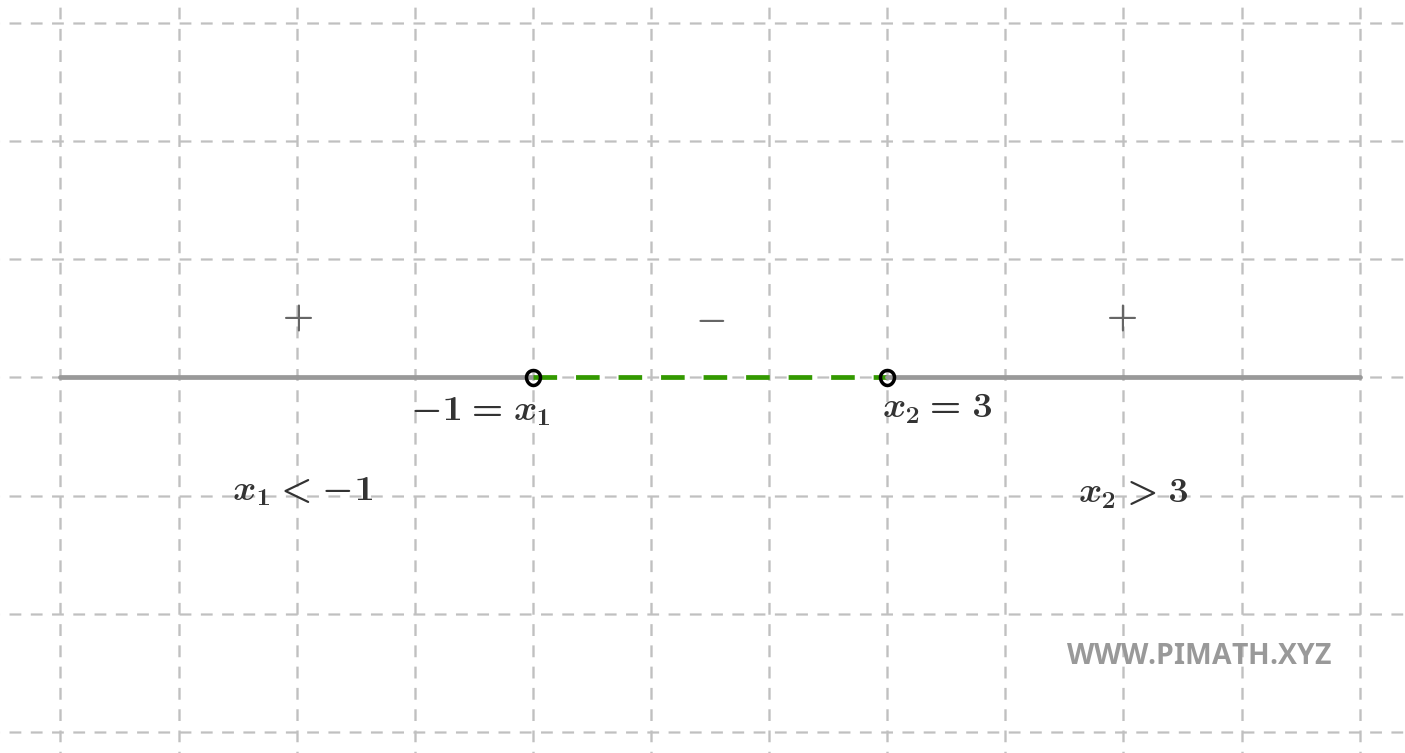
Observez, enfin, que les cercles ne sont pas pleins car nous excluons les points \( x = -1 \) et \( x = 3 \).
Exercice 3. Résoudre l'inéquation du second degré \( 2x^2+x+1 \leq 0 \).
Solution. L'inéquation se présente déjà sous forme canonique.
Nous calculons le discriminant :
\[ \Delta = b^2 - 4ac \]
En substituant \( a = 2 \), \( b = 1 \), \( c = 1 \) :
\[ \Delta = (1)^2 - 4(2)(1) = 1 - 8 = -7 \]
Puisque le discriminant est négatif, l'équation associée \( 2x^2+x+1 = 0 \) n'a pas de solutions réelles.
De plus, puisque le coefficient du terme quadratique est positif (\( a = 2 > 0 \)), la parabole a la concavité dirigée vers le haut, ce qui signifie que sa valeur est toujours positive pour toute valeur de \( x \).
Pour une inéquation de la forme \( 2x^2+x+1 \leq 0 \) avec \( a > 0 \) et discriminant négatif, l'inéquation n'a pas de solutions, puisque la fonction est toujours positive et ne peut jamais être inférieure ou égale à zéro.
Donc, la solution est l'ensemble vide. Le graphique de la fonction est :
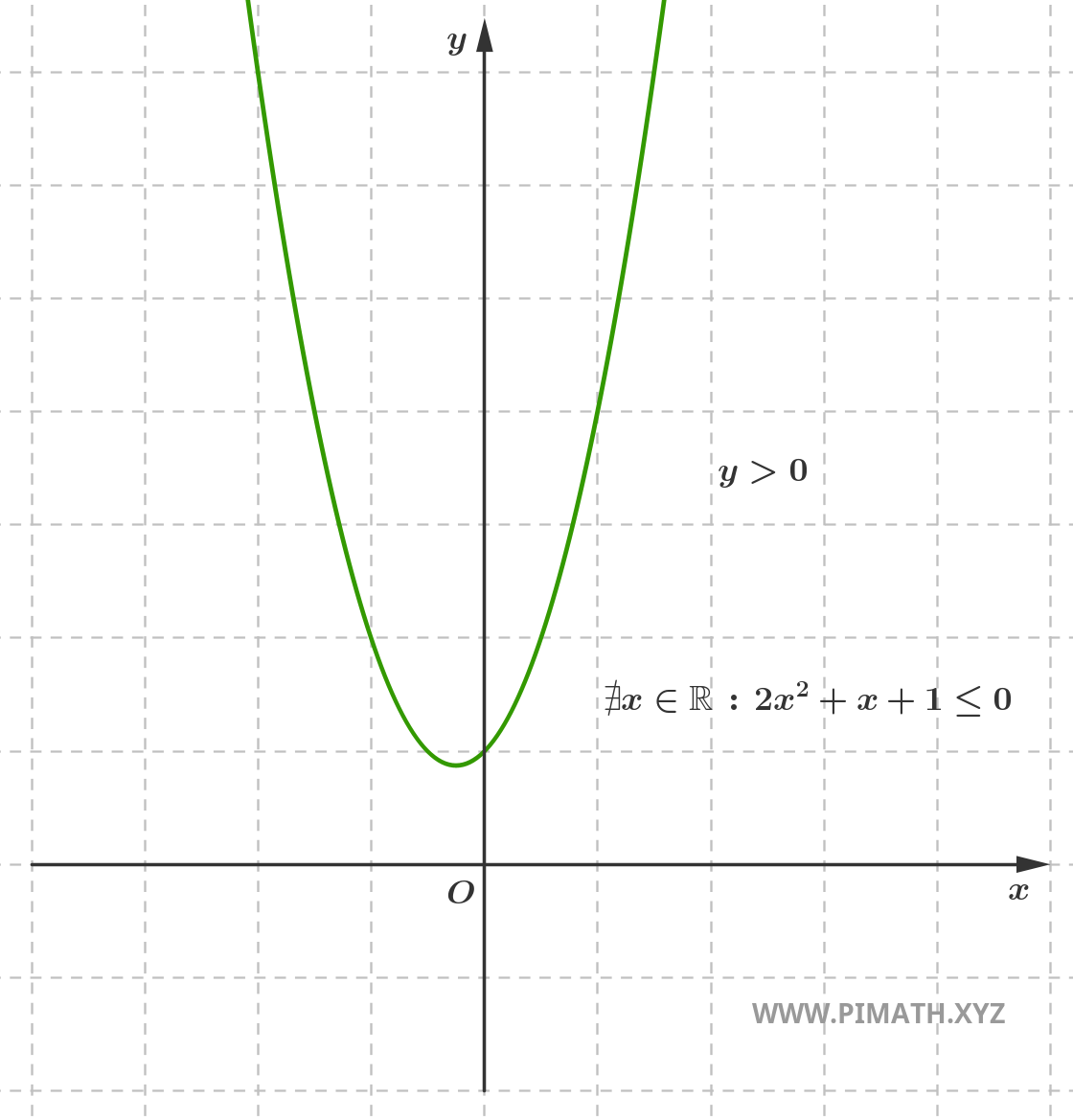
Comme on peut l'observer, la parabole est toujours au-dessus de l'axe \( x \), donc il n'y a pas de valeurs de \( x \) qui satisfont l'inéquation \( 2x^2+x+1 \leq 0 \).

