La droite est un concept primitif de la géométrie euclidienne, c'est-à-dire non définissable en termes plus élémentaires, mais admis comme entité fondamentale. Elle est intuitivement décrite comme l'ensemble infini de points disposés selon une direction constante, s'étendant indéfiniment dans les deux directions. Dans un système de coordonnées cartésiennes, une droite est représentable par une équation linéaire et caractérisée par un coefficient directeur qui détermine son inclinaison par rapport à l'axe des abscisses.
Sommaire
- Comment trouver l'équation de la droite passant par deux points
- Comment trouver l'équation explicite de la droite
- Comment trouver l'équation implicite de la droite
- Signification géométrique du coefficient directeur
- Comment trouver l'équation paramétrique de la droite
- Comment trouver la droite perpendiculaire à une droite donnée
- Exercices résolus sur la droite
Comment trouver l'équation de la droite passant par deux points
Supposons que nous connaissions deux points distincts du plan cartésien : \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \).
L'équation des points appartenant à la droite passant par \( P_1 \) et \( P_2 \) est donnée par la formule suivante :
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
En effet, il suffit d'observer que les triangles \( \triangle P_1P'P \) et \( \triangle P_1P'_2P_2 \) dans la figure :
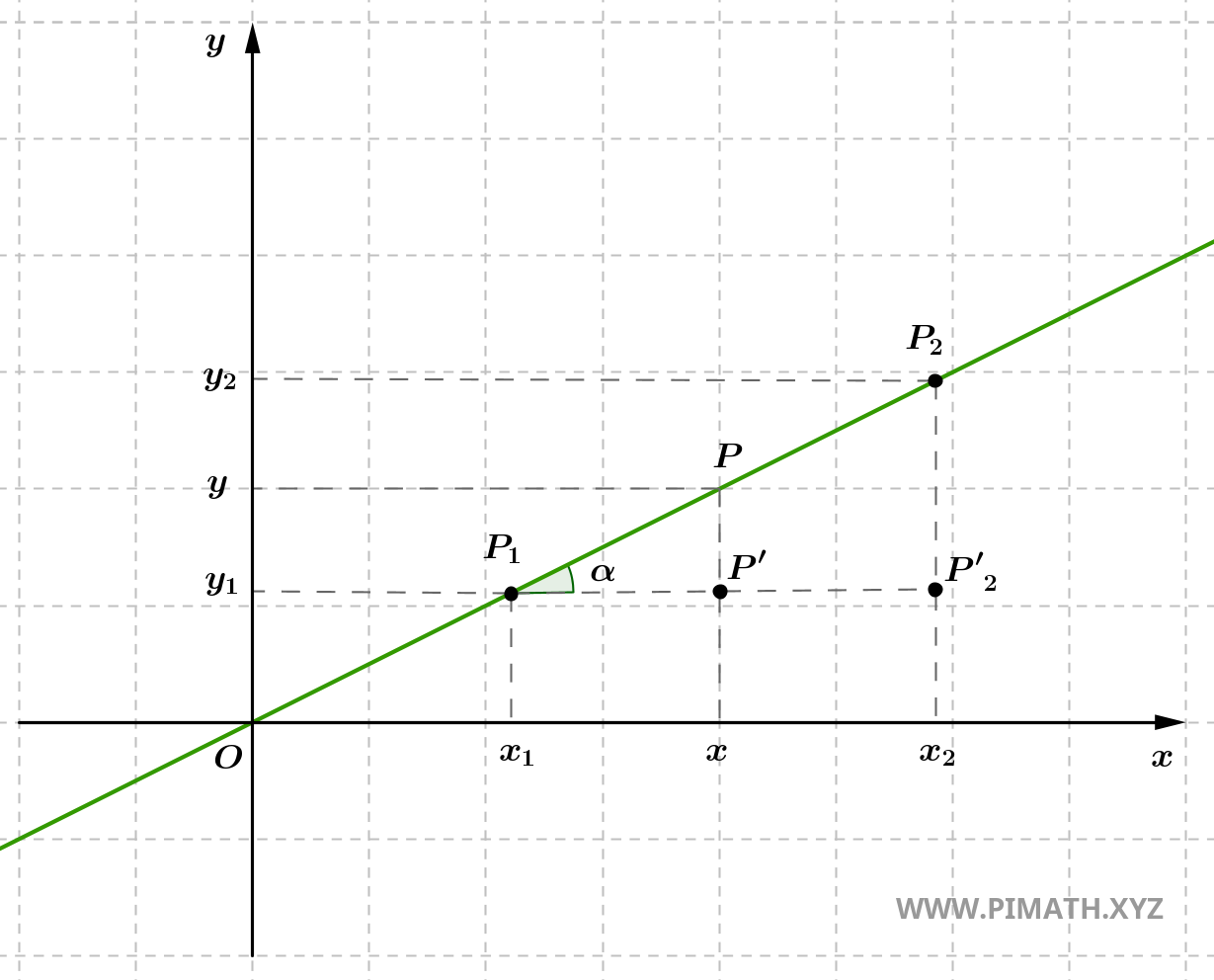
sont semblables selon le premier critère de similitude, lequel affirme que deux triangles sont semblables s'ils ont deux angles respectivement congruents. Dans ce cas, les deux triangles présentent un angle droit et un angle aigu congruent, déterminé par l'inclinaison de la droite par rapport à l'axe x. Il en résulte la proportionnalité entre les côtés correspondants.
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
En résolvant par rapport à \( y \), on obtient la forme explicite de l'équation de la droite :
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \]
L'angle aigu commun aux deux triangles, souvent noté \( \alpha \), représente l'angle d'inclinaison de la droite par rapport à l'axe x. Cet angle joue un rôle fondamental dans la géométrie de la droite, car sa tangente fournit la pente de la droite, c'est-à-dire : \[ m = \tan \alpha = \frac{y_2 - y_1}{x_2 - x_1}. \] Cette relation permet d'interpréter la pente comme une mesure de l'inclinaison angulaire de la droite dans le plan cartésien.
Comment trouver l'équation explicite de la droite
L'équation de la droite passant par deux points distincts \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \) peut être écrite sous forme explicite en utilisant la forme dite point-pente :
\[ y = y_1 + m(x - x_1) \]
où
\[ m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]
est le coefficient directeur de la droite. Cette expression permet de calculer la valeur de \( y \) correspondant à chaque valeur donnée de \( x \), en partant d'un point connu sur la droite et de sa pente.
À partir de cette forme, il est possible d'obtenir la forme explicite canonique de l'équation de la droite, qui est :
\[ y = mx + b \]
Dans cette équation :
- \( m \) est le coefficient directeur, qui représente la pente de la droite ;
- \( b \) est l'ordonnée à l'origine, c'est-à-dire la valeur de \( y \) au point où la droite coupe l'axe des ordonnées (soit quand \( x = 0 \)).
Cette forme est particulièrement utile car elle rend immédiatement évidents à la fois la direction de la droite (par \( m \)) et son point d'intersection avec l'axe y (par \( b \)). Si l'on connaît \( m \) et \( b \), il est possible de tracer la droite sans avoir besoin d'autres points.
Pour passer de la forme point-pente à la forme canonique, il suffit de développer les calculs et d'isoler \( y \). Par exemple :
\[ y = y_1 + m(x - x_1) = mx + (y_1 - mx_1) \]
D'où l'on obtient directement :
\[ y = mx + b \quad \text{avec} \quad b = y_1 - mx_1 \]
Comment trouver l'équation implicite de la droite
Partons de la forme point-pente de l'équation de la droite, qui passe par deux points \( (x_1, y_1) \) et \( (x_2, y_2) \) :
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
Nous multiplions les deux membres par \( x_2 - x_1 \neq 0 \) :
\[ (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1) \]
Nous développons les deux membres :
\[ (x_2 - x_1)y - (x_2 - x_1)y_1 = (y_2 - y_1)x - (y_2 - y_1)x_1 \]
Nous faisons passer tous les termes au premier membre :
\[ (x_2 - x_1)y - (y_2 - y_1)x + \left( (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \right) = 0 \]
Voici la forme implicite de l'équation de la droite. Si nous définissons les coefficients comme :
\[ \begin{cases} a = -(y_2 - y_1) \\ b = x_2 - x_1 \\ c = (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \end{cases} \]
l'équation prend la forme générale :
\[ ax + by + c = 0 \]
Alternativement, si nous introduisons la pente \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \), nous pouvons partir de la forme explicite de la droite :
\[ y = m(x - x_1) + y_1 \]
Nous faisons passer tout au premier membre pour obtenir la forme implicite :
\[ y - m x + (m x_1 - y_1) = 0 \]
Donc la forme implicite avec pente \( m \) est :
\[ a = -m, \quad b = 1, \quad c = m x_1 - y_1 \]
et la forme générale :
\[ ax + by + c = 0 \]
La forme implicite est utile lorsque l'on veut étudier les propriétés géométriques de la droite ou vérifier l'appartenance d'un point sans avoir à résoudre pour \( y \).
Signification géométrique du coefficient directeur
Dans le contexte de cette équation, le terme :
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
représente la pente de la droite, c'est-à-dire le coefficient directeur. La pente est une mesure de l'inclinaison de la droite par rapport à l'axe des abscisses (l'axe x). Si la pente est positive, la droite est croissante (monte de gauche à droite) ; si elle est négative, la droite est décroissante (descend de gauche à droite).
En d'autres termes, la pente décrit la vitesse à laquelle la droite croît ou décroît par rapport à l'axe des abscisses x. La pente est un paramètre crucial pour déterminer l'orientation de la droite dans le plan cartésien. Selon la valeur de la pente, nous pouvons faire les observations suivantes :
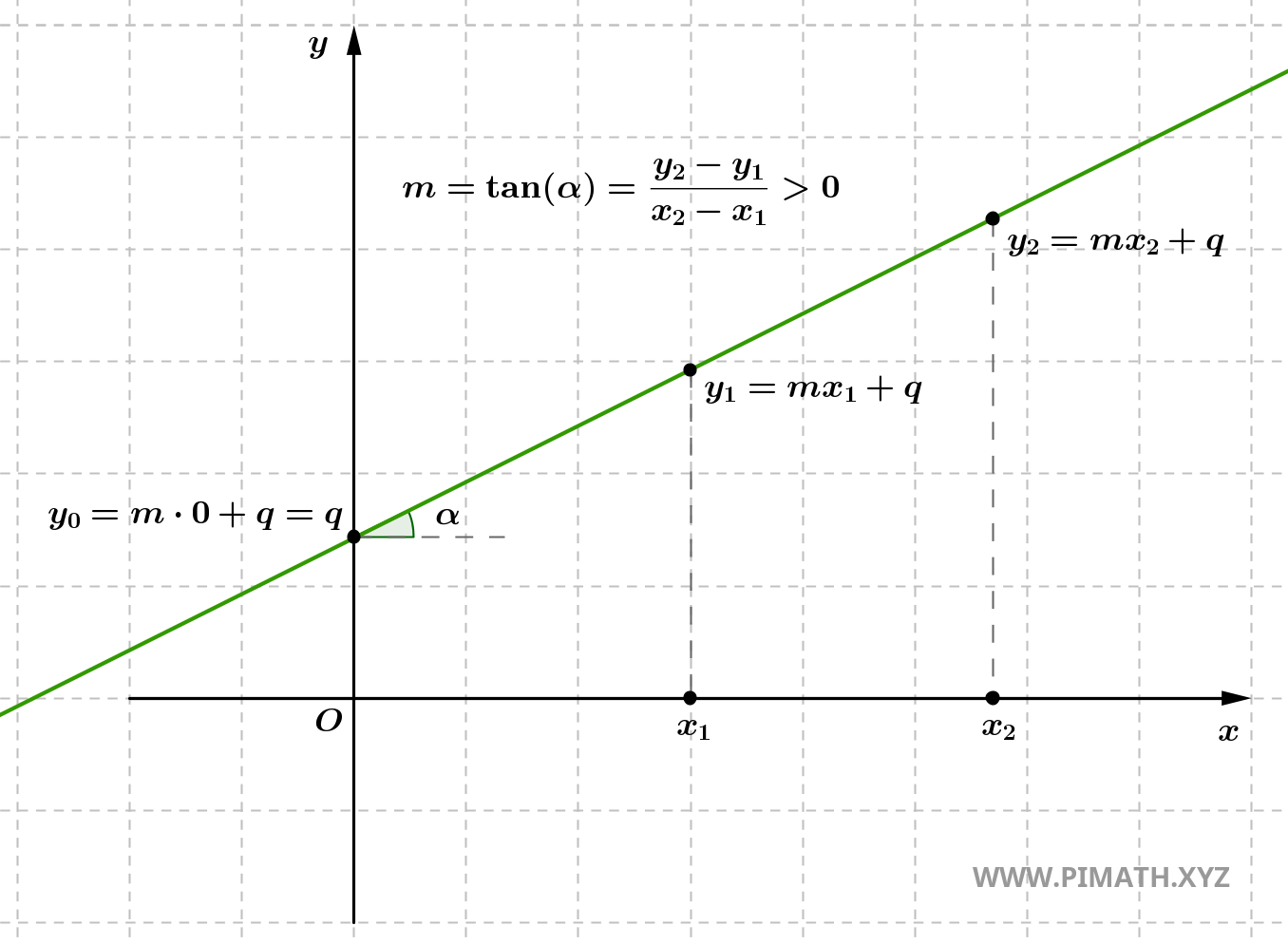
- Si \( m > 0 \), la droite est croissante, c'est-à-dire qu'elle monte de gauche à droite. Cela signifie que pour chaque accroissement de \( x \), \( y \) augmente également. La droite forme un angle aigu avec l'axe x.
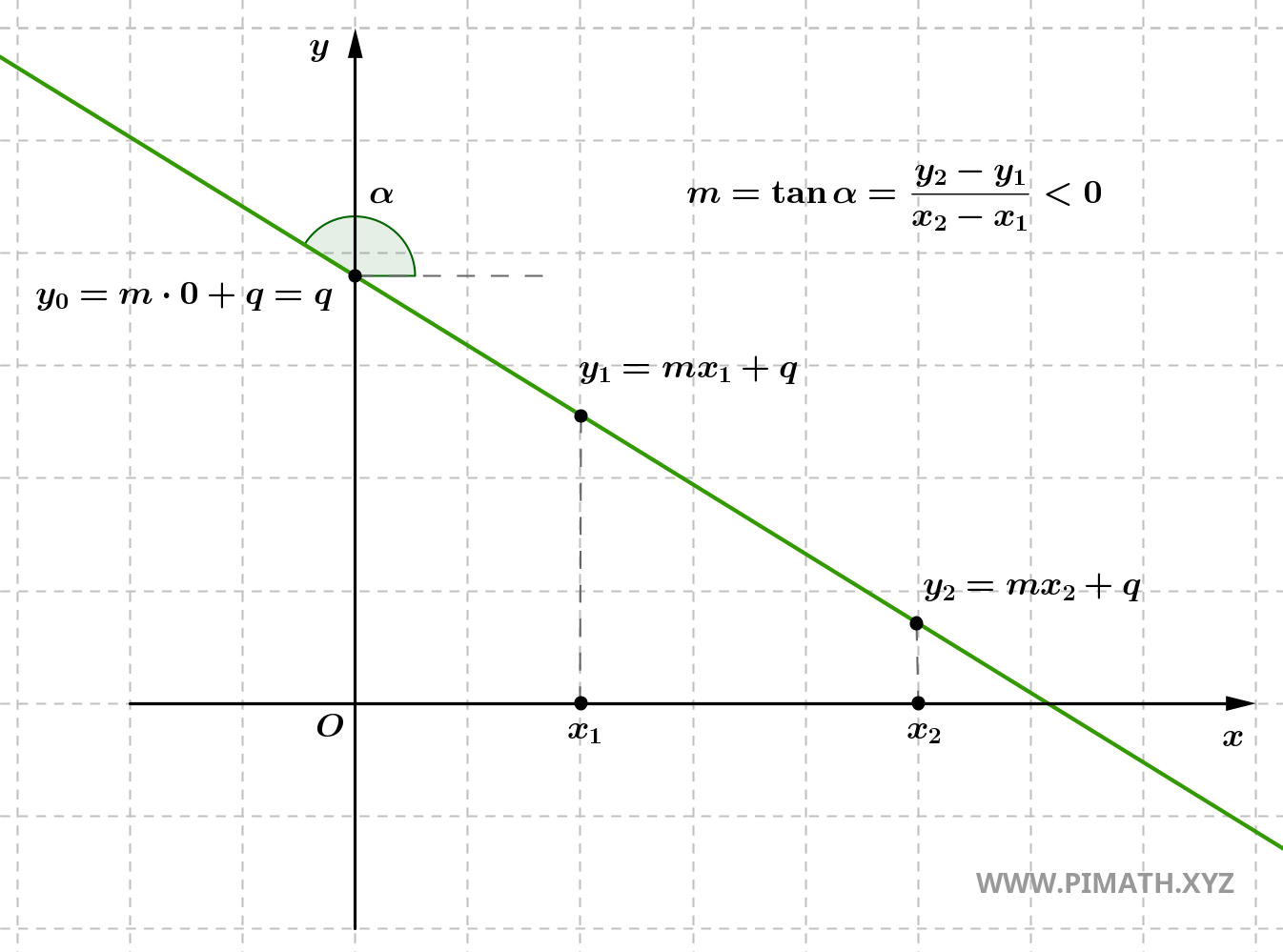
- Si \( m < 0 \), la droite est décroissante, c'est-à-dire qu'elle descend de gauche à droite. Dans ce cas, pour chaque accroissement de \( x \), la valeur de \( y \) diminue. La droite forme un angle obtus avec l'axe x.
- Si \( y_2 = y_1 \), la pente est nulle, ce qui implique que la droite est horizontale. Dans ce cas, il n'y a aucun changement vertical (la différence entre les ordonnées \( y_2 - y_1 \) est nulle). La droite est parallèle à l'axe x et n'a aucune inclinaison verticale.
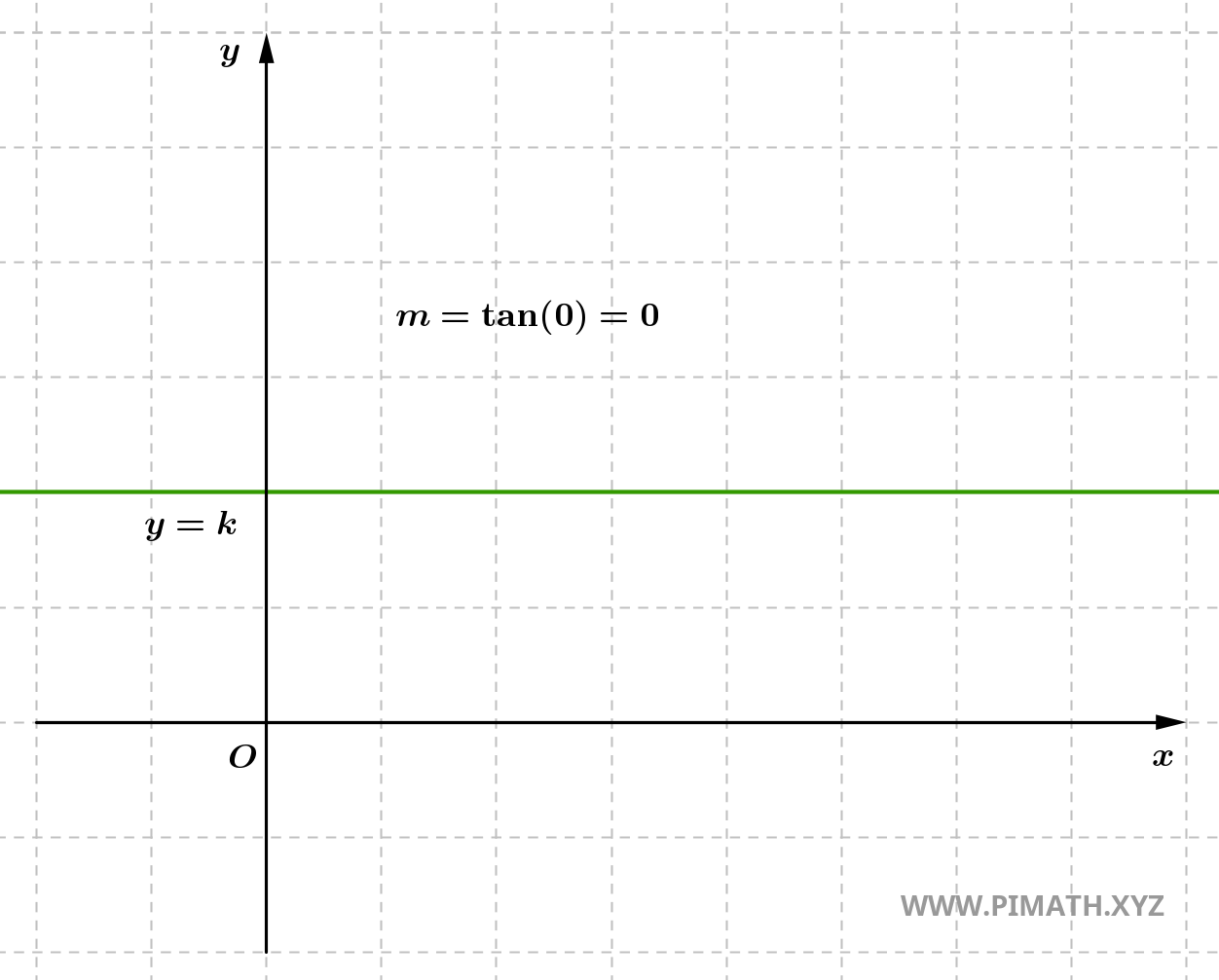
- Si \( x_2 = x_1 \), la pente est indéfinie, ce qui implique que la droite est verticale. Dans ce cas, il n'y a aucun changement horizontal (la différence entre les abscisses \( x_2 - x_1 \) est nulle), donc on ne peut pas définir une pente numérique. La droite est parallèle à l'axe y et n'a aucune inclinaison horizontale.
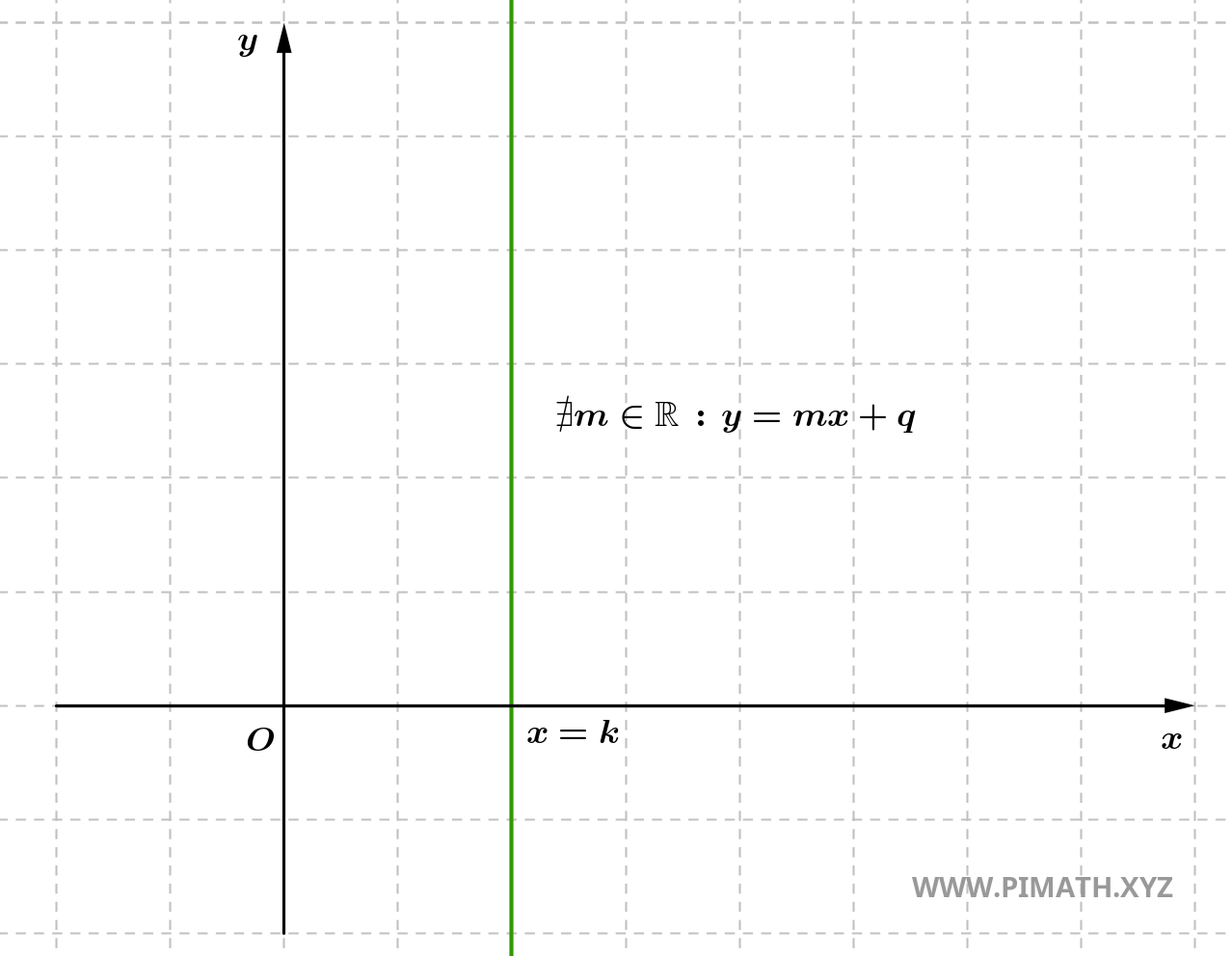
En général, la pente \( m \) nous fournit des informations importantes sur le comportement de la droite. Si la droite est croissante, la valeur de \( y \) augmente lorsque \( x \) augmente ; si elle est décroissante, la valeur de \( y \) diminue lorsque \( x \) augmente ; si la droite est verticale, cela signifie que \( y \) ne dépend pas de \( x \) et la droite n'a aucune inclinaison horizontale.
Comment trouver l'équation paramétrique de la droite
La droite passant par les points \( P_1(x_1, y_1) \) et \( P_2(x_2, y_2) \) peut aussi être décrite sous forme paramétrique. Dans cette représentation, les coordonnées \( x \) et \( y \) d'un point sur la droite sont exprimées en fonction d'un paramètre réel \( t \), qui varie le long de la droite.
L'équation paramétrique de la droite est donnée par :
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Ici, \( t \) est le paramètre qui peut prendre n'importe quelle valeur réelle. Quand \( t \) varie, le point \( (x, y) \) se déplacera le long de la droite qui relie les deux points \( P_1 \) et \( P_2 \).
La forme paramétrique représente donc une famille de points sur la droite, dans laquelle le paramètre \( t \) définit de manière univoque chaque point de la droite. Quand \( t = 0 \), on obtient le point \( P_1(x_1, y_1) \) ; quand \( t = 1 \), on obtient le point \( P_2(x_2, y_2) \). Les valeurs de \( t \) entre 0 et 1 décrivent les points de la droite entre \( P_1 \) et \( P_2 \), tandis que les valeurs de \( t \) supérieures à 1 ou inférieures à 0 étendent la droite au-delà de ces points.
La formule paramétrique se base sur le concept de vecteur directeur, qui est le vecteur reliant \( P_1 \) et \( P_2 \). En effet, la différence \( (x_2 - x_1, y_2 - y_1) \) est le vecteur directeur de la droite, et le paramètre \( t \) est le facteur d'échelle qui permet de se déplacer le long de la droite.
La forme paramétrique est particulièrement utile dans divers domaines de la géométrie analytique, comme dans l'étude des courbes en général.
Comment trouver la droite perpendiculaire à une droite donnée
Quand deux droites sont perpendiculaires, leur pente est liée par une relation bien précise. Si une droite a pour pente \( m \), la pente de la droite perpendiculaire à celle-ci est donnée par :
\[ m_\perp = -\frac{1}{m}. \]
Cette formule exprime le fait que le produit des pentes de deux droites perpendiculaires est égal à \(-1\). La raison de cette relation peut être comprise par le fait que les angles formés par les deux droites doivent être de 90° (un angle droit), et donc la tangente de l'angle entre les droites doit satisfaire cette condition.
Pour trouver l'équation de la droite perpendiculaire passant par un point \( (x_1, y_1) \), nous pouvons utiliser la forme point-pente. La pente de la droite perpendiculaire est \( -\displaystyle \frac{1}{m} \), donc l'équation de la droite perpendiculaire sera :
\[ y - y_1 = -\frac{1}{m} (x - x_1). \]
Dans cette équation, \( (x_1, y_1) \) est le point par lequel passe la droite perpendiculaire, tandis que \( m \) est la pente de la droite originale. La formule décrit une droite qui a la pente opposée et inverse par rapport à la droite originale.
Si la droite originale est représentée par l'équation \( y = mx + b \), la droite perpendiculaire aura pour pente \( m_\perp = -\displaystyle \frac{1}{m} \) et sera écrite sous la forme \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), où \( (x_1, y_1) \) est le point d'intersection entre la droite originale et la droite perpendiculaire.
Cette propriété des droites perpendiculaires est fondamentale dans de nombreux domaines de la géométrie, de la trigonométrie et de la physique, en particulier lors de l'étude d'angles et de trajectoires perpendiculaires entre eux.
Exercices résolus sur la droite
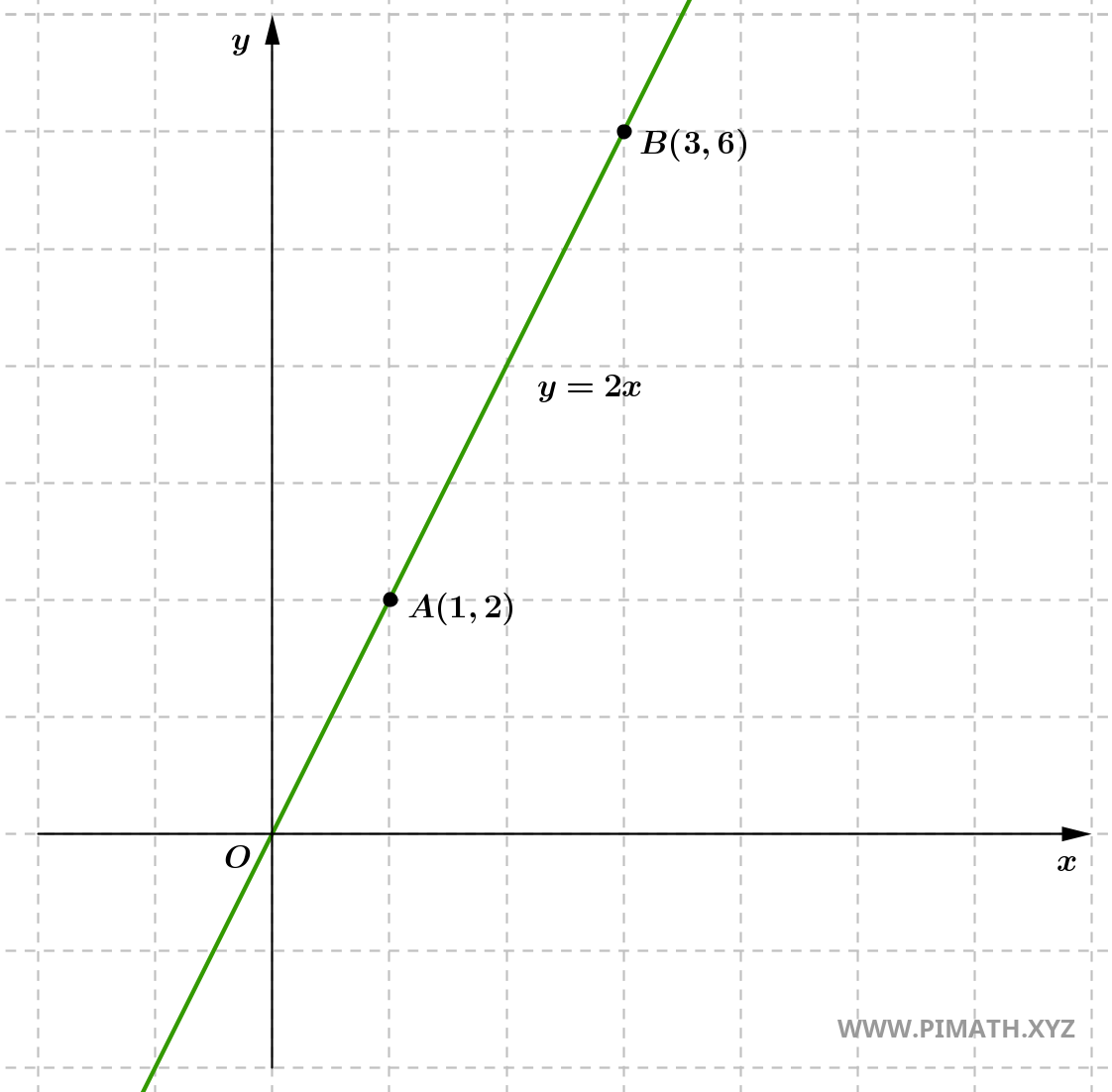
Exercice 1 : Déterminer l'équation explicite de la droite passant par \( A(1, 2) \) et \( B(3, 6) \).
Solution. Nous calculons le coefficient directeur de la droite :
\[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- Nous utilisons l'équation point-pente pour déterminer l'équation de la droite passant par \( A(1, 2) \) et de coefficient directeur \( m = 2 \) : \[ y - 2 = 2(x - 1). \]
- En développant l'équation : \[ y - 2 = 2x - 2. \]
- En simplifiant : \[ y = 2x - 2 + 2 = 2x. \]
Donc, l'équation de la droite passant par les points \( A(1, 2) \) et \( B(3, 6) \) est \[ y = 2x. \]
Vérification : Nous pouvons vérifier que les deux points satisfont cette équation :
- Pour \( A(1, 2) \) : \[ 2 = 2 \cdot 1 = 2 \]
- Pour \( B(3, 6) \) : \[ 6 = 2 \cdot 3 = 6 \]
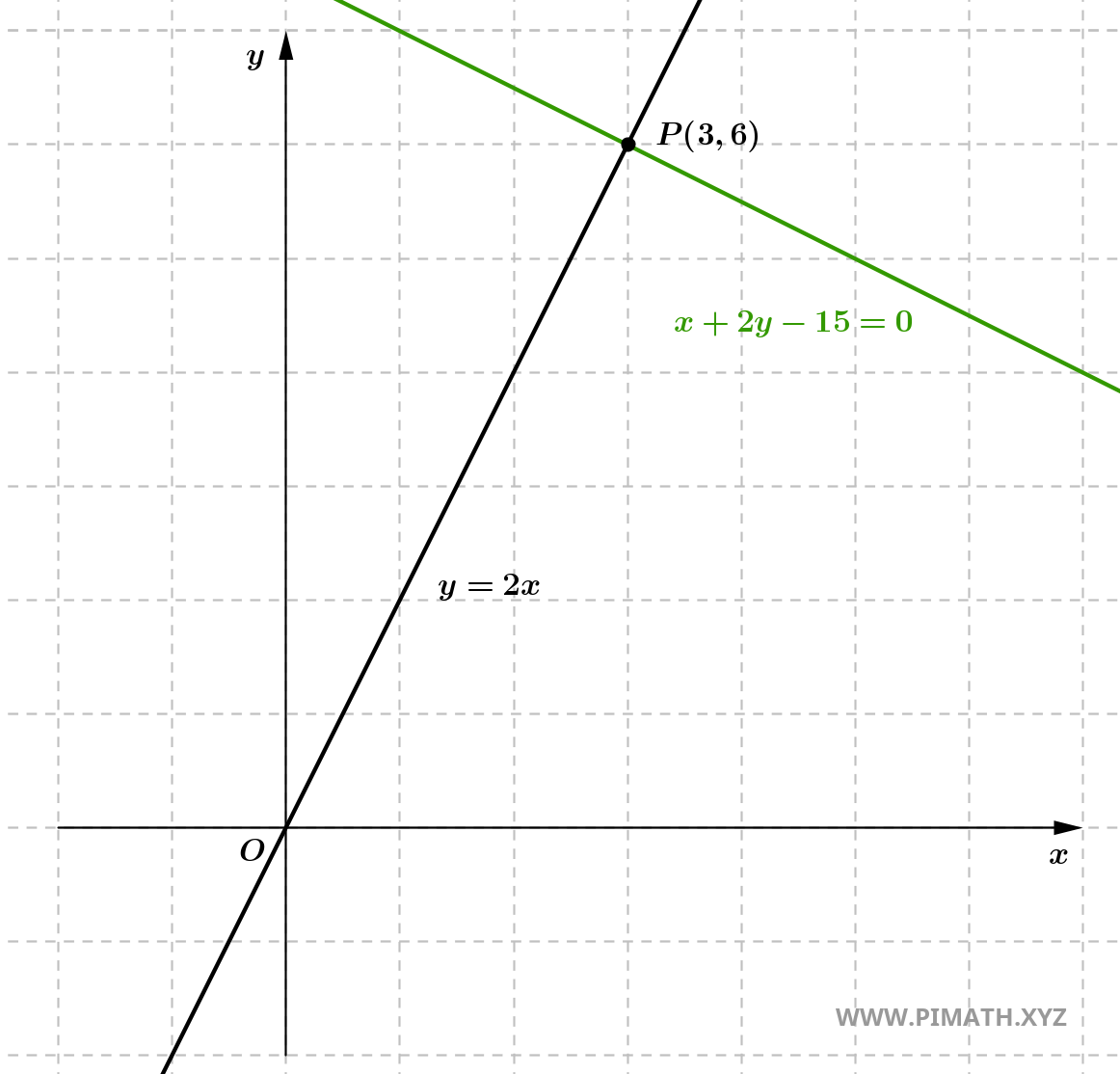
Exercice 2 : Déterminer l'équation de la droite perpendiculaire à la droite \( y = 2x \) et passant par le point \( P(3, 6) \).
Solution. La droite donnée a pour coefficient directeur \( m = 2 \). Le coefficient directeur de la droite perpendiculaire sera :
\[ m_{\perp} = -\frac{1}{2}. \]
- Nous utilisons l'équation point-pente pour déterminer l'équation de la droite passant par \( P(3, 6) \) et de coefficient directeur \( m_{\perp} = -\frac{1}{2} \) : \[ y - 6 = -\frac{1}{2}(x - 3). \]
- Nous développons l'équation : \[ y - 6 = -\frac{1}{2}x + \frac{3}{2}. \]
- Nous faisons passer le terme constant à droite : \[ y = -\frac{1}{2}x + \frac{3}{2} + 6 = -\frac{1}{2}x + \frac{15}{2}. \]
Donc, l'équation de la droite cherchée est : \[ y = -\frac{1}{2}x + \frac{15}{2}. \]
Forme implicite : Nous multiplions les deux membres par 2 :
\[ 2y = -x + 15 \quad \Rightarrow \quad x + 2y - 15 = 0. \]
Vérification : En substituant les coordonnées de \( P(3, 6) \) dans l'équation explicite :
- \[ y = -\frac{1}{2}x + \frac{15}{2} \quad \Rightarrow \quad 6 = -\frac{1}{2} \cdot 3 + \frac{15}{2} = -\frac{3}{2} + \frac{15}{2} = \frac{12}{2} = 6. \]
Le point appartient à la droite, donc la solution est correcte.
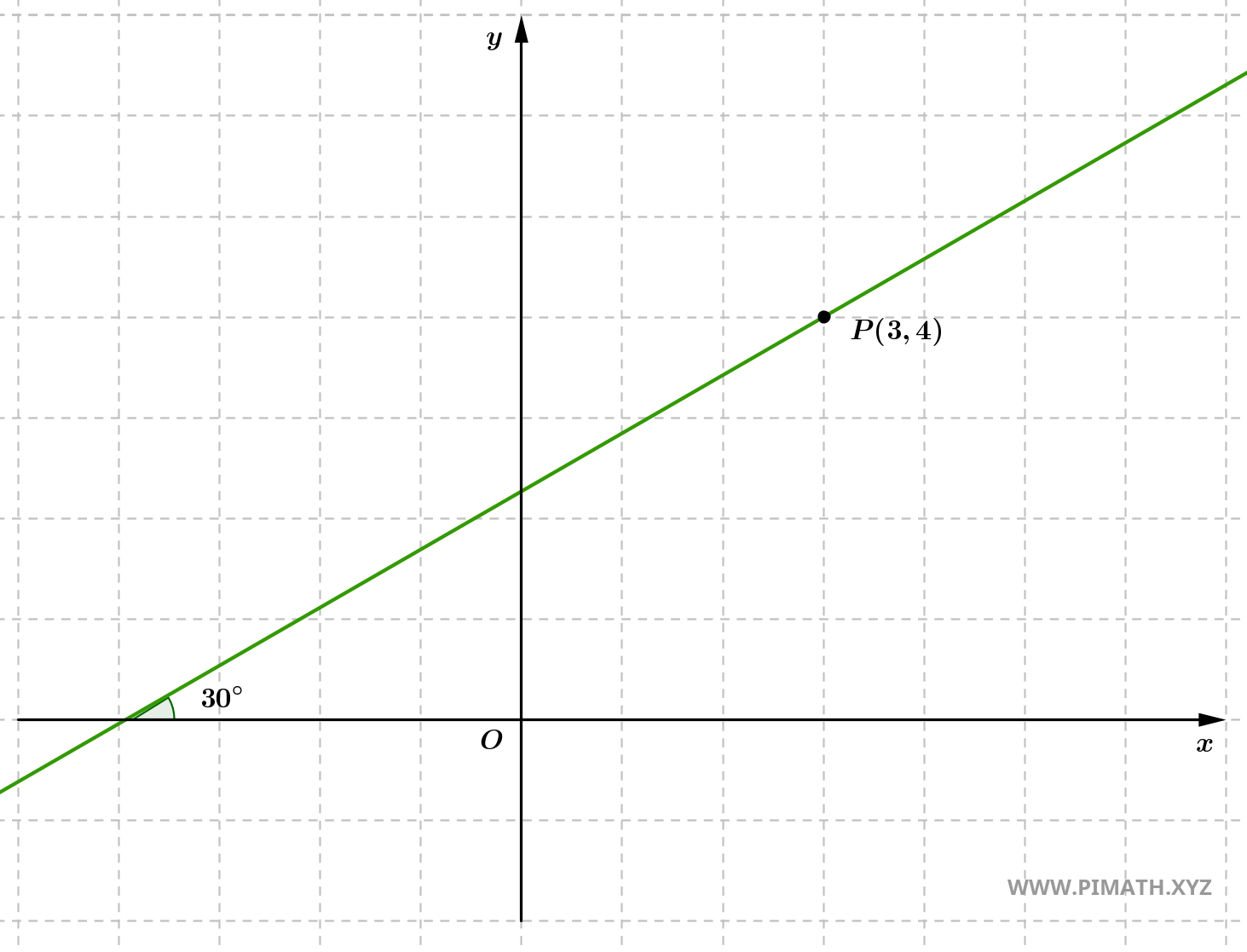
Exercice 3 : Déterminer l'équation de la droite passant par le point \( P(3, 4) \) et formant un angle de \( 30^\circ \) avec l'axe des abscisses.
Solution. L'angle qu'une droite forme avec l'axe des abscisses est lié au coefficient directeur par la tangente :
\[ m = \tan(30^\circ) = \tan\left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}}. \]
- Nous utilisons l'équation point-pente avec le point \( P(3, 4) \) et le coefficient directeur \( m = \frac{1}{\sqrt{3}} \) : \[ y - 4 = \frac{1}{\sqrt{3}}(x - 3). \]
- En développant l'équation : \[ y - 4 = \frac{1}{\sqrt{3}}x - \frac{3}{\sqrt{3}} = \frac{1}{\sqrt{3}}x - \sqrt{3}. \]
- Nous ajoutons 4 aux deux membres : \[ y = \frac{1}{\sqrt{3}}x - \sqrt{3} + 4. \]
- En simplifiant le terme constant : \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Donc, l'équation de la droite cherchée est : \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Vérification : En substituant \( x = 3 \), nous obtenons : \[ y = \frac{1}{\sqrt{3}} \cdot 3 + (4 - \sqrt{3}) = \sqrt{3} + 4 - \sqrt{3} = 4. \]
- Le point \( P(3, 4) \) appartient à la droite, donc la solution est correcte.
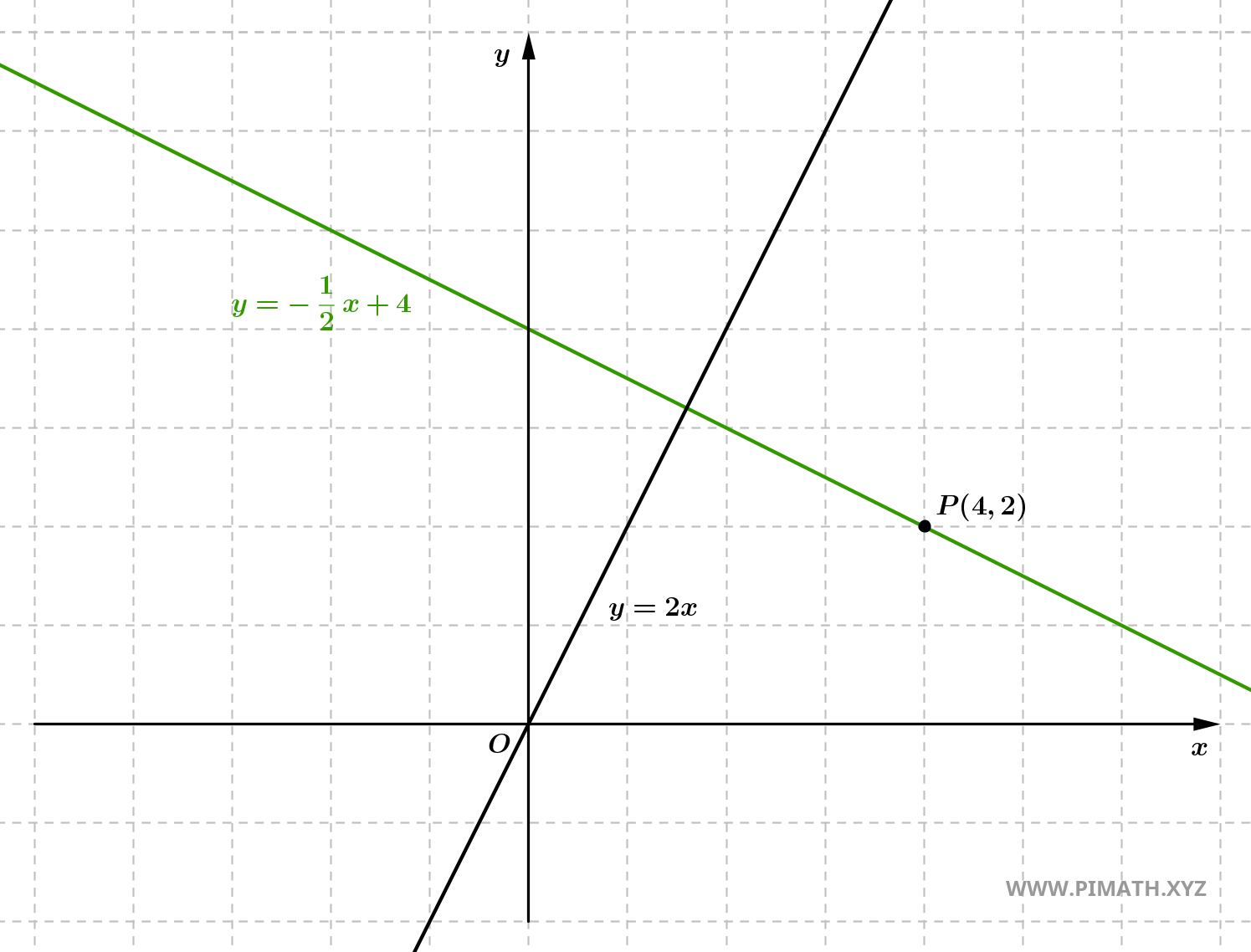
Exercice 4 : Déterminer l'équation de la droite perpendiculaire à la droite \( y = 2x \) et passant par le point \( P(4, 2) \).
Solution. La droite donnée a pour coefficient directeur \( m = 2 \). Le coefficient directeur de la droite perpendiculaire sera :
\[ m_{\perp} = -\frac{1}{2}. \]
- Nous utilisons l'équation point-pente pour déterminer l'équation de la droite passant par \( P(4, 2) \) et de coefficient directeur \( m_{\perp} = -\frac{1}{2} \) : \[ y - 2 = -\frac{1}{2}(x - 4). \]
- Nous développons l'équation : \[ y - 2 = -\frac{1}{2}x + 2. \]
- Nous faisons passer le terme constant à droite : \[ y = -\frac{1}{2}x + 2 + 2 = -\frac{1}{2}x + 4. \]
Donc, l'équation de la droite cherchée est : \[ y = -\frac{1}{2}x + 4. \]
Forme implicite : Nous multiplions les deux membres par 2 :
\[ 2y = -x + 8 \quad \Rightarrow \quad x + 2y - 8 = 0. \]
Vérification : En substituant les coordonnées de \( P(4, 2) \) dans l'équation explicite :
- \[ y = -\frac{1}{2}x + 4 \quad \Rightarrow \quad 2 = -\frac{1}{2} \cdot 4 + 4 = -2 + 4 = 2. \]
Le point appartient à la droite, donc la solution est correcte.
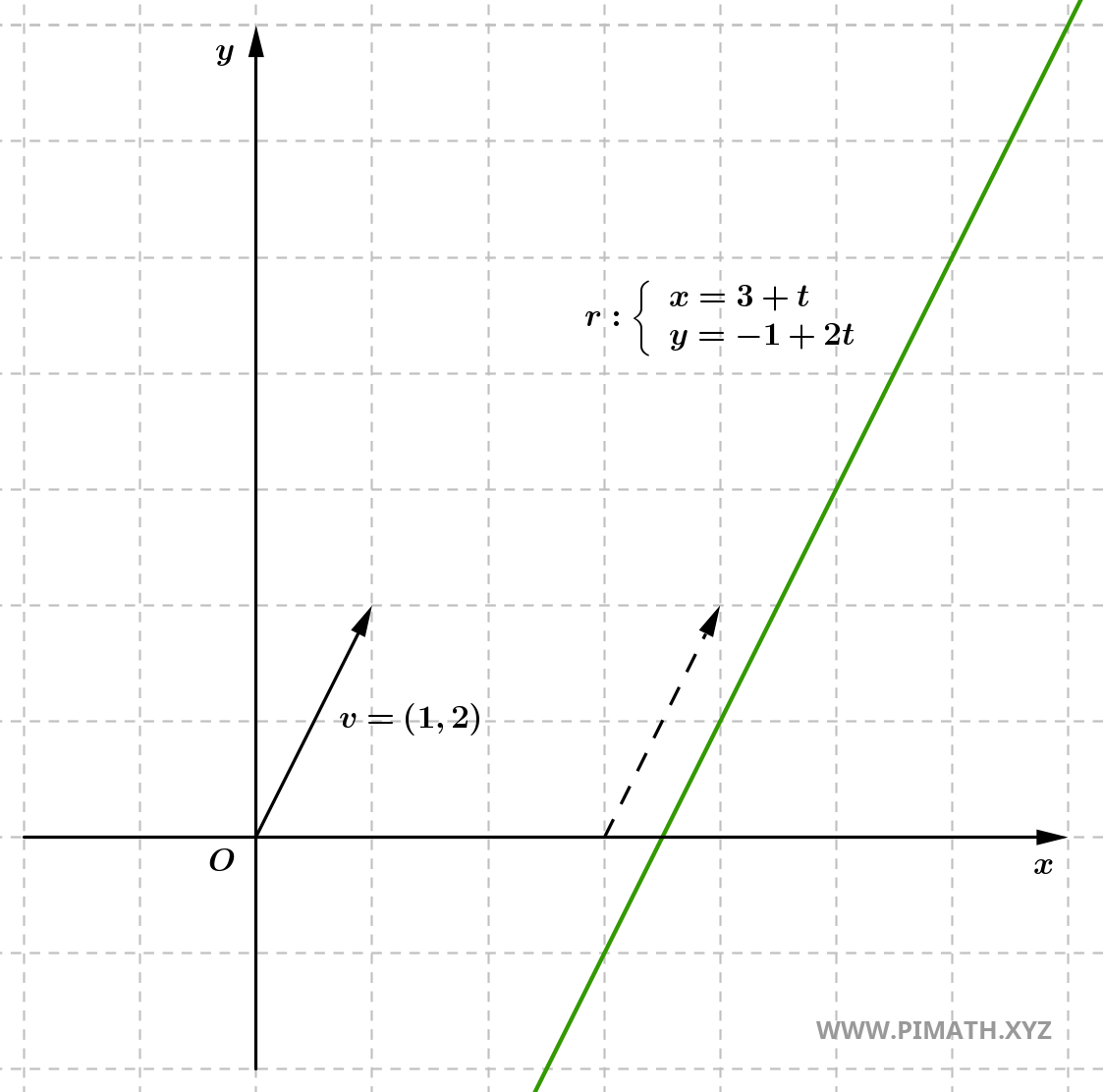
Exercice 5 : Écrire l'équation paramétrique de la droite passant par \( A(3, -1) \) et \( B(4, 1) \). Ensuite, écrire l'équation paramétrique sous forme cartésienne.
Solution. Nous calculons le vecteur directeur \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), qui représente la direction de la droite :
\[ \boldsymbol{v} = (4 - 3,\ 1 - (-1)) = (1,\ 2). \]
Les équations paramétriques de la droite sont :
\[ d: \begin{cases} x = 3 + t \\ y = -1 + 2t \end{cases} \quad \text{avec} \quad t \in \mathbb{R}. \]
Passons maintenant à la forme cartésienne. Nous tirons \( t \) de la première équation :
\[ x = 3 + t \quad \Rightarrow \quad t = x - 3. \]
En substituant dans la seconde :
\[ y = -1 + 2(x - 3) = -1 + 2x - 6 = 2x - 7. \]
Donc la forme explicite est :
\[ y = 2x - 7. \]
Enfin, en faisant passer tout au premier membre nous obtenons la forme implicite :
\[ 2x - y - 7 = 0. \]