La parabole est le lieu géométrique des points du plan pour lesquels la distance à un point fixe (foyer) est égale à la distance à une droite fixe (directrice). Elle possède un axe de symétrie qui passe par le foyer et est perpendiculaire à la directrice. C'est une courbe ouverte et symétrique par rapport à son propre axe, avec de nombreuses applications en physique et en géométrie.
Sommaire
- Équation Canonique de la Parabole
- Équation Canonique d'une Parabole à Axe Vertical ou Horizontal
- Parabole Translatée dans le Plan
- Sommet, Foyer, Directrice et Axes de Symétrie
- Équation de la Parabole Connaissant le Sommet et un Point
- Exercices Résolus sur la Parabole
Équation Canonique de la Parabole
Une parabole est le lieu géométrique des points \( P(x, y) \) du plan qui ont la même distance à un point fixe, appelé foyer, et à une droite fixe, appelée directrice.
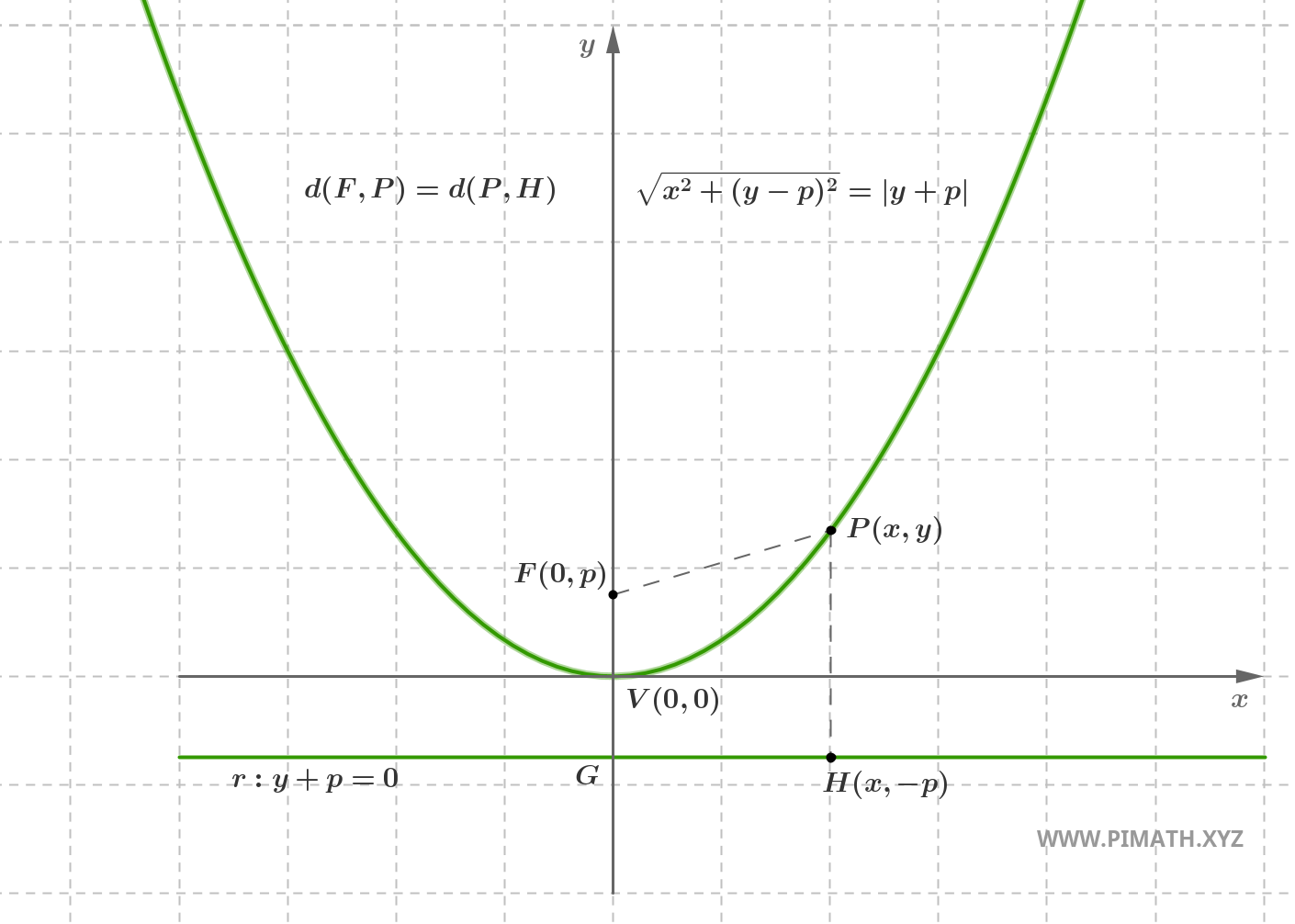
Soit \( F(0, p) \) avec \( p > 0 \) le foyer et soit \( r \) la directrice, d'équation \( y = -p \). Par définition, les points \( P(x, y) \) de la parabole satisfont :
\[ \text{d}(P, F) = \text{d}(P, r) \]
Calculons la distance entre \( P(x, y) \) et le foyer \( F(0, p) \) :
\[ \text{d}(P, F) = \sqrt{(x - 0)^2 + (y - p)^2} = \sqrt{x^2 + (y - p)^2} \]
Maintenant, calculons la distance entre \( P(x, y) \) et la droite directrice \( y = -p \) :
\[ \text{d}(P, r) = |y - (-p)| = |y + p| \]
Enfin, imposons l'égalité entre les deux distances :
\[ \sqrt{x^2 + (y - p)^2} = |y + p| \]
Observation : puisque la parabole se trouve au-dessus de la directrice (étant donné que le foyer est au-dessus de la directrice pour \( p > 0 \)), tous les points de la parabole satisfont \( y \geq -p \). Donc \( y + p \geq 0 \) et nous pouvons enlever la valeur absolue :
\[ \sqrt{x^2 + (y - p)^2} = y + p \]
Élevons au carré les deux membres :
\[ x^2 + (y - p)^2 = (y + p)^2 \]
Développons les carrés :
\[ x^2 + y^2 - 2py + p^2 = y^2 + 2py + p^2 \]
Simplifions les deux côtés :
\[ x^2 - 2py = 2py \]
Portons tout au second membre :
\[ x^2 = 4py \]
Finalement, divisons par \( 4p \) :
\[ y = \frac{1}{4p}x^2 \]
Si nous posons \( a = \displaystyle \frac{1}{4p} \), nous obtenons la forme plus compacte :
\[ y = ax^2 \]
qui est l'équation canonique de la parabole avec sommet à l'origine \( V(0, 0) \), foyer en \( F(0, p) \) et directrice \( y = -p \).
En résumé, la parabole d'équation \( y = ax^2 \) a un axe de symétrie vertical, coïncidant avec l'axe \( y \), et la concavité dirigée vers le haut si \( a > 0 \), ou vers le bas si \( a < 0 \).
Équation Canonique d'une Parabole à Axe Vertical ou Horizontal
L'équation canonique de la parabole assume des formes différentes selon l'orientation de l'axe de symétrie. Nous distinguons deux cas fondamentaux selon que l'axe soit vertical ou horizontal.
Parabole à Axe Vertical
Pour une parabole à axe de symétrie vertical, parallèle à l'axe des ordonnées, l'équation canonique est \( y = ax^2 \) ou, sous la forme équivalente, \( x^2 = 4py \). Dans cette configuration, le coefficient \( a = \displaystyle \frac{1}{4p} \) représente le coefficient directeur, tandis que \( p \) est le paramètre focal qui indique la distance du sommet au foyer.
Les éléments caractéristiques sont : le Sommet : \( V(0, 0) \), le Foyer \( F\left(0, \displaystyle \frac{1}{4a}\right) \), la Directrice : \( y = -\displaystyle\frac{1}{4a} \), l'Axe de symétrie : \( x = 0 \) (axe \( y \)) et la Concavité : vers le haut si \( a > 0 \), vers le bas si \( a < 0 \)
Exemple : Considérons la parabole \( y = 2x^2 \). Ici \( a = 2 \), donc \( p = \displaystyle \frac{1}{4a} = \displaystyle \frac{1}{8} \). Le sommet est \( V(0, 0) \), le foyer se trouve en \( F\left(0, \displaystyle \frac{1}{8}\right) \) et la directrice a pour équation \( y = -\displaystyle \frac{1}{8} \). Puisque \( a > 0 \), la parabole présente une concavité vers le haut.
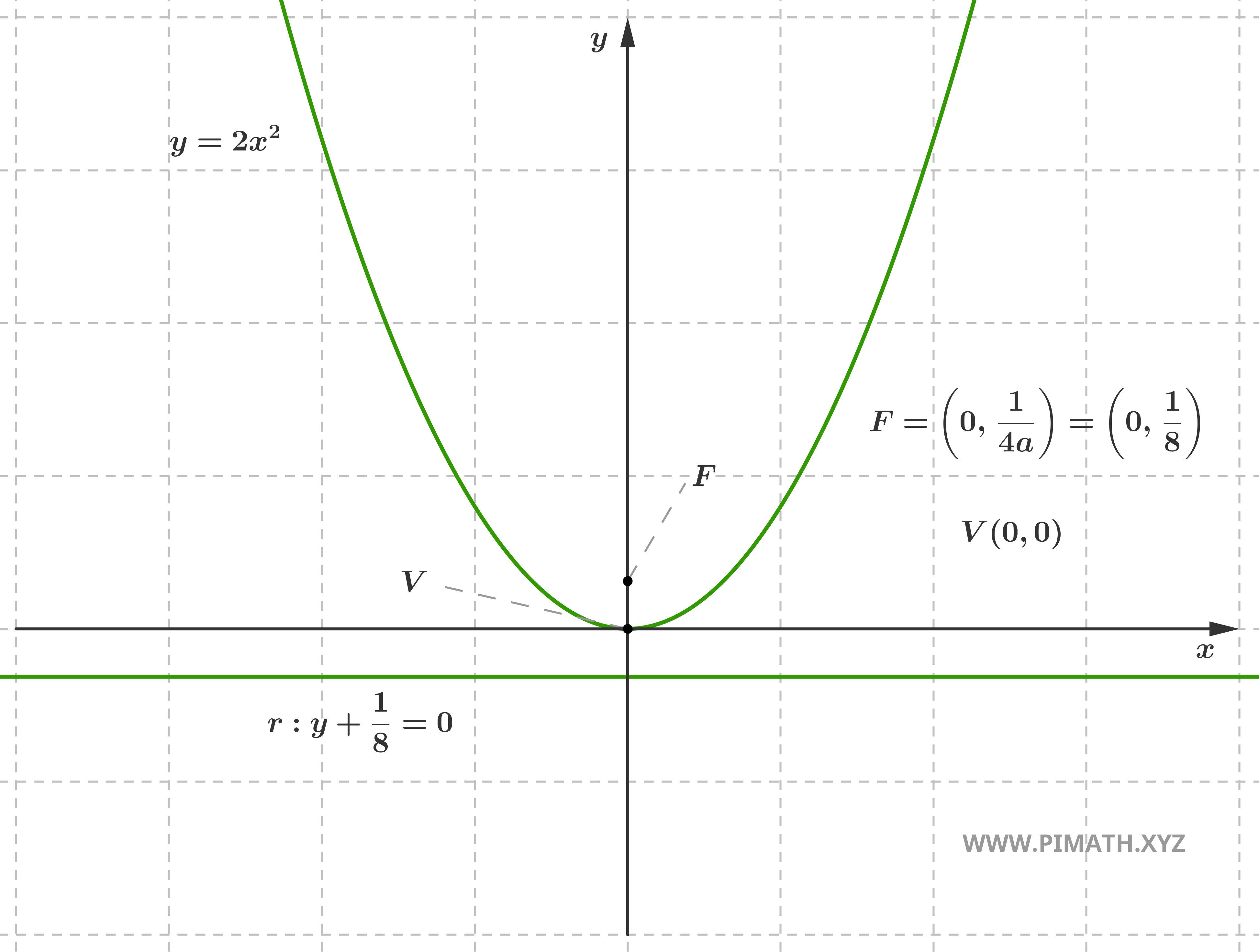
Parabole à Axe Horizontal
Pour une parabole à axe de symétrie horizontal, parallèle à l'axe des abscisses, l'équation canonique devient \( x = ay^2 \) (si nous prenons le foyer en \( (p, 0) \)), ou, de manière équivalente, \( y^2 = 4px \). Dans ce cas aussi, \( a = \displaystyle \frac{1}{4p} \) est le coefficient directeur et \( p \) représente le paramètre focal.
Éléments caractéristiques : le Sommet : \( V(0, 0) \), le Foyer : \( F\left(\displaystyle \frac{1}{4a}, 0\right) \), la Directrice : \( x = -\displaystyle \frac{1}{4a} \) l'Axe de symétrie : \( y = 0 \) (axe \( x \)), et la Concavité : vers la droite si \( a > 0 \), vers la gauche si \( a < 0 \).
Exemple : Considérons la parabole \( x = \displaystyle 2y^2 \). Ici \( a = 2 \), donc \( p = \displaystyle \frac{1}{4a} = \frac{1}{8} \). Le sommet est \( V(0, 0) \), le foyer se trouve en \( F\left(\displaystyle \frac{1}{8}, 0\right) \) et la directrice a pour équation \( x = -\displaystyle \frac{1}{8} \). Puisque \( a > 0 \), la parabole présente une concavité vers la droite.
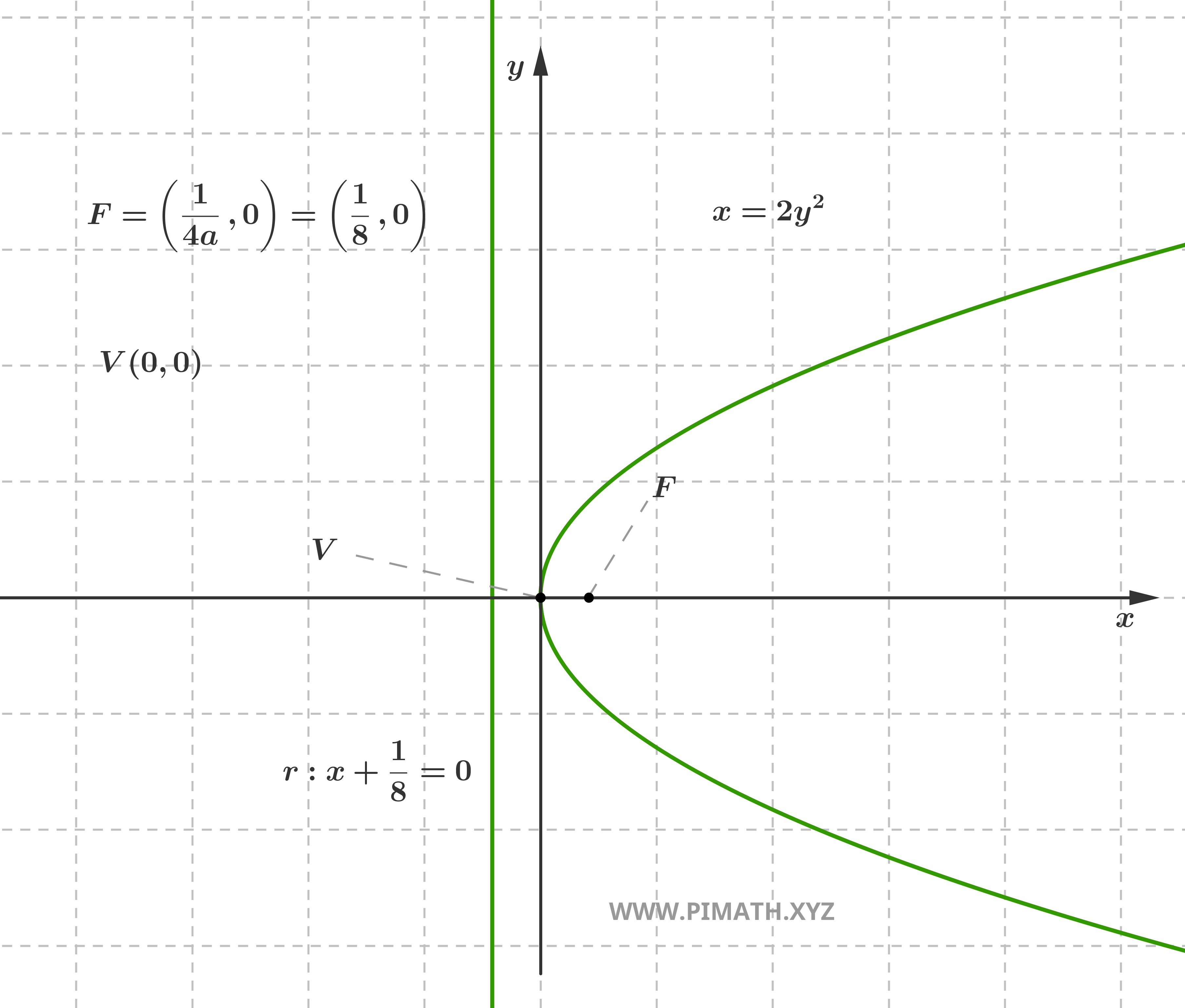
Relation entre les Paramètres
Il est fondamental de comprendre la relation qui lie le coefficient \( a \) au paramètre focal \( p \), exprimée par la formule \( a = \displaystyle \frac{1}{4p} \), qui équivaut à \( p = \displaystyle \frac{1}{4a} \). Cette relation nous permet de convertir facilement d'une forme à l'autre de l'équation canonique et de déterminer immédiatement les caractéristiques géométriques de la parabole une fois connu l'un des deux paramètres.
Indépendamment de l'orientation de l'axe de symétrie, chaque point \( P(x, y) \) appartenant à la parabole respecte toujours la propriété caractéristique qui définit géométriquement cette conique : la distance du point au foyer est toujours égale à la distance du point à la directrice.
Parabole Translatée dans le Plan
Une parabole translatée s'obtient en opérant une transformation du plan cartésien (translation). Ce type de transformation géométrique maintient inaltérée la forme de la parabole, en modifiant seulement sa position, et représente l'un des outils les plus importants pour décrire des paraboles avec sommet en des points arbitraires du plan.
Transformation de Translation
La translation est une transformation géométrique qui déplace chaque point du plan d'un vecteur constant \( \vec{v} = (h, k) \). Si nous appliquons une translation de vecteur \( (h, k) \) à la parabole canonique \( y = ax^2 \), nous obtenons une nouvelle parabole dont le sommet se déplace de l'origine au point \( V(h, k) \).
Équation de la Parabole Translatée à Axe Vertical
En partant de la parabole canonique \( y = ax^2 \) avec sommet à l'origine, une translation de vecteur \( (h, k) \) produit la parabole translatée d'équation :
\[ y = a(x - h)^2 + k \]
Ceci est la forme du sommet de l'équation parabolique. Le paramètre \( a \) maintient sa signification originaire et détermine l'ouverture et l'orientation de la parabole, tandis que \( h \) et \( k \) représentent respectivement la translation horizontale et verticale du sommet.
En développant l'expression \( (x - h)^2 = x^2 - 2hx + h^2 \), nous obtenons la forme développée :
\[ y = ax^2 - 2ahx + ah^2 + k \]
En posant \( b = -2ah \) et \( c = ah^2 + k \), nous retrouvons la forme générale \( y = ax^2 + bx + c \). De cette relation nous pouvons déduire que \( h = -\displaystyle \frac{b}{2a} \) et \( k = c - ah^2 = c - \displaystyle \frac{b^2}{4a} \).
Éléments Géométriques de la Parabole Translatée
Pour une parabole translatée \( y = a(x - h)^2 + k \), tous les éléments géométriques caractéristiques subissent la même translation appliquée à la parabole canonique : le Sommet : \( V(h, k) \), l'Axe de symétrie : \( x = h \), le Foyer : \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \) et la Directrice : \( y = k - \displaystyle \frac{1}{4a} \).
La distance entre foyer et directrice reste invariée et égale à \( 2p = \displaystyle \frac{1}{2|a|} \), ainsi que toutes les propriétés métriques de la parabole.
Exemple de Parabole Translatée
Considérons la parabole \( y = 2(x - 3)^2 - 5 \). Ceci est une parabole obtenue en translatant la parabole canonique \( y = 2x^2 \) de \( 3 \) unités vers la droite et \( 5 \) unités vers le bas.
Le sommet se trouve au point \( V(3, -5) \), l'axe de symétrie a pour équation \( x = 3 \). Le paramètre focal est \( p = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \).
Sommet, Foyer, Directrice et Axes de Symétrie
Les éléments géométriques caractéristiques d'une parabole sont le sommet, le foyer et la directrice. Ces trois éléments sont reliés entre eux et déterminent complètement la forme et la position de la parabole dans le plan cartésien.
Le Sommet de la Parabole
Définition. Le sommet est le point de la parabole qui réalise l'extremum absolu (maximum ou minimum, selon le signe de \( a \)) de la fonction quadratique \( f(x) = ax^2 + bx + c \).
Les coordonnées du sommet sont :
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
où \( \Delta = b^2 - 4ac \) est le discriminant.
Démonstration. Transformons l'équation \( y = ax^2 + bx + c \) en forme canonique par complétion du carré :
\[ y = a\left(x^2 + \frac{b}{a}x\right) + c \]
\[ y = a\left(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2\right) + c \]
\[ y = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a} \]
De la forme canonique \( y = a(x - h)^2 + k \) on lit le sommet \( V(h, k) \), donc
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
Propriétés du sommet :
- Il se trouve sur l'axe de symétrie \( x = -\displaystyle \frac{b}{2a} \)
- C'est un point de minimum si \( a > 0 \), de maximum si \( a < 0 \)
- C'est le point de la parabole le plus proche de la directrice
Le Foyer de la Parabole
Définition. Le foyer est le point fixe tel que chaque point de la parabole est équidistant du foyer et de la directrice.
Coordonnées du foyer :
\[ F\left(-\frac{b}{2a}, -\frac{\Delta}{4a} + \frac{1}{4a}\right) \]
Démonstration. Dans la forme canonique translatée \( Y = aX^2 \) (avec \( X = x + \displaystyle \frac{b}{2a} \), \( Y = y + \displaystyle \frac{\Delta}{4a} \)), le foyer se trouve en \( \left(0, \displaystyle \frac{1}{4a}\right) \).
Pour le vérifier, considérons un point \( P(X_0, aX_0^2) \) sur la parabole. La distance du foyer candidat \( F\left(0, \displaystyle \frac{1}{4a}\right) \) est :
\[ d(P,F) = \sqrt{X_0^2 + \left(aX_0^2 - \frac{1}{4a}\right)^2} \]
La distance de la directrice candidate \( Y = -\displaystyle \frac{1}{4a} \) est :
\[ d(P,d) = \left|aX_0^2 + \frac{1}{4a}\right| \]
Pour \( a > 0 \), en élevant au carré et en simplifiant, on vérifie que \( d(P,F) = d(P,d) \) pour chaque point \( P \) de la parabole.
En revenant au système original, on obtient les coordonnées indiquées.
Paramètre focal : La distance du sommet au foyer est \( p = \displaystyle \frac{1}{4|a|} \).
La Directrice de la Parabole
Définition. La directrice est la droite fixe telle que chaque point de la parabole est équidistant de la directrice et du foyer.
Équation de la directrice :
\[ y = -\frac{\Delta}{4a} - \frac{1}{4a} \]
Démonstration. De la vérification de l'équidistance pour la forme canonique, la directrice a pour équation \( Y = -\displaystyle \frac{1}{4a} \) dans le système translaté. En revenant au système original : \( y = Y - \displaystyle \frac{\Delta}{4a} = -\displaystyle \frac{1}{4a} - \displaystyle \frac{\Delta}{4a} \).
Propriétés de la directrice :
- Elle est perpendiculaire à l'axe de symétrie
- Elle se trouve à distance \( p = \displaystyle \frac{1}{4|a|} \) du sommet, opposée au foyer
- La distance foyer-directrice est \( 2p = \displaystyle \frac{1}{2|a|} \)
L'Axe de Symétrie
L'axe de symétrie est la droite qui passe par le sommet et le foyer, par rapport à laquelle la parabole est parfaitement symétrique. Pour une parabole à axe vertical d'équation \( y = ax^2 + bx + c \), l'axe de symétrie a pour équation \( x = -\displaystyle \frac{b}{2a} \).
Chaque point de la parabole a un point symétrique par rapport à l'axe de symétrie. Si \( P(x_0, y_0) \) appartient à la parabole, alors le point \( P'(2x_V - x_0, y_0) \) appartient aussi à la parabole, où \( x_V \) est l'abscisse du sommet.
Relations entre les Éléments
Système coordonné : Les trois éléments forment un système avec des relations précises :
- Sommet et foyer se trouvent sur l'axe de symétrie \( x = -\displaystyle \frac{b}{2a} \)
- La directrice est perpendiculaire à l'axe de symétrie
- Le sommet est équidistant du foyer et de la directrice (distance = paramètre focal \( p \))
- Si \( a > 0 \) : foyer au-dessus du sommet, directrice en dessous
- Si \( a < 0 \) : foyer en dessous du sommet, directrice au-dessus
Exemple Complet
Considérons la parabole d'équation \( y = 2x^2 - 8x + 3 \). Déterminons tous les éléments caractéristiques.
Tout d'abord, identifions les coefficients : \( a = 2 \), \( b = -8 \), \( c = 3 \). Le discriminant est \( \Delta = b^2 - 4ac = 64 - 24 = 40 \).
Le sommet a pour coordonnées \( V\left(-\displaystyle \frac{(-8)}{2 \cdot 2}, -\displaystyle \frac{40}{4 \cdot 2}\right) = V(2, -5) \).
L'axe de symétrie a pour équation \( x = 2 \).
Puisque \( a = 2 \), le paramètre focal est \( p = \displaystyle \frac{1}{4|a|} = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \). Puisque \( a > 0 \), la parabole a une concavité vers le haut, donc le foyer se trouve au-dessus du sommet : \( F\left(2, -5 + \displaystyle \frac{1}{8}\right) = F\left(2, -\displaystyle \frac{39}{8}\right) \).
La directrice se trouve en dessous du sommet à distance \( p \) : \( y = -5 - \displaystyle \frac{1}{8} = -\displaystyle \frac{41}{8} \).
Formes Particulières
Forme canonique \( y = ax^2 \) :
- Sommet : \( V(0, 0) \)
- Foyer : \( F\left(0, \displaystyle \frac{1}{4a}\right) \)
- Directrice : \( y = -\displaystyle \frac{1}{4a} \)
Forme translatée \( y = a(x - h)^2 + k \) :
- Sommet : \( V(h, k) \)
- Foyer : \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \)
- Directrice : \( y = k - \displaystyle \frac{1}{4a} \)
Équation de la Parabole Connaissant le Sommet et un Point
Lorsque le sommet de la parabole et un autre point appartenant à la courbe sont connus, il est possible de déterminer de manière univoque l'équation de la parabole. Cette méthode est particulièrement utile dans les applications pratiques où l'on connaît le point de minimum ou maximum d'une fonction quadratique et une valeur spécifique prise par la fonction.
Forme Générale avec Sommet Assigné
Étant donnée une parabole avec sommet \( V(h, k) \), l'équation la plus commode à utiliser est la forme du sommet, qui pour une parabole à axe vertical s'écrit comme \( y = a(x - h)^2 + k \), où \( a \) est le paramètre à déterminer qui contrôle l'ouverture et l'orientation de la parabole.
Procédure pour Paraboles à Axe Vertical
Soit \( V(h, k) \) le sommet de la parabole et soit \( P(x_0, y_0) \) un point appartenant à la parabole avec \( x_0 \neq h \). En substituant les coordonnées du point \( P \) dans l'équation \( y = a(x - h)^2 + k \), nous obtenons :
\[ y_0 = a(x_0 - h)^2 + k \]
De cette équation nous pouvons tirer directement la valeur du paramètre \( a \) :
\[ a = \frac{y_0 - k}{(x_0 - h)^2} \]
Une fois déterminé \( a \), l'équation complète de la parabole devient \( y = \displaystyle \frac{y_0 - k}{(x_0 - h)^2}(x - h)^2 + k \).
Exemple Numérique - Axe Vertical
Déterminons l'équation de la parabole avec sommet \( V(3, -2) \) et passant par le point \( P(5, 6) \).
Utilisons la forme du sommet \( y = a(x - 3)^2 - 2 \) et substituons les coordonnées du point \( P(5, 6) \) :
\[ 6 = a(5 - 3)^2 - 2 \]
\[ 6 = a \cdot 4 - 2 \]
\[ 8 = 4a \]
\[ a = 2 \]
L'équation de la parabole est donc \( y = 2(x - 3)^2 - 2 \). En développant cette expression nous obtenons \( y = 2(x^2 - 6x + 9) - 2 = 2x^2 - 12x + 18 - 2 = 2x^2 - 12x + 16 \).
Pour vérifier la justesse, contrôlons que le sommet soit effectivement \( V(3, -2) \). L'abscisse du sommet est \( x_V = -\displaystyle \frac{b}{2a} = -\displaystyle \frac{-12}{2 \cdot 2} = 3 \) et l'ordonnée est \( y_V = 2 \cdot 3^2 - 12 \cdot 3 + 16 = 18 - 36 + 16 = -2 \).
Procédure pour Paraboles à Axe Horizontal
Pour des paraboles à axe horizontal, l'équation sous forme du sommet devient \( x = a(y - k)^2 + h \), où \( V(h, k) \) est le sommet. Étant donné un point \( P(x_0, y_0) \) appartenant à la parabole avec \( y_0 \neq k \), le paramètre \( a \) se détermine avec :
\[ a = \frac{x_0 - h}{(y_0 - k)^2} \]
Relation avec le Paramètre Focal
Une fois déterminé le coefficient \( a \), il est possible de calculer tous les autres éléments caractéristiques de la parabole. Le paramètre focal est \( p = \displaystyle \frac{1}{4|a|} \), la distance du sommet au foyer. Le foyer se trouve au point \( F(h, k + p) \) pour des paraboles à axe vertical et \( a > 0 \), tandis qu'il se trouve en \( F(h, k - p) \) si \( a < 0 \).
Exercices Résolus sur la Parabole
Exercice 1. Étant donnée la parabole d'équation \( y = 3x^2 - 12x + 7 \), déterminer sommet, foyer, directrice et paramètre focal.
Solution. De la forme générale \( y = ax^2 + bx + c \) nous identifions les coefficients \( a = 3 \), \( b = -12 \), \( c = 7 \).
Le sommet est donné par la formule \[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \] où \( \Delta = b^2 - 4ac = (-12)^2 - 4(3)(7) = 144 - 84 = 60 \). En substituant :
\[ V\left(-\frac{-12}{2 \cdot 3}, -\frac{60}{4 \cdot 3}\right) = V\left(2, -5\right) \]
Le paramètre focal est \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 3} = \frac{1}{12} \]
Puisque \( a = 3 > 0 \), la parabole a une concavité vers le haut et le foyer se trouve au-dessus du sommet :
\[ F\left(2, -5 + \frac{1}{12}\right) = F\left(2, -\frac{59}{12}\right) \]
La directrice est positionnée en dessous du sommet à la même distance que le foyer :
\[ y = -5 - \frac{1}{12} = -\frac{61}{12} \]
Exercice 2. Déterminer l'équation de la parabole à axe vertical qui a pour sommet \( V(-1, 4) \) et passe par le point \( P(2, -5) \).
Solution. Utilisons la forme du sommet \( y = a(x - h)^2 + k \) où \( V(h, k) = (-1, 4) \) :
\[ y = a(x - (-1))^2 + 4 = a(x + 1)^2 + 4 \]
Pour déterminer le paramètre \( a \), substituons les coordonnées du point \( P(2, -5) \) :
\[ -5 = a(2 + 1)^2 + 4 \]
\[ -5 = 9a + 4 \]
\[ a = \frac{-9}{9} = -1 \]
L'équation de la parabole est donc \( y = -(x + 1)^2 + 4 \).
En développant l'expression nous obtenons la forme standard :
\[ y = -(x^2 + 2x + 1) + 4 = -x^2 - 2x + 3 \]
Exercice 3. Étant donnée la parabole à axe horizontal \( x = 2y^2 - 8y + 6 \), déterminer sommet, foyer et directrice.
Solution. Pour identifier le sommet, complétons le carré par rapport à la variable \( y \) :
\begin{align} x &= 2(y^2 - 4y) + 6 \\ &= 2(y^2 - 4y + 4 - 4) + 6 \\ &= 2(y - 2)^2 - 8 + 6 \\ &= 2(y - 2)^2 - 2 \end{align}
De la forme \( x = a(y - k)^2 + h \) nous lisons directement le sommet \( V(h, k) = V(-2, 2) \).
Le paramètre focal est \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 2} = \frac{1}{8} \]
Puisque \( a = 2 > 0 \), la parabole s'ouvre vers la droite et le foyer se trouve à droite du sommet :
\[ F\left(-2 + \frac{1}{8}, 2\right) = F\left(-\frac{15}{8}, 2\right) \]
La directrice est la droite verticale positionnée à gauche du sommet :
\[ x = -2 - \frac{1}{8} = -\frac{17}{8} \]
Exercice 4. Étant donnée la parabole \( y = -2x^2 + 8x - 5 \), déterminer l'équation de la parabole symétrique par rapport à l'axe des abscisses. Calculer également les points d'intersection entre les deux paraboles.
Solution. La parabole symétrique par rapport à l'axe des abscisses s'obtient en changeant le signe de la variable \( y \). De l'équation originale \( y = -2x^2 + 8x - 5 \), la parabole symétrique a pour équation :
\[ y = 2x^2 - 8x + 5 \]
Pour trouver les points d'intersection, résolvons le système formé par les deux paraboles :
\[ \begin{cases} y = -2x^2 + 8x - 5 \\ y = 2x^2 - 8x + 5 \end{cases} \]
En égalisant les deux expressions :
\[ -2x^2 + 8x - 5 = 2x^2 - 8x + 5 \]
\[ -4x^2 + 16x - 10 = 0 \]
\[ -2(2x^2 - 8x + 5) = 0 \]
\[ 2x^2 - 8x + 5 = 0 \]
En appliquant la formule quadratique :
\[ x = \frac{8 \pm \sqrt{64 - 40}}{4} = \frac{8 \pm \sqrt{24}}{4} = \frac{8 \pm 2\sqrt{6}}{4} = \frac{4 \pm \sqrt{6}}{2} \]
Les ordonnées correspondantes se calculent en substituant dans l'une des deux équations :
Pour \( x_1 = \displaystyle \frac{4 + \sqrt{6}}{2} \) : \( y_1 = 2\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Pour \( x_2 = \displaystyle \frac{4 - \sqrt{6}}{2} \) : \( y_2 = 2\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Les points d'intersection sont :
\[ A\left(\frac{4 + \sqrt{6}}{2}, -\frac{1}{2}\right) \quad \text{et} \quad B\left(\frac{4 - \sqrt{6}}{2}, -\frac{1}{2}\right) \]
Étant tous deux à la même ordonnée, la distance entre eux est simplement :
\[ d(A,B) = \left|\frac{4 + \sqrt{6}}{2} - \frac{4 - \sqrt{6}}{2}\right| = \left|\frac{2\sqrt{6}}{2}\right| = \sqrt{6} \]
Exercice 5. Déterminer l'équation de la parabole à axe vertical qui a pour foyer \( F(1, 5) \) et directrice \( y = 3 \). Vérifier si le point \( P(3, 6) \) appartient à la parabole.
Solution. Le sommet de la parabole est le point équidistant du foyer et de la directrice, situé sur la droite perpendiculaire à la directrice et passant par le foyer. Puisque la directrice est horizontale, le sommet a la même abscisse que le foyer et une ordonnée égale à la moyenne arithmétique :
\[ V\left(1, \frac{5 + 3}{2}\right) = V(1, 4) \]
Le paramètre focal est la distance du sommet au foyer :
\[ p = |5 - 4| = 1 \]
Le coefficient de la parabole est donc :
\[ a = \frac{1}{4p} = \frac{1}{4 \cdot 1} = \frac{1}{4} \]
L'équation de la parabole sous la forme du sommet est :
\[ y = \frac{1}{4}(x - 1)^2 + 4 \]
Pour vérifier si \( P(3, 6) \) appartient à la parabole, substituons ses coordonnées :
\[ y = \frac{1}{4}(3 - 1)^2 + 4 = \frac{1}{4} \cdot 4 + 4 = 1 + 4 = 5 \neq 6 \]
Confirmons le résultat en utilisant la définition géométrique de la parabole. La distance de P au foyer est :
\[ d(P,F) = \sqrt{(3-1)^2 + (6-5)^2} = \sqrt{4 + 1} = \sqrt{5} \]
La distance de P à la directrice est :
\[ d(P, \text{directrice}) = |6 - 3| = 3 \]
Puisque \( \sqrt{5} \neq 3 \), le point \( P(3, 6) \) n'appartient pas à la parabole.

