L'étude des positions relatives de deux droites est l'un des sujets fondamentaux de la géométrie analytique plane. Comprendre comment deux droites peuvent se positionner dans le plan cartésien permet de classifier avec précision toutes les situations géométriques possibles : de l'intersection en un point unique jusqu'à la superposition complète.
Sommaire
- Représentation des droites dans le plan
- Classification des positions relatives
- Droites perpendiculaires
- Exercices résolus
Représentation des droites dans le plan
Étant données deux droites dans le plan, trois configurations principales peuvent se présenter :
- Droites confondues : il s'agit de deux équations qui décrivent en réalité la même droite. Dans ce cas, les droites ont tous les points en commun et sont indiscernables du point de vue géométrique.
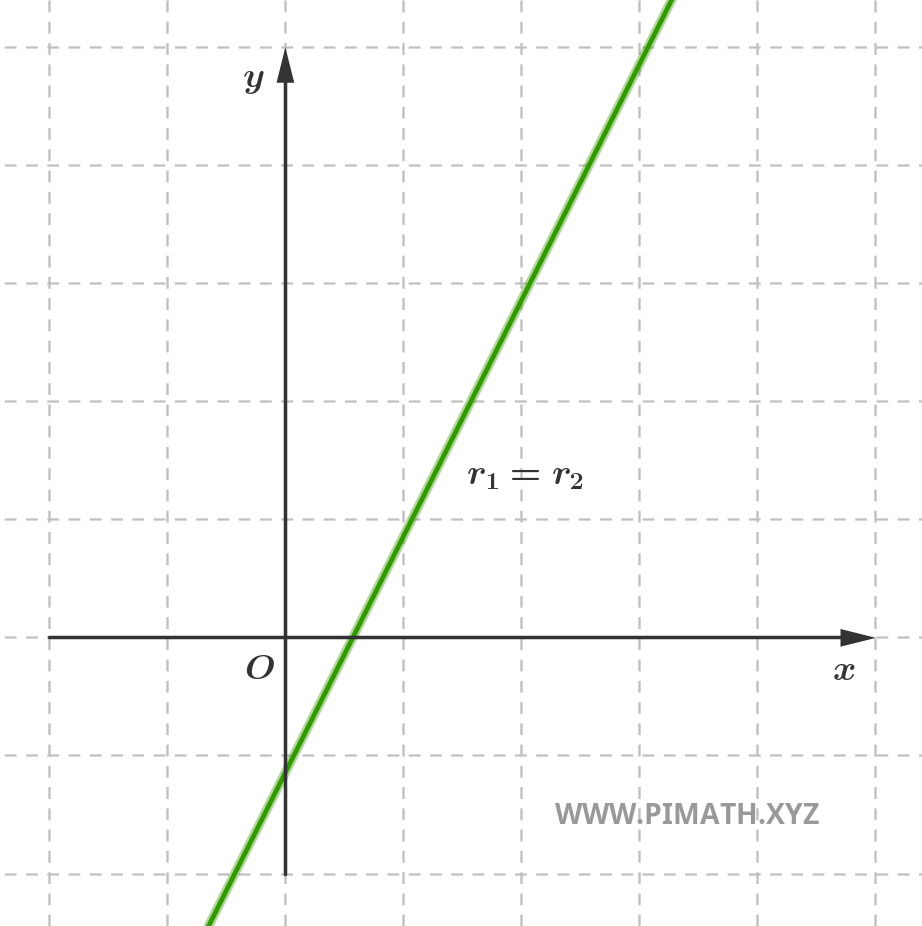
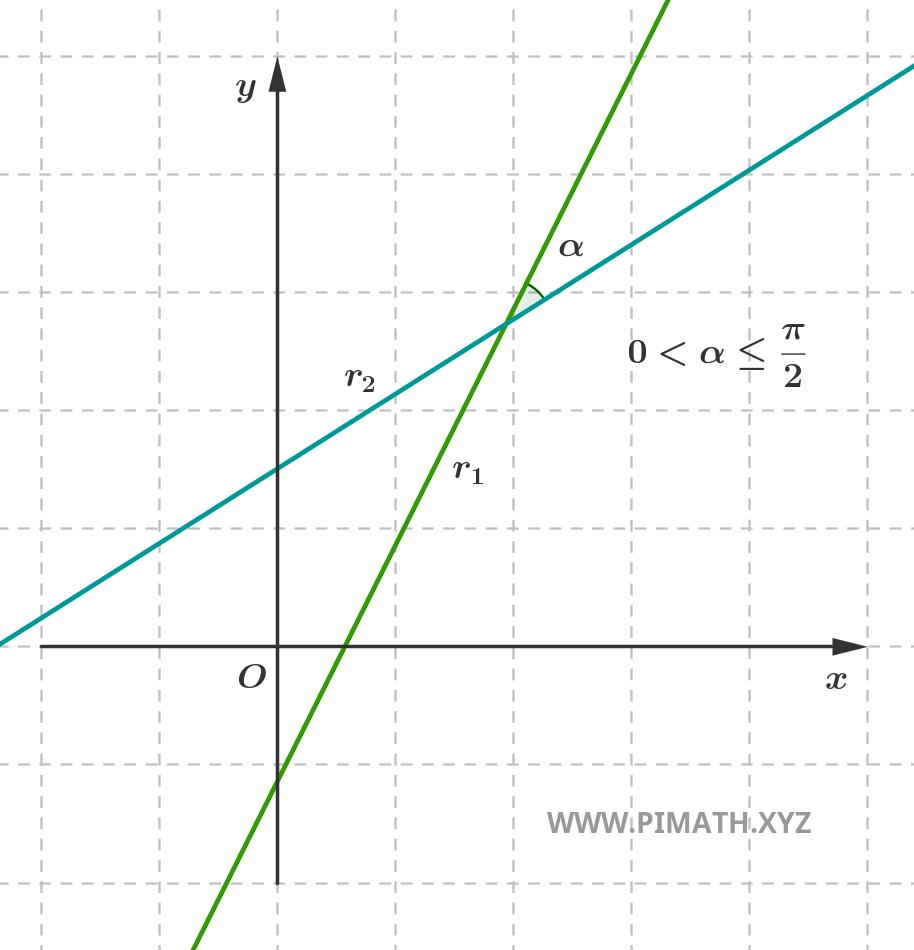
- Droites sécantes : elles s'intersectent en un seul point du plan, formant un angle qui peut prendre n'importe quelle amplitude comprise entre 0° et 180°, à l'exclusion des cas de parallélisme.
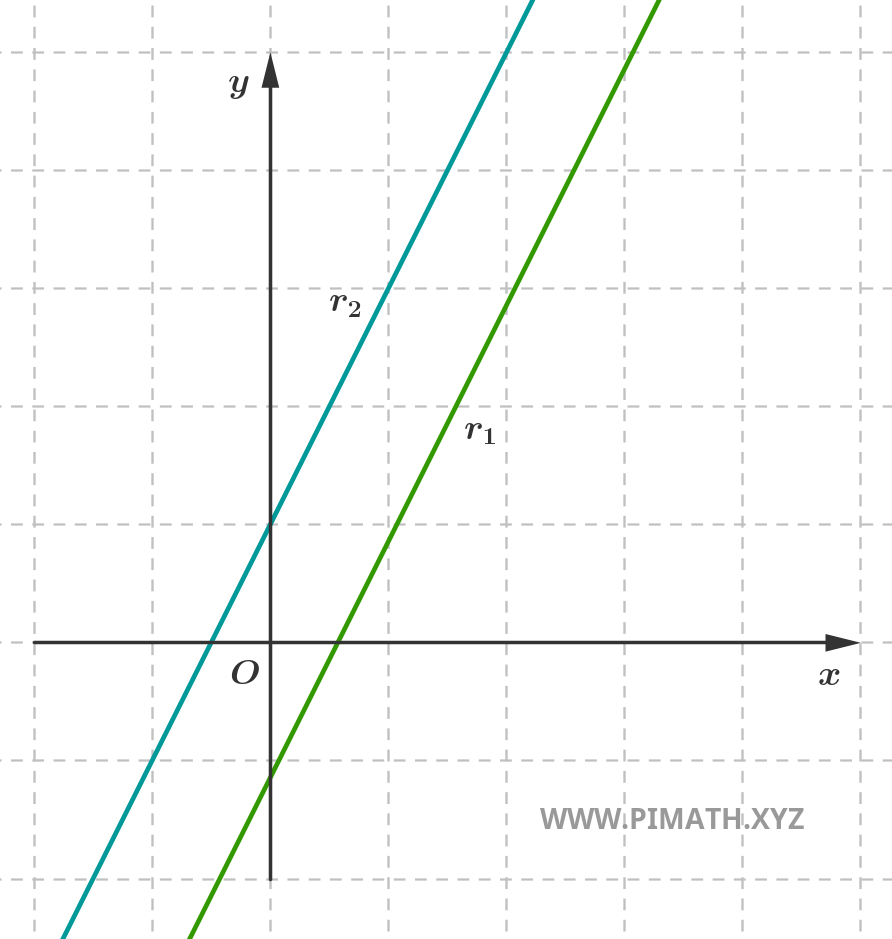
- Droites parallèles distinctes : bien qu'ayant la même inclinaison (c'est-à-dire le même coefficient directeur), ces droites ne se rencontrent jamais. Elles ne partagent aucun point.
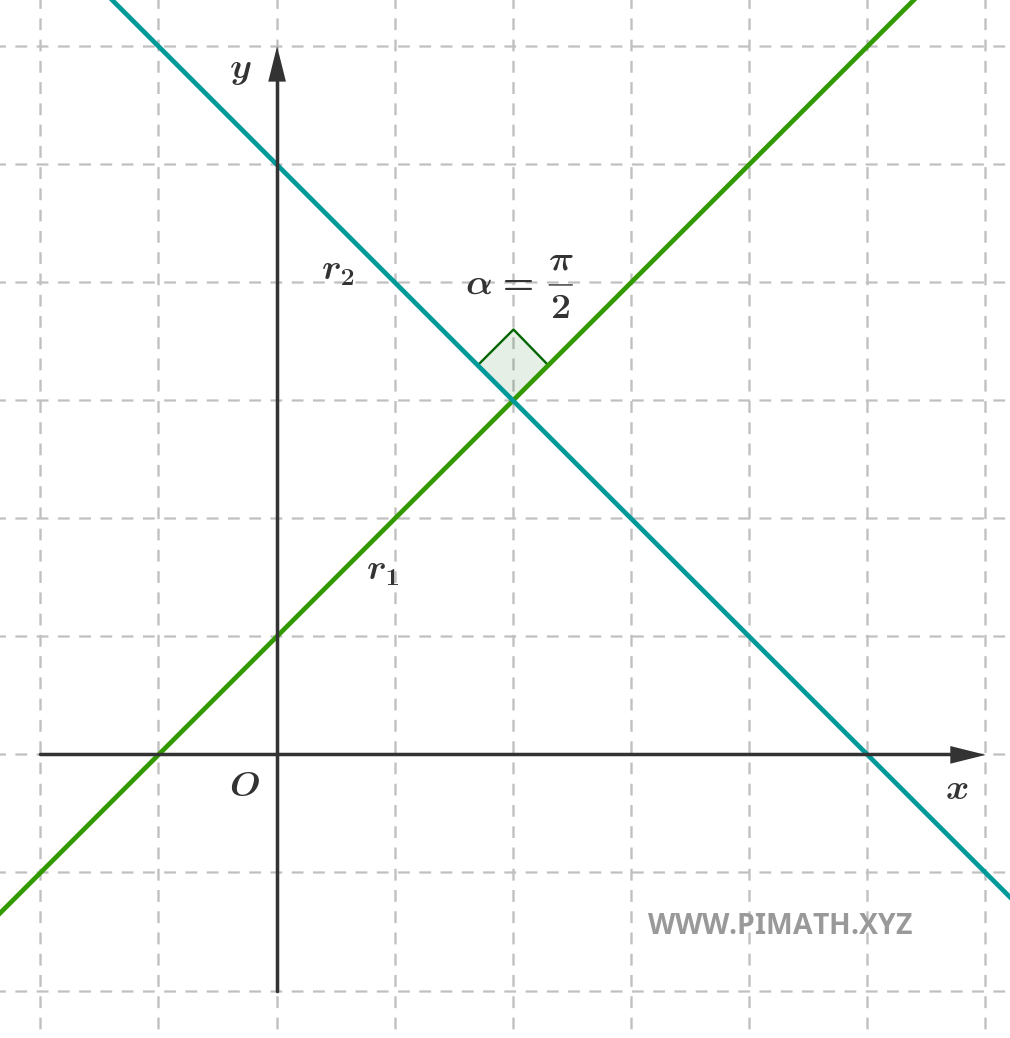
Au sein des droites sécantes se trouve un cas particulier très important : celui des droites perpendiculaires. Deux droites sont perpendiculaires si elles s'intersectent en formant un angle droit \( \displaystyle \frac{\pi}{2} \) (soit 90°).
Formes de l'équation d'une droite
Une droite dans le plan cartésien peut être représentée de plusieurs manières, équivalentes entre elles mais utiles dans des contextes différents.
La forme explicite, également appelée forme réduite, est peut-être la plus intuitive :
\[ y = mx + b \]
Dans cette équation :
Le paramètre \( m \in \mathbb{R} \) est appelé coefficient directeur ou pente et représente l'inclinaison de la droite. Par convention, si la droite est verticale, on dit que le coefficient directeur est infini ou n'est pas défini.
Le terme \( b \in \mathbb{R} \) est l'ordonnée à l'origine, c'est-à-dire le point où la droite coupe l'axe \( y \).
Une autre façon d'écrire est la forme implicite, également appelée forme générale :
\[ ax + by + c = 0 \]
Dans ce cas, \( a, b, c \in \mathbb{R} \), et on doit avoir \( a^2 + b^2 \neq 0 \) pour qu'il s'agisse effectivement de l'équation d'une droite.
Relation entre les formes
Lorsque le coefficient \( b \) est différent de zéro, il est possible d'obtenir la forme explicite à partir de la forme implicite. En effet, en résolvant par rapport à \( y \), on obtient :
\[ ax + by + c = 0 \quad \Leftrightarrow \quad y = -\frac{a}{b}x - \frac{c}{b} \]
De cette façon, le coefficient directeur est \( m = -\displaystyle \frac{a}{b} \) et l'ordonnée à l'origine est \( b = -\displaystyle \frac{c}{b} \).
Si au contraire \( b = 0 \) et \( a \neq 0 \), l'équation se réduit à la forme \( x = -\displaystyle \frac{c}{a} \), qui représente une droite verticale. Dans ce cas, le coefficient directeur n'est pas défini.
Classification des positions relatives
Droites confondues
Deux droites sont confondues lorsqu'elles coïncident point par point : chaque point de l'une appartient aussi à l'autre. En substance, il s'agit de la même droite exprimée avec deux équations proportionnelles.
Si elles sont exprimées en forme explicite, on a :
\[ r: y = mx + b \quad \text{et} \quad s: y = mx + b \]
En forme implicite, deux droites \( r: a_1x + b_1y + c_1 = 0 \) et \( s: a_2x + b_2y + c_2 = 0 \) sont confondues si et seulement s'il existe une constante \( k \neq 0 \) telle que :
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} = k \]
De manière équivalente, cela signifie que \( (a_2, b_2, c_2) = k(a_1, b_1, c_1) \) pour un certain \( k \neq 0 \).
Exemple : les droites \( 2x + 3y - 6 = 0 \) et \( 4x + 6y - 12 = 0 \) sont confondues, car les coefficients de l'une sont le double de ceux de l'autre :
\[ \frac{2}{4} = \frac{3}{6} = \frac{-6}{-12} = \frac{1}{2} \]
Droites parallèles
Deux droites sont parallèles si elles ont la même direction. Dans le cas où elles ne coïncident pas, on dit qu'elles sont parallèles distinctes et n'ont aucun point en commun.
En forme explicite, la condition de parallélisme est :
\[ m_1 = m_2 \]
Si de plus \( b_1 \neq b_2 \), alors les droites sont parallèles distinctes.
En forme implicite, deux droites \( r: a_1x + b_1y + c_1 = 0 \) et \( s: a_2x + b_2y + c_2 = 0 \) sont parallèles si et seulement si :
\[ a_1b_2 - a_2b_1 = 0 \]
Cela équivaut à dire que \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \) (lorsque \( a_2, b_2 \neq 0 \)).
Pour avoir un parallélisme distinct, on doit en outre vérifier que :
\[ \frac{c_1}{c_2} \neq \frac{a_1}{a_2} \quad \text{(c'est-à-dire} \quad \frac{c_1}{c_2} \neq \frac{b_1}{b_2}\text{)} \]
Exemple : les droites \( r: y = 3x + 2 \) et \( s: y = 3x - 1 \) sont parallèles distinctes car elles ont le même coefficient directeur mais une ordonnée à l'origine différente.
Droites sécantes
Deux droites sont sécantes si elles s'intersectent en un point unique. Cela se produit lorsque les droites ont des directions différentes, c'est-à-dire des coefficients directeurs distincts (dans le cas de droites non verticales).
En forme explicite, il suffit de vérifier que :
\[ m_1 \neq m_2 \]
En forme implicite, la condition est :
\[ a_1b_2 - a_2b_1 \neq 0 \]
Point d'intersection
Pour déterminer le point d'intersection entre deux droites sécantes exprimées en forme implicite, on résout le système linéaire suivant :
\[ \begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0 \end{cases} \]
En appliquant la règle de Cramer, les coordonnées du point d'intersection sont :
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]
pourvu que \( a_1b_2 - a_2b_1 \neq 0 \).
Droites perpendiculaires
Condition de perpendicularité
Deux droites sont perpendiculaires si elles s'intersectent en formant un angle droit, c'est-à-dire de 90°.
En forme explicite, si les droites ont des coefficients directeurs \( m_1 \) et \( m_2 \) finis, la condition est :
\[ m_1 \cdot m_2 = -1 \]
Cas particulier : une droite horizontale (\( m = 0 \)) est perpendiculaire à une droite verticale (coefficient directeur non défini).
En forme implicite, deux droites \( r: a_1x + b_1y + c_1 = 0 \) et \( s: a_2x + b_2y + c_2 = 0 \) sont perpendiculaires si et seulement si :
\[ a_1a_2 + b_1b_2 = 0 \]
Cette relation découle du fait que les vecteurs normaux des deux droites, \( \vec{n}_1 = (a_1, b_1) \) et \( \vec{n}_2 = (a_2, b_2) \), sont orthogonaux, c'est-à-dire que leur produit scalaire est nul.
Démonstration analytique
L'angle \( \theta \) entre deux droites de coefficients directeurs \( m_1 \) et \( m_2 \) est exprimé par la formule :
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]
où \( \theta \) représente l'angle aigu entre les deux droites.
Si \( m_1m_2 = -1 \), le dénominateur \( 1 + m_1m_2 \) s'annule et la tangente devient indéfinie, ce qui correspond à un angle de 90°.
Exercices résolus
Exercice 1. Établir si les droites \( r: y = -2x + 1 \) et \( s: y = \displaystyle \frac{1}{2}x - 3 \) sont perpendiculaires.
Déterminons les coefficients directeurs :
\[ m_1 = -2 \]
\[ m_2 = \frac{1}{2} \]
Vérifions le produit entre les deux coefficients :
\[ m_1 \cdot m_2 = (-2) \cdot \frac{1}{2} = -1 \]
Puisque le produit est égal à -1, nous pouvons conclure que les deux droites sont perpendiculaires.
Exercice 2. Calculer l'angle aigu entre les droites \( r: y = 2x \) et \( s: y = -x \).
Les coefficients directeurs sont :
\[ m_1 = 2 \]
\[ m_2 = -1 \]
Utilisons la formule pour le calcul de l'angle aigu \( \theta \) entre deux droites :
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right| = \left| \frac{-1 - 2}{1 + 2 \cdot (-1)} \right| = \left| \frac{-3}{1 - 2} \right| = \left| \frac{-3}{-1} \right| = 3 \]
Donc :
\[ \theta = \arctan(3) \approx 71{,}57^\circ \]
Exercice 3. Trouver l'équation de la droite perpendiculaire à \( r: y = -\displaystyle \frac{3}{2}x + 4 \) et passant par le point \( P(2, 1) \).
Le coefficient directeur de la droite donnée est \( m = -\displaystyle \frac{3}{2} \).
Le coefficient directeur de la droite perpendiculaire sera l'opposé de l'inverse :
\[ m' = -\frac{1}{m} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3} \]
Utilisons la formule du faisceau propre de droites passant par \( P(2, 1) \) :
\[ y - y_0 = m'(x - x_0) \quad \text{avec } (x_0, y_0) = (2, 1) \] \[ y - 1 = \frac{2}{3}(x - 2) \] \[ y = \frac{2}{3}x - \frac{4}{3} + 1 = \frac{2}{3}x - \frac{1}{3} \]
L'équation cherchée est :
\[ y = \frac{2}{3}x - \frac{1}{3} \]
Exercice 4. Déterminer la valeur de \( k \) pour que les droites \( r: 2x + 3y - 1 = 0 \) et \( s: kx + 6y + 2 = 0 \) soient parallèles.
Deux droites en forme implicite sont parallèles si \( a_1b_2 - a_2b_1 = 0 \).
Identifions les coefficients :
- Droite \( r \) : \( a_1 = 2, b_1 = 3, c_1 = -1 \)
- Droite \( s \) : \( a_2 = k, b_2 = 6, c_2 = 2 \)
Appliquons la condition :
\[ a_1b_2 - a_2b_1 = 2 \cdot 6 - k \cdot 3 = 12 - 3k = 0 \] \[ 3k = 12 \quad \Rightarrow \quad k = 4 \]
Vérifions que pour \( k = 4 \) les droites sont effectivement parallèles distinctes :
\[ \frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \]
\[ \frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2} \]
\[ \frac{c_1}{c_2} = \frac{-1}{2} = -\frac{1}{2} \]
Puisque \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \neq \displaystyle \frac{c_1}{c_2} \), les droites sont parallèles distinctes pour \( k = 4 \).
Exercice 5. Déterminer le point d'intersection entre les droites :
\( r: x + 2y - 3 = 0 \)
\( s: 2x - y + 1 = 0 \)
Résolvons le système :
\[ \begin{cases} x + 2y = 3 \\ 2x - y = -1 \end{cases} \]
Utilisons la méthode d'élimination. Multiplions la deuxième équation par 2 :
\[ \begin{cases} x + 2y = 3 \\ 4x - 2y = -2 \end{cases} \]
Additionnons les deux équations :
\[ x + 4x + 2y - 2y = 3 + (-2) \] \[ 5x = 1 \quad \Rightarrow \quad x = \frac{1}{5} \]
Substituons dans la première équation :
\[ \frac{1}{5} + 2y = 3 \quad \Rightarrow \quad 2y = 3 - \frac{1}{5} = \frac{15 - 1}{5} = \frac{14}{5} \] \[ y = \frac{7}{5} \]
Le point d'intersection est :
\[ \left( \frac{1}{5}, \frac{7}{5} \right) \]
Vérification : en substituant dans les deux équations originales on obtient l'identité \( 0 = 0 \), confirmant la justesse du résultat.

