Les fonctions paires et fonctions impaires se distinguent par leurs symétries : les fonctions paires sont symétriques par rapport à l'axe des ordonnées, tandis que les fonctions impaires le sont par rapport à l'origine. Nous approfondirons également le comportement de la somme de fonctions : la somme de deux fonctions paires est encore une fonction paire, de même que la somme de deux fonctions impaires est encore impaire. Enfin, nous verrons comment décomposer une fonction en sa partie paire et sa partie impaire.
- Fonctions Paires
- Somme de deux fonctions paires
- Fonctions Impaires
- Somme de deux fonctions impaires
- Fonctions ni paires ni impaires
- Intégration sur des intervalles symétriques
- Décomposition d'une fonction en partie paire et partie impaire
- Démonstration de l'unicité de la décomposition
Fonctions Paires
Définition. Une fonction \( f : X \to Y \) est dite paire si :
\[ \forall x \in X, \quad -x \in X \quad \text{et} \quad f(-x) = f(x) \]
En d'autres termes, la fonction est paire si le domaine est symétrique par rapport à l'origine et la fonction prend la même valeur en \( x \) et \( -x \).
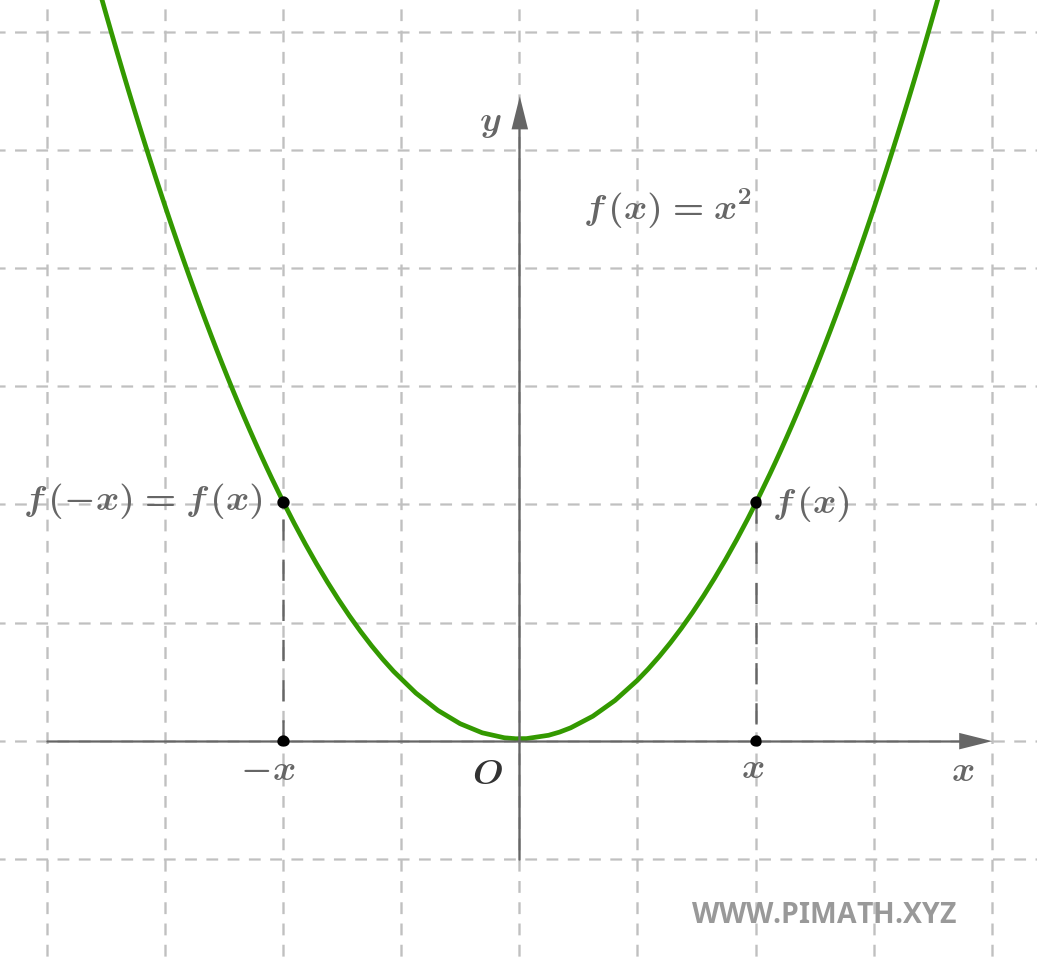
Exemple. La fonction \( f(x) = x^2 \) est paire, en effet pour tout \( x \in \mathbb{R} \), on a \( (-x)^2 = x^2 \).
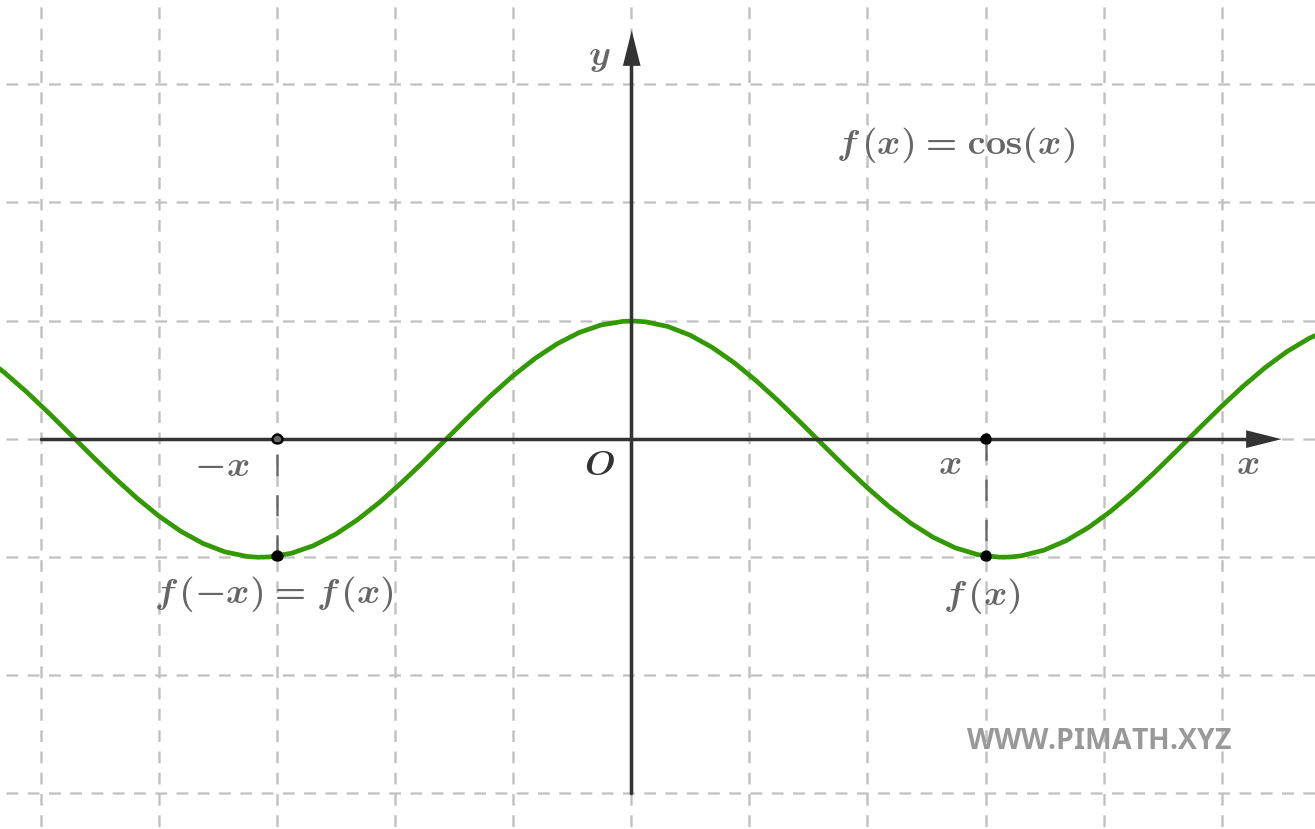
Exemple. La fonction \( f(x) = \cos(x) \) est paire, en effet pour tout \( x \in \mathbb{R} \), on a \( \cos(-x) = \cos(x) \).
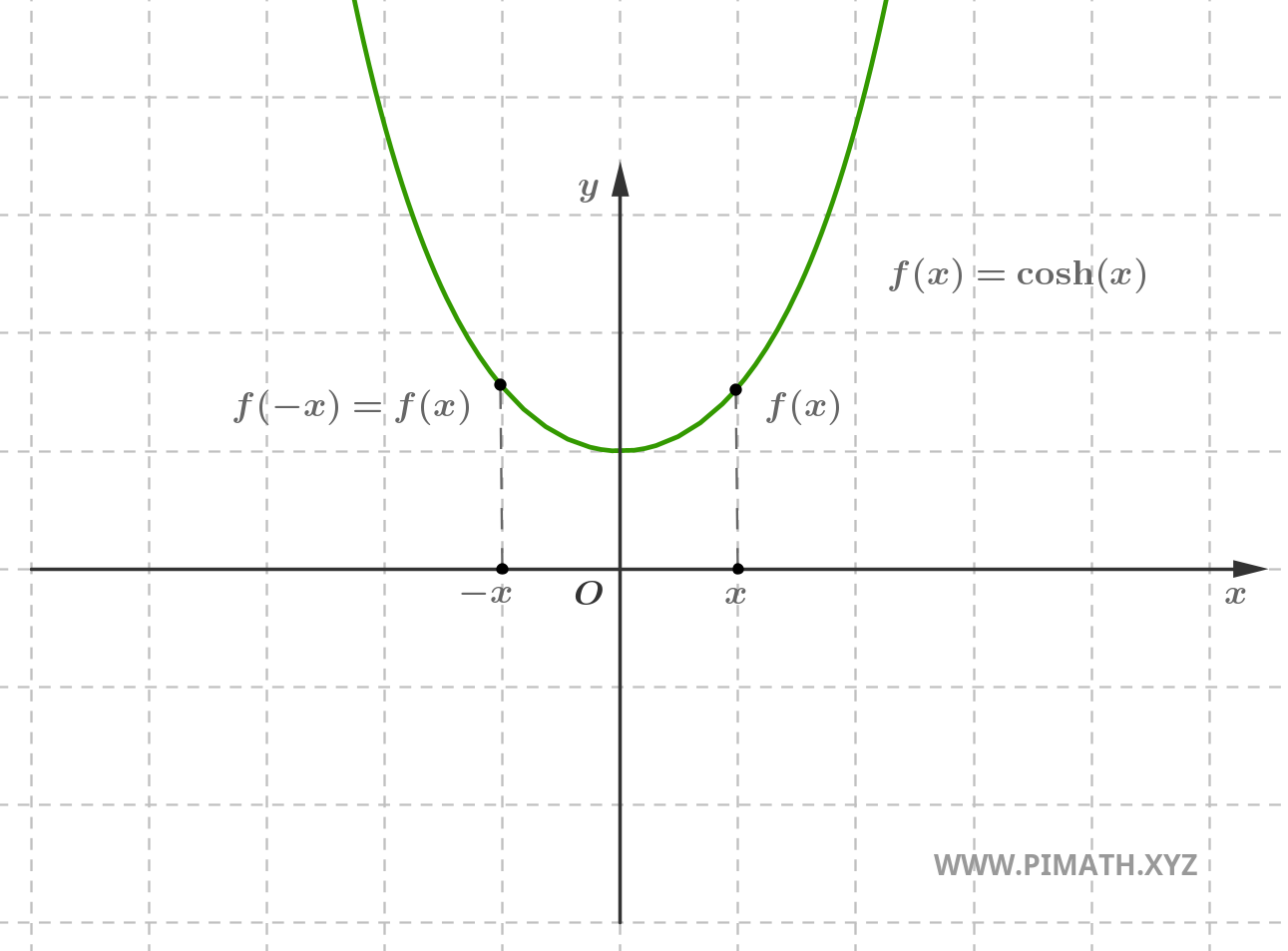
Exemple. La fonction \( f(x) = \cosh(x) \) est paire, en effet pour tout \( x \in \mathbb{R} \), on a \( \cosh(-x) = \cosh(x) \).
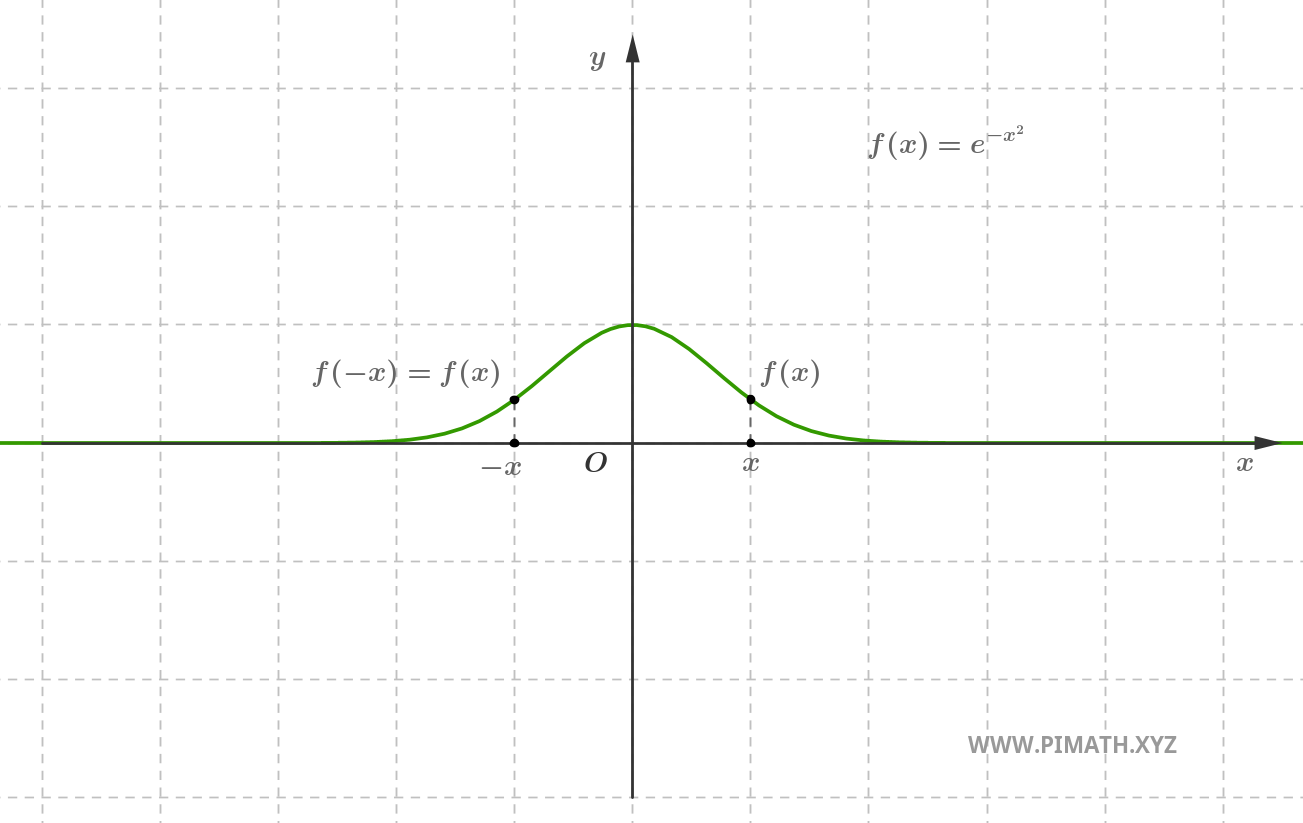
Exemple. La fonction \( f(x) = e^{-x^2} \) est paire, en effet pour tout \( x \in \mathbb{R} \), on a \( e^{-(-x)^2} = e^{-x^2} \).
Somme de deux fonctions paires
Soient \( f \) et \( g \) deux fonctions paires, définies respectivement sur \( D_f \) et \( D_g \). Considérons la fonction somme \( f + g \), définie sur le domaine \( D = D_f \cap D_g \). Puisque \( D_f \) et \( D_g \) sont symétriques, l'intersection \( D \) est également symétrique. Pour tout \( x \in D \), nous avons :
\[ (f + g)(-x) = f(-x) + g(-x) = f(x) + g(x) = (f + g)(x) \]
donc \( f + g \) est une fonction paire.
Une fonction paire présente une symétrie par rapport à l'axe des ordonnées. Par conséquent, pour analyser son graphique, il suffit de l'étudier pour \( x \geq 0 \) ; la partie pour \( x < 0 \) s'obtient par symétrie.
Fonctions Impaires
Définition. Une fonction \( f : X \to Y \) est dite impaire si :
\[ \forall x \in X, \quad -x \in X \quad \text{et} \quad f(-x) = -f(x) \]
En d'autres termes, la fonction est impaire si le domaine est symétrique par rapport à l'origine et la fonction prend des valeurs opposées en \( x \) et \( -x \).
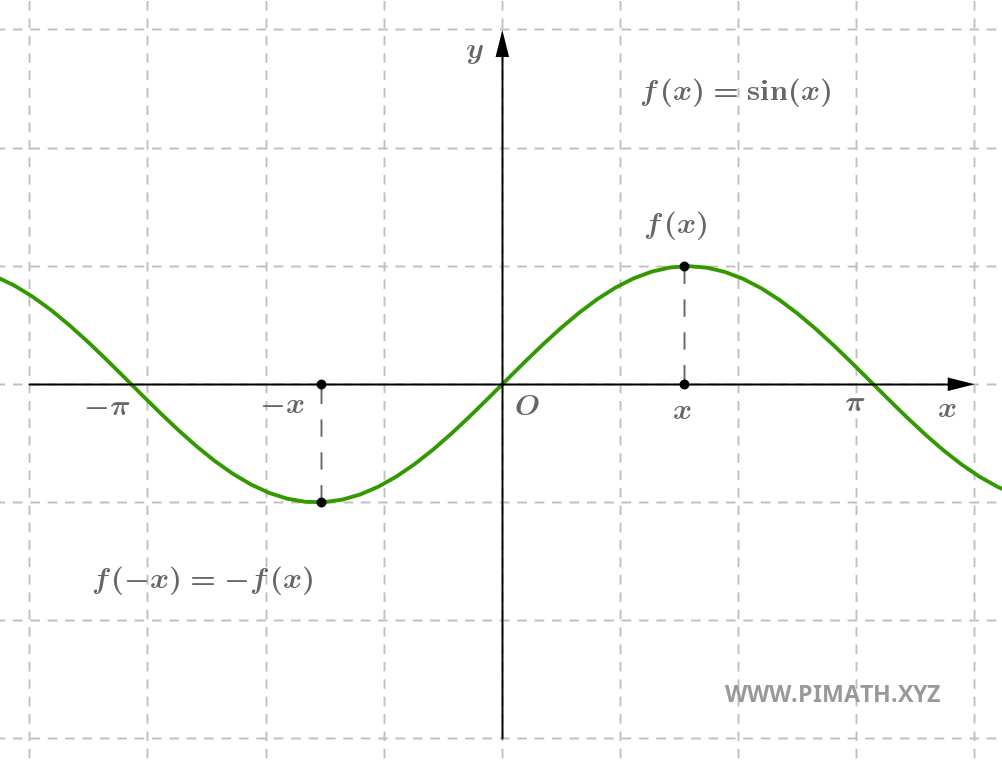
Exemple. La fonction \( f(x) = \sin(x) \) est impaire, en effet pour tout \( x \in \mathbb{R} \), on a \( \sin(-x) = -\sin(x) \).
Exemple. La fonction \( f(x) = x^3 \) est impaire, en effet pour tout \( x \in \mathbb{R} \), on a \( (-x)^3 = -x^3 \).
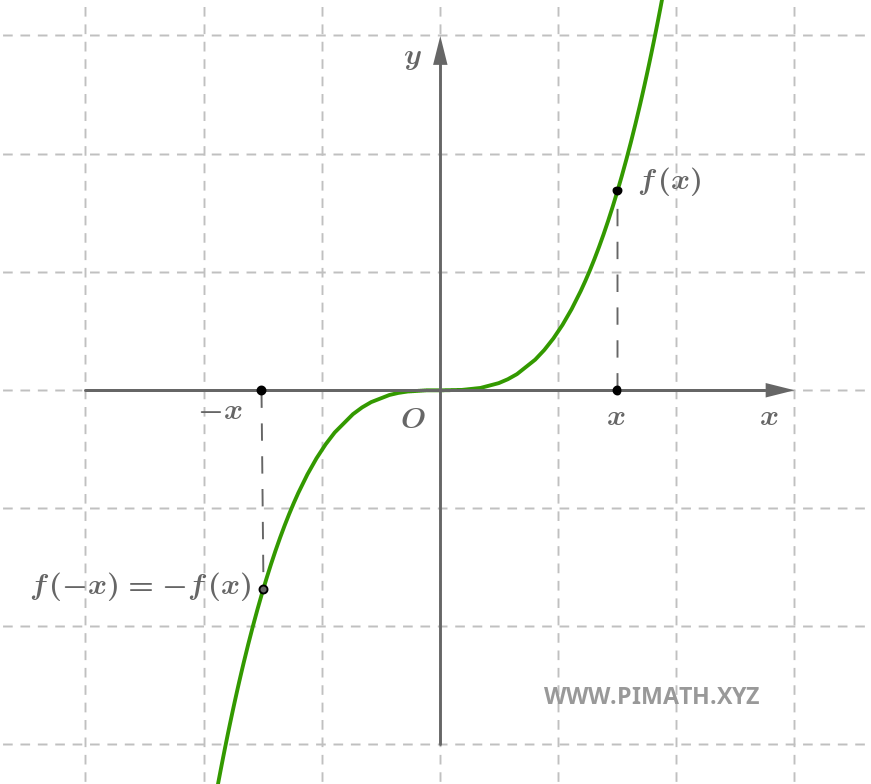
Une fonction impaire est symétrique par rapport à l'origine : en effectuant une rotation de 180° de son graphique autour de l'origine, on obtient le même graphique.
Somme de deux fonctions impaires
Soient \( f \) et \( g \) deux fonctions impaires, définies sur les domaines \( D_f \) et \( D_g \). Alors la somme \( f + g \), définie sur le domaine commun \( D = D_f \cap D_g \), est également impaire.
En effet, pour tout \( x \in D \), on a :
\[ (f + g)(-x) = f(-x) + g(-x) = -f(x) - g(x) = -(f(x) + g(x)) = -(f + g)(x) \]
Donc \( f + g \) est une fonction impaire.
Fonctions ni paires ni impaires
Si une fonction ne satisfait ni la relation \( f(-x) = f(x) \), ni \( f(-x) = -f(x) \), alors elle n'est ni paire ni impaire.
Exemple. Les fonctions \( f(x) = e^x \) et \( f(x) = x + 1 \) ne sont ni paires ni impaires.
Intégration sur des intervalles symétriques
Les fonctions paires et impaires sont particulièrement utiles dans le calcul d'intégrales définies sur des intervalles symétriques par rapport à l'origine.
Si \( f \) est paire, alors :
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
Si \( f \) est impaire, alors :
\[ \int_{-a}^{a} f(x) \, dx = 0 \]
Décomposition d'une fonction en partie paire et partie impaire
Soit \( f : X \to \mathbb{R} \) une fonction définie sur un ensemble symétrique par rapport à l'origine, c'est-à-dire tel que \( x \in X \implies -x \in X \). Dans ce cas, la fonction \( f \) peut être écrite de manière unique comme somme d'une fonction paire et d'une fonction impaire.
Précisément, on définit :
\[ f_p(x) = \frac{f(x) + f(-x)}{2} \quad \text{(partie paire de \( f \))} \]
\[ f_d(x) = \frac{f(x) - f(-x)}{2} \quad \text{(partie impaire de \( f \))} \]
Il est immédiat de vérifier que \( f_p(-x) = f_p(x) \) et \( f_d(-x) = -f_d(x) \), donc \( f_p \) est paire et \( f_d \) est impaire. De plus, en sommant les deux expressions on obtient :
\[ f(x) = f_p(x) + f_d(x) \]
c'est-à-dire que toute fonction \( f \) (définie sur un ensemble symétrique) peut se décomposer de manière unique en somme d'une fonction paire et d'une fonction impaire.
Exemple. Considérons la fonction \( f(x) = e^x \), définie sur tout \( \mathbb{R} \). La partie paire est :
\[ f_p(x) = \frac{e^x + e^{-x}}{2} = \cosh x \]
tandis que la partie impaire est :
\[ f_d(x) = \frac{e^x - e^{-x}}{2} = \sinh x \]
On a donc la décomposition :
\[ e^x = \cosh x + \sinh x \]
Remarque : La décomposition n'est possible que si le domaine de la fonction est symétrique par rapport à l'origine. De plus, l'écriture \( f = f_p + f_d \) est unique : il existe une seule fonction paire et une seule fonction impaire dont la somme redonne \( f \).
Démonstration de l'unicité de la décomposition
Supposons qu'une fonction \( f : X \to \mathbb{R} \), définie sur un ensemble symétrique par rapport à l'origine, puisse s'écrire de deux manières distinctes comme somme d'une fonction paire et d'une fonction impaire :
\[ f(x) = f_p(x) + f_d(x) = g_p(x) + g_d(x), \]
où \( f_p \), \( g_p \) sont paires et \( f_d \), \( g_d \) sont impaires.
Alors :
\[ f_p(x) - g_p(x) = g_d(x) - f_d(x) \]
Appelons \( h(x) = f_p(x) - g_p(x) = g_d(x) - f_d(x) \). La fonction \( h \) est donc paire (comme différence de deux fonctions paires) et impaire (comme différence de deux fonctions impaires).
Mais si une fonction est simultanément paire et impaire, alors :
\[ h(x) = h(-x) \quad \text{et} \quad h(x) = -h(-x) \implies h(x) = -h(x) \]
c'est-à-dire \( h(x) = 0 \) pour tout \( x \in X \).
Donc \( f_p(x) = g_p(x) \) et \( f_d(x) = g_d(x) \), ce qui démontre l'unicité de la décomposition.

