Le Théorème de Rolle est un résultat fondamental applicable aux fonctions continues et dérivables. Ce théorème établit que, si une fonction \( f \) est continue sur un intervalle fermé \([a,b]\), dérivable sur l'intervalle ouvert \((a,b)\) et prend la même valeur aux extrémités \( f(a) = f(b) \), alors il existe au moins un point intérieur \( \xi \in (a,b) \) où la dérivée de la fonction s'annule, c'est-à-dire \( f'(\xi) = 0 \). Ce résultat a de nombreuses applications, notamment la démonstration du Théorème des Accroissements Finis.
Sommaire
Théorème de Rolle
Soit \( f : [a,b] \to \mathbb{R} \) une fonction continue sur l'intervalle fermé \([a,b]\), dérivable sur l'intervalle ouvert \((a,b)\) et telle que \( f(a) = f(b) \). Alors il existe au moins un point \( \xi \in (a,b) \) tel que : \[ f'(\xi) = 0 \]
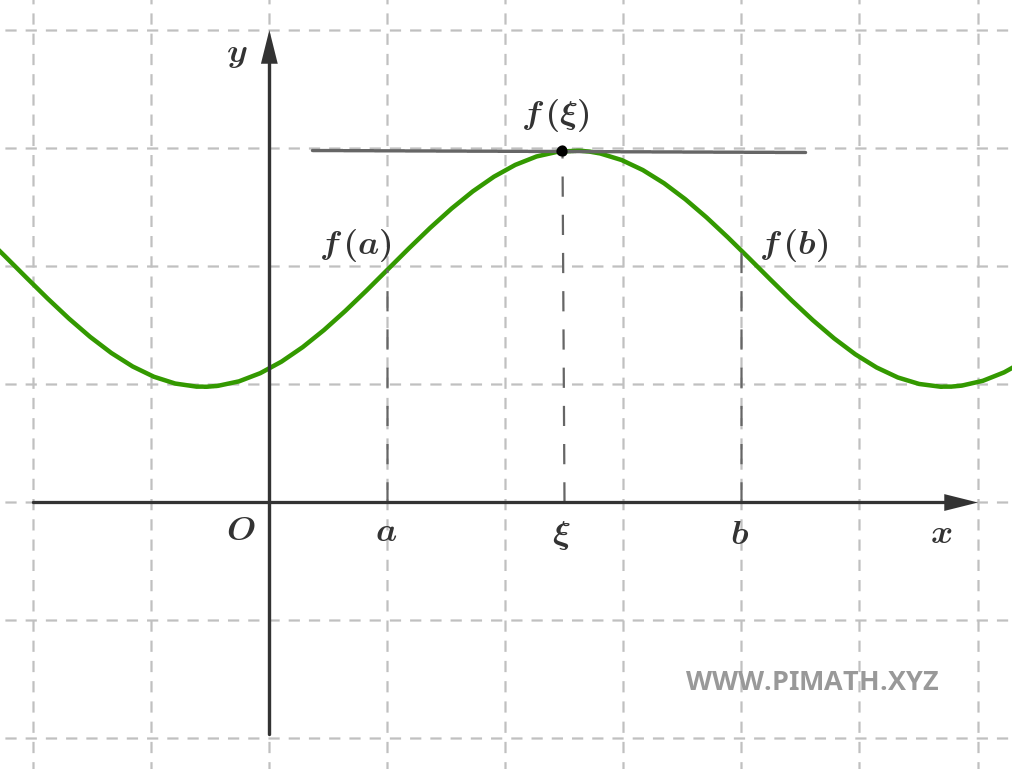
Démonstration. Tout d'abord, puisque \( f \) est continue sur \([a,b]\), d'après le Théorème de Weierstrass, elle admet un maximum et un minimum absolus sur l'intervalle. Par conséquent, il existe des points \( c, d \in [a,b] \) tels que : \[ f(c) = M \quad \text{et} \quad f(d) = m \] où \( M = \max_{x \in [a,b]} f(x) \) et \( m = \min_{x \in [a,b]} f(x) \).
Considérons d'abord le cas où la fonction \( f \) est constante, c'est-à-dire \( f(x) = k \) pour tout \( x \in [a,b] \). Dans ce cas, par définition de la dérivée : \[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{k - k}{h} = 0 \] pour tout \( x \in (a,b) \). La thèse est donc immédiatement vérifiée.
Passons maintenant au cas où \( f \) n'est pas constante. Puisque \( f(a) = f(b) \), le maximum et le minimum absolus ne peuvent pas se trouver tous les deux aux extrémités \( a \) et \( b \). Il doit exister au moins un point \( \xi \in (a,b) \) où \( f(\xi) = M \) ou bien \( f(\xi) = m \). Dans les deux cas, \( \xi \) représente un point de maximum ou de minimum local.
Soit \( \xi \) un point de maximum local. Pour \( h \) suffisamment petit :
\[ f(\xi + h) \leq f(\xi) \]
Nous pouvons alors considérer les taux d'accroissement :
\[ \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \quad \text{si} \ h > 0 \]
\[ \frac{f(\xi + h) - f(\xi)}{h} \geq 0 \quad \text{si} \ h < 0 \]
Étant donné que \( f \) est dérivable en \( \xi \), la limite du taux d'accroissement existe, c'est-à-dire : \[ f'(\xi) = \lim_{h \to 0} \frac{f(\xi + h) - f(\xi)}{h} \]
D'après ce qui précède, nous avons :
\[ \lim_{h \to 0^+} \frac{f(\xi + h) - f(\xi)}{h} \leq 0 \leq \lim_{h \to 0^-} \frac{f(\xi + h) - f(\xi)}{h} \]
Donc, nécessairement : \[ f'(\xi) = 0 \]
Un raisonnement analogue s'applique dans le cas où \( \xi \) est un point de minimum local.
Nous avons ainsi démontré qu'il existe au moins un point \( \xi \in (a,b) \) tel que \( f'(\xi) = 0 \), achevant la démonstration du Théorème de Rolle.

