Une équation du premier degré est un polynôme du premier degré égalé à zéro. En général, une équation est du premier degré si elle peut être écrite sous la forme canonique :
\[ ax + b = 0 \quad \text{avec} \quad a \neq 0 \]
La partie qui se trouve à gauche du signe d'égalité prend le nom de premier membre, tandis que celle qui se trouve à droite prend le nom de second membre.
Sommaire
- Comment résoudre une équation du premier degré
- Premier principe d'équivalence
- Second principe d'équivalence
- Exercices Résolus
- Erreurs courantes à éviter
- Signification Géométrique
Comment résoudre une équation du premier degré
Résoudre une équation du premier degré signifie trouver la valeur qui, substituée à l'inconnue \( x \), satisfait l'équation. Cela équivaut à dire que la valeur (solution de l'équation) doit rendre vraie l'égalité. Le processus de résolution comprend certaines étapes, appelées principes d'équivalence pour les équations.
Premier principe d'équivalence
Le premier principe d'équivalence énonce qu'en ajoutant ou en soustrayant aux deux membres d'une équation une quantité ou une expression algébrique, l'ensemble des solutions ne change pas.
Grâce à ce principe, nous pouvons soustraire la quantité \( -b \) aux deux membres :
\[ ax = -b \]
Remarquez qu'ajouter ou soustraire une quantité aux deux membres équivaut à « faire passer » d'un membre à l'autre pourvu que le signe soit changé. Pour l'instant, nous avons fait passer au second membre \( b \) en changeant son signe, donc \( -b \).
Second principe d'équivalence
Le second principe d'équivalence énonce qu'en multipliant ou en divisant par un même nombre différent de zéro, l'ensemble des solutions de l'équation ne change pas.
En appliquant ce principe à l'équation équivalente \( ax = -b \), donc en divisant par le nombre \( a \neq 0 \) aux deux membres, nous obtenons :
\[ x = -\frac{b}{a} \]
Il est important de souligner que \( a \) doit être différent de zéro pour que l'équation ait un sens. En effet, si \( a = 0 \) l'équation deviendrait \( 0 \cdot x + b = 0 \) et donc \( b = 0 \), ce qui ne représente pas une équation en \( x \) et serait impossible si \( b \neq 0 \).
Désormais, l'objectif sera d'isoler la variable \( x \) au premier membre, ou au second (cela ne change rien).
Exercices Résolus
Exercice 1. Résoudre l'équation \( 3x - 1 = 0\).
Solution. Nous faisons passer \( -1 \) au second membre (en changeant son signe) :
\[ 3x = 1 \]
Enfin, en divisant les deux membres par \( 3 \) nous obtenons la solution recherchée :
\[ x = \frac{1}{3} \]
Vérification. Pour vérifier que c'est la solution correcte, nous substituons la valeur trouvée dans l'équation de départ. Nous obtenons :
\[ 3 \cdot \frac{1}{3} - 1 = 1 - 1 = 0 \]
Par conséquent, la solution est correcte.
Exercice 2 : Résoudre l'équation du premier degré \(\displaystyle\frac{1}{2}(x-1)=-x+1\).
Solution. Nous commençons par isoler l'inconnue \( x \) au premier membre :
\[ \frac{1}{2}(x - 1) = -x + 1 \implies \frac{x}{2} - \frac{1}{2} = -x + 1 \]
Maintenant nous ajoutons \(x\) aux deux membres de l'équation :
\[ \frac{x}{2} + x - \frac{1}{2} = 1 \]
Nous simplifions en transformant \(x\) en un terme avec un dénominateur commun :
\[ \frac{x}{2} + \frac{2x}{2} - \frac{1}{2} = 1 \implies \frac{3x}{2} - \frac{1}{2} = 1 \]
Nous ajoutons \(\displaystyle\frac{1}{2}\) aux deux membres :
\[ \frac{3x}{2} = \frac{3}{2} \]
Maintenant nous multiplions les deux membres par \(\displaystyle\frac{2}{3}\) pour résoudre pour \(x\) :
\[ x = 1 \]
Par conséquent, la solution est \( x = 1 \).
Vérification. Comme précédemment, nous substituons \( x = 1 \) dans l'équation de départ :
\[ \frac{1}{2}(x - 1) = -x + 1 \]
Quand \( x = 1 \), nous obtenons :
\[ \frac{1}{2}(1 - 1) = -1 + 1 \]
Nous calculons les deux membres :
\[ \frac{1}{2} \cdot 0 = 0 \quad \text{et} \quad -1 + 1 = 0 \]
Les deux membres sont égaux, donc la solution est correcte.
Exercice 3. Résoudre l'équation \( 5(x - 2) - 3(2x + 1) = 7 - 4x \)
Solution. Nous appliquons la propriété distributive :
\[ 5x - 10 - 6x - 3 = 7 - 4x \]
\[ -x - 13 = 7 - 4x \]
Nous faisons passer les termes avec \(x\) au premier membre et les termes constants au second membre :
\[ -x + 4x = 7 + 13 \]
\[ 3x = 20 \]
Nous divisons les deux membres par 3 :
\[ x = \frac{20}{3} \]
Vérification. Nous substituons \(\displaystyle x = \frac{20}{3}\) dans l'équation de départ :
\[ 5\left(\frac{20}{3} - 2\right) - 3\left(2\cdot\frac{20}{3} + 1\right) = 7 - 4\cdot\frac{20}{3} \]
Nous calculons le premier membre :
\[ 5\left(\frac{20}{3} - \frac{6}{3}\right) - 3\left(\frac{40}{3} + \frac{3}{3}\right) = 5\cdot\frac{14}{3} - 3\cdot\frac{43}{3} = \frac{70}{3} - \frac{129}{3} = -\frac{59}{3} \]
Nous calculons le second membre :
\[ 7 - 4\cdot\frac{20}{3} = \frac{21}{3} - \frac{80}{3} = -\frac{59}{3} \]
Les deux membres sont égaux, donc la solution est vérifiée :
\[ x = \frac{20}{3} \]
Erreurs courantes à éviter
Lorsqu'on résout des équations du premier degré, il est important de faire attention à quelques erreurs fréquentes :
Erreur dans le changement de signe : Quand on fait passer un terme d'un membre à l'autre, il faut se rappeler de changer son signe. Par exemple, dans l'équation \(2x + 3 = 5\), en faisant passer le \( 3 \) on obtient \(2x = 5 - 3\) et non \(2x = 5 + 3\).
Distribution incomplète : Quand on a une expression du type \(3(x + 2)\), le coefficient \( 3 \) doit être multiplié par tous les termes à l'intérieur des parenthèses. Une erreur commune est d'écrire \(3x + 2\) au lieu du correct \(3x + 6\).
Erreurs avec les fractions : Quand on a une équation comme \(\displaystyle \frac{x}{2} = 3\), pour isoler \(x\) il faut multiplier les deux membres par 2, en obtenant \(x = 6\). Il est incorrect d'écrire \(x = \displaystyle \frac{3}{2}\).
Simplification imprécise : Dans une équation comme \(2x - x = 5\), il ne faut pas oublier de simplifier les termes semblables avant de procéder. La forme correcte est \(x = 5\).
Vérification manquante : Sauter l'étape de la vérification peut conduire à ne pas s'apercevoir d'éventuelles erreurs de calcul. Il est toujours conseillable de substituer la solution trouvée dans l'équation originale pour confirmer qu'elle soit correcte.
Signification Géométrique
Résoudre une équation du premier degré \( ax + b = 0\) signifie trouver la valeur en correspondance de laquelle la droite d'équation
\[ y = ax + b \]
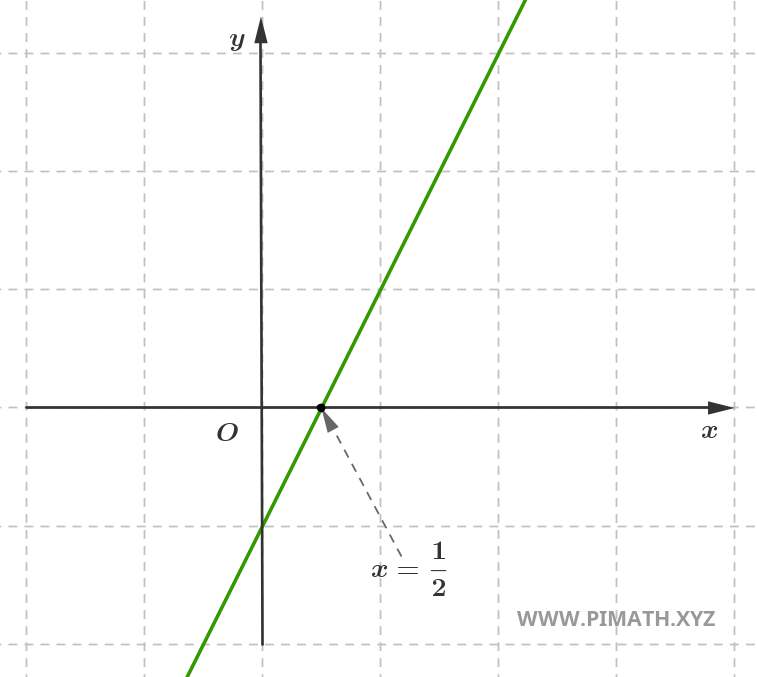
coupe l'axe des abscisses (axe \( x \)). Par exemple, la droite d'équation \( y = 2x - 1 \)
coupe l'axe des abscisses au point \( x = \displaystyle \frac{1}{2} \), comme montré dans la figure.
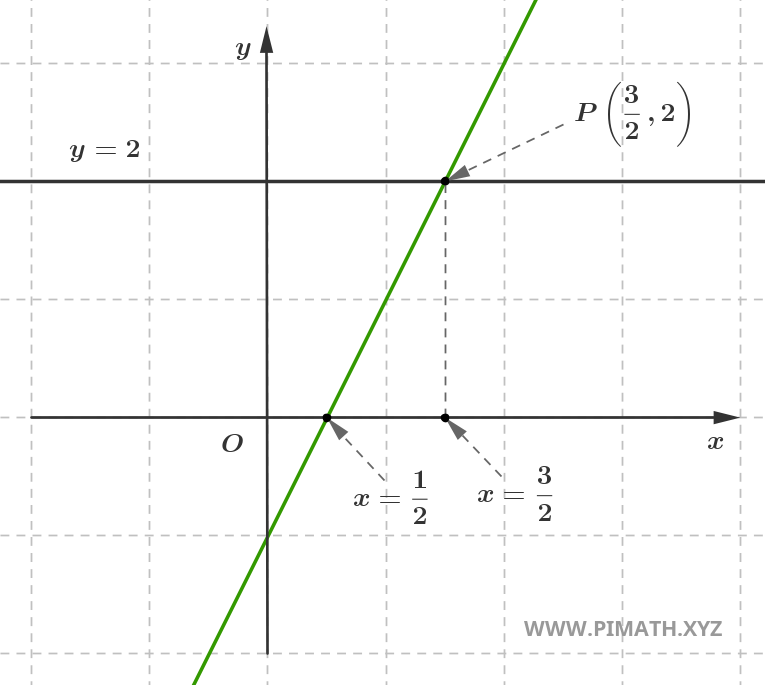
Nous avons dit que la solution d'une équation du premier degré \( ax + b = 0 \) est l'abscisse en laquelle la droite coupe l'axe \(x\). Maintenant, posons-nous une autre question : comment pouvons-nous déterminer la valeur de \( x \) pour laquelle la droite \( y = ax + b \) prend une valeur spécifique, par exemple \( y = 2 \) ?
Pour faire cela, il suffit d'imposer \( y = 2 \) dans l'équation de la droite. Nous obtenons ainsi \( 2 = 2x - 1 \iff 2x - 3 = 0 \), donc :
\[ x=\frac{3}{2} \]
Comme montré dans la figure, à la solution que nous avons trouvée correspond l'ordonnée \(y=2\).