Les limites remarquables sont des expressions fondamentales en analyse mathématique qui décrivent le comportement local des fonctions en des points critiques.
Ces limites sont des outils essentiels pour établir la continuité, la dérivabilité et pour simplifier l'analyse du comportement asymptotique de fonctions plus complexes.
- Démonstration par le Critère de Comparaison
- Démonstration par la règle de De L'Hôpital
- Démonstration par le développement en série de Taylor
Démonstration par le Critère de Comparaison
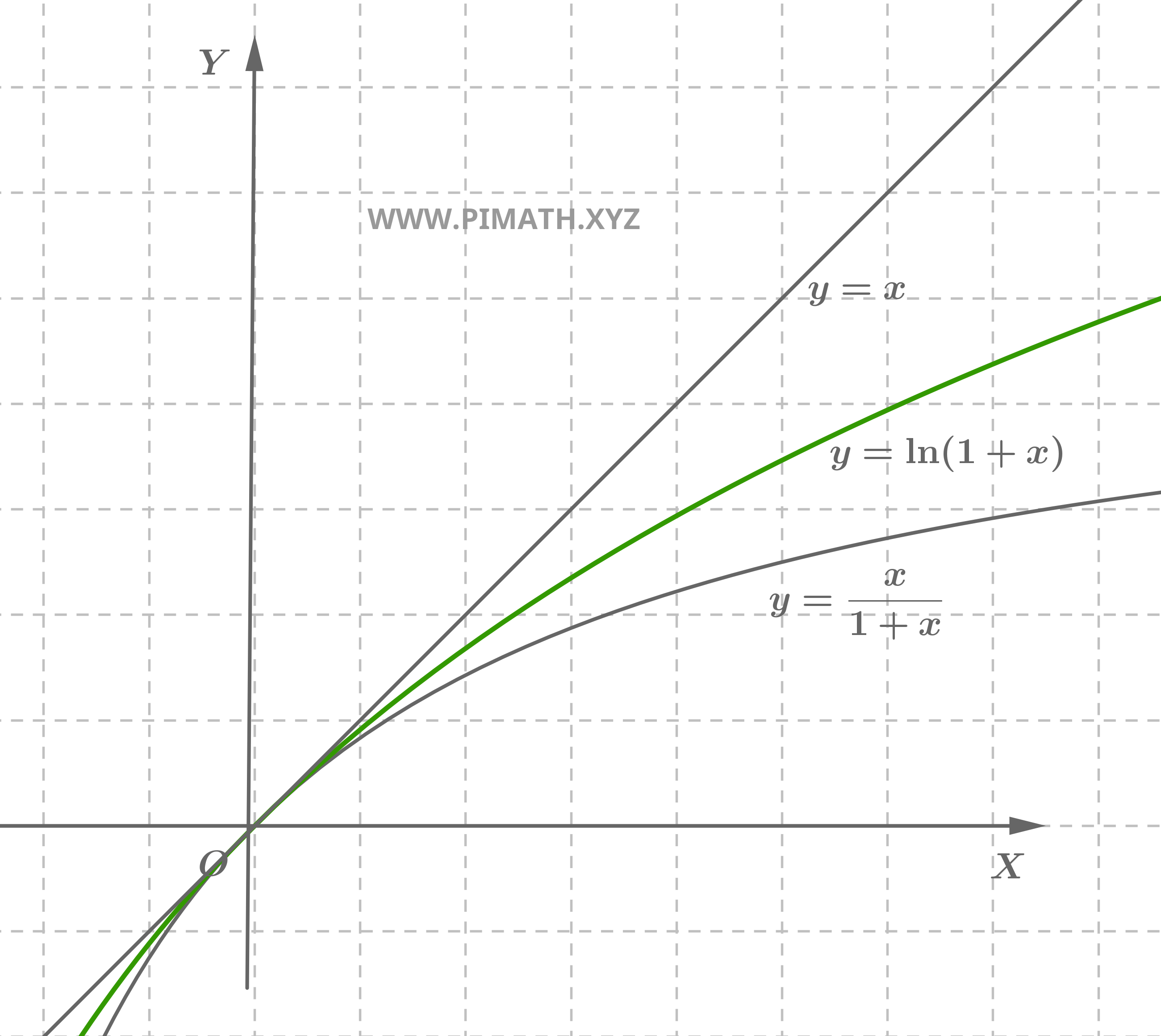
Considérons la limite \[ \lim_{x \to 0} \frac{\ln(1+x)}{x}. \] Pour \( x > 0 \) nous pouvons utiliser les propriétés de concavité de la fonction \(\ln(1+x)\). En particulier, sachant que la fonction est concave, il en résulte que le graphe de \(\ln(1+x)\) se trouve en dessous de la tangente en \( x=0 \), c'est-à-dire : \[ \ln(1+x) \leq x. \]
De plus, il peut être démontré que pour \( x > 0 \) la relation suivante est également vraie : \[ \ln(1+x) \geq \frac{x}{1+x}. \] Ces inégalités se résument ainsi :\[ \frac{x}{1+x} \leq \ln(1+x) \leq x \]
En divisant par \( x \) (pour \( x > 0 \)), nous obtenons : \[ \frac{1}{1+x} \leq \frac{\ln(1+x)}{x} \leq 1 \]
Calculons maintenant les limites des bornes lorsque \( x \to 0 \) : \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1 \quad \text{et} \quad \lim_{x \to 0} 1 = 1. \] Par le théorème des gendarmes, il s'ensuit que : \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Par conséquent, nous avons démontré par comparaison que : \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
Dans ce document, nous démontrons la limite remarquable suivante :
Démonstration par la règle de De L'Hôpital
On observe que, en posant \( f(x) = \ln(1+x) \) et \( g(x) = x \), lorsque \( x \) tend vers zéro, nous avons \[ f(0) = \ln(1+0) = 0 \quad \text{et} \quad g(0) = 0, \] de sorte que la limite prend la forme indéterminée \(\frac{0}{0}\). Cette condition nous permet d'appliquer la règle de De L'Hôpital.
Nous dérivons donc le numérateur et le dénominateur :
\[ f'(x) = \frac{d}{dx}\ln(1+x) = \frac{1}{1+x}, \quad g'(x) = \frac{d}{dx}x = 1 \]
En appliquant la règle de De L'Hôpital, nous obtenons : \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} = \lim_{x \to 0} \frac{1}{1+x} \]
Comme la limite \(\lim_{x \to 0} \frac{1}{1+x}\) est immédiatement calculable, nous avons : \[ \lim_{x \to 0} \frac{1}{1+x} = \frac{1}{1+0} = 1 \]
Par conséquent, il s'ensuit que : \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
Démonstration par le développement en série de Taylor
Alternativement, nous pouvons démontrer le résultat en recourant au développement en série de Taylor de la fonction \(\ln(1+x)\) autour de \( x=0 \) :
La série de Taylor de \(\ln(1+x)\) est donnée par : \[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots, \quad \text{pour } |x| < 1. \]
En divisant par \( x \), on obtient : \[ \frac{\ln(1+x)}{x} = 1 - \frac{x}{2} + \frac{x^2}{3} - \cdots. \]
En faisant tendre \( x \) vers zéro, tous les termes contenant des puissances positives de \( x \) disparaissent, ce qui donne : \[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1. \]
Nous avons ainsi démontré, par trois méthodes, que :
\[ \lim_{x \to 0} \frac{\ln(1+x)}{x} = 1 \]
La première démonstration a utilisé le critère de comparaison, la deuxième la règle de De L'Hôpital, tandis que la troisième s'est basée sur le développement en série de Taylor.

