Una disequazione di secondo grado è un'espressione algebrica che stabilisce una relazione d'ordine tra due termini contenenti una variabile di secondo grado. Può essere scritta nella forma:
\[ a x^2 + bx + c \leq 0 \quad \text{oppure} \quad a x^2 + bx + c \geq 0 \]
dove \( a \) e \( b \) sono coefficienti reali con \( a \neq 0 \) e \( x \) è la variabile incognita. Si parla di disequazione in senso stretto se
\[ a x^2 + bx + c < 0 \quad \text{oppure} \quad a x^2 + bx + c > 0 \]
- Cosa sono le Disequazioni di Secondo Grado
- Principi di Equivalenza per le Disequazioni
- Come risolvere le Disequazioni di Secondo Grado
Cosa sono le Disequazioni di Secondo Grado
Una disequazione di secondo grado stabilisce una relazione d'ordine tra due espressioni algebriche, e la soluzione è rappresentata da un intervallo di valori che verificano la disuguaglianza. In altre parole, l'insieme delle soluzioni di una disequazione di secondo grado non sono due, ma un intervallo o l'unione di intervalli di numeri reali.
Principi di Equivalenza per le Disequazioni di Secondo Grado
La risoluzione di una disequazione di secondo grado si basa su due principi fondamentali:
Primo Principio di Equivalenza
Il principio di equivalenza per le disequazioni di secondo grado afferma che se si aggiunge o sottrae lo stesso numero a entrambi i membri di una disequazione, la relazione di ordine non cambia. Ad esempio:
Se \( a x^2 + b x + c \leq 0 \), allora possiamo aggiungere \( d \) a entrambi i membri e ottenere:
\[ (a x^2 + b x + c) + d \leq 0 + d \]
Secondo Principio di Equivalenza
Il secondo principio di equivalenza afferma che se si moltiplica o divide entrambi i membri di una disequazione per un numero positivo, la relazione di ordine non cambia. Tuttavia, se si moltiplica o divide per un numero negativo, la disequazione deve essere invertita. Ecco alcuni esempi:
Se \( a x^2 + b x + c \leq 0 \) e moltiplichiamo entrambi i membri per un numero positivo \( k \), otteniamo:
\[ k(a x^2 + b x + c) \leq k \cdot 0 \]
Se, invece, moltiplichiamo per un numero negativo \( k \), la disequazione diventa:
\[ k(a x^2 + b x + c) \geq k \cdot 0 \]
Quando si moltiplica o si divide entrambi i membri di una disequazione di secondo grado per un numero negativo, bisogna invertire il segno della disequazione. Ad esempio:
Se \( -2 x^2 + 4 x \leq 6 \), dividendo entrambi i membri per \( -2 \), dobbiamo invertire il segno della disequazione:
\[ x^2 - 2 x \geq -3 \]
Come risolvere le Disequazioni di Secondo Grado
Il primo passo è quello di riscrivere la disequazione in forma canonica, dunque portiamo al primo membro tutti i termini:
\[ ax^2+bx+c \leq 0 \quad \text{oppure} \quad ax^2+bx+c \geq 0 \]
\[ ax^2+bx+c < 0 \quad \text{oppure} \quad ax^2+bx+c > 0 \]
a seconda che si tratti di una disuguaglianza o disuguaglianza in senso stretto.
A questo punto, dobbiamo calcolare le radici (o soluzioni) dell'equazione associata, utilizzando la formula risolutiva per le equazioni di secondo grado:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a}, \quad \text{con} \quad \Delta = b^2 - 4ac \]
Le soluzioni ottenute ci permetteranno di determinare gli intervalli in cui la disequazione è verificata, ossia i valori di \(x\) per i quali la disequazione è soddisfatta, sia entro che oltre tali intervalli.
Il segno del discriminante \( \Delta \) ci consente di comprendere la natura delle soluzioni: se \( \Delta > 0 \), ci sono due soluzioni reali distinte; se \( \Delta = 0 \), ci sono due soluzioni reali e coincidenti; se \( \Delta < 0 \), non ci sono soluzioni reali.
Risoluzione della disequazione:
Se il coefficiente quadratico dell'equazione associata è maggiore di zero, allora le soluzioni saranno:
- \( (x_1, x_2) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c < 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1) \cup (x_2, +\infty) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c > 0 \quad , \quad a > 0 \]
- \( [x_1, x_2] \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c \leq 0 \quad , \quad a > 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c \geq 0 \quad , \quad a > 0 \]
Nel caso in cui il coefficiente quadratico sia negativo (\(a < 0\)), gli intervalli di soluzione saranno invertiti:
- \( (-\infty, x_1) \cup (x_2, +\infty) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c < 0 \quad , \quad a < 0 \]
- \( (x_1, x_2) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c > 0 \quad , \quad a < 0 \]
- \( (-\infty, x_1] \cup [x_2, +\infty) \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c \leq 0 \quad , \quad a < 0 \]
- \( [x_1, x_2] \) se la disequazione che vogliamo studiare è
\[ ax^2+bx+c \geq 0 \quad , \quad a < 0 \]
Come vedremo nella sezione dedicata alla rappresentazione grafica, non avrai bisogno di imparare queste regole a memoria.
Esempi Pratici con Spiegazioni Passo-Passo
Vediamo alcuni esempi di risoluzione di una disequazione di secondo grado.
Esercizio 1. Trova i valori per i quali la seguente disequazione \( x^2 - 5x \leq -6 \) è vera.
Soluzione. Per risolvere questa disequazione, seguiamo i passaggi fondamentali. Per prima cosa, portiamo tutto al primo membro in modo da ottenere la forma canonica:
\[ x^2 - 5x + 6 \leq 0 \]
Ora calcoliamo il discriminante dell'equazione associata. Considerando l'espressione \( x^2 - 5x + 6 \), otteniamo:
\[ \Delta = (-5)^2 - 4(1)(6) = 25 - 24 = 1 \]
Il discriminante è positivo, quindi l'equazione ha due soluzioni reali distinte. Risolvendo l'equazione associata \( x^2 - 5x + 6 = 0 \), troviamo i valori:
\[ x_{1,2} = \frac{-(-5) \pm \sqrt{1}}{2(1)} = \frac{5 \pm 1}{2} \]
dunque \( x_1 = 2 \) e \( x_2 = 3 \).
Poiché il coefficiente del termine \( x^2 \) è positivo, la parabola ha la concavità rivolta verso l'alto e la disequazione sarà soddisfatta nell'intervallo compreso tra le due soluzioni.
Le soluzioni è \( 2 \leq x \leq 3 \) possono essere graficamente rappresentate come segue:
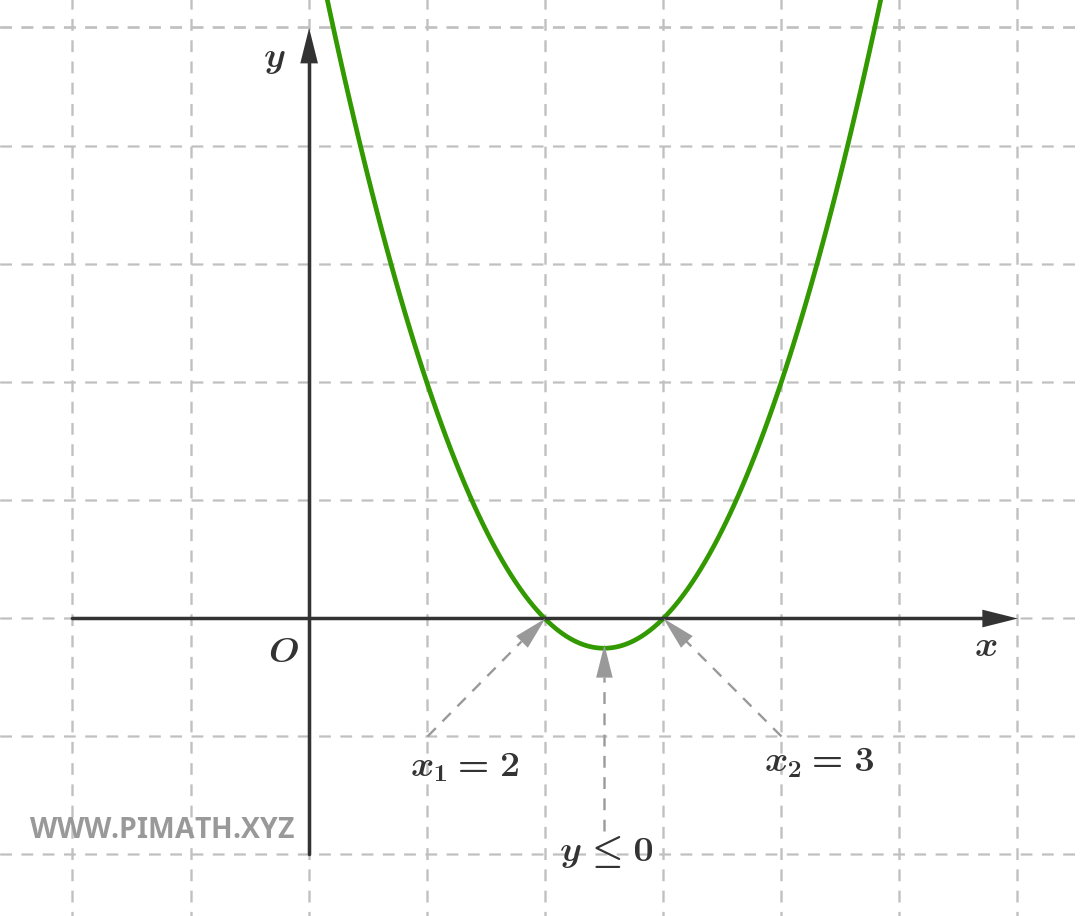
Solitamente, per evitare di disegnare ogni volta la parabola, si preferisce riportare le soluzioni su una retta, distinguendo i valori positivi con una linea continua e negativi con una linea tratteggiata. Ad esempio, le soluzioni della disequazione precedente sono rappresentate in questo modo:
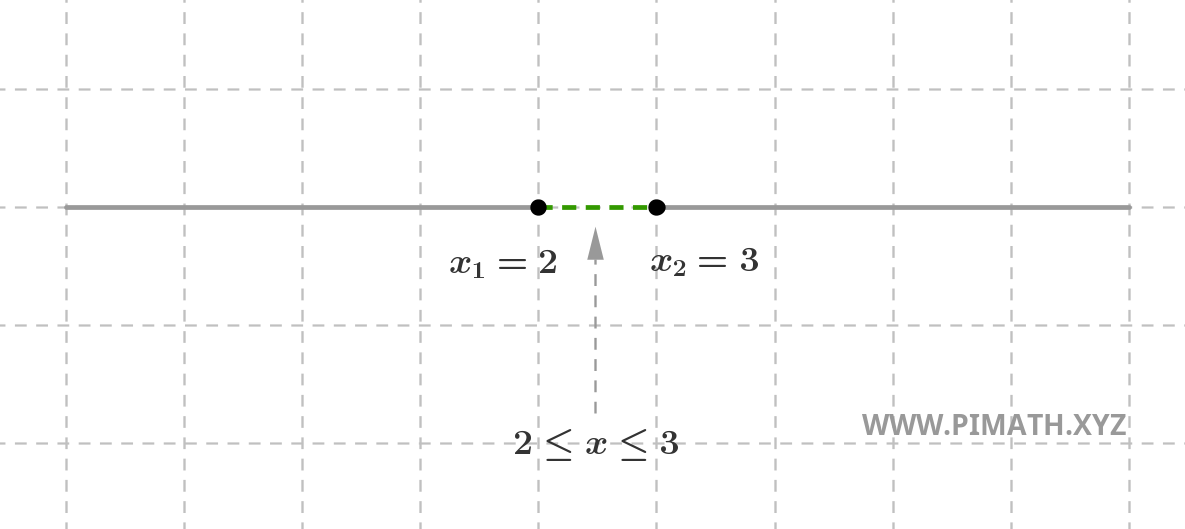
Attenzione all'inclusione delle soluzioni: Se stiamo studiando una disequazione in senso stretto (\( < \) o \( > \)), le radici dell'equazione associata devono essere escluse, e ciò si rappresenta con pallini vuoti nella rappresentazione grafica. Se invece la disequazione è in senso largo (\( \leq \) o \( \geq \)), le radici sono incluse e vengono indicate con pallini pieni.
Esercizio 2. Risolvere la disequazione di secondo grado \( 2x^2 - 4x - 6 > 0 \)
Soluzione. Calcoliamo il discriminante \( \Delta = b^2 - 4ac \)
Per questa equazione, \( a = 2 \), \( b = -4 \), e \( c = -6 \). Sostituendo questi valori nella formula:
\[ \Delta = (-4)^2 - 4(2)(-6) = 16 + 48 = 64 \]
Poiché \( \Delta > 0 \), l'equazione ha due soluzioni reali distinte.
La formula risolutiva per l'equazione associata è:
\[ x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} \]
Sostituendo \( b = -4 \), \( \Delta = 64 \), e \( a = 2 \) nella formula:
\[ x_{1,2} = \frac{4 \pm \sqrt{64}}{2 \times 2} = \frac{4 \pm 8}{4} \]
La prima soluzione è \( x_1 = \displaystyle \frac{4 - 8}{4} = \displaystyle \frac{-4}{4} = -1 \), la seconda soluzione è invece \( x_2 = \displaystyle \frac{4 + 8}{4} = \displaystyle \frac{12}{4} = 3 \).
Le soluzioni dell'equazione sono quindi:
\[ x_1 = -1 \quad \text{e} \quad x_2 = 3 \]
Nota che il coefficiente quadratico è maggiore di zero e la disequazione chiede le soluzioni per le quali si ha \( ax^2+bx+c > 0 \), dunque le soluzioni positive si trovano "esterne all'intervallo", cioè \( x < -1 \) oppure \( x > 3 \), come mostra il grafico:
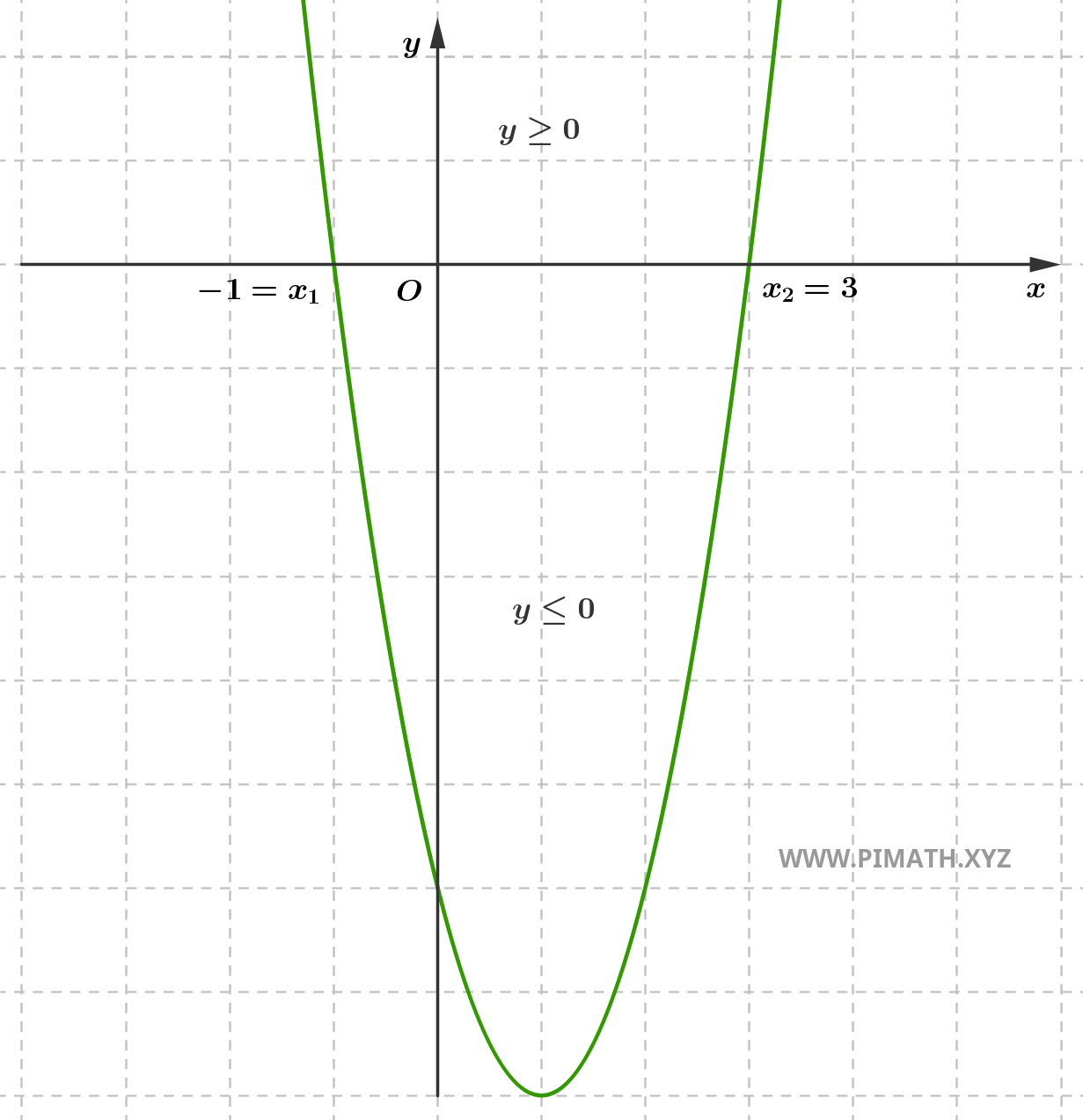
Oppure:
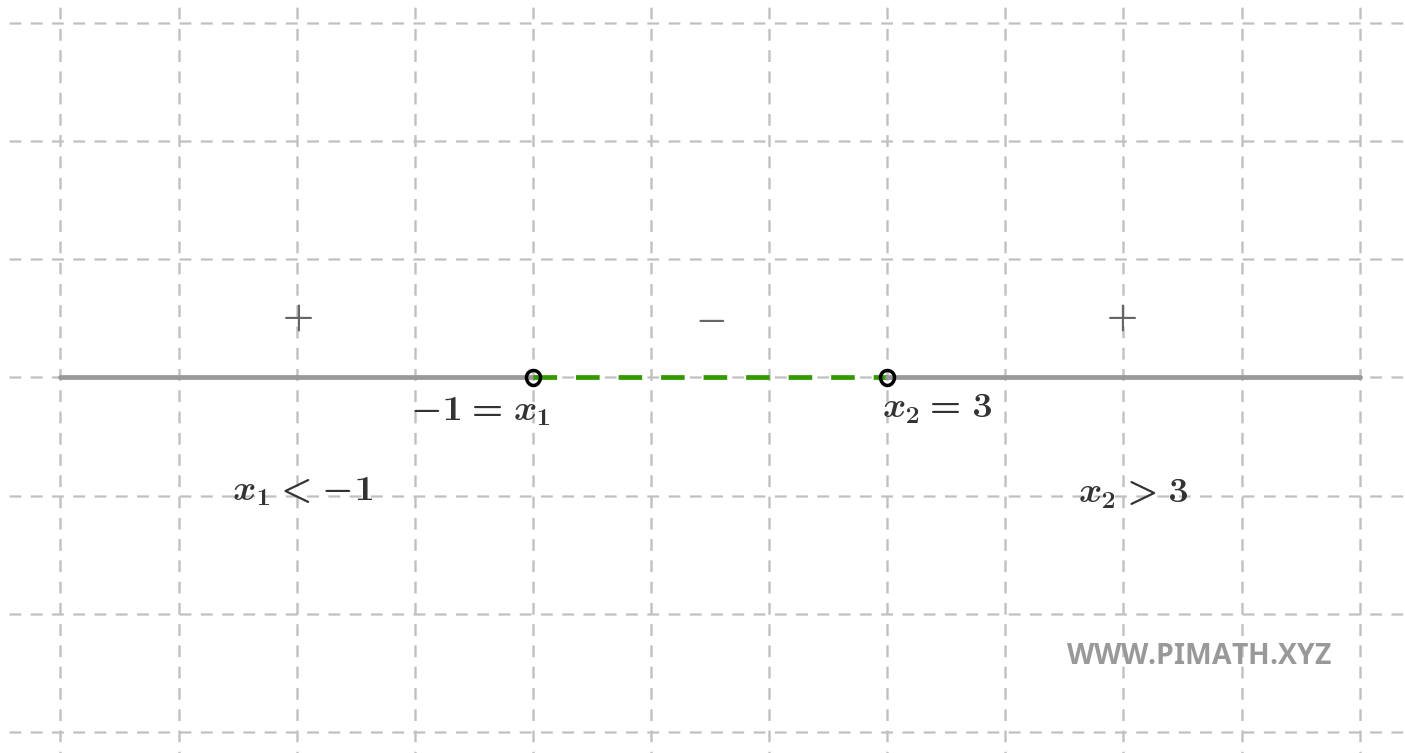
Osserva, infine, che i pallini non sono pieni in quanto stiamo escludendo i punti \( x = -1 \) e \( x = 3 \).
Esercizio 3. Risolvere la disequazione di secondo grado \( 2x^2+x+1 \leq 0 \).
Soluzione. La disequazione si presenta già in forma canonica.
Calcoliamo il discriminante:
\[ \Delta = b^2 - 4ac \]
Sostituendo \( a = 2 \), \( b = 1 \), \( c = 1 \):
\[ \Delta = (1)^2 - 4(2)(1) = 1 - 8 = -7 \]
Poiché il discriminante è negativo, l'equazione associata \( 2x^2+x+1 = 0 \) non ha soluzioni reali.
Inoltre, poiché il coefficiente del termine quadratico è positivo (\( a = 2 > 0 \)), la parabola ha la concavità rivolta verso l'alto, il che significa che il suo valore è sempre positivo per ogni valore di \( x \).
Per una disequazione nella forma \( 2x^2+x+1 \leq 0 \) con \( a > 0 \) e discriminante negativo, la disequazione non ha soluzioni, poiché la funzione è sempre positiva e non può mai essere minore o uguale a zero.
Quindi, la soluzione è l'insieme vuoto. Il grafico della funzione è:
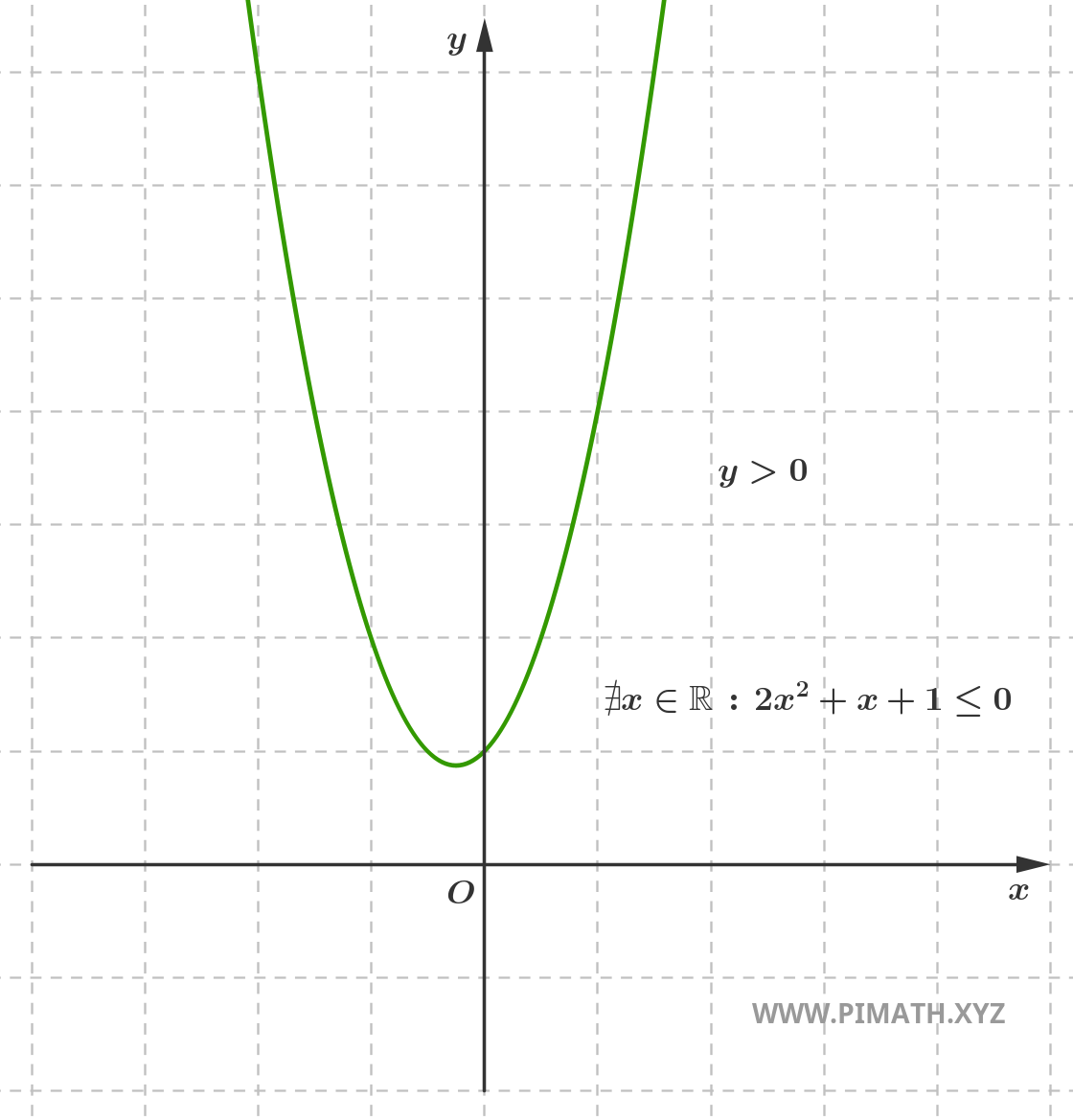
Come si può osservare, la parabola è sempre al di sopra dell'asse \( x \), quindi non ci sono valori di \( x \) che soddisfano la disequazione \( 2x^2+x+1 \leq 0 \).

