Le funzioni pari e funzioni dispari si distinguono per le loro simmetrie: le funzioni pari sono simmetriche rispetto all’asse delle ordinate, mentre le funzioni dispari lo sono rispetto all’origine. Approfondiremo anche il comportamento della somma di funzioni: la somma di due funzioni pari è ancora una funzione pari, così come la somma di due funzioni dispari è ancora dispari. Infine, vedremo come decomporre una funzione nella sua parte pari e nella sua parte dispari.
- Funzioni Pari
- Somma di due funzioni pari
- Funzioni Dispari
- Somma di due funzioni dispari
- Funzioni né pari né dispari
- Integrazione su intervalli simmetrici
- Decomposizione di una funzione in parte pari e parte dispari
- Dimostrazione dell'unicità della decomposizione
Funzioni Pari
Definizione. Una funzione \( f : X \to Y \) si dice pari se:
\[ \forall x \in X, \quad -x \in X \quad \text{e} \quad f(-x) = f(x) \]
In altre parole, la funzione è pari se il dominio è simmetrico rispetto all’origine e la funzione assume lo stesso valore in \( x \) e \( -x \).
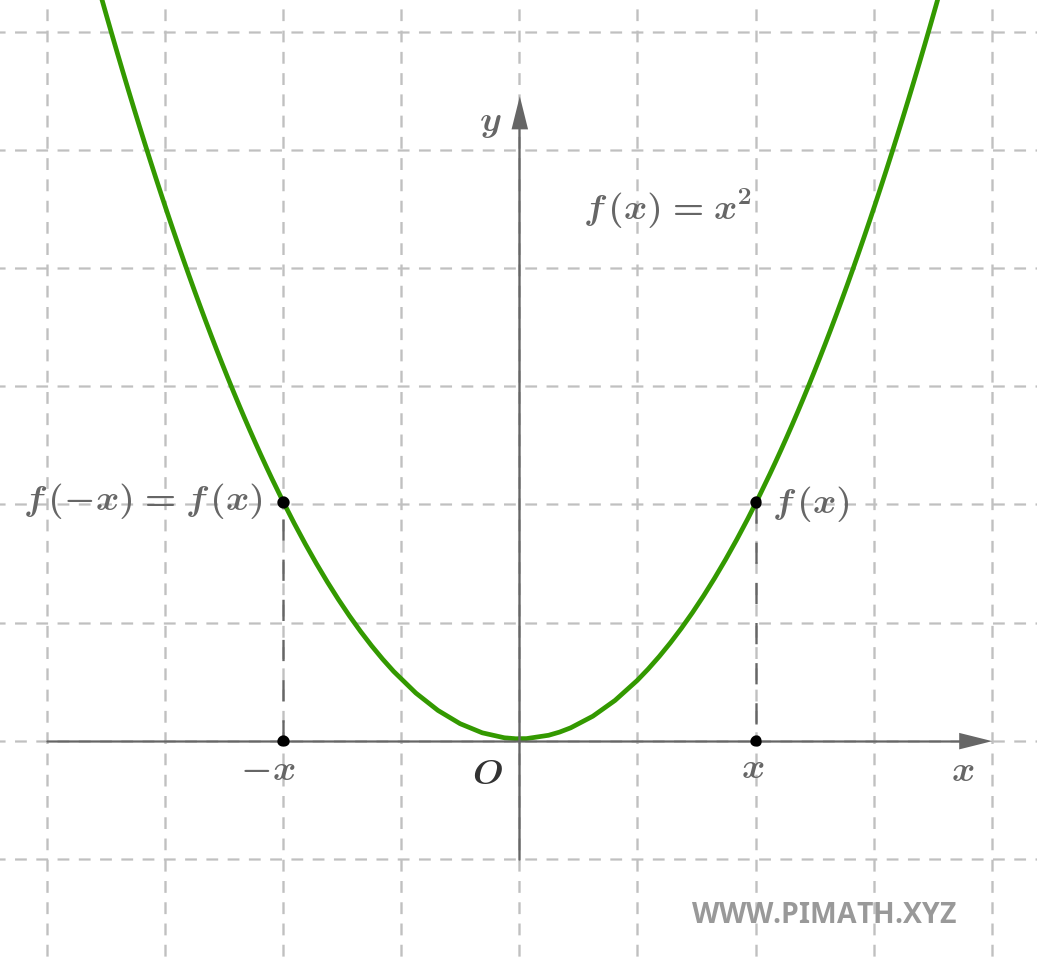
Esempio. La funzione \( f(x) = x^2 \) è pari, infatti per ogni \( x \in \mathbb{R} \), si ha \( (-x)^2 = x^2 \).
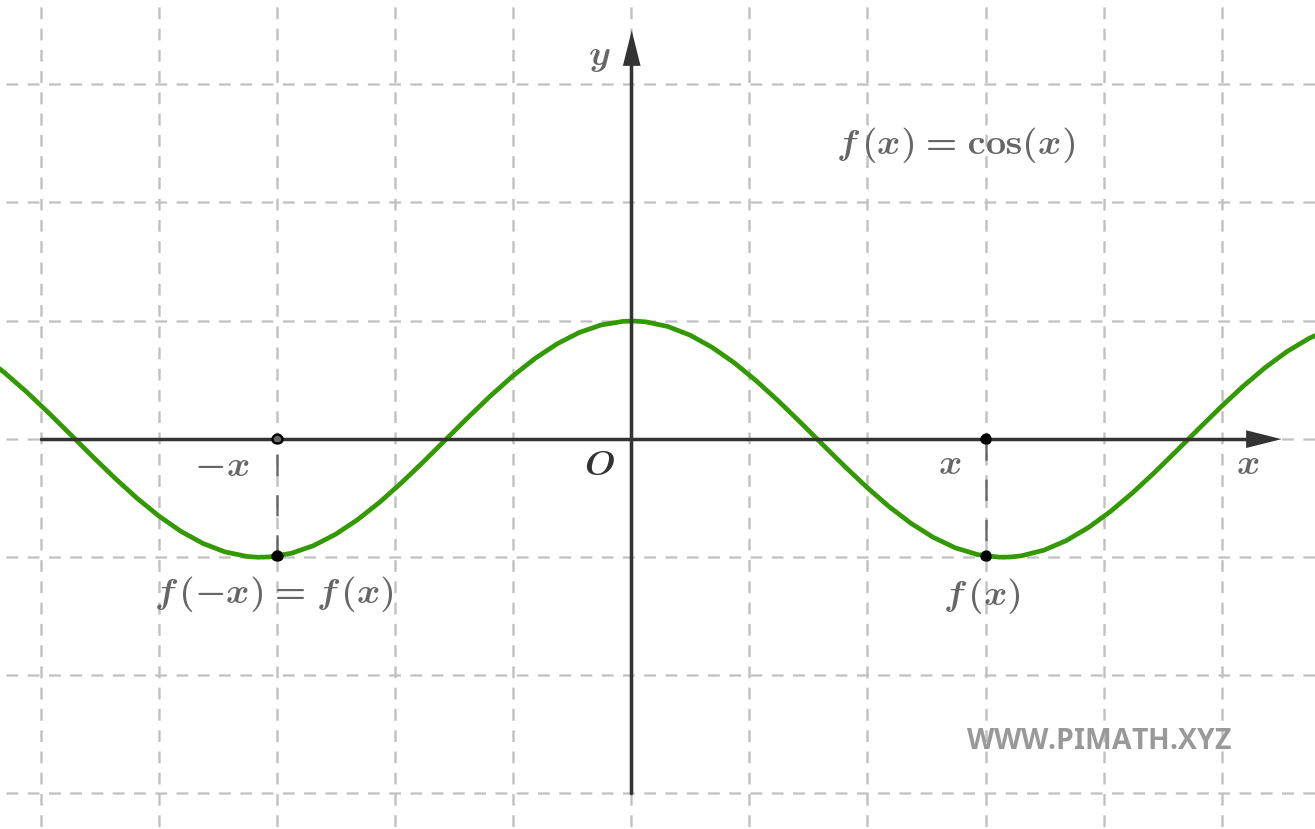
Esempio. La funzione \( f(x) = \cos(x) \) è pari, infatti per ogni \( x \in \mathbb{R} \), si ha \( \cos(-x) = \cos(x) \).
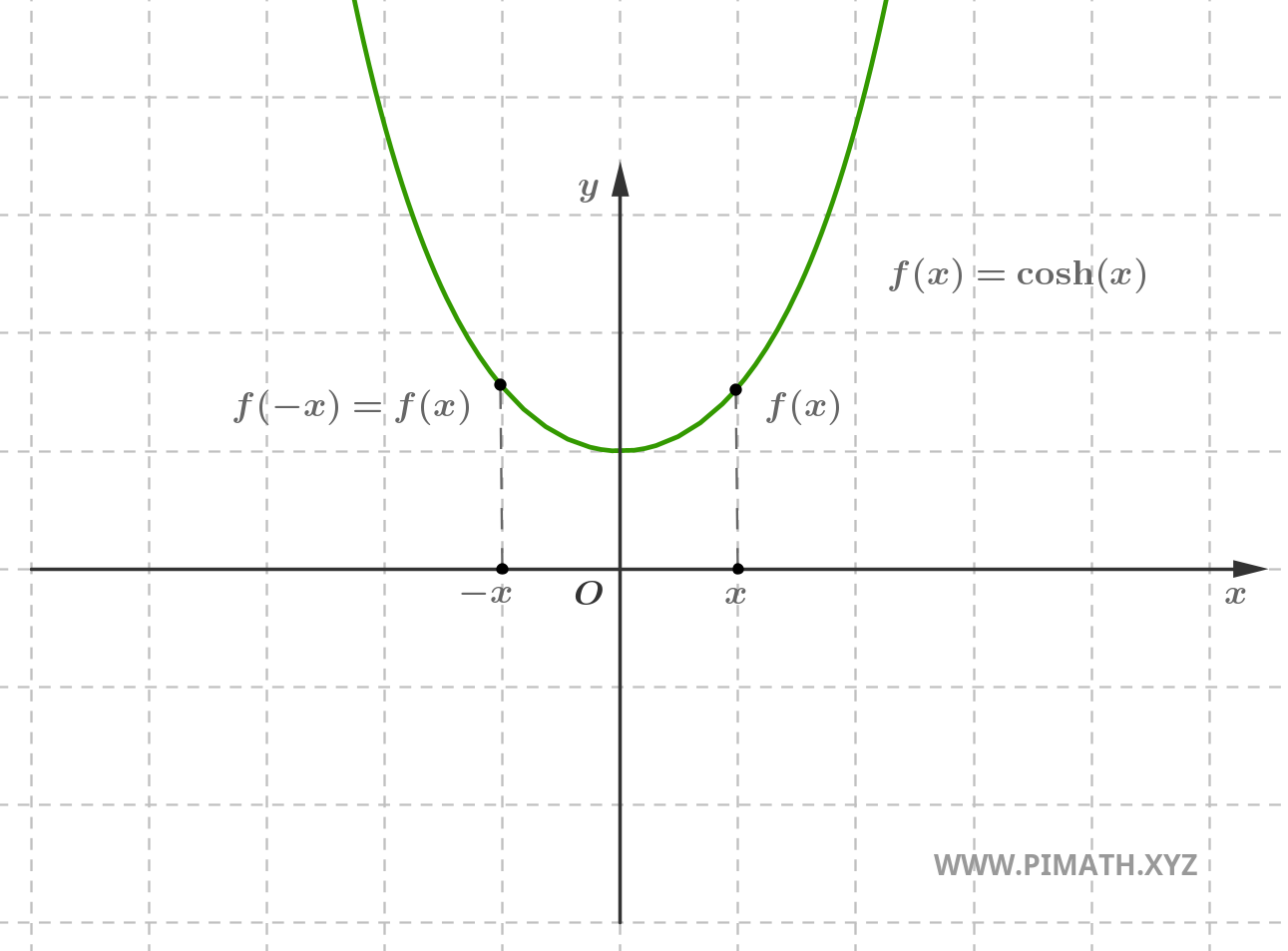
Esempio. La funzione \( f(x) = \cosh(x) \) è pari, infatti per ogni \( x \in \mathbb{R} \), si ha \( \cosh(-x) = \cosh(x) \).
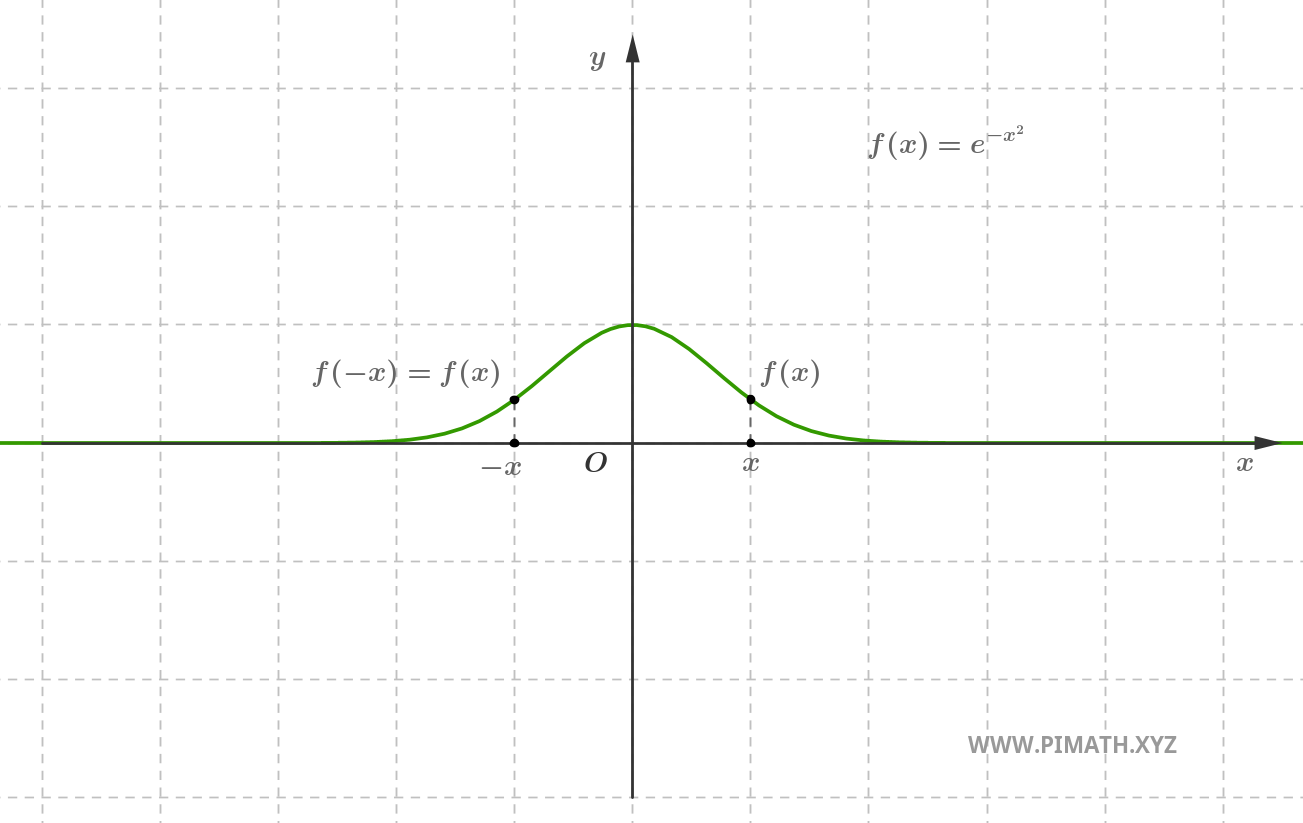
Esempio. La funzione \( f(x) = e^{-x^2} \) è pari, infatti per ogni \( x \in \mathbb{R} \), si ha \( e^{-(-x)^2} = e^{-x^2} \).
Somma di due funzioni pari
Siano \( f \) e \( g \) due funzioni pari, definite rispettivamente su \( D_f \) e \( D_g \). Consideriamo la funzione somma \( f + g \), definita sul dominio \( D = D_f \cap D_g \). Poiché \( D_f \) e \( D_g \) sono simmetrici, anche l’intersezione \( D \) è simmetrica. Per ogni \( x \in D \), abbiamo:
\[ (f + g)(-x) = f(-x) + g(-x) = f(x) + g(x) = (f + g)(x) \]
quindi \( f + g \) è una funzione pari.
Una funzione pari presenta simmetria rispetto all’asse delle ordinate. Pertanto, per analizzarne il grafico, è sufficiente studiarla per \( x \geq 0 \); il tratto per \( x < 0 \) si ottiene per simmetria.
Funzioni Dispari
Definizione. Una funzione \( f : X \to Y \) si dice dispari se:
\[ \forall x \in X, \quad -x \in X \quad \text{e} \quad f(-x) = -f(x) \]
In altre parole, la funzione è dispari se il dominio è simmetrico rispetto all’origine e la funzione assume valori opposti in \( x \) e \( -x \).
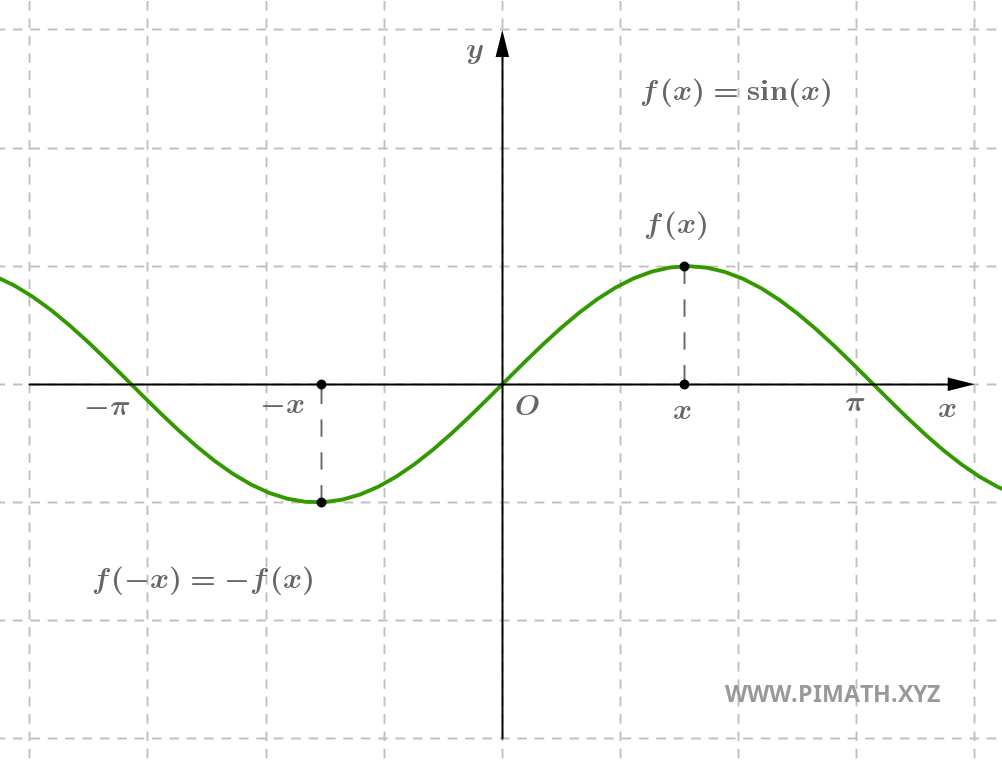
Esempio. La funzione \( f(x) = \sin(x) \) è dispari, infatti per ogni \( x \in \mathbb{R} \), si ha \( \sin(-x) = -\sin(x) \).
Esempio. La funzione \( f(x) = x^3 \) è dispari, infatti per ogni \( x \in \mathbb{R} \), si ha \( (-x)^3 = -x^3 \).
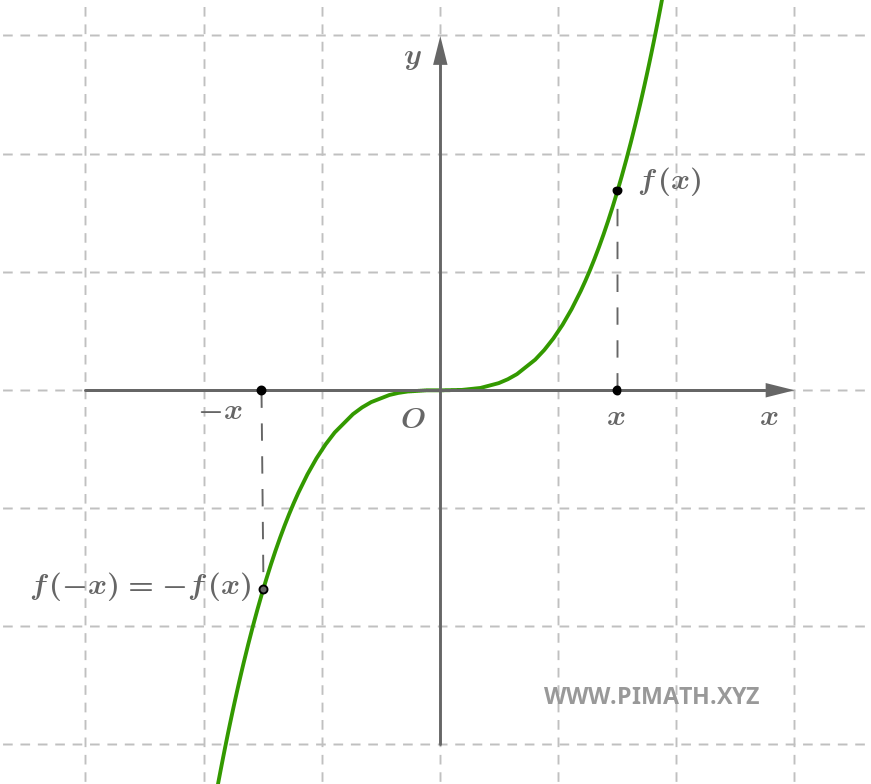
Una funzione dispari è simmetrica rispetto all’origine: ruotando il suo grafico di 180° attorno all’origine, si ottiene lo stesso grafico.
Somma di due funzioni dispari
Siano \( f \) e \( g \) due funzioni dispari, definite sui domini \( D_f \) e \( D_g \). Allora la somma \( f + g \), definita sul dominio comune \( D = D_f \cap D_g \), è anch’essa dispari.
Infatti, per ogni \( x \in D \), vale:
\[ (f + g)(-x) = f(-x) + g(-x) = -f(x) - g(x) = -(f(x) + g(x)) = -(f + g)(x) \]
Quindi \( f + g \) è una funzione dispari.
Funzioni né pari né dispari
Se una funzione non soddisfa né la relazione \( f(-x) = f(x) \), né \( f(-x) = -f(x) \), allora non è né pari né dispari.
Esempio. Le funzioni \( f(x) = e^x \) e \( f(x) = x + 1 \) non sono né pari né dispari.
Integrazione su intervalli simmetrici
Le funzioni pari e dispari sono particolarmente utili nel calcolo di integrali definiti su intervalli simmetrici rispetto all’origine.
Se \( f \) è pari, allora:
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
Se \( f \) è dispari, allora:
\[ \int_{-a}^{a} f(x) \, dx = 0 \]
Decomposizione di una funzione in parte pari e parte dispari
Sia \( f : X \to \mathbb{R} \) una funzione definita su un insieme simmetrico rispetto all’origine, cioè tale che \( x \in X \implies -x \in X \). In questo caso, la funzione \( f \) può essere scritta in modo unico come somma di una funzione pari e di una funzione dispari.
Precisamente, si definiscono:
\[ f_p(x) = \frac{f(x) + f(-x)}{2} \quad \text{(parte pari di \( f \))} \]
\[ f_d(x) = \frac{f(x) - f(-x)}{2} \quad \text{(parte dispari di \( f \))} \]
È immediato verificare che \( f_p(-x) = f_p(x) \) e \( f_d(-x) = -f_d(x) \), quindi \( f_p \) è pari e \( f_d \) è dispari. Inoltre, sommando le due espressioni si ottiene:
\[ f(x) = f_p(x) + f_d(x) \]
cioè ogni funzione \( f \) (definita su un insieme simmetrico) si può decomporre in modo unico nella somma di una funzione pari e una dispari.
Esempio. Consideriamo la funzione \( f(x) = e^x \), definita su tutto \( \mathbb{R} \). La parte pari è:
\[ f_p(x) = \frac{e^x + e^{-x}}{2} = \cosh x \]
mentre la parte dispari è:
\[ f_d(x) = \frac{e^x - e^{-x}}{2} = \sinh x \]
Si ha dunque la decomposizione:
\[ e^x = \cosh x + \sinh x \]
Osservazione: La decomposizione è possibile solo se il dominio della funzione è simmetrico rispetto all’origine. Inoltre, la scrittura \( f = f_p + f_d \) è unica: esiste una sola funzione pari e una sola funzione dispari la cui somma restituisce \( f \).
Dimostrazione dell'unicità della decomposizione
Supponiamo che una funzione \( f : X \to \mathbb{R} \), definita su un insieme simmetrico rispetto all’origine, si possa scrivere in due modi distinti come somma di una funzione pari e di una funzione dispari:
\[ f(x) = f_p(x) + f_d(x) = g_p(x) + g_d(x), \]
dove \( f_p \), \( g_p \) sono pari e \( f_d \), \( g_d \) sono dispari.
Allora:
\[ f_p(x) - g_p(x) = g_d(x) - f_d(x) \]
Chiamiamo \( h(x) = f_p(x) - g_p(x) = g_d(x) - f_d(x) \). La funzione \( h \) è quindi pari (come differenza di due funzioni pari) e dispari (come differenza di due funzioni dispari).
Ma se una funzione è contemporaneamente pari e dispari, allora:
\[ h(x) = h(-x) \quad \text{e} \quad h(x) = -h(-x) \implies h(x) = -h(x) \]
cioè \( h(x) = 0 \) per ogni \( x \in X \).
Dunque \( f_p(x) = g_p(x) \) e \( f_d(x) = g_d(x) \), il che dimostra l’unicità della decomposizione.

