La retta è un concetto primitivo della geometria euclidea, ossia non definibile in termini più elementari, ma assunto come ente fondamentale. Essa viene intuitivamente descritta come l’insieme infinito di punti disposti secondo una direzione costante, estendendosi indefinitamente in entrambe le direzioni. In un sistema di riferimento cartesiano, una retta è rappresentabile mediante un’equazione lineare e caratterizzata da un coefficiente angolare che ne determina l’inclinazione rispetto all’asse delle ascisse.
Indice
- Come Trovare L'equazione della Retta Passante per due Punti
- Come Trovare L'equazione Esplicita della Retta
- Come Trovare L'equazione Implicita della Retta
- Significato Geometrico del Coefficiente Angolare
- Come Trovare l'equazione Parametrica della Retta
- Come Trovare la Retta Perpendicolare ad una Data Retta
- Esercizi Svolti sulla Retta
Come Trovare L'equazione della Retta Passante per due Punti
Supponiamo di conoscere due punti distinti del piano cartesiano: \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \).
L’equazione dei punti appartenenti alla retta passante per \( P_1 \) e \( P_2 \) è data dalla seguente formula:
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1}. \]
Infatti, basta osservare che i triangoli \( \triangle P_1P'P \) e \( \triangle P_1P'_2P_2 \) in figura:
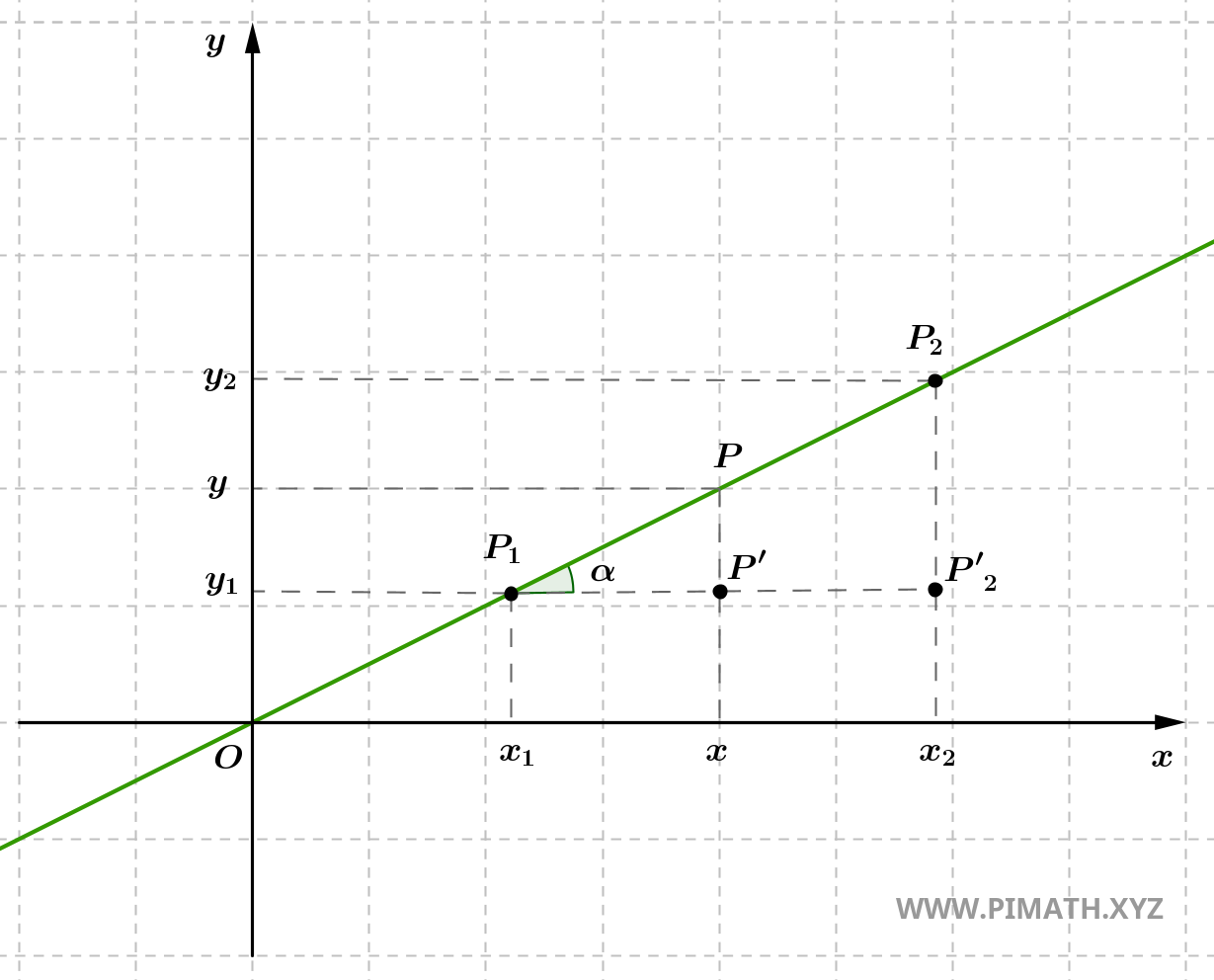
sono simili in base al primo criterio di similitudine, il quale afferma che due triangoli sono simili se hanno due angoli rispettivamente congruenti. In questo caso, entrambi i triangoli presentano un angolo retto e un angolo acuto congruente, determinato dall’inclinazione della retta rispetto all’asse \( x \). Ne consegue la proporzionalità tra i lati corrispondenti.
\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]
Risolvendo rispetto a \( y \), si ottiene la forma esplicita dell’equazione della retta:
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \]
L’angolo acuto comune ai due triangoli, indicato spesso con \( \alpha \), rappresenta l’angolo d’inclinazione della retta rispetto all’asse \( x \). Questo angolo ha un ruolo fondamentale nella geometria della retta, poiché la sua tangente fornisce la pendenza della retta, ovvero: \[ m = \tan \alpha = \frac{y_2 - y_1}{x_2 - x_1}. \] Questo legame consente di interpretare la pendenza come una misura dell’inclinazione angolare della retta nel piano cartesiano.
Come Trovare L'equazione Esplicita della Retta
L'equazione della retta passante per due punti distinti \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) può essere scritta in forma esplicita utilizzando la cosiddetta forma punto-pendenza:
\[ y = y_1 + m(x - x_1) \]
dove
\[ m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]
è il coefficiente angolare della retta. Questa espressione permette di calcolare il valore di \( y \) corrispondente a ogni valore assegnato di \( x \), partendo da un punto noto sulla retta e dalla sua pendenza.
A partire da questa forma, è possibile ricavare la forma esplicita canonica dell'equazione della retta, che è:
\[ y = mx + q \]
In questa equazione:
- \( m \) è il coefficiente angolare, che rappresenta la pendenza della retta;
- \( q \) è l'ordinata all'origine, ovvero il valore di \( y \) nel punto in cui la retta interseca l'asse delle ordinate (cioè quando \( x = 0 \)).
Questa forma è particolarmente utile perché rende immediatamente evidenti sia la direzione della retta (tramite \( m \)) sia il suo punto di intersezione con l'asse \( y \) (tramite \( q \)). Se si conoscono \( m \) e \( q \), è possibile tracciare la retta senza bisogno di altri punti.
Per passare dalla forma punto-pendenza a quella canonica, basta sviluppare i calcoli e isolare \( y \). Ad esempio:
\[ y = y_1 + m(x - x_1) = mx + (y_1 - mx_1) \]
Da cui si ottiene direttamente:
\[ y = mx + q \quad \text{con} \quad q = y_1 - mx_1 \]
Come Trovare L'equazione Implicita della Retta
Partiamo dalla forma punto-pendenza dell'equazione della retta, che passa per due punti \( (x_1, y_1) \) e \( (x_2, y_2) \):
\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]
Moltiplichiamo entrambi i membri per \( x_2 - x_1 \neq 0 \):
\[ (x_2 - x_1)(y - y_1) = (y_2 - y_1)(x - x_1) \]
Sviluppiamo entrambi i membri:
\[ (x_2 - x_1)y - (x_2 - x_1)y_1 = (y_2 - y_1)x - (y_2 - y_1)x_1 \]
Portiamo tutti i termini al primo membro:
\[ (x_2 - x_1)y - (y_2 - y_1)x + \left( (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \right) = 0 \]
Questa è la forma implicita dell'equazione della retta. Se definiamo i coefficienti come:
\[ \begin{cases} a = -(y_2 - y_1) \\ b = x_2 - x_1 \\ c = (y_2 - y_1)x_1 - (x_2 - x_1)y_1 \end{cases} \]
l'equazione assume la forma generale:
\[ ax + by + c = 0 \]
Alternativamente, se introduciamo la pendenza \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \), possiamo partire dalla forma esplicita della retta:
\[ y = m(x - x_1) + y_1 \]
Riportiamo tutto al primo membro per ottenere la forma implicita:
\[ y - m x + (m x_1 - y_1) = 0 \]
Quindi la forma implicita con pendenza \( m \) è:
\[ a = -m, \quad b = 1, \quad c = m x_1 - y_1 \]
e la forma generale:
\[ ax + by + c = 0 \]
La forma implicita è utile quando si vogliono studiare proprietà geometriche della retta o verificare l'appartenenza di un punto senza dover risolvere per \( y \).
Significato Geometrico del Coefficiente Angolare
Nel contesto di questa equazione, il termine:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
rappresenta la pendenza della retta, ovvero il coefficiente angolare. La pendenza è una misura dell'inclinazione della retta rispetto all'asse delle ascisse (l'asse \( x \)). Se la pendenza è positiva, la retta è crescente (sale da sinistra a destra); se è negativa, la retta è decrescente (scende da sinistra a destra).
In altre parole, la pendenza descrive la velocità con cui la retta cresce o decresce in relazione all'asse delle ascisse \( x \). La pendenza è un parametro cruciale per determinare l'orientamento della retta nel piano cartesiano. A seconda del valore della pendenza, possiamo fare le seguenti osservazioni:
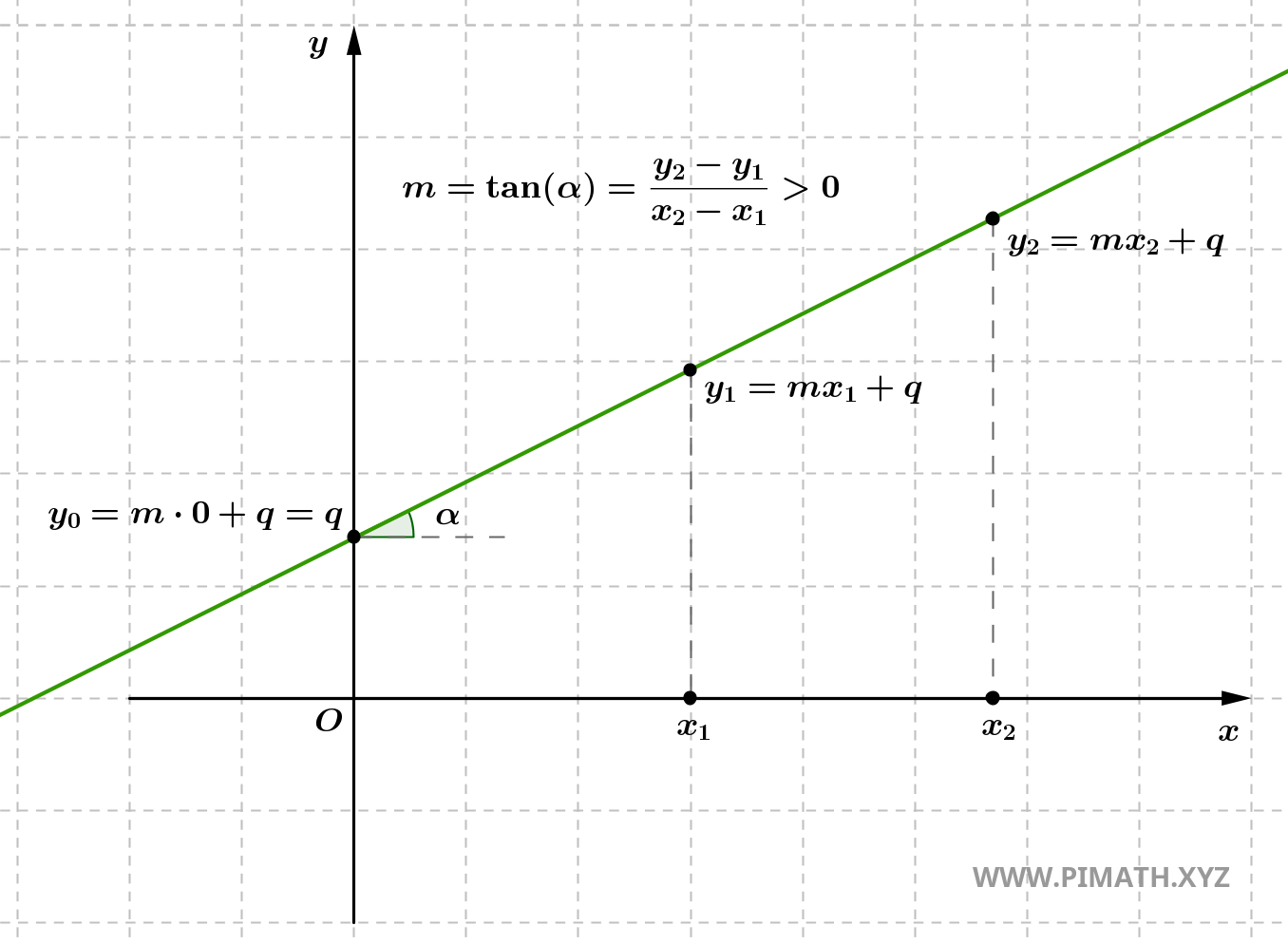
- Se \( m > 0 \), la retta è crescente, ovvero sale da sinistra a destra. Questo significa che per ogni incremento in \( x \), anche \( y \) aumenta. La retta forma un angolo acuto con l'asse \( x \).
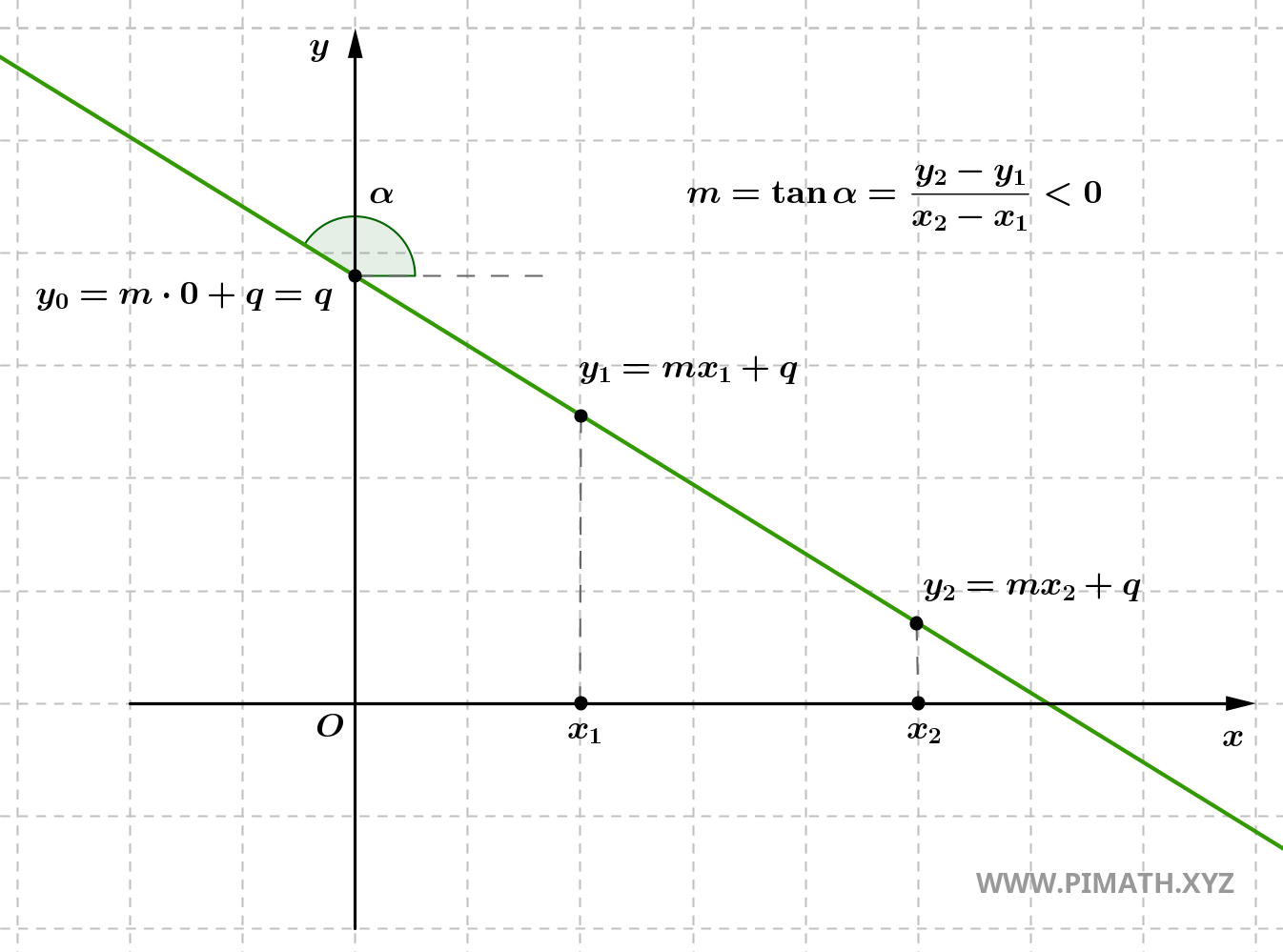
- Se \( m < 0 \), la retta è decrescente, ovvero scende da sinistra a destra. In questo caso, per ogni incremento in \( x \), il valore di \( y \) diminuisce. La retta forma un angolo ottuso con l'asse \( x \).
- Se \( y_2 = y_1 \), la pendenza è nulla, il che implica che la retta è orizzontale. In questo caso, non esiste un cambiamento verticale (la differenza tra le ordinate \( y_2 - y_1 \) è zero). La retta è parallela all'asse \( x \) e non ha alcuna inclinazione verticale.
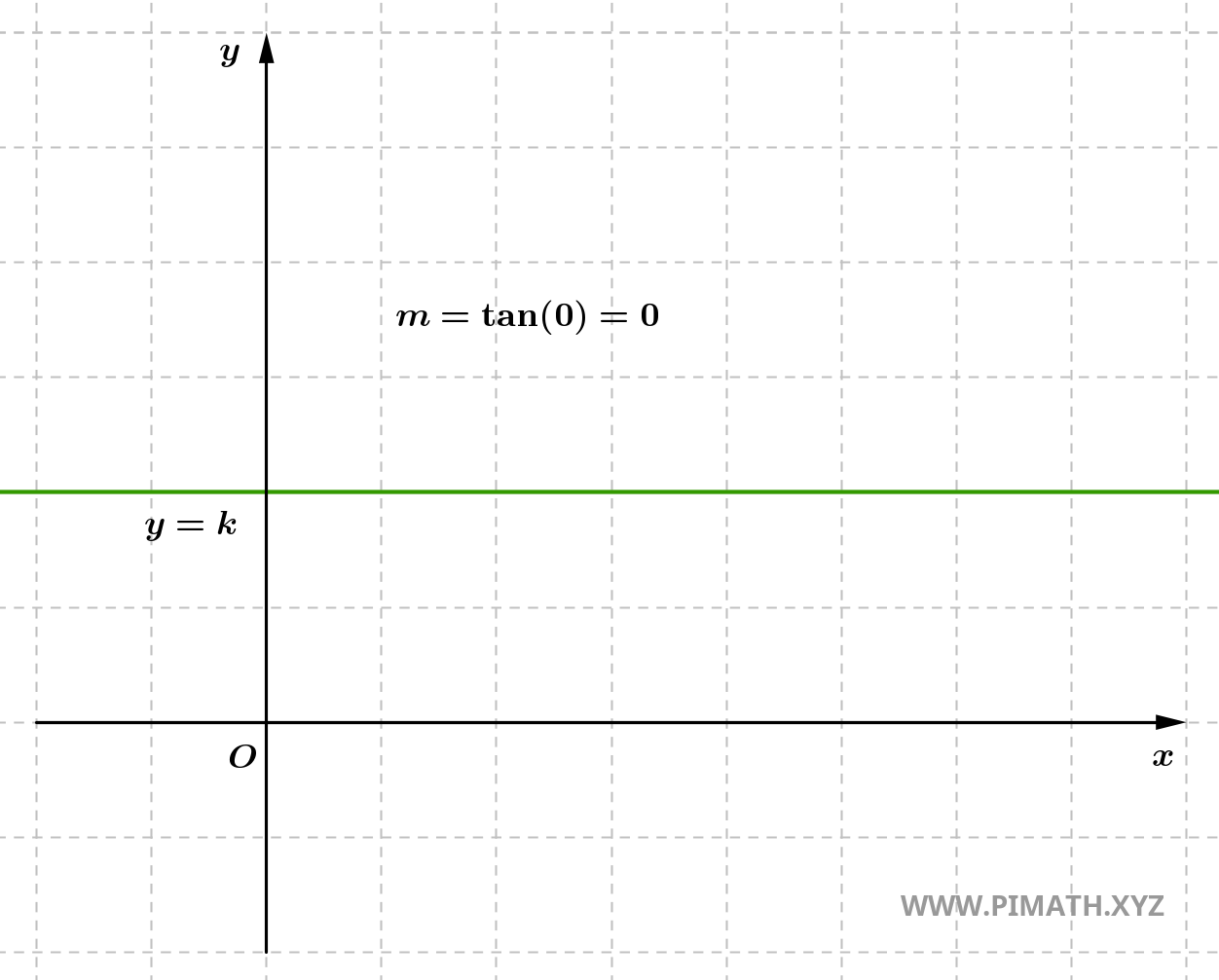
- Se \( x_2 = x_1 \), la pendenza è indefinita, il che implica che la retta è verticale. In questo caso, non esiste un cambiamento orizzontale (la differenza tra le ascisse \( x_2 - x_1 \) è zero), quindi non si può definire una pendenza numerica. La retta è parallela all'asse \( y \) e non ha alcuna inclinazione orizzontale.
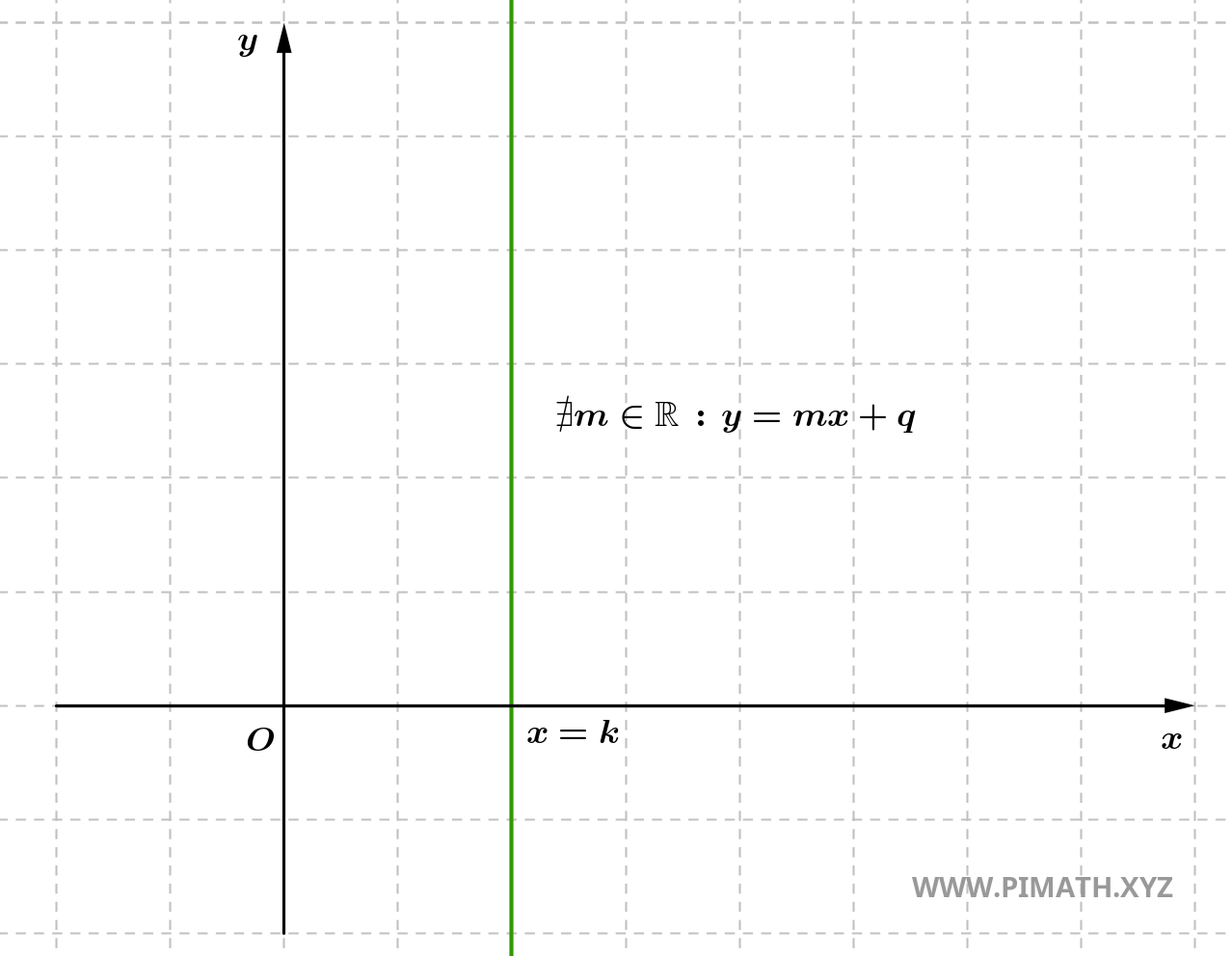
In generale, la pendenza \( m \) ci offre informazioni importanti sul comportamento della retta. Se la retta è crescente, il valore di \( y \) aumenta all'aumentare di \( x \); se è decrescente, il valore di \( y \) diminuisce all'aumentare di \( x \); se la retta è verticale, significa che \( y \) non dipende da \( x \) e la retta non ha alcuna inclinazione orizzontale.
Come Trovare l'equazione Parametrica della Retta
La retta passante per i punti \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) può essere descritta anche in forma parametrica. In questa rappresentazione, le coordinate \( x \) e \( y \) di un punto sulla retta vengono espresse in funzione di un parametro reale \( t \), che varia lungo la retta.
L'equazione parametrica della retta è data da:
\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]
Qui, \( t \) è il parametro che può assumere qualsiasi valore reale. Quando \( t \) varia, il punto \( (x, y) \) si sposterà lungo la retta che collega i due punti \( P_1 \) e \( P_2 \).
La forma parametrica rappresenta quindi una famiglia di punti sulla retta, in cui il parametro \( t \) definisce univocamente ogni punto della retta. Quando \( t = 0 \), si ottiene il punto \( P_1(x_1, y_1) \); quando \( t = 1 \), si ottiene il punto \( P_2(x_2, y_2) \). I valori di \( t \) tra 0 e 1 descrivono i punti della retta tra \( P_1 \) e \( P_2 \), mentre i valori di \( t \) superiori a 1 o inferiori a 0 estendono la retta oltre questi punti.
La formula parametrica si basa sul concetto di vettore direttore, che è il vettore che collega \( P_1 \) e \( P_2 \). Infatti, la differenza \( (x_2 - x_1, y_2 - y_1) \) è il vettore direttore della retta, e il parametro \( t \) è il fattore di scala che consente di spostarsi lungo la retta.
La forma parametrica è particolarmente utile in vari ambiti della geometria analitica, come nello studio delle curve in generale.
Come Trovare la Retta Perpendicolare ad una Data Retta
Quando due rette sono perpendicolari, la loro pendenza è legata da una relazione ben precisa. Se una retta ha pendenza \( m \), la pendenza della retta perpendicolare ad essa è data da:
\[ m_\perp = -\frac{1}{m}. \]
Questa formula esprime il fatto che il prodotto delle pendenze di due rette perpendicolari è uguale a \(-1\). La ragione di questa relazione può essere vista nel fatto che gli angoli formati dalle due rette devono essere di 90° (un angolo retto), e quindi la tangente dell'angolo tra le rette deve soddisfare questa condizione.
Per trovare l'equazione della retta perpendicolare che passa per un punto \( (x_1, y_1) \), possiamo usare la forma punto-pendenza. La pendenza della retta perpendicolare è \( -\displaystyle \frac{1}{m} \), quindi l'equazione della retta perpendicolare sarà:
\[ y - y_1 = -\frac{1}{m} (x - x_1). \]
In questa equazione, \( (x_1, y_1) \) è il punto attraverso il quale passa la retta perpendicolare, mentre \( m \) è la pendenza della retta originale. La formula descrive una retta che ha la pendenza opposta e inversa rispetto alla retta originale.
Se la retta originale è rappresentata dall'equazione \( y = mx + q \), la retta perpendicolare avrà la pendenza \( m_\perp = -\displaystyle \frac{1}{m} \) e sarà scritta nella forma \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), dove \( (x_1, y_1) \) è il punto di intersezione tra la retta originale e la retta perpendicolare.
Questa proprietà delle rette perpendicolari è fondamentale in molti ambiti della geometria, della trigonometria e della fisica, in particolare quando si studiano angoli e traiettorie perpendicolari tra loro.
Esercizi Svolti sulla Retta
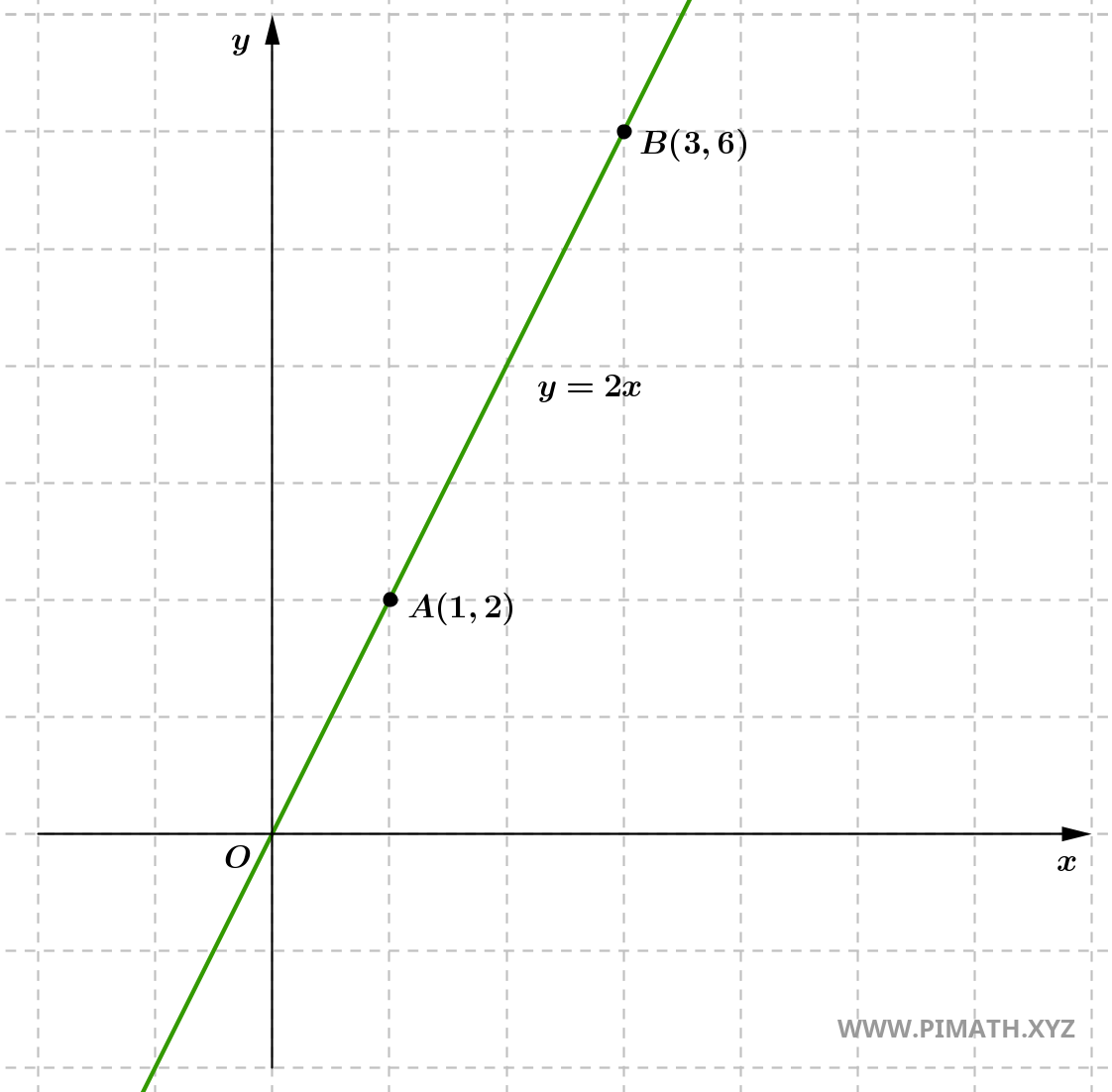
Esercizio 1: Determina l'equazione esplicita della retta passante per \( A(1, 2) \) e \( B(3, 6) \).
Soluzione. Calcoliamo il coefficiente angolare della retta:
\[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2. \]
- Utilizziamo l'equazione punto-pendenza per determinare l'equazione della retta che passa per \( A(1, 2) \) e coefficiente angolare \( m = 2 \): \[ y - 2 = 2(x - 1). \]
- Sviluppando l'equazione: \[ y - 2 = 2x - 2. \]
- Semplificando: \[ y = 2x - 2 + 2 = 2x. \]
Quindi, l'equazione della retta passante per i punti \( A(1, 2) \) e \( B(3, 6) \) è \[ y = 2x. \]
Verifica: Possiamo verificare che entrambi i punti soddisfano questa equazione:
- Per \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
- Per \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]
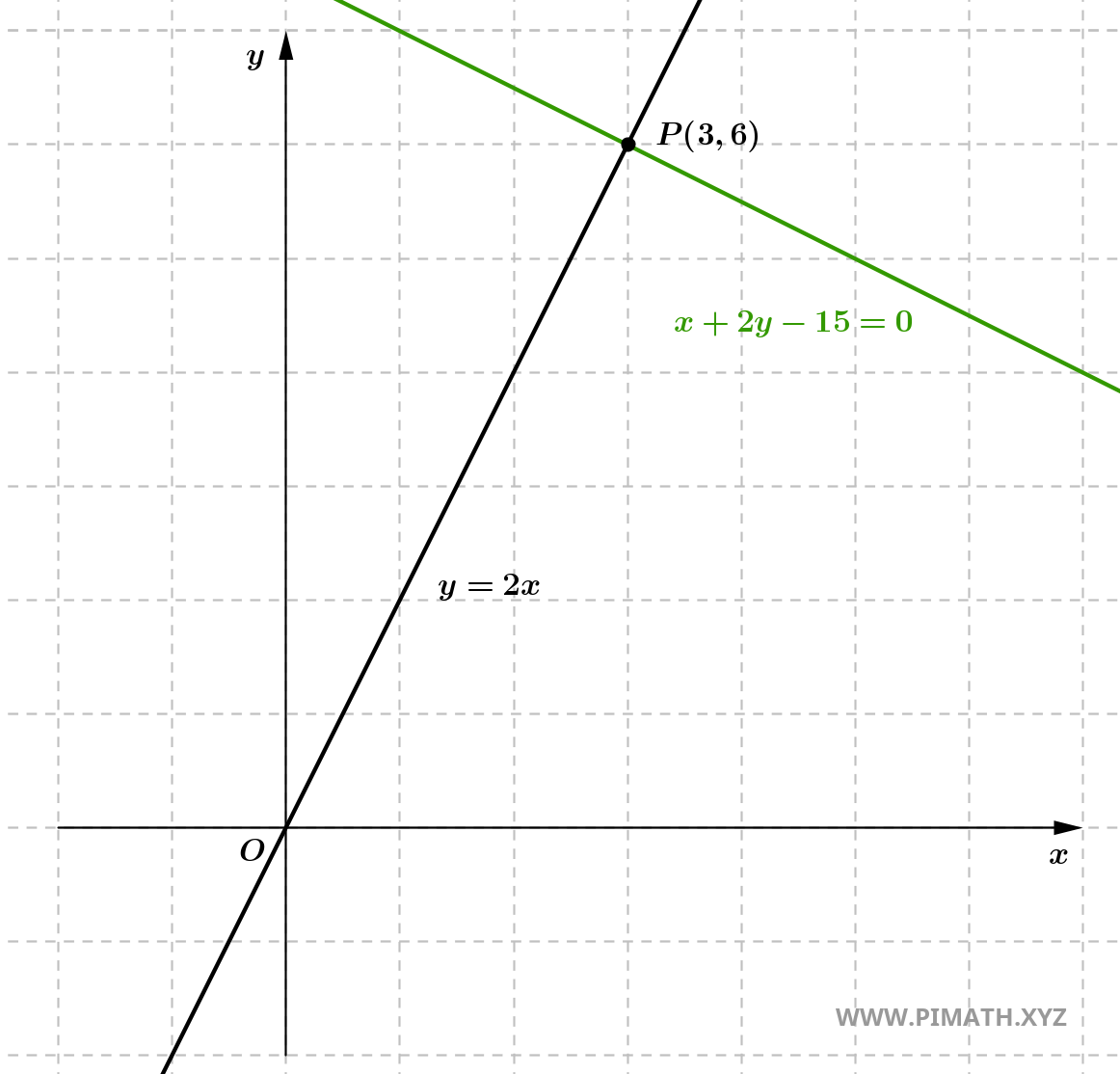
Esercizio 2: Determina l'equazione della retta perpendicolare alla retta \( y = 2x \) e passante per il punto \( P(3, 6) \).
Soluzione. La retta data ha coefficiente angolare \( m = 2 \). Il coefficiente angolare della retta perpendicolare sarà:
\[ m_{\perp} = -\frac{1}{2}. \]
- Utilizziamo l'equazione punto-pendenza per determinare l'equazione della retta che passa per \( P(3, 6) \) e ha coefficiente angolare \( m_{\perp} = -\frac{1}{2} \): \[ y - 6 = -\frac{1}{2}(x - 3). \]
- Sviluppiamo l'equazione: \[ y - 6 = -\frac{1}{2}x + \frac{3}{2}. \]
- Portiamo il termine noto a destra: \[ y = -\frac{1}{2}x + \frac{3}{2} + 6 = -\frac{1}{2}x + \frac{15}{2}. \]
Quindi, l'equazione della retta cercata è: \[ y = -\frac{1}{2}x + \frac{15}{2}. \]
Forma implicita: Moltiplichiamo entrambi i membri per 2:
\[ 2y = -x + 15 \quad \Rightarrow \quad x + 2y - 15 = 0. \]
Verifica: Sostituendo le coordinate di \( P(3, 6) \) nell'equazione esplicita:
- \[ y = -\frac{1}{2}x + \frac{15}{2} \quad \Rightarrow \quad 6 = -\frac{1}{2} \cdot 3 + \frac{15}{2} = -\frac{3}{2} + \frac{15}{2} = \frac{12}{2} = 6. \]
Il punto appartiene alla retta, quindi la soluzione è corretta.
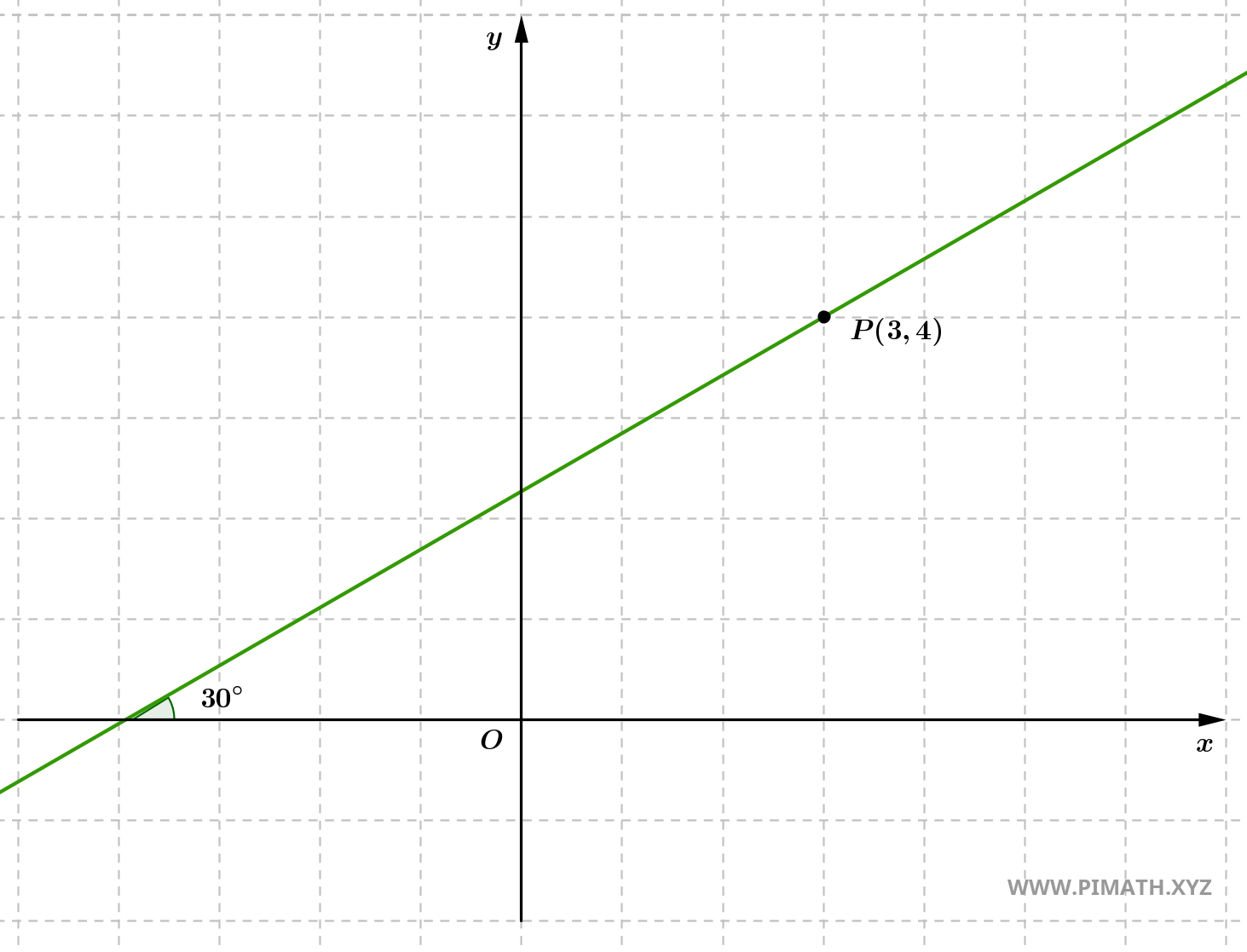
Esercizio 3: Determina l'equazione della retta passante per il punto \( P(3, 4) \) e che formi un angolo di \( 30^\circ \) con l'asse delle ascisse.
Soluzione. L’angolo che una retta forma con l’asse delle ascisse è legato al coefficiente angolare tramite la tangente:
\[ m = \tan(30^\circ) = \tan\left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{3}}. \]
- Utilizziamo l’equazione punto-pendenza con il punto \( P(3, 4) \) e coefficiente angolare \( m = \frac{1}{\sqrt{3}} \): \[ y - 4 = \frac{1}{\sqrt{3}}(x - 3). \]
- Sviluppando l’equazione: \[ y - 4 = \frac{1}{\sqrt{3}}x - \frac{3}{\sqrt{3}} = \frac{1}{\sqrt{3}}x - \sqrt{3}. \]
- Aggiungiamo 4 a entrambi i membri: \[ y = \frac{1}{\sqrt{3}}x - \sqrt{3} + 4. \]
- Semplificando il termine noto: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Quindi, l’equazione della retta cercata è: \[ y = \frac{1}{\sqrt{3}}x + (4 - \sqrt{3}). \]
Verifica: Sostituendo \( x = 3 \), otteniamo: \[ y = \frac{1}{\sqrt{3}} \cdot 3 + (4 - \sqrt{3}) = \sqrt{3} + 4 - \sqrt{3} = 4. \]
- Il punto \( P(3, 4) \) appartiene alla retta, quindi la soluzione è corretta.
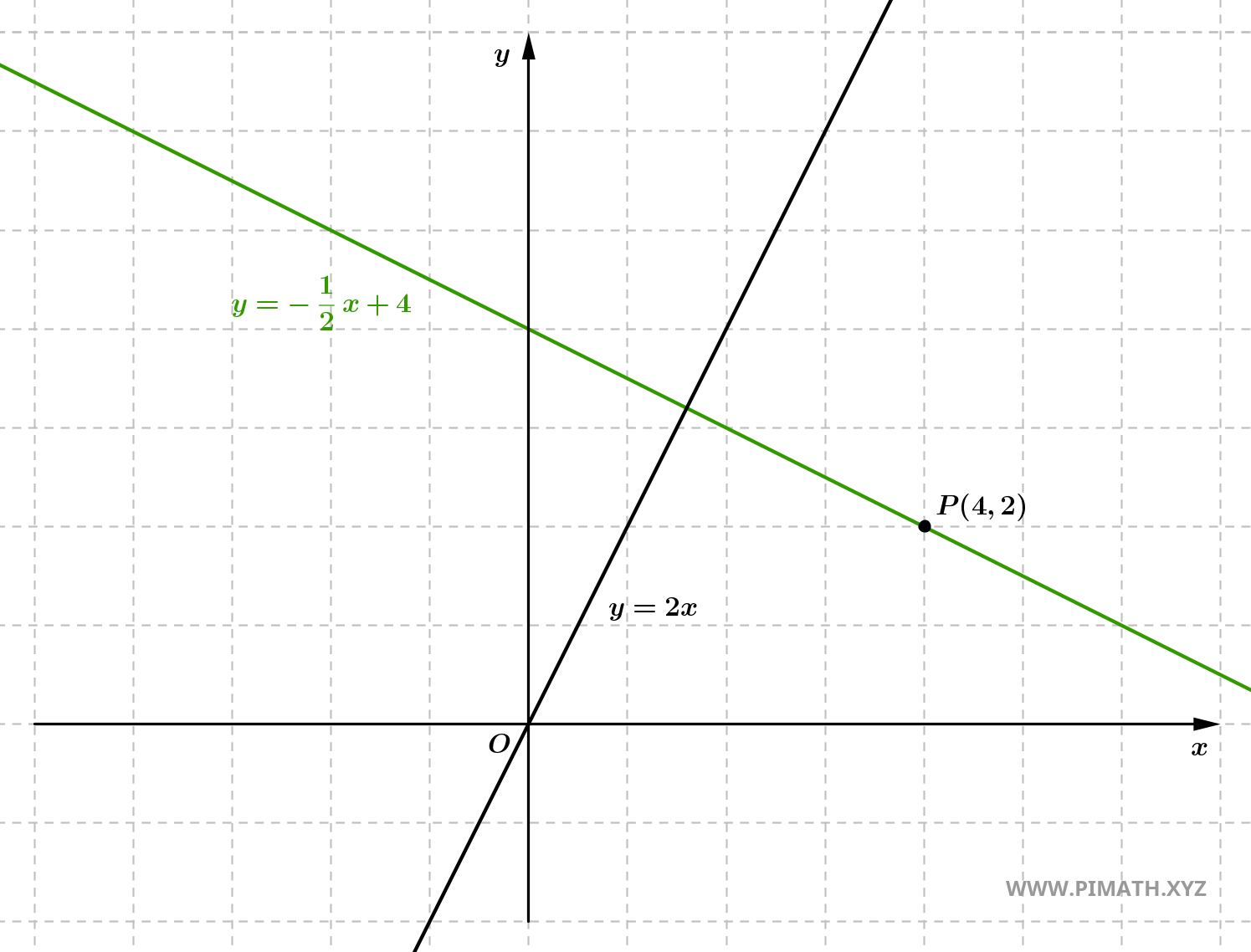
Esercizio 4: Determina l'equazione della retta perpendicolare alla retta \( y = 2x \) e passante per il punto \( P(4, 2) \).
Soluzione. La retta data ha coefficiente angolare \( m = 2 \). Il coefficiente angolare della retta perpendicolare sarà:
\[ m_{\perp} = -\frac{1}{2}. \]
- Utilizziamo l'equazione punto-pendenza per determinare l'equazione della retta che passa per \( P(4, 2) \) e ha coefficiente angolare \( m_{\perp} = -\frac{1}{2} \): \[ y - 2 = -\frac{1}{2}(x - 4). \]
- Sviluppiamo l'equazione: \[ y - 2 = -\frac{1}{2}x + 2. \]
- Portiamo il termine noto a destra: \[ y = -\frac{1}{2}x + 2 + 2 = -\frac{1}{2}x + 4. \]
Quindi, l'equazione della retta cercata è: \[ y = -\frac{1}{2}x + 4. \]
Forma implicita: Moltiplichiamo entrambi i membri per 2:
\[ 2y = -x + 8 \quad \Rightarrow \quad x + 2y - 8 = 0. \]
Verifica: Sostituendo le coordinate di \( P(4, 2) \) nell'equazione esplicita:
- \[ y = -\frac{1}{2}x + 4 \quad \Rightarrow \quad 2 = -\frac{1}{2} \cdot 4 + 4 = -2 + 4 = 2. \]
Il punto appartiene alla retta, quindi la soluzione è corretta.
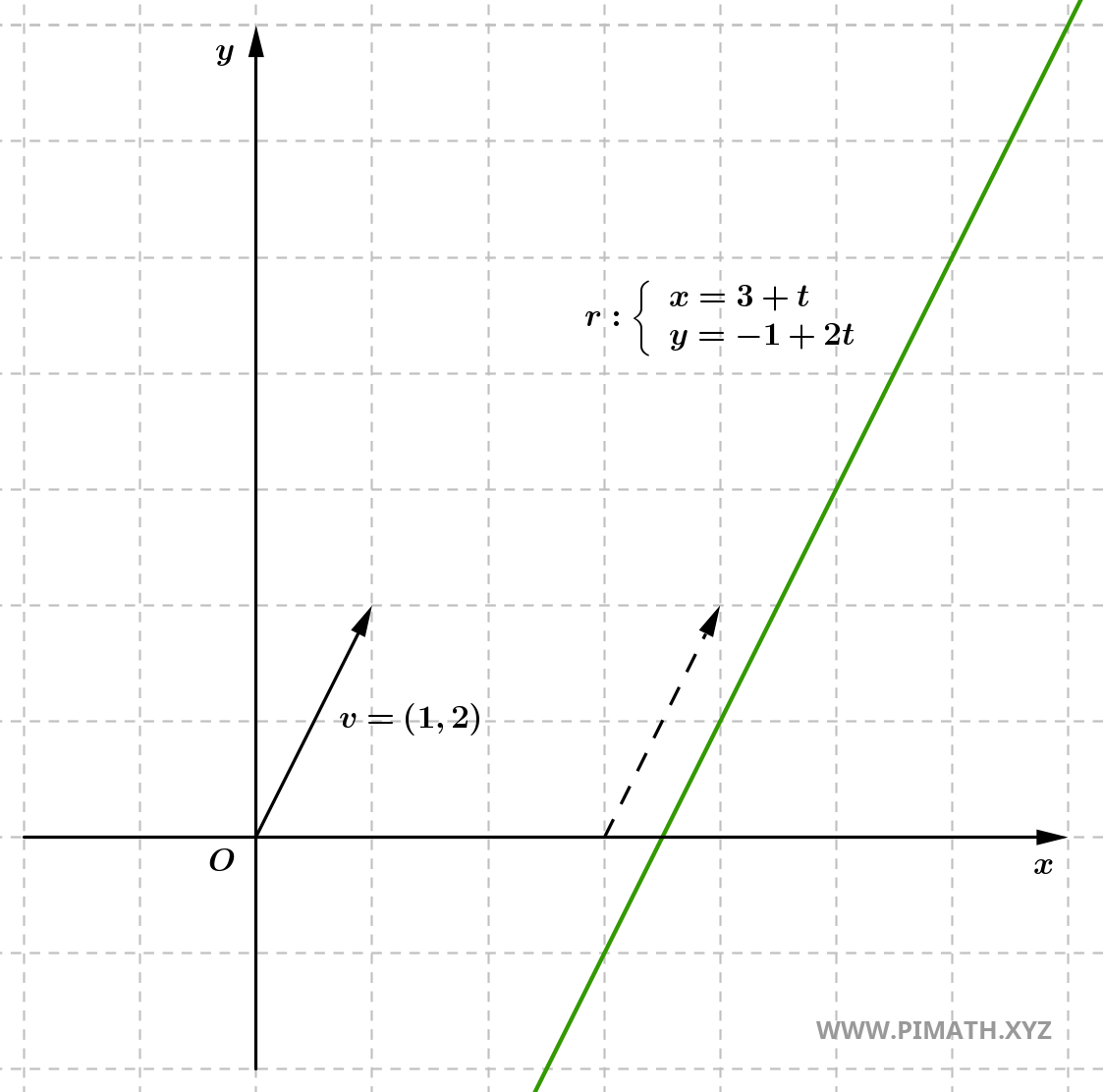
Esercizio 5: Scrivi l'equazione parametrica della retta passante per \( A(3, -1) \) e \( B(4, 1) \). Successivamente, scrivi l'equazione parametrica in forma cartesiana.
Soluzione. Calcoliamo il vettore direttore \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), che rappresenta la direzione della retta:
\[ \boldsymbol{v} = (4 - 3,\ 1 - (-1)) = (1,\ 2). \]
Le equazioni parametriche della retta sono:
\[ r: \begin{cases} x = 3 + t \\ y = -1 + 2t \end{cases} \quad \text{con} \quad t \in \mathbb{R}. \]
Passiamo ora alla forma cartesiana. Ricaviamo \( t \) dalla prima equazione:
\[ x = 3 + t \quad \Rightarrow \quad t = x - 3. \]
Sostituendo nella seconda:
\[ y = -1 + 2(x - 3) = -1 + 2x - 6 = 2x - 7. \]
Dunque la forma esplicita è:
\[ y = 2x - 7. \]
Infine, portando tutto al primo membro otteniamo la forma implicita:
\[ 2x - y - 7 = 0. \]