La parabola è il luogo geometrico dei punti del piano per i quali la distanza da un punto fisso (fuoco) è uguale alla distanza da una retta fissa (direttrice). Ha un asse di simmetria che passa per il fuoco ed è perpendicolare alla direttrice. È una curva aperta e simmetrica rispetto al proprio asse, con numerose applicazioni in fisica e geometria.
Indice
- Equazione Canonica della Parabola
- Equazione Canonica di una Parabola con Asse Verticale o Orizzontale
- Parabola Traslata nel Piano
- Vertice, Fuoco, Direttrice e Assi di Simmetria
- Equazione della Parabola Noti il Vertice e un Punto
- Esercizi Svolti sulla Parabola
Equazione Canonica della Parabola
Una parabola è il luogo geometrico dei punti \( P(x, y) \) del piano che hanno la stessa distanza da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice.
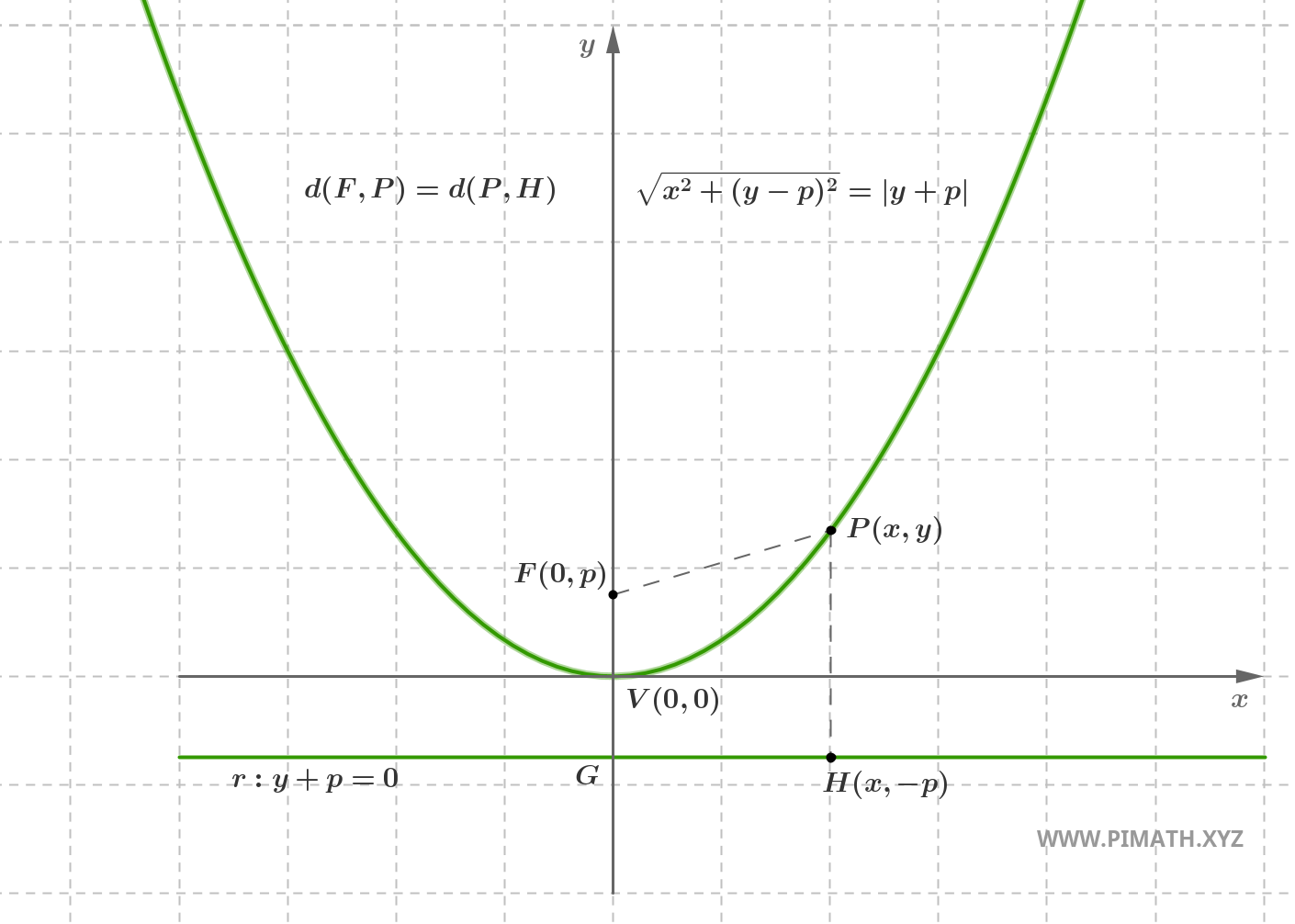
Sia \( F(0, p) \) con \( p > 0 \) il fuoco e sia \( r \) la direttrice, di equazione \( y = -p \). Per definizione, i punti \( P(x, y) \) della parabola soddisfano:
\[ \text{d}(P, F) = \text{d}(P, r) \]
Calcoliamo la distanza tra \( P(x, y) \) e il fuoco \( F(0, p) \):
\[ \text{d}(P, F) = \sqrt{(x - 0)^2 + (y - p)^2} = \sqrt{x^2 + (y - p)^2} \]
Ora, calcoliamo la distanza tra \( P(x, y) \) e la retta direttrice \( y = -p \):
\[ \text{d}(P, r) = |y - (-p)| = |y + p| \]
Infine, imponiamo l'uguaglianza tra le due distanze:
\[ \sqrt{x^2 + (y - p)^2} = |y + p| \]
Osservazione: poiché la parabola si trova sopra la direttrice (dato che il fuoco è sopra la direttrice per \( p > 0 \)), tutti i punti della parabola soddisfano \( y \geq -p \). Quindi \( y + p \geq 0 \) e possiamo togliere il valore assoluto:
\[ \sqrt{x^2 + (y - p)^2} = y + p \]
Eleviamo al quadrato entrambi i membri:
\[ x^2 + (y - p)^2 = (y + p)^2 \]
Sviluppiamo i quadrati:
\[ x^2 + y^2 - 2py + p^2 = y^2 + 2py + p^2 \]
Semplifichiamo entrambi i lati:
\[ x^2 - 2py = 2py \]
Portiamo tutto a secondo membro:
\[ x^2 = 4py \]
Infine, dividiamo per \( 4p \):
\[ y = \frac{1}{4p}x^2 \]
Se poniamo \( a = \displaystyle \frac{1}{4p} \), otteniamo la forma più compatta:
\[ y = ax^2 \]
che è l'equazione canonica della parabola con vertice nell'origine \( V(0, 0) \), fuoco in \( F(0, p) \) e direttrice \( y = -p \).
In sintesi, la parabola di equazione \( y = ax^2 \) ha asse di simmetria verticale, coincidente con l'asse \( y \), e la concavità rivolta verso l'alto se \( a > 0 \), oppure verso il basso se \( a < 0 \).
Equazione Canonica di una Parabola con Asse Verticale o Orizzontale
L'equazione canonica della parabola assume forme diverse a seconda dell'orientamento dell'asse di simmetria. Distinguiamo due casi fondamentali a seconda che l'asse sia verticale o orizzontale.
Parabola con Asse Verticale
Per una parabola con asse di simmetria verticale, parallelo all'asse delle ordinate, l'equazione canonica è \( y = ax^2 \) oppure, nella forma equivalente, \( x^2 = 4py \). In questa configurazione, il coefficiente \( a = \displaystyle \frac{1}{4p} \) rappresenta il coefficiente direttore, mentre \( p \) è il parametro focale che indica la distanza dal vertice al fuoco.
Gli elementi caratteristici sono: il Vertice: \( V(0, 0) \), il Fuoco \( F\left(0, \displaystyle \frac{1}{4a}\right) \), la Direttrice: \( y = -\displaystyle\frac{1}{4a} \), l'Asse di simmetria: \( x = 0 \) (asse \( y \)) e la Concavità: verso l'alto se \( a > 0 \), verso il basso se \( a < 0 \)
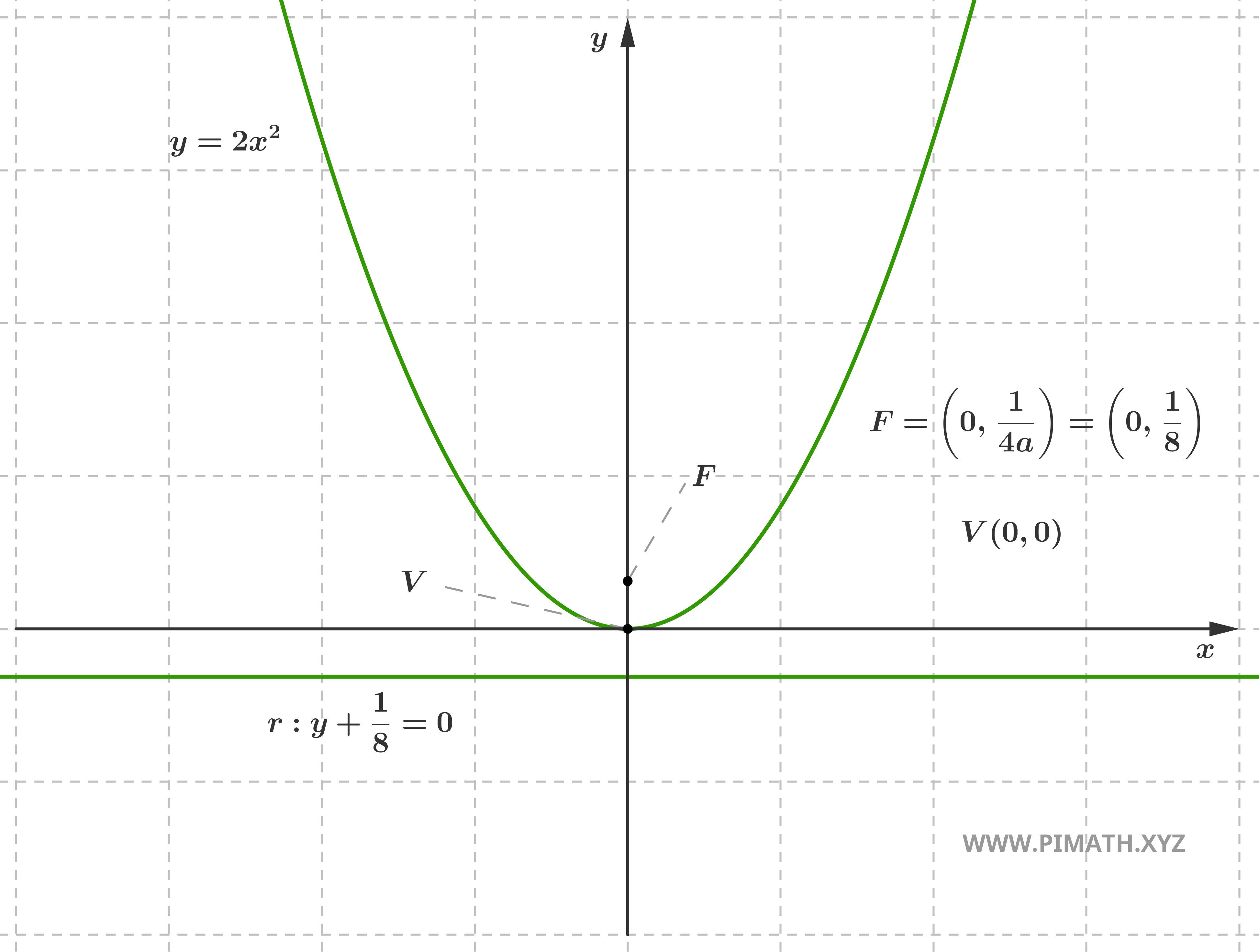
Esempio: Consideriamo la parabola \( y = 2x^2 \). Qui \( a = 2 \), quindi \( p = \displaystyle \frac{1}{4a} = \displaystyle \frac{1}{8} \). Il vertice è \( V(0, 0) \), il fuoco si trova in \( F\left(0, \displaystyle \frac{1}{8}\right) \) e la direttrice ha equazione \( y = -\displaystyle \frac{1}{8} \). Poiché \( a > 0 \), la parabola presenta concavità verso l'alto.
Parabola con Asse Orizzontale
Per una parabola con asse di simmetria orizzontale, parallelo all'asse delle ascisse, l'equazione canonica diventa \( x = ay^2 \) (se prendiamo il fuoco in \( (p, 0)\), oppure, equivalentemente, \( y^2 = 4px \). Anche in questo caso, \( a = \displaystyle \frac{1}{4p} \) è il coefficiente direttore e \( p \) rappresenta il parametro focale.
Elementi caratteristici: il Vertice: \( V(0, 0) \), il Fuoco: \( F\left(\displaystyle \frac{1}{4a}, 0\right) \), la Direttrice: \( x = -\displaystyle \frac{1}{4a} \) l'Asse di simmetria: \( y = 0 \) (asse \( x \)), e la Concavità: verso destra se \( a > 0 \), verso sinistra se \( a < 0 \).
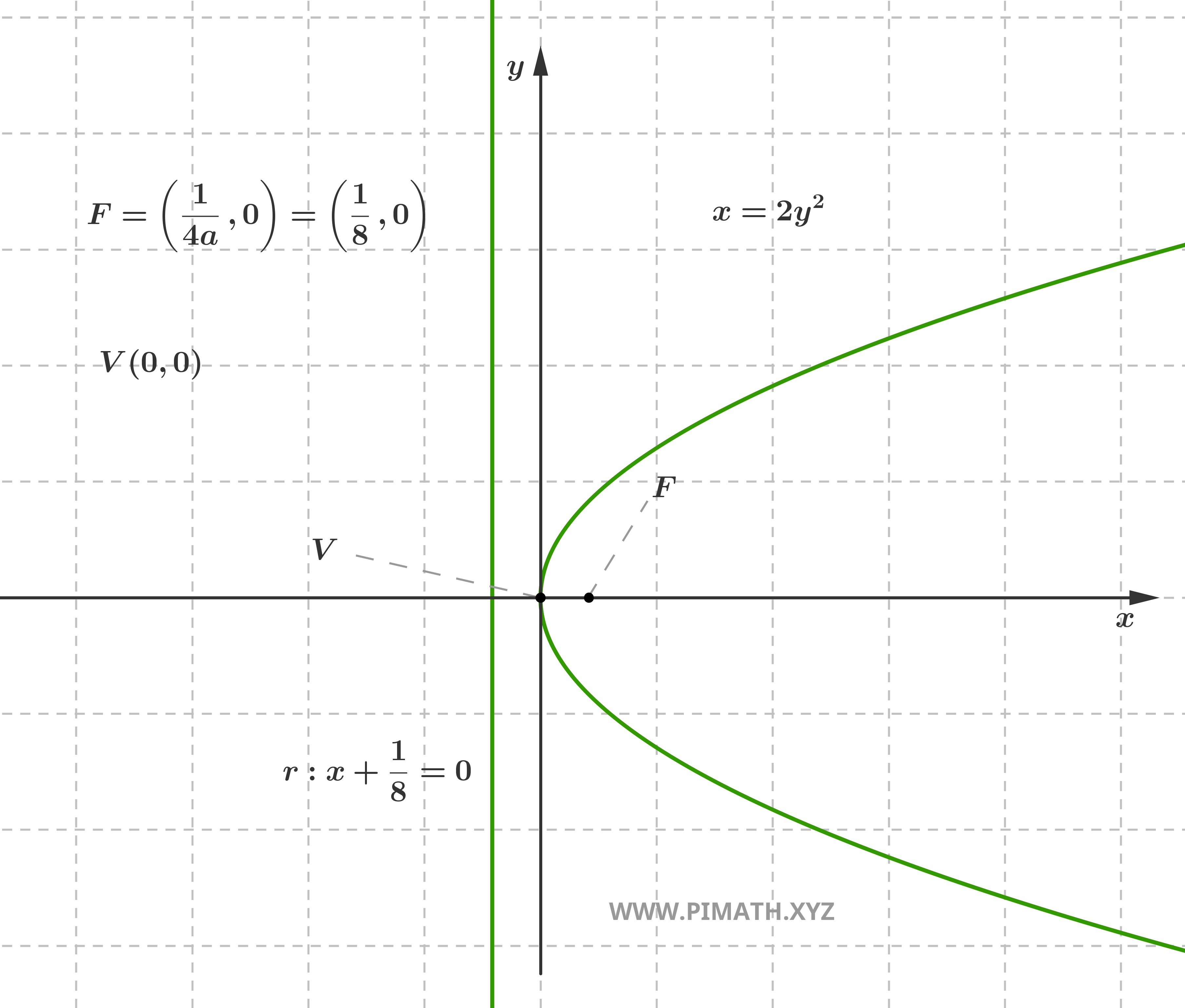
Esempio: Consideriamo la parabola \( x = \displaystyle 2y^2 \). Qui \( a = 2 \), quindi \( p = \displaystyle \frac{1}{4a} = \frac{1}{8} \). Il vertice è \( V(0, 0) \), il fuoco si trova in \( F\left(\displaystyle \frac{1}{8}, 0\right) \) e la direttrice ha equazione \( x = -\displaystyle \frac{1}{8} \). Poiché \( a > 0 \), la parabola presenta concavità verso destra.
Relazione tra i Parametri
È fondamentale comprendere la relazione che lega il coefficiente \( a \) al parametro focale \( p \), espressa dalla formula \( a = \displaystyle \frac{1}{4p} \), che equivale a \( p = \displaystyle \frac{1}{4a} \). Questa relazione ci permette di convertire facilmente da una forma all'altra dell'equazione canonica e di determinare immediatamente le caratteristiche geometriche della parabola una volta noto uno dei due parametri.
Indipendentemente dall'orientamento dell'asse di simmetria, ogni punto \( P(x, y) \) appartenente alla parabola rispetta sempre la proprietà caratteristica che definisce geometricamente questa conica: la distanza dal punto al fuoco è sempre uguale alla distanza del punto dalla direttrice.
Parabola Traslata nel Piano
Una parabola traslata si ottiene operando una trasformazione del piano cartesiano (traslazione). Questo tipo di trasformazione geometrica mantiene inalterata la forma della parabola, modificandone soltanto la posizione, e rappresenta uno degli strumenti più importanti per descrivere parabole con vertice in punti arbitrari del piano.
Trasformazione di Traslazione
La traslazione è una trasformazione geometrica che sposta ogni punto del piano di un vettore costante \( \vec{v} = (h, k) \). Se applichiamo una traslazione di vettore \( (h, k) \) alla parabola canonica \( y = ax^2 \), otteniamo una nuova parabola il cui vertice si sposta dall'origine al punto \( V(h, k) \).
Equazione della Parabola Traslata con Asse Verticale
Partendo dalla parabola canonica \( y = ax^2 \) con vertice nell'origine, una traslazione di vettore \( (h, k) \) produce la parabola traslata di equazione:
\[ y = a(x - h)^2 + k \]
Questa è la forma del vertice dell'equazione parabolica. Il parametro \( a \) mantiene il suo significato originario e determina l'apertura e l'orientamento della parabola, mentre \( h \) e \( k \) rappresentano rispettivamente la traslazione orizzontale e verticale del vertice.
Sviluppando l'espressione \( (x - h)^2 = x^2 - 2hx + h^2 \), otteniamo la forma sviluppata:
\[ y = ax^2 - 2ahx + ah^2 + k \]
Ponendo \( b = -2ah \) e \( c = ah^2 + k \), ritroviamo la forma generale \( y = ax^2 + bx + c \). Da questa relazione possiamo dedurre che \( h = -\displaystyle \frac{b}{2a} \) e \( k = c - ah^2 = c - \displaystyle \frac{b^2}{4a} \).
Elementi Geometrici della Parabola Traslata
Per una parabola traslata \( y = a(x - h)^2 + k \), tutti gli elementi geometrici caratteristici subiscono la medesima traslazione applicata alla parabola canonica: il Vertice: \( V(h, k) \), l'Asse di simmetria: \( x = h \), il Fuoco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \) e la Direttrice: \( y = k - \displaystyle \frac{1}{4a} \).
La distanza tra fuoco e direttrice rimane invariata e pari a \( 2p = \displaystyle \frac{1}{2|a|} \), così come tutte le proprietà metriche della parabola.
Esempio di Parabola Traslata
Consideriamo la parabola \( y = 2(x - 3)^2 - 5 \). Questa è una parabola ottenuta traslando la parabola canonica \( y = 2x^2 \) di \( 3 \) unità verso destra e \( 5 \) unità verso il basso.
Il vertice si trova nel punto \( V(3, -5) \), l'asse di simmetria ha equazione \( x = 3 \). Il parametro focale è \( p = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \).
Vertice, Fuoco, Direttrice e Assi di Simmetria
Gli elementi geometrici caratteristici di una parabola sono il vertice, il fuoco e la direttrice. Questi tre elementi sono collegati tra loro e determinano completamente la forma e la posizione della parabola nel piano cartesiano.
Il Vertice della Parabola
Definizione. Il vertice è il punto della parabola che realizza l'estremo assoluto (massimo o minimo, dipende dal segno di \( a \)) della funzione quadratica \( f(x) = ax^2 + bx + c \).
Le coordinate del vertice sono:
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
dove \( \Delta = b^2 - 4ac \) è il discriminante.
Dimostrazione. Trasformiamo l'equazione \( y = ax^2 + bx + c \) in forma canonica tramite completamento del quadrato:
\[ y = a\left(x^2 + \frac{b}{a}x\right) + c \]
\[ y = a\left(x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 - \left(\frac{b}{2a}\right)^2\right) + c \]
\[ y = a\left(x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a} + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a} \]
Dalla forma canonica \( y = a(x - h)^2 + k \) si legge il vertice \( V(h, k) \), quindi
\[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \]
Proprietà del vertice:
- Si trova sull'asse di simmetria \( x = -\displaystyle \frac{b}{2a} \)
- È punto di minimo se \( a > 0 \), di massimo se \( a < 0 \)
- È il punto della parabola più vicino alla direttrice
Il Fuoco della Parabola
Definizione. Il fuoco è il punto fisso tale che ogni punto della parabola è equidistante dal fuoco e dalla direttrice.
Coordinate del fuoco:
\[ F\left(-\frac{b}{2a}, -\frac{\Delta}{4a} + \frac{1}{4a}\right) \]
Dimostrazione. Nella forma canonica traslata \( Y = aX^2 \) (con \( X = x + \displaystyle \frac{b}{2a} \), \( Y = y + \displaystyle \frac{\Delta}{4a} \)), il fuoco si trova in \( \left(0, \displaystyle \frac{1}{4a}\right) \).
Per verificarlo, consideriamo un punto \( P(X_0, aX_0^2) \) sulla parabola. La distanza dal fuoco candidato \( F\left(0, \displaystyle \frac{1}{4a}\right) \) è:
\[ d(P,F) = \sqrt{X_0^2 + \left(aX_0^2 - \frac{1}{4a}\right)^2} \]
La distanza dalla direttrice candidata \( Y = -\displaystyle \frac{1}{4a} \) è:
\[ d(P,d) = \left|aX_0^2 + \frac{1}{4a}\right| \]
Per \( a > 0 \), elevando al quadrato e semplificando, si verifica che \( d(P,F) = d(P,d) \) per ogni punto \( P \) della parabola.
Tornando al sistema originale, otteniamo le coordinate indicate.
Parametro focale: La distanza dal vertice al fuoco è \( p = \displaystyle \frac{1}{4|a|} \).
La Direttrice della Parabola
Definizione. La direttrice è la retta fissa tale che ogni punto della parabola è equidistante dalla direttrice e dal fuoco.
Equazione della direttrice:
\[ y = -\frac{\Delta}{4a} - \frac{1}{4a} \]
Dimostrazione. Dalla verifica dell'equidistanza per la forma canonica, la direttrice ha equazione \( Y = -\displaystyle \frac{1}{4a} \) nel sistema traslato. Tornando al sistema originale: \( y = Y - \displaystyle \frac{\Delta}{4a} = -\displaystyle \frac{1}{4a} - \displaystyle \frac{\Delta}{4a} \).
Proprietà della direttrice:
- È perpendicolare all'asse di simmetria
- Si trova a distanza \( p = \displaystyle \frac{1}{4|a|} \) dal vertice, opposta al fuoco
- La distanza fuoco-direttrice è \( 2p = \displaystyle \frac{1}{2|a|} \)
L'Asse di Simmetria
L'asse di simmetria è la retta che passa per il vertice e il fuoco, rispetto alla quale la parabola è perfettamente simmetrica. Per una parabola con asse verticale di equazione \( y = ax^2 + bx + c \), l'asse di simmetria ha equazione \( x = -\displaystyle \frac{b}{2a} \).
Ogni punto della parabola ha un punto simmetrico rispetto all'asse di simmetria. Se \( P(x_0, y_0) \) appartiene alla parabola, allora anche il punto \( P'(2x_V - x_0, y_0) \) appartiene alla parabola, dove \( x_V \) è l'ascissa del vertice.
Relazioni tra gli Elementi
Sistema coordinato: I tre elementi formano un sistema con precise relazioni:
- Vertice e fuoco giacciono sull'asse di simmetria \( x = -\displaystyle \frac{b}{2a} \)
- La direttrice è perpendicolare all'asse di simmetria
- Vertice è equidistante da fuoco e direttrice (distanza = parametro focale \( p \))
- Se \( a > 0 \): fuoco sopra il vertice, direttrice sotto
- Se \( a < 0 \): fuoco sotto il vertice, direttrice sopra
Esempio Completo
Consideriamo la parabola di equazione \( y = 2x^2 - 8x + 3 \). Determiniamo tutti gli elementi caratteristici.
Innanzitutto, identifichiamo i coefficienti: \( a = 2 \), \( b = -8 \), \( c = 3 \). Il discriminante è \( \Delta = b^2 - 4ac = 64 - 24 = 40 \).
Il vertice ha coordinate \( V\left(-\displaystyle \frac{(-8)}{2 \cdot 2}, -\displaystyle \frac{40}{4 \cdot 2}\right) = V(2, -5) \).
L'asse di simmetria ha equazione \( x = 2 \).
Poiché \( a = 2 \), il parametro focale è \( p = \displaystyle \frac{1}{4|a|} = \displaystyle \frac{1}{4 \cdot 2} = \displaystyle \frac{1}{8} \). Poiché \( a > 0 \), la parabola ha concavità verso l'alto, quindi il fuoco si trova sopra il vertice: \( F\left(2, -5 + \displaystyle \frac{1}{8}\right) = F\left(2, -\displaystyle \frac{39}{8}\right) \).
La direttrice si trova sotto il vertice a distanza \( p \): \( y = -5 - \displaystyle \frac{1}{8} = -\displaystyle \frac{41}{8} \).
Forme Particolari
Forma canonica \( y = ax^2 \):
- Vertice: \( V(0, 0) \)
- Fuoco: \( F\left(0, \displaystyle \frac{1}{4a}\right) \)
- Direttrice: \( y = -\displaystyle \frac{1}{4a} \)
Forma traslata \( y = a(x - h)^2 + k \):
- Vertice: \( V(h, k) \)
- Fuoco: \( F\left(h, k + \displaystyle \frac{1}{4a}\right) \)
- Direttrice: \( y = k - \displaystyle \frac{1}{4a} \)
Equazione della Parabola Noti il Vertice e un Punto
Quando sono noti il vertice della parabola e un altro punto che appartiene alla curva, è possibile determinare univocamente l'equazione della parabola. Questo metodo è particolarmente utile nelle applicazioni pratiche dove si conoscono il punto di minimo o massimo di una funzione quadratica e un valore specifico assunto dalla funzione.
Forma Generale con Vertice Assegnato
Data una parabola con vertice \( V(h, k) \), l'equazione più conveniente da utilizzare è la forma del vertice, che per una parabola con asse verticale si scrive come \( y = a(x - h)^2 + k \), dove \( a \) è il parametro da determinare che controlla l'apertura e l'orientamento della parabola.
Procedimento per Parabole con Asse Verticale
Sia \( V(h, k) \) il vertice della parabola e sia \( P(x_0, y_0) \) un punto appartenente alla parabola con \( x_0 \neq h \). Sostituendo le coordinate del punto \( P \) nell'equazione \( y = a(x - h)^2 + k \), otteniamo:
\[ y_0 = a(x_0 - h)^2 + k \]
Da questa equazione possiamo ricavare direttamente il valore del parametro \( a \):
\[ a = \frac{y_0 - k}{(x_0 - h)^2} \]
Una volta determinato \( a \), l'equazione completa della parabola diventa \( y = \displaystyle \frac{y_0 - k}{(x_0 - h)^2}(x - h)^2 + k \).
Esempio Numerico - Asse Verticale
Determiniamo l'equazione della parabola con vertice \( V(3, -2) \) e passante per il punto \( P(5, 6) \).
Utilizziamo la forma del vertice \( y = a(x - 3)^2 - 2 \) e sostituiamo le coordinate del punto \( P(5, 6) \):
\[ 6 = a(5 - 3)^2 - 2 \]
\[ 6 = a \cdot 4 - 2 \]
\[ 8 = 4a \]
\[ a = 2 \]
L'equazione della parabola è quindi \( y = 2(x - 3)^2 - 2 \). Sviluppando questa espressione otteniamo \( y = 2(x^2 - 6x + 9) - 2 = 2x^2 - 12x + 18 - 2 = 2x^2 - 12x + 16 \).
Per verificare la correttezza, controlliamo che il vertice sia effettivamente \( V(3, -2) \). L'ascissa del vertice è \( x_V = -\displaystyle \frac{b}{2a} = -\displaystyle \frac{-12}{2 \cdot 2} = 3 \) e l'ordinata è \( y_V = 2 \cdot 3^2 - 12 \cdot 3 + 16 = 18 - 36 + 16 = -2 \).
Procedimento per Parabole con Asse Orizzontale
Per parabole con asse orizzontale, l'equazione in forma del vertice diventa \( x = a(y - k)^2 + h \), dove \( V(h, k) \) è il vertice. Dato un punto \( P(x_0, y_0) \) appartenente alla parabola con \( y_0 \neq k \), il parametro \( a \) si determina con:
\[ a = \frac{x_0 - h}{(y_0 - k)^2} \]
Relazione con il Parametro Focale
Una volta determinato il coefficiente \( a \), è possibile calcolare tutti gli altri elementi caratteristici della parabola. Il parametro focale è \( p = \displaystyle \frac{1}{4|a|} \), la distanza dal vertice al fuoco. Il fuoco si trova nel punto \( F(h, k + p) \) per parabole con asse verticale e \( a > 0 \), mentre si trova in \( F(h, k - p) \) se \( a < 0 \).
Esercizi Svolti sulla Parabola
Esercizio 1. Data la parabola di equazione \( y = 3x^2 - 12x + 7 \), determinare vertice, fuoco, direttrice e parametro focale.
Soluzione. Dalla forma generale \( y = ax^2 + bx + c \) identifichiamo i coefficienti \( a = 3 \), \( b = -12 \), \( c = 7 \).
Il vertice è dato dalla formula \[ V\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right) \] dove \( \Delta = b^2 - 4ac = (-12)^2 - 4(3)(7) = 144 - 84 = 60 \). Sostituendo:
\[ V\left(-\frac{-12}{2 \cdot 3}, -\frac{60}{4 \cdot 3}\right) = V\left(2, -5\right) \]
Il parametro focale è \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 3} = \frac{1}{12} \]
Poiché \( a = 3 > 0 \), la parabola ha concavità verso l'alto e il fuoco si trova sopra il vertice:
\[ F\left(2, -5 + \frac{1}{12}\right) = F\left(2, -\frac{59}{12}\right) \]
La direttrice è posizionata sotto il vertice alla stessa distanza del fuoco:
\[ y = -5 - \frac{1}{12} = -\frac{61}{12} \]
Esercizio 2. Determinare l'equazione della parabola con asse verticale che ha vertice \( V(-1, 4) \) e passa per il punto \( P(2, -5) \).
Soluzione. Utilizziamo la forma del vertice \( y = a(x - h)^2 + k \) dove \( V(h, k) = (-1, 4) \):
\[ y = a(x - (-1))^2 + 4 = a(x + 1)^2 + 4 \]
Per determinare il parametro \( a \), sostituiamo le coordinate del punto \( P(2, -5) \):
\[ -5 = a(2 + 1)^2 + 4 \]
\[ -5 = 9a + 4 \]
\[ a = \frac{-9}{9} = -1 \]
L'equazione della parabola è quindi \( y = -(x + 1)^2 + 4 \).
Sviluppando l'espressione otteniamo la forma standard:
\[ y = -(x^2 + 2x + 1) + 4 = -x^2 - 2x + 3 \]
Esercizio 3. Data la parabola con asse orizzontale \( x = 2y^2 - 8y + 6 \), determinare vertice, fuoco e direttrice.
Soluzione. Per identificare il vertice, completiamo il quadrato rispetto alla variabile \( y \):
\begin{align} x &= 2(y^2 - 4y) + 6 \\ &= 2(y^2 - 4y + 4 - 4) + 6 \\ &= 2(y - 2)^2 - 8 + 6 \\ &= 2(y - 2)^2 - 2 \end{align}
Dalla forma \( x = a(y - k)^2 + h \) leggiamo direttamente il vertice \( V(h, k) = V(-2, 2) \).
Il parametro focale è \[ p = \frac{1}{4|a|} = \frac{1}{4 \cdot 2} = \frac{1}{8} \]
Poiché \( a = 2 > 0 \), la parabola si apre verso destra e il fuoco si trova a destra del vertice:
\[ F\left(-2 + \frac{1}{8}, 2\right) = F\left(-\frac{15}{8}, 2\right) \]
La direttrice è la retta verticale posizionata a sinistra del vertice:
\[ x = -2 - \frac{1}{8} = -\frac{17}{8} \]
Esercizio 4. Data la parabola \( y = -2x^2 + 8x - 5 \), determinare l'equazione della parabola simmetrica rispetto all'asse delle ascisse. Calcolare inoltre i punti di intersezione tra le due parabole.
Soluzione. La parabola simmetrica rispetto all'asse delle ascisse si ottiene cambiando il segno della variabile \( y \). Dall'equazione originale \( y = -2x^2 + 8x - 5 \), la parabola simmetrica ha equazione:
\[ y = 2x^2 - 8x + 5 \]
Per trovare i punti di intersezione, risolviamo il sistema formato dalle due parabole:
\[ \begin{cases} y = -2x^2 + 8x - 5 \\ y = 2x^2 - 8x + 5 \end{cases} \]
Uguagliando le due espressioni:
\[ -2x^2 + 8x - 5 = 2x^2 - 8x + 5 \]
\[ -4x^2 + 16x - 10 = 0 \]
\[ -2(2x^2 - 8x + 5) = 0 \]
\[ 2x^2 - 8x + 5 = 0 \]
Applicando la formula quadratica:
\[ x = \frac{8 \pm \sqrt{64 - 40}}{4} = \frac{8 \pm \sqrt{24}}{4} = \frac{8 \pm 2\sqrt{6}}{4} = \frac{4 \pm \sqrt{6}}{2} \]
Le ordinate corrispondenti si calcolano sostituendo in una delle due equazioni:
Per \( x_1 = \displaystyle \frac{4 + \sqrt{6}}{2} \) : \( y_1 = 2\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 + \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
Per \( x_2 = \displaystyle \frac{4 - \sqrt{6}}{2} \) : \( y_2 = 2\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right)^2 - 8\left(\displaystyle \frac{4 - \sqrt{6}}{2}\right) + 5 = -\displaystyle \frac{1}{2} \)
I punti di intersezione sono:
\[ A\left(\frac{4 + \sqrt{6}}{2}, -\frac{1}{2}\right) \quad \text{e} \quad B\left(\frac{4 - \sqrt{6}}{2}, -\frac{1}{2}\right) \]
Essendo entrambi i punti alla stessa ordinata, la distanza tra essi è semplicemente:
\[ d(A,B) = \left|\frac{4 + \sqrt{6}}{2} - \frac{4 - \sqrt{6}}{2}\right| = \left|\frac{2\sqrt{6}}{2}\right| = \sqrt{6} \]
Esercizio 5. Determinare l'equazione della parabola con asse verticale che ha fuoco \( F(1, 5) \) e direttrice \( y = 3 \). Verificare se il punto \( P(3, 6) \) appartiene alla parabola.
Soluzione. Il vertice della parabola è il punto equidistante dal fuoco e dalla direttrice, situato sulla retta perpendicolare alla direttrice e passante per il fuoco. Poiché la direttrice è orizzontale, il vertice ha la stessa ascissa del fuoco e ordinata uguale alla media aritmetica:
\[ V\left(1, \frac{5 + 3}{2}\right) = V(1, 4) \]
Il parametro focale è la distanza dal vertice al fuoco:
\[ p = |5 - 4| = 1 \]
Il coefficiente della parabola è quindi:
\[ a = \frac{1}{4p} = \frac{1}{4 \cdot 1} = \frac{1}{4} \]
L'equazione della parabola nella forma del vertice è:
\[ y = \frac{1}{4}(x - 1)^2 + 4 \]
Per verificare se \( P(3, 6) \) appartiene alla parabola, sostituiamo le sue coordinate:
\[ y = \frac{1}{4}(3 - 1)^2 + 4 = \frac{1}{4} \cdot 4 + 4 = 1 + 4 = 5 \neq 6 \]
Confermiamo il risultato utilizzando la definizione geometrica della parabola. La distanza di P dal fuoco è:
\[ d(P,F) = \sqrt{(3-1)^2 + (6-5)^2} = \sqrt{4 + 1} = \sqrt{5} \]
La distanza di P dalla direttrice è:
\[ d(P, \text{direttrice}) = |6 - 3| = 3 \]
Poiché \( \sqrt{5} \neq 3 \), il punto \( P(3, 6) \) non appartiene alla parabola.

