La circonferenza è il luogo geometrico dei punti del piano che hanno distanza costante da un punto fisso, detto centro. Tale distanza costante prende il nome di raggio. La circonferenza è una curva chiusa, simmetrica rispetto al suo centro, ed è un caso particolare di conica degenere ottenuta sezionando un cono circolare retto con un piano perpendicolare all'asse del cono.
Indice
- Definizione geometrica e deduzione dell'equazione
- Equazione della circonferenza con centro nell'origine
- Equazione della circonferenza con centro generico
- Forma generale e completamento del quadrato
- Condizioni per rappresentare una circonferenza reale
- Posizione di un punto rispetto alla circonferenza
- Retta tangente alla circonferenza
- Intersezione tra due circonferenze
- Fascio di circonferenze
- Simmetrie e proprietà geometriche
- Esercizi risolti
Definizione geometrica e deduzione dell'equazione
Consideriamo un punto fisso \( C(x_0, y_0) \) nel piano cartesiano ortogonale. La circonferenza di centro \( C \) e raggio \( r > 0 \) è l'insieme dei punti \( P(x, y) \) del piano tali che:
\[ d=\text{dist}(P, C) = r \]
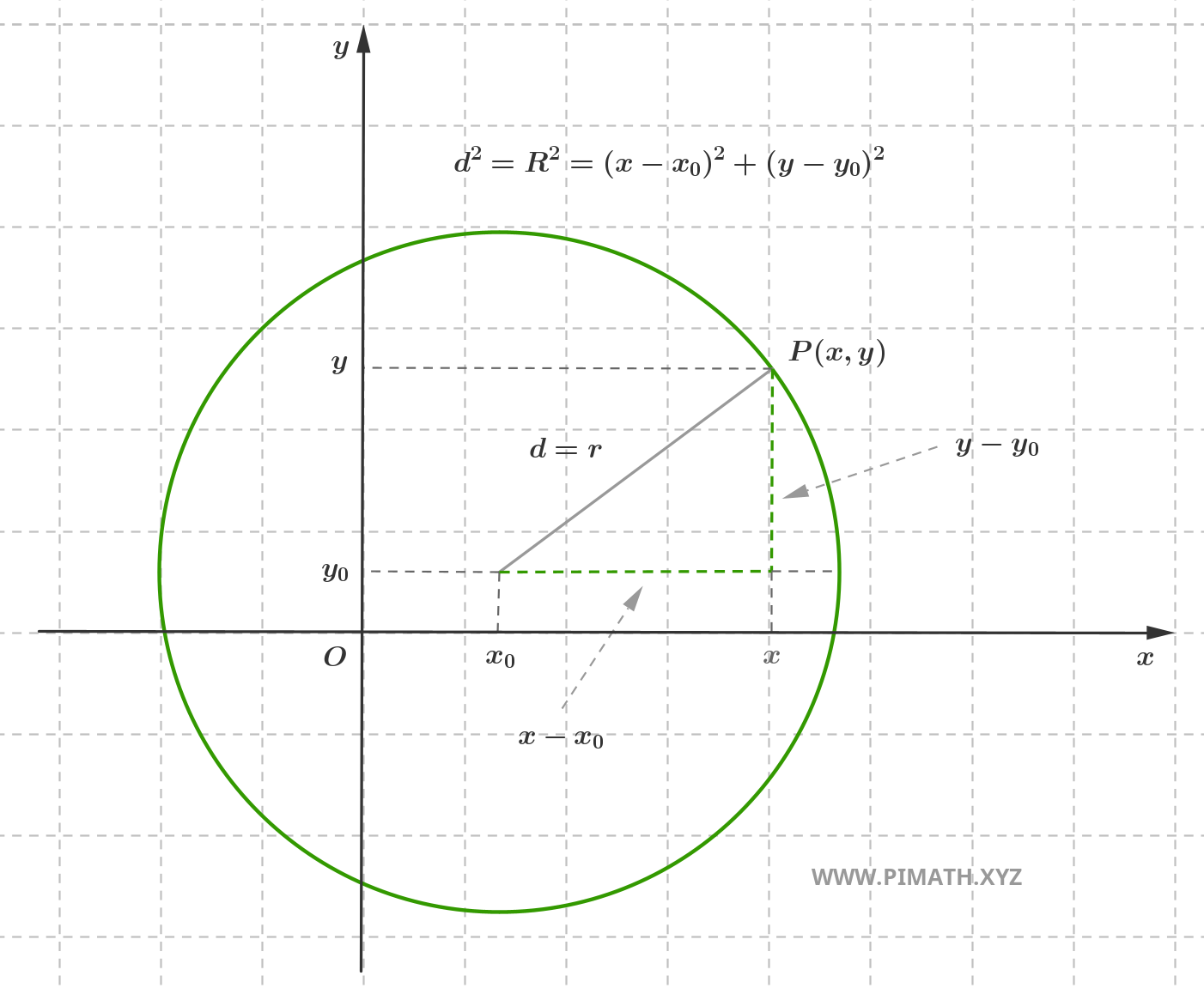
Applicando la formula della distanza euclidea tra due punti nel piano cartesiano, si ha:
\[ \text{dist}(P, C) = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]
Imponendo la condizione \( \text{dist}(P, C) = r \), otteniamo:
\[ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r \]
Elevando al quadrato entrambi i membri (operazione lecita poiché entrambi sono non negativi, essendo \( r > 0 \) per definizione):
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Questa è la forma canonica (o forma normale) dell'equazione della circonferenza con centro \( C(x_0, y_0) \) e raggio \( r \). L'equazione rappresenta tutti e soli i punti che soddisfano la condizione geometrica di appartenenza alla circonferenza.
Equazione della circonferenza con centro nell'origine
Nel caso particolare in cui il centro coincida con l'origine del sistema di riferimento, cioè \( C(0, 0) \), ponendo \( x_0 = 0 \) e \( y_0 = 0 \) nella forma canonica, l'equazione si semplifica notevolmente:
\[ x^2 + y^2 = r^2 \]
Questa è l'equazione più elementare della circonferenza e descrive l'insieme di tutti i punti equidistanti dall'origine degli assi cartesiani. L'equazione gode delle seguenti proprietà di simmetria:
- Simmetria rispetto all'asse delle ascisse: se \( (x, y) \) appartiene alla circonferenza, allora anche \( (x, -y) \) vi appartiene
- Simmetria rispetto all'asse delle ordinate: se \( (x, y) \) appartiene alla circonferenza, allora anche \( (-x, y) \) vi appartiene
- Simmetria centrale rispetto all'origine: se \( (x, y) \) appartiene alla circonferenza, allora anche \( (-x, -y) \) vi appartiene
Inoltre, tutti i diametri della circonferenza passano per l'origine e hanno lunghezza \( 2r \). Il punto \( (r, 0) \) rappresenta l'intersezione della circonferenza con il semiasse positivo delle ascisse.
Equazione della circonferenza con centro generico
Consideriamo ora il caso generale di una circonferenza con centro in un punto arbitrario \( C(x_0, y_0) \) del piano e raggio \( r > 0 \). L'equazione canonica è:
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Sviluppando i quadrati dei binomi utilizzando le identità algebriche \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \), otteniamo:
\[ x^2 - 2x \cdot x_0 + x_0^2 + y^2 - 2y \cdot y_0 + y_0^2 = r^2 \]
Riordinando i termini e portando tutte le quantità al primo membro:
\[ x^2 + y^2 - 2x_0 x - 2y_0 y + (x_0^2 + y_0^2 - r^2) = 0 \]
Introduciamo ora i parametri:
\[ D = -2x_0 \quad , \quad E = -2y_0 \quad , \quad F = x_0^2 + y_0^2 - r^2 \]
Da queste relazioni possiamo ricavare:
\[ x_0 = -\frac{D}{2} \quad , \quad y_0 = -\frac{E}{2} \quad , \quad r^2 = x_0^2 + y_0^2 - F = \frac{D^2 + E^2}{4} - F \]
Sostituendo nella forma sviluppata, otteniamo la forma generale dell'equazione della circonferenza:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Forma generale e completamento del quadrato
Data un'equazione nella forma generale:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
per ricondurla alla forma canonica e determinare centro e raggio, utilizziamo la tecnica del completamento del quadrato. Il metodo consiste nel trasformare le espressioni \( x^2 + Dx \) e \( y^2 + Ey \) in quadrati perfetti.
Per il termine in \( x \):
\[ x^2 + Dx = x^2 + Dx + \frac{D^2}{4} - \frac{D^2}{4} = \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} \]
Analogamente, per il termine in \( y \):
\[ y^2 + Ey = y^2 + Ey + \frac{E^2}{4} - \frac{E^2}{4} = \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} \]
Sostituendo nell'equazione generale:
\[ \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} + \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} + F = 0 \]
Riordinando:
\[ \left( x + \frac{D}{2} \right)^2 + \left( y + \frac{E}{2} \right)^2 = \frac{D^2 + E^2}{4} - F \]
Questa è la forma canonica, dalla quale possiamo leggere direttamente:
- Centro: \( C\left( -\displaystyle \frac{D}{2}, -\displaystyle\frac{E}{2} \right) \)
- Raggio: \( r = \sqrt{\displaystyle\frac{D^2 + E^2}{4} - F} \) (purché l'espressione sotto radice sia positiva)
Condizioni per rappresentare una circonferenza reale
Un'equazione della forma:
\[ ax^2 + by^2 + cxy + dx + ey + f = 0 \]
rappresenta una circonferenza se e solo se sono verificate le seguenti condizioni:
- Coefficienti dei termini quadratici uguali: \( a = b \neq 0 \)
- Assenza del termine misto: \( c = 0 \)
- Discriminante positivo: \( \Delta = \displaystyle \frac{d^2 + e^2}{4a^2} - \displaystyle \frac{f}{a} > 0 \)
Nel caso della forma standard \( x^2 + y^2 + Dx + Ey + F = 0 \), la condizione si riduce a:
\[ \frac{D^2 + E^2}{4} - F > 0 \quad \Leftrightarrow \quad D^2 + E^2 - 4F > 0 \]
Distinguiamo tre casi:
- Se \( D^2 + E^2 - 4F > 0 \): l'equazione rappresenta una circonferenza reale con raggio \( r = \displaystyle \frac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
- Se \( D^2 + E^2 - 4F = 0 \): l'equazione rappresenta una circonferenza degenere (un punto)
- Se \( D^2 + E^2 - 4F < 0 \): l'equazione non ha soluzioni reali (circonferenza immaginaria)
Posizione di un punto rispetto alla circonferenza
Data una circonferenza di equazione \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) e un punto \( P(x_P, y_P) \), possiamo determinare la posizione relativa del punto rispetto alla circonferenza calcolando la quantità:
\[ \delta = (x_P - x_0)^2 + (y_P - y_0)^2 - r^2 \]
Si hanno tre possibilità:
- Se \( \delta = 0 \): il punto appartiene alla circonferenza
- Se \( \delta < 0 \): il punto è interno alla circonferenza
- Se \( \delta > 0 \): il punto è esterno alla circonferenza
Equivalentemente, confrontando la distanza \( d = \sqrt{(x_P - x_0)^2 + (y_P - y_0)^2} \) del punto dal centro con il raggio:
- Se \( d = r \): punto sulla circonferenza
- Se \( d < r \): punto interno
- Se \( d > r \): punto esterno
Retta tangente alla circonferenza
Data una circonferenza di centro \( C(x_0, y_0) \) e raggio \( r \), e un punto \( P(x_1, y_1) \) appartenente alla circonferenza, l'equazione della retta tangente alla circonferenza nel punto \( P \) è:
\[ (x_1 - x_0)(x - x_0) + (y_1 - y_0)(y - y_0) = r^2 \]
Nel caso particolare di circonferenza centrata nell'origine \( x^2 + y^2 = r^2 \), l'equazione della tangente nel punto \( P(x_1, y_1) \) si semplifica in:
\[ x_1 x + y_1 y = r^2 \]
La retta tangente è perpendicolare al raggio condotto nel punto di tangenza. Questo risultato deriva dal fatto che il vettore \( \overrightarrow{CP} = (x_1 - x_0, y_1 - y_0) \) è normale alla tangente.
Tangenti da un punto esterno
Da un punto esterno \( P(x_P, y_P) \) a una circonferenza si possono condurre esattamente due rette tangenti. I punti di tangenza si ottengono risolvendo il sistema formato dall'equazione della circonferenza e dalla condizione che la distanza del centro dalla retta sia uguale al raggio.
Intersezione tra due circonferenze
Date due circonferenze:
\[ \Gamma_1: \quad x^2 + y^2 + D_1 x + E_1 y + F_1 = 0 \] \[ \Gamma_2: \quad x^2 + y^2 + D_2 x + E_2 y + F_2 = 0 \]
Per trovare i punti di intersezione, risolviamo il sistema formato dalle due equazioni. Sottraendo la seconda dalla prima, otteniamo l'equazione dell'asse radicale:
\[ (D_1 - D_2)x + (E_1 - E_2)y + (F_1 - F_2) = 0 \]
L'asse radicale è una retta che, quando le circonferenze si intersecano, passa per i due punti di intersezione. Le posizioni relative delle circonferenze dipendono dalla distanza \( d \) tra i centri e dai raggi \( r_1, r_2 \):
- Se \( d > r_1 + r_2 \): circonferenze esterne (nessuna intersezione)
- Se \( d = r_1 + r_2 \): circonferenze tangenti esternamente (un punto di intersezione)
- Se \( |r_1 - r_2| < d < r_1 + r_2 \): circonferenze secanti (due punti di intersezione)
- Se \( d = |r_1 - r_2| \): circonferenze tangenti internamente (un punto di intersezione)
- Se \( d < |r_1 - r_2| \): una circonferenza interna all'altra (nessuna intersezione)
Fascio di circonferenze
Un fascio di circonferenze è un insieme di circonferenze dipendenti da un parametro. Il fascio generato da due circonferenze \( \Gamma_1 \) e \( \Gamma_2 \) ha equazione:
\[ \lambda \Gamma_1 + \mu \Gamma_2 = 0 \]
dove \( \lambda \) e \( \mu \) sono parametri reali non entrambi nulli. Esplicitamente:
\[ \lambda(x^2 + y^2 + D_1 x + E_1 y + F_1) + \mu(x^2 + y^2 + D_2 x + E_2 y + F_2) = 0 \]
Si distinguono diversi tipi di fasci:
- Fascio ellittico: le circonferenze base non si intersecano; tutte le circonferenze del fascio sono reali
- Fascio parabolico: le circonferenze base sono tangenti; il fascio contiene rette (circonferenze degeneri)
- Fascio iperbolico: le circonferenze base si intersecano in due punti; il fascio contiene circonferenze reali e immaginarie
Simmetrie e proprietà geometriche
La circonferenza possiede notevoli proprietà di simmetria che la rendono una figura geometrica di particolare interesse:
Simmetrie
- Simmetria centrale: ogni circonferenza è simmetrica rispetto al proprio centro
- Assi di simmetria: ogni retta passante per il centro è un asse di simmetria
- Invarianza per rotazione: la circonferenza è invariante per qualsiasi rotazione attorno al centro
Proprietà metriche
- Lunghezza (circonferenza): \( C = 2\pi r \)
- Area del cerchio: \( A = \pi r^2 \)
- Angolo al centro e alla circonferenza: un angolo alla circonferenza è la metà del corrispondente angolo al centro
Esercizi risolti
Esercizio 1. Verificare se il punto \( P(3, 4) \) appartiene alla circonferenza di equazione \( x^2 + y^2 = 25 \).
Soluzione. Sostituiamo le coordinate del punto nell'equazione:
\[ 3^2 + 4^2 = 9 + 16 = 25 \]
Poiché l'uguaglianza è verificata, il punto \( P(3, 4) \) appartiene alla circonferenza. Geometricamente, ciò significa che la distanza di \( P \) dall'origine è esattamente uguale al raggio \( r = 5 \).
Esercizio 2. Determinare l'equazione della circonferenza con centro \( C(2, -3) \) e raggio \( r = 4 \).
Soluzione. Applicando la forma canonica:
\[ (x - 2)^2 + (y - (-3))^2 = 4^2 \] \[ (x - 2)^2 + (y + 3)^2 = 16 \]
Sviluppando, otteniamo la forma generale:
\[ x^2 - 4x + 4 + y^2 + 6y + 9 = 16 \] \[ x^2 + y^2 - 4x + 6y - 3 = 0 \]
Esercizio 3. Data l'equazione \( x^2 + y^2 + 6x - 8y + 5 = 0 \), determinare centro e raggio della circonferenza.
Soluzione. Completiamo i quadrati:
\[ x^2 + 6x = (x + 3)^2 - 9 \] \[ y^2 - 8y = (y - 4)^2 - 16 \]
Sostituendo:
\[ (x + 3)^2 - 9 + (y - 4)^2 - 16 + 5 = 0 \] \[ (x + 3)^2 + (y - 4)^2 = 20 \]
Quindi:
- Centro: \( C(-3, 4) \)
- Raggio: \( r = \sqrt{20} = 2\sqrt{5} \)
Esercizio 4. Trovare l'equazione della circonferenza passante per i punti \( A(1, 0) \), \( B(0, 1) \) e \( C(-1, 0) \).
Soluzione. Utilizziamo la forma generale \( x^2 + y^2 + Dx + Ey + F = 0 \) e imponiamo il passaggio per i tre punti:
Per \( A(1, 0) \), si ha
\[ 1 + 0 + D + 0 + F = 0 \implies D + F = -1 \]
Per \( B(0, 1) \), si ha
\[ 0 + 1 + 0 + E + F = 0 \implies E + F = -1 \]
Per \( C(-1, 0) \), si ha
\[ 1 + 0 - D + 0 + F = 0 \implies -D + F = -1 \]
Risolvendo il sistema:
\[ \begin{cases} D + F = -1 \\ E + F = -1 \\ -D + F = -1 \end{cases} \]
Dalla prima e terza equazione: \( D = 0 \), quindi \( F = -1 \). Dalla seconda equazione: \( E = 0 \).
L'equazione cercata è: \( x^2 + y^2 - 1 = 0 \), ovvero \( x^2 + y^2 = 1 \).
Questa è la circonferenza unitaria centrata nell'origine.
Esercizio 5. Determinare le tangenti alla circonferenza \( x^2 + y^2 = 9 \) condotte dal punto esterno \( P(5, 0) \).
Soluzione. Sia \( T(x_T, y_T) \) un punto di tangenza. La retta \( PT \) ha equazione della tangente nel punto \( T \):
\[ x_T x + y_T y = 9 \]
Poiché questa retta passa per \( P(5, 0) \):
\[ 5x_T + 0 \cdot y_T = 9 \Rightarrow x_T = \frac{9}{5} \]
Essendo \( T \) sulla circonferenza: \( x_T^2 + y_T^2 = 9 \), quindi:
\[ \left(\frac{9}{5}\right)^2 + y_T^2 = 9 \Rightarrow y_T^2 = 9 - \frac{81}{25} = \frac{144}{25} \Rightarrow y_T = \pm\frac{12}{5} \]
I punti di tangenza sono
\[ T_1\left(\frac{9}{5}, \frac{12}{5}\right) \quad \text{e} \quad T_2\left(\frac{9}{5}, -\frac{12}{5}\right) \]
Le equazioni delle tangenti sono:
\[ \frac{9}{5}x + \frac{12}{5}y = 9 \quad \implies \quad 3x + 4y = 15 \] \[ \frac{9}{5}x - \frac{12}{5}y = 9 \quad \implies \quad 3x - 4y = 15 \]

