Equazione dell'Ellisse: Formule, Dimostrazioni ed Esercizi Svolti

L’ellisse è il luogo geometrico dei punti del piano per cui la somma delle distanze da due punti fissi, detti fuochi, è costante. Ha due assi di simmetria, detti asse maggiore e asse minore. È una curva chiusa e simmetrica, con numerose applicazioni in fisica e geometria.Frelazione tra i parametri

Indice

• Come trovare l’equazione canonica dell’ellisse
• Ellisse con Semiasse Maggiore sull'Asse delle Ordinate
• Come Trovare L’equazione dell’Ellisse Traslata
• Relazione tra i parametri dell'ellisse
• Eccentricità dell’Ellisse: Definizione, Significato Geometrico e Formula
• Esercizi Svolti

Indichiamo con \( F_1(-c, 0) \) e \( F_2(c, 0) \) i due fuochi, e con \( P(x, y) \) un punto qualsiasi appartenente all’ellisse. Allora vale la seguente relazione:

\[ |PF_1| + |PF_2| = 2a \]

La costante \( 2a \) – che rappresenta la somma delle distanze \( |PF_1|\) e \(|PF_2|\) – è sempre maggiore della distanza tra i due fuochi, \( 2c \). Questo concetto è illustrato nella figura seguente:

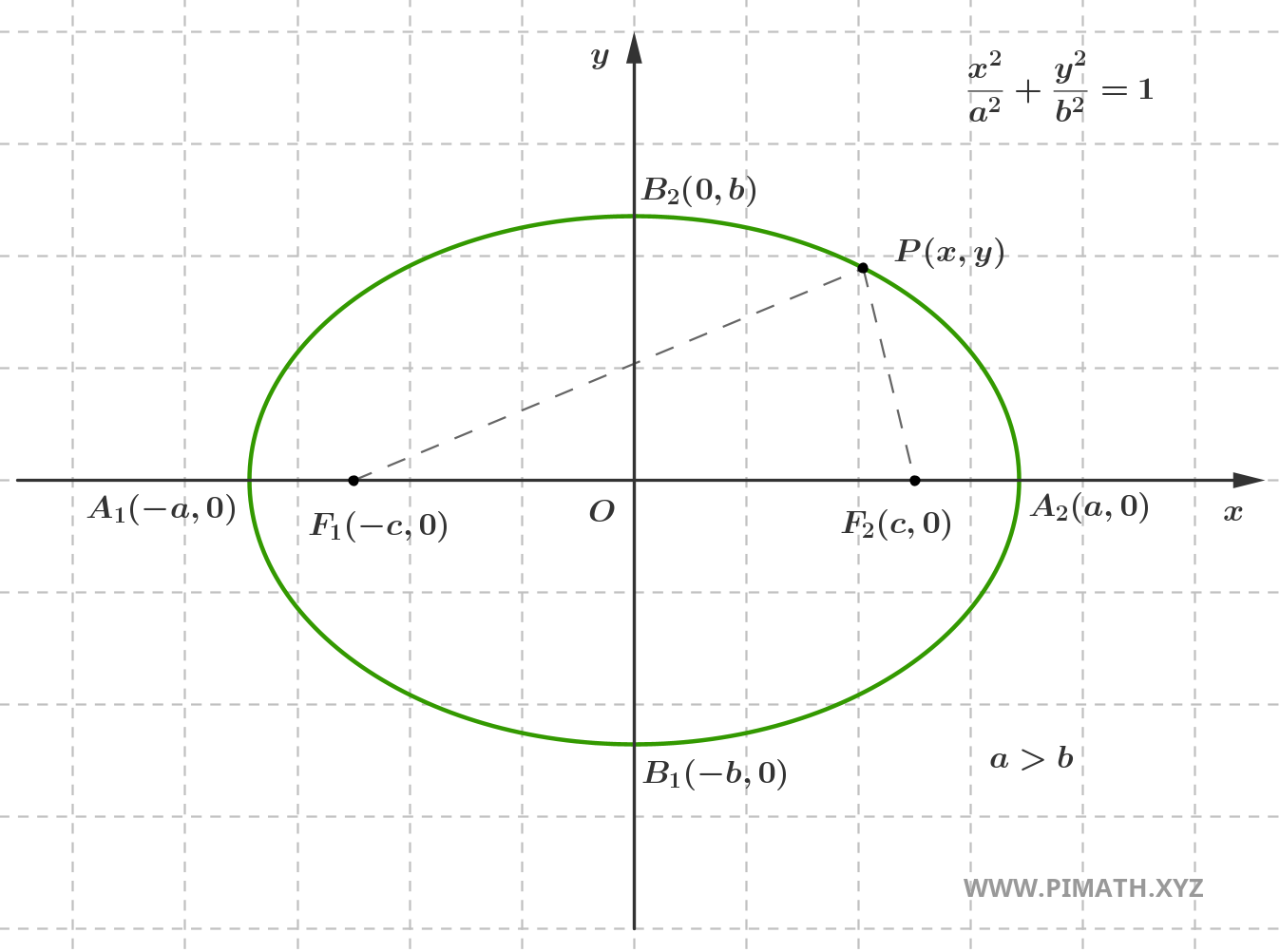
Nell’immagine, il segmento che collega il centro \( O \) al punto \( A_2 \) sull’asse orizzontale prende il nome di semiasse maggiore, e la sua lunghezza è esattamente \( a \). Il segmento verticale che collega il centro al punto \( B_2 \) viene detto semiasse minore e ha lunghezza \( b \).

La relazione che definisce l'ellisse deve naturalmente valere per tutti i punti dell'ellisse. Poniamoci nel caso particolare in cui il punto \( P(x,y) \) coincide con il punto \( B_2(0,b) \):

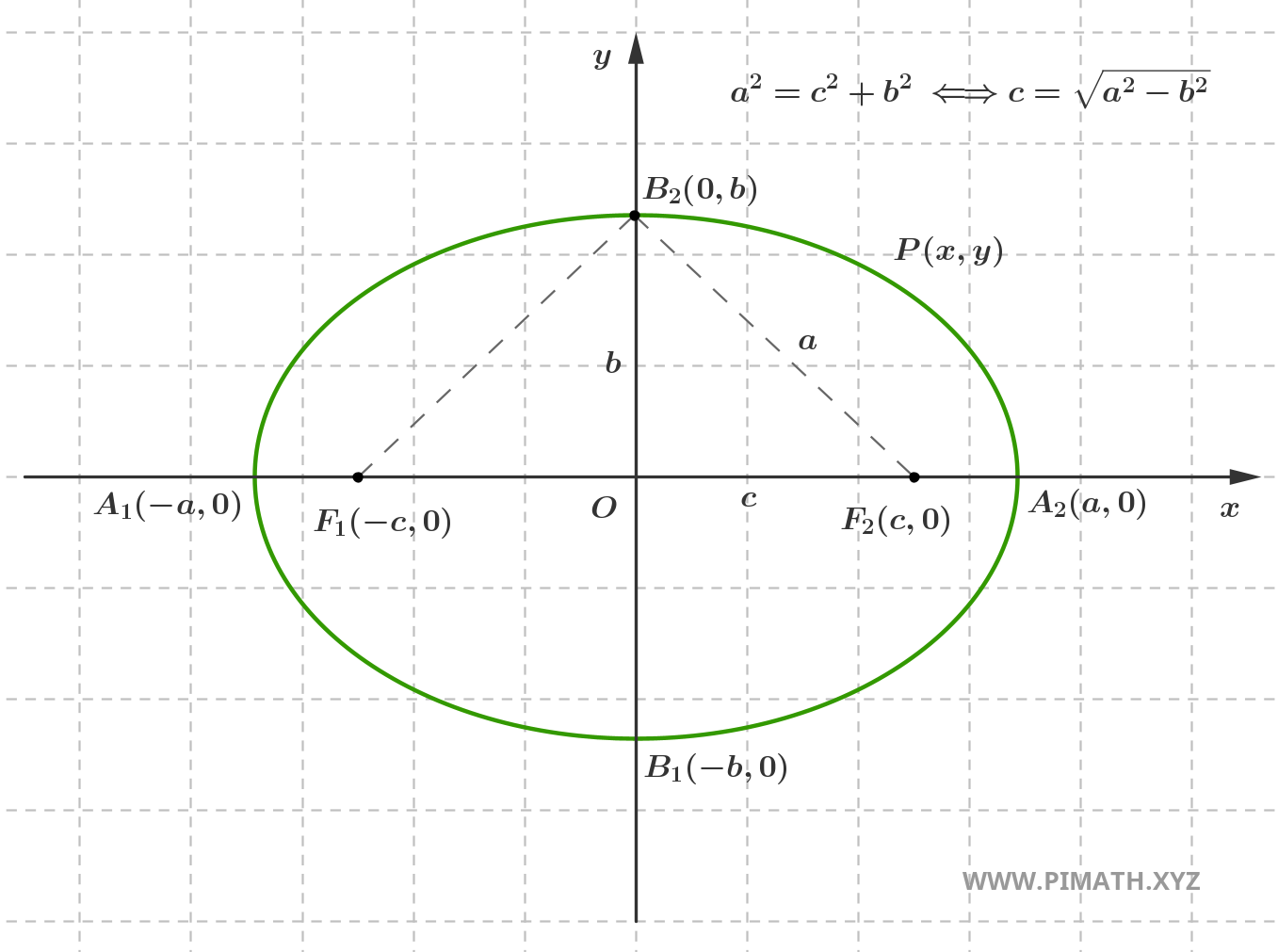
Considerando il triangolo rettangolo avente come vertici \( O(0,0) \), \( F_2(c,0) \) e \( B_2(0,b) \) e applicando il Teorema di Pitagora, si ricava che \( c=\sqrt{a^2-b^2} \), come mostrato in figura.

Consideriamo un caso semplificato in cui il centro dell’ellisse coincide con l’origine degli assi cartesiani, con i fuochi posizionati lungo l’asse orizzontale nei punti \( F_1(-c, 0) \) e \( F_2(c, 0) \).

Consideriamo un generico punto \( P(x, y) \) sul piano. Affinché \( P \) appartenga all’ellisse, deve valere la relazione:

\[ |PF_1| + |PF_2| = 2a \quad , \quad a > c \]

Ora calcoliamo le distanze tra il punto \( P(x, y) \) e ciascuno dei due fuochi:

\[ |PF_1| = \sqrt{(x + c)^2 + y^2} \quad \text{e} \quad |PF_2| = \sqrt{(x - c)^2 + y^2} \]

Sostituendo queste espressioni nella condizione iniziale otteniamo:

\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \]

Per eliminare uno dei radicali, portiamo \( \sqrt{(x + c)^2 + y^2} \) a secondo membro:

\[ \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2} \]

Eleviamo al quadrato entrambi i membri per eliminare la radice:

\[ (x - c)^2 + y^2 = \left(2a - \sqrt{(x + c)^2 + y^2} \right)^2 \]

Sviluppiamo il quadrato del secondo membro:

\[ (x - c)^2 + y^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]

Eliminiamo il termine \( y^2 \) presente su entrambi i lati e sviluppiamo i quadrati:

\[ x^2 - 2cx + c^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 \]

Semplificando entrambi i membri:

\[ -4cx = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} \]

Dividiamo entrambi i membri per 4:

\[ -cx = a^2 - a\sqrt{(x + c)^2 + y^2} \]

Portiamo tutti i termini con la radice a primo membro:

\[ a\sqrt{(x + c)^2 + y^2} = a^2 + cx \]

Eleviamo di nuovo al quadrato entrambi i membri:

\[ a^2[(x + c)^2 + y^2] = (a^2 + cx)^2 \]

Sviluppiamo entrambi i lati:

\[ a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2 \]

Sviluppiamo completamente:

\[ a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2 \]

Semplifichiamo i termini comuni da entrambi i lati:

\[ a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2 \]

Raccogliamo i termini simili:

\[ x^2(a^2 - c^2) + a^2y^2 = a^2(a^2 - c^2) \]

Poiché \( a > c \), la quantità \( a^2 - c^2 \) è positiva. Indichiamola con \( b^2 \), così da ottenere:

\[ b^2 = a^2 - c^2 \]

Sostituendo, otteniamo:

\[ x^2b^2 + a^2y^2 = a^2b^2 \]

Dividiamo entrambi i membri per \( a^2b^2 \) per isolare i termini:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , \quad a > b \]

Questa è la forma canonica dell’equazione dell’ellisse con centro nell’origine e fuochi sull’asse delle ascisse. L'equazione è simmetrica rispetto ad entrambi gli assi cartesiani e rispetto all'origine.

Introduciamo un po' di nomenclatura. La retta che contiene i fuochi si chiama asse focale, mentre il punto di intersezione tra gli assi è il centro dell’ellisse.

• I punti in cui l’ellisse interseca l’asse focale e la retta ad esso perpendicolare passante per il centro si chiamano vertici dell’ellisse.
• Il segmento \( A_1A_2 \) prende il nome di asse maggiore, mentre il segmento \( B_1B_2 \) è detto asse minore.
• Si definisce semiasse maggiore la lunghezza \( a \), e semiasse minore la lunghezza \( b \).

Se vogliamo descrivere un’ellisse che ha il semiasse maggiore verticale, cioè orientato lungo l’asse delle ordinate, dobbiamo semplicemente scambiare il ruolo di \( a \) e \( b \) nell’equazione canonica che descrive l'ellisse con semiasse maggiore sull'asse delle ascisse, come mostrato in figura:

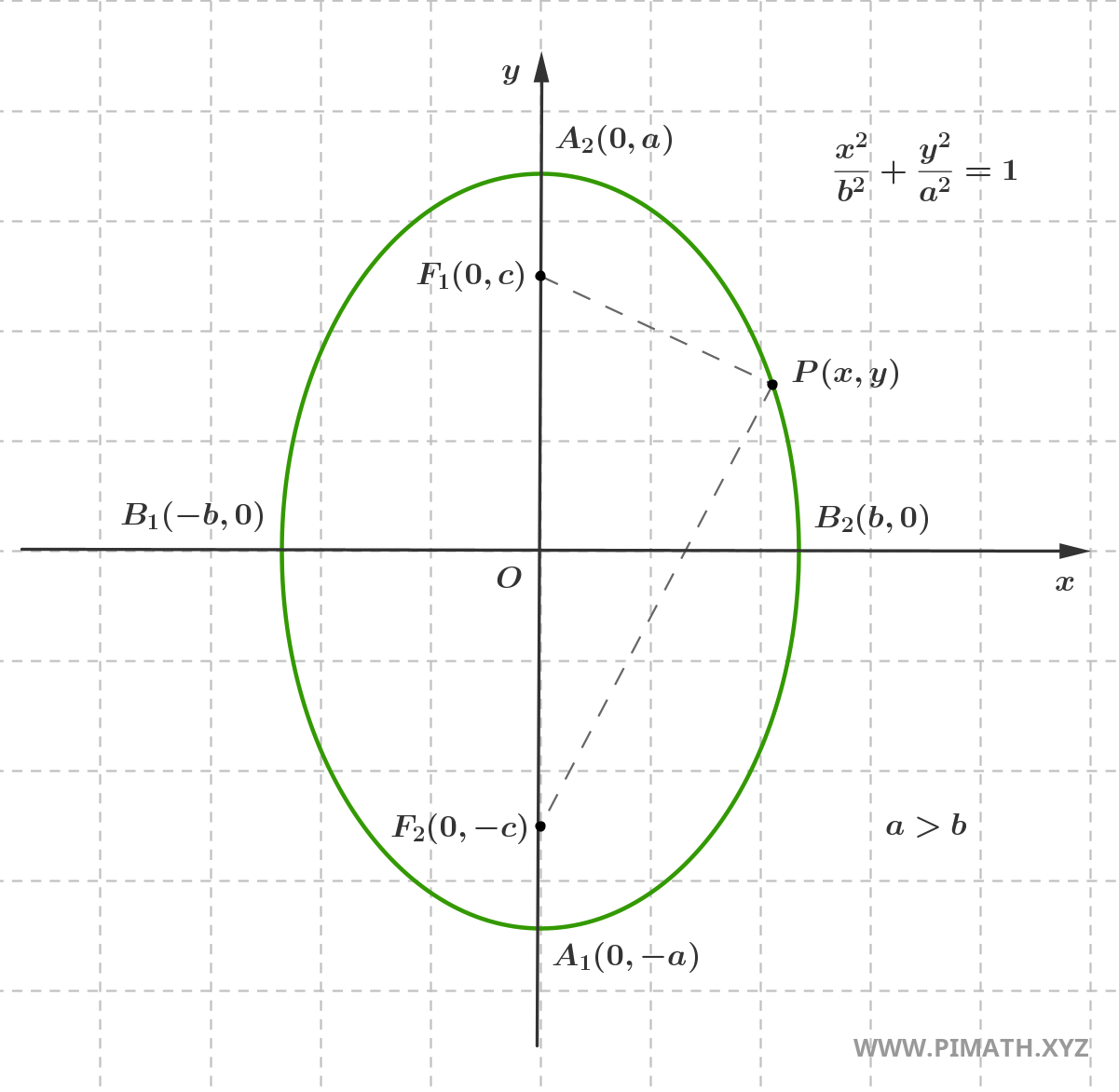
In questo caso, imponendo \( |PF_1| + |PF_2| = 2a \) e con analoghi passaggi algebrici, l’equazione dell’ellisse diventa:

\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \]

Questo cambiamento riflette una rotazione dell’ellisse di 90 gradi rispetto all’asse \(x\). La forma dell’equazione rimane la stessa, ma l’asse lungo il quale si sviluppa l’ellisse cambia.

Anche in questo caso il centro dell’ellisse resta nell’origine e la definizione geometrica resta valida: per ogni punto \( P(x, y) \) sull’ellisse, la somma delle distanze dai fuochi (che ora sono posizionati lungo l’asse \( y \)) è sempre pari a \( 2a \).

Finora abbiamo considerato un’ellisse con centro nell’origine e fuochi sull’asse delle ascisse. Tuttavia, un’ellisse può trovarsi in qualsiasi punto del piano. In tal caso, si parla di ellisse traslata.

Supponiamo che il centro dell’ellisse sia nel punto \( C(x_0, y_0) \). L’equazione canonica si modifica di conseguenza, traslando le coordinate.

Per l'equazione dell'ellisse traslata, è fondamentale distinguere quale sia il semiasse maggiore e quale il semiasse minore. A seconda dell'orientamento dell'ellisse rispetto agli assi cartesiani, l'equazione canonica traslata assume forme leggermente diverse:

Ellisse Traslata Orizzontale

L'asse maggiore è parallelo all'asse \( x \), quindi i fuochi sono lungo la retta \( y = y_0 \)

In questo caso, il semiasse maggiore \( a \) è il valore sotto il termine \( (x - x_0)^2 \), e il semiasse minore \( b \) è il valore sotto il termine \( (y - y_0)^2 \).

\[ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 \quad , \quad a > b \]

Ellisse Traslata Verticale

L'asse maggiore è parallelo all'asse \( y \), quindi i fuochi sono lungo la retta \( x = x_0 \)

In questo caso, il semiasse maggiore \( a \) è il valore sotto il termine \( (y - y_0)^2 \), e il semiasse minore \( b \) è il valore sotto il termine \( (x - x_0)^2 \).

\[ \frac{(x - x_0)^2}{b^2} + \frac{(y - y_0)^2}{a^2} = 1 \quad , \quad a > b \]

Nota: I fuochi non si trovano più sugli assi cartesiani \( x \) o \( y \), ma su rette parallele a questi, passanti per il centro \( (x_0, y_0) \).

Relazione tra i parametri dell'ellisse

Nel caso di un'ellisse con centro nell'origine e assi paralleli agli assi cartesiani, la relazione tra i parametri principali è data da una formula fondamentale che lega il semiasse maggiore \( a \), il semiasse minore \( b \) e la distanza dei fuochi dal centro \( c \).

La formula è la seguente:

\[ c^2 = a^2 - b^2 \]

Dunque, la distanza dei fuochi dal centro si può calcolare come:

\[ c = \sqrt{a^2 - b^2} \]

Questa relazione è valida per tutte le ellissi con centro nell'origine e assi allineati agli assi cartesiani, dove \( a > b \). Il semiasse maggiore è sempre associato all'asse con il denominatore più grande nell'equazione canonica dell'ellisse:

\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , a > b \quad \text{(se l'asse maggiore è orizzontale)} \]

Invece:

\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \quad \text{(se l'asse maggiore è verticale)} \]

In tal caso, \( c^2 = a^2 - b^2 \) e dunque \( c = \sqrt{a^2 - b^2} \). Conoscere queste relazioni consente di calcolare rapidamente la posizione dei fuochi e di comprendere meglio la geometria dell'ellisse.

Eccentricità dell’Ellisse: Definizione, Significato Geometrico e Formula

L’eccentricità è una misura fondamentale che ci permette di capire quanto un’ellisse si discosti da un cerchio. Ogni ellisse ha due fuochi: sono due punti interni tali che la somma delle distanze da un qualsiasi punto dell’ellisse ai due fuochi è costante. L’eccentricità, indicata con la lettera \( e \), è un numero che varia da \( 0 \) a \( 1 \) e descrive la forma dell’ellisse.

Definizione di Eccentricità

L'eccentricità \( e \) non è un dato che si sceglie a piacere, ma un valore che emerge naturalmente dalle proprietà geometriche dell'ellisse. In particolare, se \( a \) è la lunghezza del semiasse maggiore e \( b \) quella del semiasse minore, allora la distanza \( c \) tra il centro e uno dei fuochi è: \[c = \sqrt{a^2 - b^2}\] Con \( a > b \), l'eccentricità è sempre data dalla seguente formula: \[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1-\frac{b^2}{a^2}}\] Questa formula è valida sia quando l'asse maggiore è orizzontale che quando è verticale, poiché \( a \) rappresenta sempre il semiasse maggiore indipendentemente dall'orientamento dell'ellisse.

Significato Geometrico dell’Eccentricità

Quando l’eccentricità è pari a zero, cioè \( e = 0 \), significa che i due fuochi coincidono nel centro dell’ellisse. In questo caso l’ellisse è in realtà un circonferenza, perché tutti i raggi (cioè i segmenti che uniscono il centro a un punto della curva) hanno la stessa lunghezza: \( a = b \).

Quando invece l’eccentricità è un numero compreso tra \( 0 \) e \( 1 \), cioè \( 0 < e < 1 \), l’ellisse è allungata. Maggiore è il valore di \( e \), più i fuochi si allontanano dal centro e più l'ellisse appare allungata lungo l'asse maggiore e compressa lungo l'asse minore.

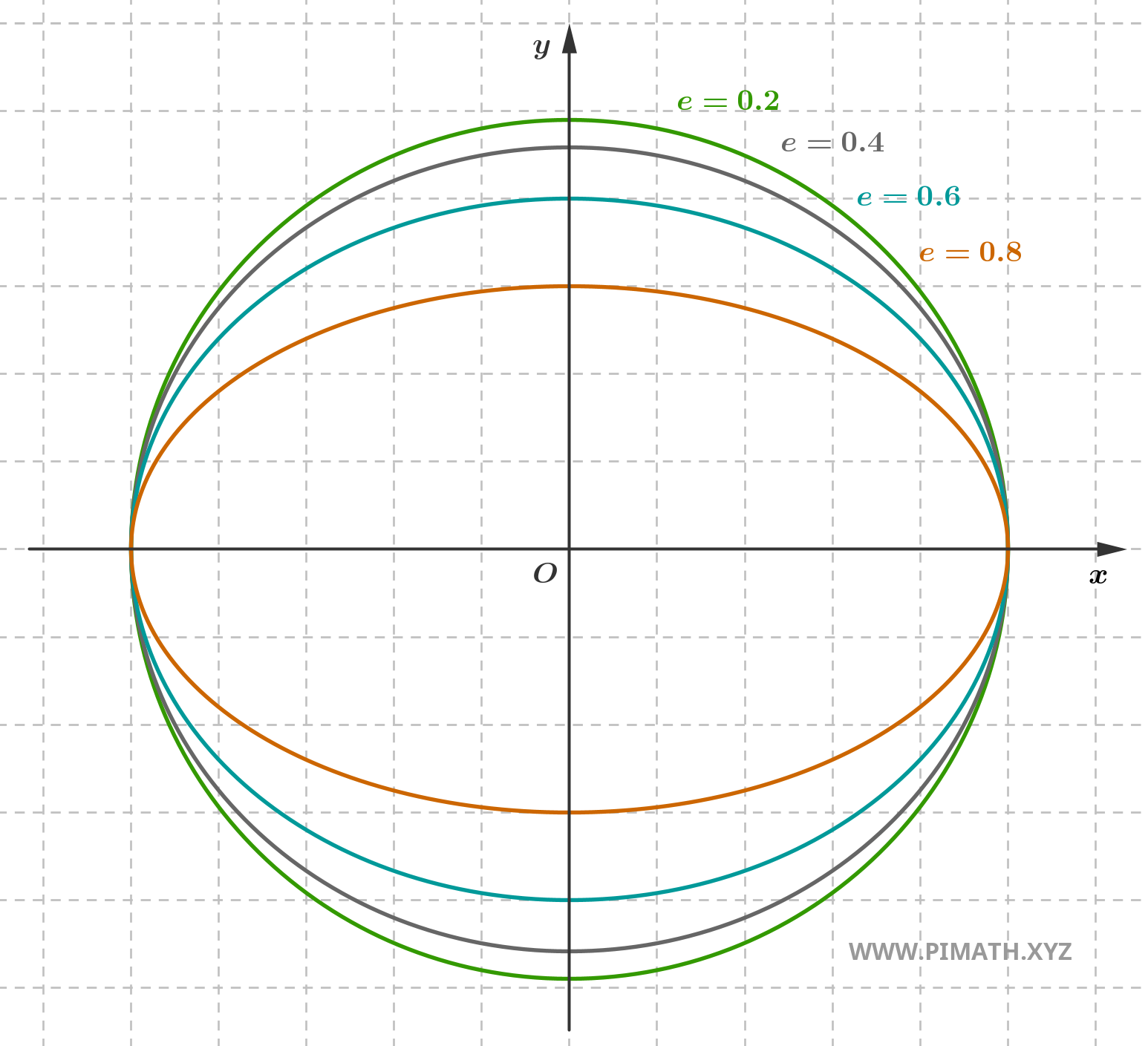
Infine, quando \( e \) si avvicina a \( 1 \), la forma dell’ellisse diventa estremamente allungata e i fuochi sono molto distanti dal centro.

Per esempio, consideriamo un’ellisse con semiasse maggiore \( a = 5 \) e semiasse minore \( b = 3 \).

Calcoliamo prima la distanza dei fuochi dal centro:

\[c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4\]

A questo punto possiamo calcolare l’eccentricità:

\[e = \frac{4}{5} = 0,8\]

Il valore che abbiamo trovato indica che l’ellisse è piuttosto schiacciata e i fuochi sono ben distanti dal centro. Ecco il grafico:

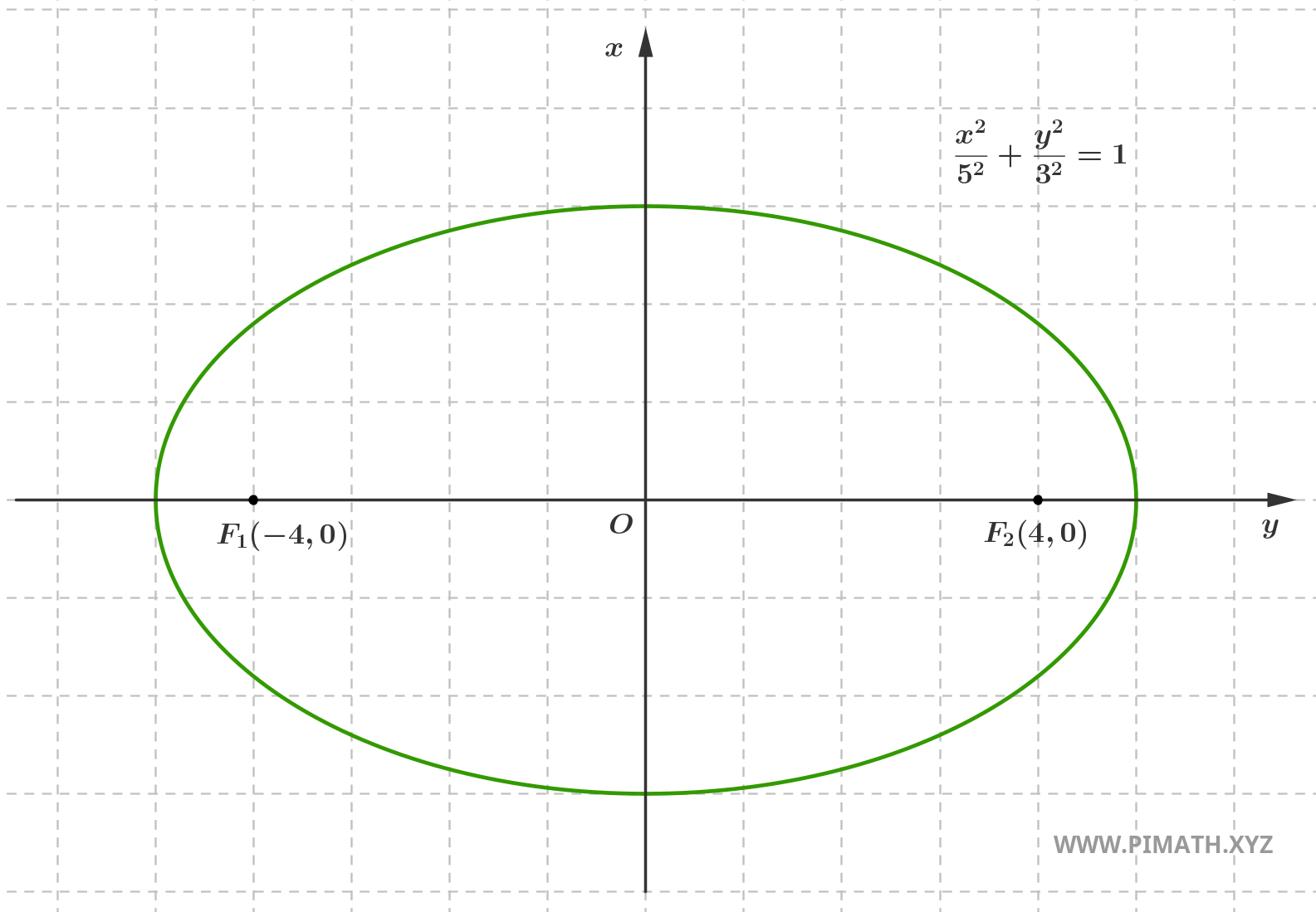
L’eccentricità dell’ellisse è un concetto che mette in relazione la posizione dei fuochi con la forma complessiva della curva. Non è solo una formula da memorizzare, ma uno strumento utile per intuire visivamente quanto l’ellisse sia vicina a un cerchio o quanto sia allungata. Ricorda: più \( e \) è vicino a zero, più l’ellisse è simile a un cerchio. Più \( e \) è vicino a \( 1 \), più è schiacciata e i fuochi sono lontani.

Esercizi Svolti

Esercizio 1. Verificare se il punto \( P(3, 2) \) appartiene all'ellisse di equazione:
\[ \frac{x^2}{9} + \frac{y^2}{4} = 1 \]

Soluzione. Sostituiamo \( x = 3 \), \( y = 2 \):

\[ \frac{3^2}{9} + \frac{2^2}{4} = \frac{9}{9} + \frac{4}{4} = 1 + 1 = 2 \neq 1 \]

Questo significa che il punto non appartiene all'ellisse.

Esercizio 2. Un'ellisse ha centro nell'origine, asse maggiore orizzontale, semiasse maggiore \( a = 5 \) e semiasse minore \( b = 3 \). Trovare l'equazione dell'ellisse.

Soluzione. L'equazione canonica è
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{9} = 1 \]

Esercizio 3. Determina la posizione dei fuochi dell'ellisse di equazione:

\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]

Trovare la distanza dei fuochi \( c \). 

Soluzione. Dall'equazione \( \displaystyle \frac{x^2}{16} + \displaystyle \frac{y^2}{9} = 1 \), identifichiamo che il termine maggiore (16) è sotto \( x^2 \), quindi l'asse maggiore è orizzontale.
Secondo la nostra convenzione: \( a^2 = 16 \), \( b^2 = 9 \), quindi \( a = 4 \), \( b = 3 \).
Calcoliamo la distanza dei fuochi \( c \) usando:

\[ c^2 = a^2 - b^2 = 16 - 9 = 7 \Rightarrow c = \sqrt{7} \]

I fuochi si trovano nei punti \( F_1(-\sqrt{7}, 0) \), \( F_2(\sqrt{7}, 0) \).

Esercizio 4. Scrivi l'equazione canonica dell'ellisse con centro nell'origine, asse maggiore verticale, sapendo che i vertici si trovano nei punti \( (0, \pm 6) \) e i fuochi si trovano nei punti \( (0, \pm 4) \).

Soluzione. Se i vertici sono in \( (0, \pm 6) \), allora il semiasse maggiore è \( a = 6 \), quindi \( a^2 = 36 \).
I fuochi sono in \( (0, \pm 4) \), quindi \( c = 4 \), quindi \( c^2 = 16 \).
Calcoliamo:

\[ b^2 = a^2 - c^2 = 36 - 16 = 20 \]

L'equazione dell'ellisse, con asse maggiore verticale, è: \[ \displaystyle \frac{x^2}{b^2} + \displaystyle \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{20} + \frac{y^2}{36} = 1 \]

Esercizio 5. Un'ellisse ha i fuochi nei punti \( F_1(-3,0) \) e \( F_2(3,0) \), e passa per il punto \( P(4,1) \). Trova l'equazione canonica dell'ellisse.

Soluzione. I fuochi sono \( F_1(-3, 0) \), \( F_2(3, 0) \). Allora \( c = 3 \), quindi \( c^2 = 9 \).
Il punto \( P(4, 1) \) appartiene all'ellisse. Per definizione: \[ |PF_1| + |PF_2| = 2a \] Calcoliamo: \[ |PF_1| = \sqrt{(4 - (-3))^2 + (1 - 0)^2} = \sqrt{7^2 + 1^2} = \sqrt{49 + 1} = \sqrt{50} = 5\sqrt{2} \] \[ |PF_2| = \sqrt{(4 - 3)^2 + (1 - 0)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \] \[ \Rightarrow |PF_1| + |PF_2| = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \] \[ \Rightarrow 2a = 6\sqrt{2} \Rightarrow a = 3\sqrt{2} \Rightarrow a^2 = (3\sqrt{2})^2 = 9 \cdot 2 = 18 \] \[ b^2 = a^2 - c^2 = 18 - 9 = 9 \] L'equazione dell'ellisse è quindi: \[ \frac{x^2}{18} + \frac{y^2}{9} = 1 \]