Un'equazione di primo grado è un polinomio di primo grado eguagliato a zero. In generale, un'equazione è di primo grado se può essere scritta nella forma canonica:
\[ ax + b = 0 \quad \text{con} \quad a \neq 0 \]
La parte che sta a sinistra del segno di uguaglianza prende il nome di primo membro, mentre quella che sta a destra prende il nome di secondo membro.
Indice
- Come risolvere un'equazione di primo grado
- Primo principio di equivalenza
- Secondo principio di equivalenza
- Esercizi Svolti
- Errori comuni da evitare
- Significato Geometrico
Come risolvere un'equazione di primo grado
Risolvere un'equazione di primo grado significa trovare il valore che, sostituito all'incognita \( x \), soddisfa l'equazione. Questo equivale a dire che il valore (soluzione dell'equazione) deve rendere vera l'uguaglianza. Il processo di risoluzione prevede alcuni passaggi, detti principi di equivalenza per le equazioni.
Primo principio di equivalenza
Il primo principio di equivalenza afferma che, addizionando o sottraendo ad ambo i membri di una equazione una quantità o una espressione algebrica, l'insieme delle soluzioni non cambia.
Grazie a questo principio, possiamo sottrarre la quantità \( -b \) ad ambo i membri:
\[ ax = -b \]
Nota che sommare o sottrarre una quantità ad ambo i membri equivale a "portare" da un membro all'altro purchè venga cambiato il segno. Per adesso abbiamo portato al secondo membro \( b \) cambiato di segno, dunque \( -b \).
Secondo principio di equivalenza
Il secondo principio di equivalenza afferma che, moltiplicando o dividendo per uno stesso numero diverso da zero, l'insieme delle soluzioni dell'equazione non cambia.
Applicando questo principio all'equazione equivalente \( ax = -b \), quindi dividendo per il numero \( a \neq 0 \) ad ambo i membri, otteniamo:
\[ x = -\frac{b}{a} \]
È importante sottolineare che \( a \) deve essere diverso da zero affinché l'equazione abbia senso. Infatti, se \( a = 0 \) l'equazione diventerebbe \( 0 \cdot x + b = 0 \) e quindi \( b = 0 \), che non rappresenta un'equazione in \( x \) e sarebbe impossibile se \( b \neq 0 \).
D'ora in poi l'obiettivo sarà isolare la variabile \( x \) al primo membro, oppure al secondo (non cambia niente).
Esercizi Svolti
Esercizio 1. Risolvere l'equazione \( 3x - 1 = 0\).
Soluzione. Portiamo \( -1 \) al secondo membro (cambiandone il segno):
\[ 3x = 1 \]
Infine, dividendo entrambi i membri per \( 3 \) otteniamo la soluzione cercata:
\[ x = \frac{1}{3} \]
Verifica. Per verificare che è la soluzione corretta, sostituiamo il valore trovato nell'equazione di partenza. Otteniamo:
\[ 3 \cdot \frac{1}{3} - 1 = 1 - 1 = 0 \]
Quindi la soluzione è corretta.
Esercizio 2: Risolvere l'equazione di primo grado \(\displaystyle\frac{1}{2}(x-1)=-x+1\).
Soluzione. Iniziamo isolando l'incognita \( x \) al primo membro:
\[ \frac{1}{2}(x - 1) = -x + 1 \implies \frac{x}{2} - \frac{1}{2} = -x + 1 \]
Ora sommiamo \(x\) a entrambi i membri dell'equazione:
\[ \frac{x}{2} + x - \frac{1}{2} = 1 \]
Semplifichiamo trasformando \(x\) in un termine con denominatore comune:
\[ \frac{x}{2} + \frac{2x}{2} - \frac{1}{2} = 1 \implies \frac{3x}{2} - \frac{1}{2} = 1 \]
Aggiungiamo \(\displaystyle\frac{1}{2}\) a entrambi i membri:
\[ \frac{3x}{2} = \frac{3}{2} \]
Ora moltiplichiamo entrambi i membri per \(\displaystyle\frac{2}{3}\) per risolvere per \(x\):
\[ x = 1 \]
Quindi, la soluzione è \( x = 1 \).
Verifica. Come prima, sostituiamo \( x = 1 \) nell'equazione di partenza:
\[ \frac{1}{2}(x - 1) = -x + 1 \]
Quando \( x = 1 \), otteniamo:
\[ \frac{1}{2}(1 - 1) = -1 + 1 \]
Calcoliamo entrambi i membri:
\[ \frac{1}{2} \cdot 0 = 0 \quad \text{e} \quad -1 + 1 = 0 \]
I due membri sono uguali, quindi la soluzione è corretta.
Esercizio 3. Risolvere l'equazione \( 5(x - 2) - 3(2x + 1) = 7 - 4x \)
Soluzione. Applichiamo la proprietà distributiva:
\[ 5x - 10 - 6x - 3 = 7 - 4x \]
\[ -x - 13 = 7 - 4x \]
Portiamo i termini con \(x\) al primo membro e i termini costanti al secondo membro:
\[ -x + 4x = 7 + 13 \]
\[ 3x = 20 \]
Dividiamo entrambi i membri per 3:
\[ x = \frac{20}{3} \]
Verifica. Sostituiamo \(\displaystyle x = \frac{20}{3}\) nell'equazione di partenza:
\[ 5\left(\frac{20}{3} - 2\right) - 3\left(2\cdot\frac{20}{3} + 1\right) = 7 - 4\cdot\frac{20}{3} \]
Calcoliamo il primo membro:
\[ 5\left(\frac{20}{3} - \frac{6}{3}\right) - 3\left(\frac{40}{3} + \frac{3}{3}\right) = 5\cdot\frac{14}{3} - 3\cdot\frac{43}{3} = \frac{70}{3} - \frac{129}{3} = -\frac{59}{3} \]
Calcoliamo il secondo membro:
\[ 7 - 4\cdot\frac{20}{3} = \frac{21}{3} - \frac{80}{3} = -\frac{59}{3} \]
I due membri sono uguali, quindi la soluzione è verificata:
\[ x = \frac{20}{3} \]
Errori comuni da evitare
Quando si risolvono equazioni di primo grado, è importante fare attenzione ad alcuni errori frequenti:
Errore nel cambio di segno: Quando si sposta un termine da un membro all'altro, bisogna ricordare di cambiarne il segno. Per esempio, nell'equazione \(2x + 3 = 5\), spostando il \( 3 \) si ottiene \(2x = 5 - 3\) e non \(2x = 5 + 3\).
Distribuzione incompleta: Quando si ha un'espressione del tipo \(3(x + 2)\), il coefficiente \( 3 \) deve essere moltiplicato per tutti i termini dentro la parentesi. Un errore comune è scrivere \(3x + 2\) invece del corretto \(3x + 6\).
Errori con le frazioni: Quando si ha un'equazione come \(\displaystyle \frac{x}{2} = 3\), per isolare \(x\) bisogna moltiplicare entrambi i membri per 2, ottenendo \(x = 6\). È sbagliato scrivere \(x = \displaystyle \frac{3}{2}\).
Semplificazione imprecisa: In un'equazione come \(2x - x = 5\), non bisogna dimenticare di semplificare i termini simili prima di procedere. La forma corretta è \(x = 5\).
Verifica mancante: Saltare il passaggio della verifica può portare a non accorgersi di eventuali errori di calcolo. È sempre consigliabile sostituire la soluzione trovata nell'equazione originale per confermare che sia corretta.
Significato Geometrico
Risolvere un'equazione di primo grado \( ax + b = 0\) significa trovare il valore in corrispondenza del quale la retta di equazione
\[ y = ax + b \]
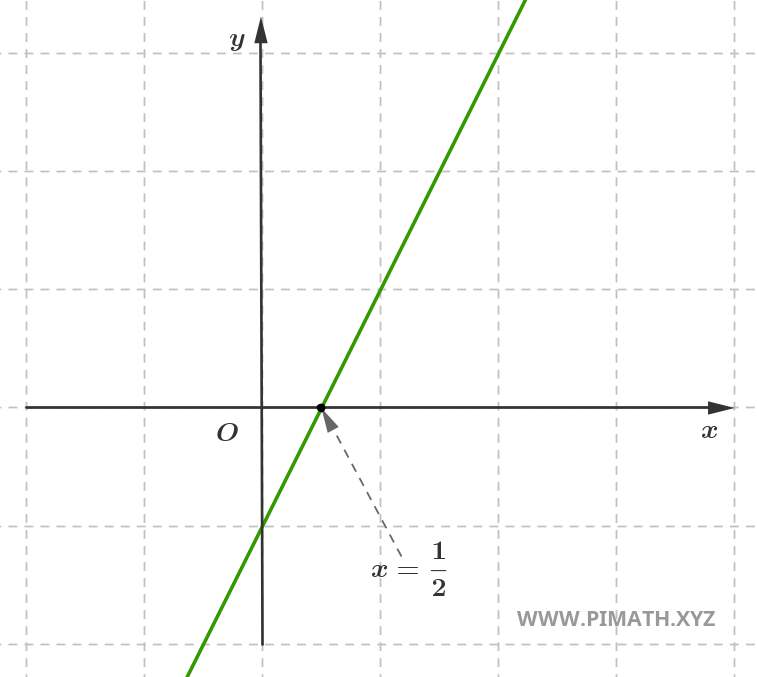
interseca l'asse delle ascisse (asse \( x \)). Ad esempio, la retta di equazione \( y = 2x - 1 \)
interseca l'asse delle ascisse nel punto \( x = \displaystyle \frac{1}{2} \), come mostrato in figura.
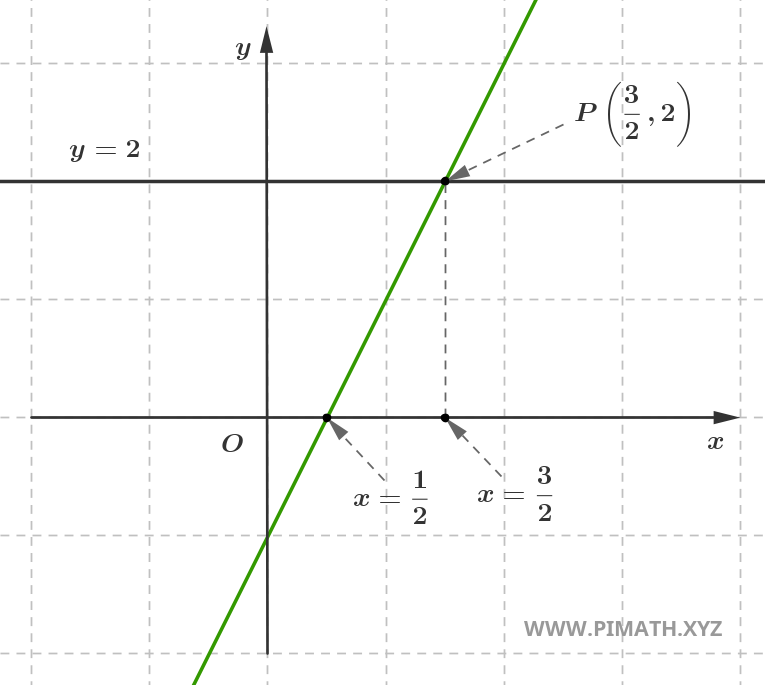
Abbiamo detto che la soluzione di una equazione di primo grado \( ax + b = 0 \) è l'ascissa in cui la retta interseca con l'asse \(x\). Ora, poniamoci un'altra domanda: come possiamo determinare il valore di \( x \) per il quale la retta \( y = ax + b \) assume un valore specifico, ad esempio \( y = 2 \)?
Per fare questo, basta imporre \( y = 2 \) nell’equazione della retta. Otteniamo così \( 2 = 2x - 1 \iff 2x - 3 = 0 \), dunque:
\[ x=\frac{3}{2} \]
Come mostrato in figura, alla soluzione che abbiamo trovato corrisponde l'ordinata \(y=2\).