Gli insiemi sono ovunque intorno a noi: l'insieme degli studenti della tua classe, l'insieme delle canzoni nella tua playlist preferita, l'insieme dei numeri pari. Ma cosa succede quando questi insiemi si "incontrano"? Come possiamo combinarli, confrontarli, separarli?
La risposta sta nelle operazioni tra insiemi: strumenti potenti che ci permettono di creare nuovi insiemi a partire da quelli esistenti. Queste operazioni seguono regole precise, creando un'algebra elegante che riflette la logica stessa del pensiero umano.
Indice
- Cosa Sono gli Insiemi
- L'Unione: Mettere Tutto Insieme
- L'Intersezione: Quello che Hanno in Comune
- La Differenza Insiemistica
- Il Complementare
- La Differenza Simmetrica
- Il Prodotto Cartesiano: Tutte le Combinazioni
- Le Leggi dell'Algebra degli Insiemi
- I Diagrammi di Venn: Visualizzare le Operazioni
Cosa Sono gli Insiemi
Prima di combinare gli insiemi, ricordiamo cosa sono. Un insieme è una collezione di oggetti distinti, chiamati elementi dell'insieme.
Esempi:
- \(A = \{1, 3, 5, 7, 9\}\) (i primi cinque numeri dispari positivi)
- \(B = \{2, 4, 6, 8, 10\}\) (i primi cinque numeri pari positivi)
- \(C = \{\text{rosso, verde, blu}\}\) (i colori primari)
- \(D = \{\text{lunedì, martedì, mercoledì}\}\) (i primi tre giorni della settimana)
Il concetto di appartenenza
Un elemento può appartenere a un insieme (\(\in\)) o non appartenere (\(\notin\)):
- \(3 \in A\) (\( 3 \) appartiene ad \( A \))
- \(4 \notin A\) (\( 4 \) non appartiene ad \( A \))
Ma ecco la domanda interessante: cosa succede quando vogliamo lavorare con più insiemi contemporaneamente? Come possiamo combinarli in modi diversi per ottenere nuove informazioni?
L'Unione: Mettere Tutto Insieme
Immagina di avere due playlist musicali e di voler creare una playlist che contenga tutte le canzoni di entrambe. Questa è l'idea dell'unione.
Definizione: L'unione di due insiemi \(A\) e \(B\), indicata con \(A \cup B\), è l'insieme di tutti gli elementi che appartengono ad \(A\) o a \(B\) (o a entrambi).
\[A \cup B = \{x : x \in A \text{ oppure } x \in B\}\]
Un esempio:
Prendiamo:
- \(A = \{1, 3, 5\}\) (numeri dispari fino a \( 5 \))
- \(B = \{2, 4, 5, 6\}\) (alcuni numeri pari e il \( 5 \))
Allora: \(A \cup B = \{1, 2, 3, 4, 5, 6\}\)
Nota importante: Il numero \( 5 \) appare in entrambi gli insiemi, ma nell'unione compare una sola volta. Gli insiemi non hanno elementi ripetuti!
Proprietà dell'unione
- Commutativa: \(A \cup B = B \cup A\) (l'ordine non importa)
- Associativa: \((A \cup B) \cup C = A \cup (B \cup C)\)
- Idempotente: \(A \cup A = A\) (unire un insieme con se stesso non cambia nulla)
- Elemento neutro: \(A \cup \emptyset = A\) (l'insieme vuoto non aggiunge nulla)
L'Intersezione: Quello che Hanno in Comune
A volte non vogliamo tutto, ma solo quello che è comune a più insiemi. Se due amici confrontano le loro playlist, potrebbero voler trovare le canzoni che piacciono a entrambi. Ecco l'intersezione.
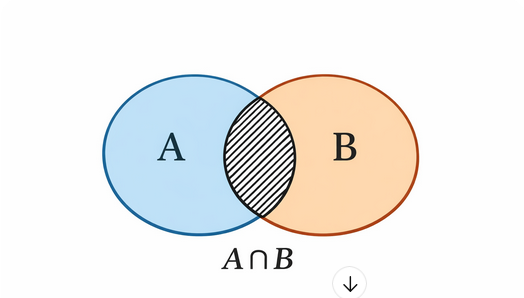
Definizione: L'intersezione di due insiemi \(A\) e \(B\), indicata con \(A \cap B\), è l'insieme di tutti gli elementi che appartengono sia ad \(A\) sia a \(B\).
\[A \cap B = \{x : x \in A \text{ e } x \in B\}\]
Un esempio:
Consideriamo:
- \(A = \{1, 2, 3, 4, 5\}\) (numeri da \( 1 \) a \( 5 \))
- \(B = \{3, 4, 5, 6, 7\}\) (numeri da \( 3 \) a \( 7 \))
Allora: \(A \cap B = \{3, 4, 5\}\) (gli elementi comuni)
Insiemi disgiunti
Cosa succede se due insiemi non hanno elementi in comune?
Esempio: \(C = \{1, 3, 5\}\) e \(D = \{2, 4, 6\}\)
Risultato: \(C \cap D = \emptyset\) (l'insieme vuoto)
Diciamo che \(C\) e \(D\) sono disgiunti.
Proprietà dell'intersezione
- Commutativa: \(A \cap B = B \cap A\)
- Associativa: \((A \cap B) \cap C = A \cap (B \cap C)\)
- Idempotente: \(A \cap A = A\)
- Elemento assorbente: \(A \cap \emptyset = \emptyset\)
La Differenza Insiemistica
A volte vogliamo sapere cosa c'è in un insieme ma non nell'altro. È come confrontare due liste della spesa per vedere cosa hai dimenticato di comprare.
Definizione: La differenza tra due insiemi \(A\) e \(B\), indicata con \(A \setminus B\) (o \(A - B\)), è l'insieme degli elementi che appartengono ad \(A\) ma non a \(B\).
\[A \setminus B = \{x : x \in A \text{ e } x \notin B\}\]
Un esempio:
Consideriamo:
- \(A = \{1, 2, 3, 4, 5\}\) (tutti i numeri da \( 1 \) a \( 5 \))
- \(B = \{3, 4\}\) (alcuni di questi numeri)
Allora:
- \(A \setminus B = \{1, 2, 5\}\) (quello che c'è in \(A\) ma non in \(B\))
- \(B \setminus A = \emptyset\) (tutto quello che c'è in \(B\) c'è anche in \(A\))
Attenzione: la differenza non è commutativa!
A differenza di unione e intersezione, l'ordine conta:
Se \(A = \{1, 2, 3\}\) e \(B = \{2, 3, 4\}\), allora:
- \(A \setminus B = \{1\}\)
- \(B \setminus A = \{4\}\)
Risultati completamente diversi!
Il Complementare
Spesso lavoriamo all'interno di un "universo" ben definito. Se stiamo parlando di studenti di una scuola, il nostro universo è l'insieme di tutti gli studenti. Il complementare di un insieme è tutto quello che non è in quell'insieme, ma è nel nostro universo.
Definizione: Dato un insieme universo \(U\) e un insieme \(A \subseteq U\), il complementare di \(A\) (indicato con \(A^c\)) è l'insieme di tutti gli elementi di \(U\) che non appartengono ad \(A\).
\[A^c = U \setminus A = \{x \in U : x \notin A\}\]
Un esempio:
Immaginiamo che:
- \(U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}\) (i numeri da 1 a 10)
- \(A = \{2, 4, 6, 8, 10\}\) (i numeri pari)
Allora: \(A^c = \{1, 3, 5, 7, 9\}\) (i numeri dispari)
Le Leggi di De Morgan
Il complementare gode delle proprietà scoperte dal matematico Augustus De Morgan:
- \((A \cup B)^c = A^c \cap B^c\)
- \((A \cap B)^c = A^c \cup B^c\)
In parole: "Il complementare dell'unione è l'intersezione dei complementari, e il complementare dell'intersezione è l'unione dei complementari." Queste leggi collegano le operazioni di unione e intersezione!
La Differenza Simmetrica
A volte vogliamo gli elementi che sono in un insieme o nell'altro, ma non in entrambi.
Definizione: La differenza simmetrica tra due insiemi \(A\) e \(B\), indicata con \(A \triangle B\), è l'insieme degli elementi che appartengono ad \(A\) o a \(B\), ma non a entrambi.
\[A \triangle B = (A \setminus B) \cup (B \setminus A) = (A \cup B) \setminus (A \cap B)\]
Un esempio:
Consideriamo due amici e i loro hobby:
- \(A = \{\text{calcio, tennis, nuoto}\}\) (hobby del primo amico)
- \(B = \{\text{tennis, basket, corsa}\}\) (hobby del secondo amico)
La differenza simmetrica \(A \triangle B = \{\text{calcio, nuoto, basket, corsa}\}\) rappresenta gli hobby che solo uno dei due pratica.
Proprietà interessanti
- Commutativa: \(A \triangle B = B \triangle A\)
- Associativa: \((A \triangle B) \triangle C = A \triangle (B \triangle C)\)
- Elemento neutro: \(A \triangle \emptyset = A\)
- Elemento inverso: \(A \triangle A = \emptyset\)
Queste proprietà rendono la differenza simmetrica particolarmente interessante in algebra!
Il Prodotto Cartesiano: Tutte le Combinazioni
Finora abbiamo combinato insiemi creando nuovi insiemi dello stesso "tipo". Il prodotto cartesiano è diverso: crea coppie di elementi.
Definizione: Il prodotto cartesiano di due insiemi \(A\) e \(B\), indicato con \(A \times B\), è l'insieme di tutte le coppie ordinate \((a, b)\) dove \(a \in A\) e \(b \in B\).
\[A \times B = \{(a, b) : a \in A \text{ e } b \in B\}\]
Un esempio:
Immagina di dover scegliere:
- \(A = \{\text{pasta, riso}\}\) (primi piatti)
- \(B = \{\text{pomodoro, pesto, carbonara}\}\) (condimenti)
Il prodotto cartesiano \(A \times B\) rappresenta tutte le possibili combinazioni:
\[A \times B = \{(\text{pasta, pomodoro}), (\text{pasta, pesto}), (\text{pasta, carbonara}),\] \[(\text{riso, pomodoro}), (\text{riso, pesto}), (\text{riso, carbonara})\}\]
Il piano cartesiano
Il prodotto cartesiano più famoso è \(\mathbb{R} \times \mathbb{R} = \mathbb{R}^2\), che rappresenta tutti i punti del piano cartesiano. Ogni punto \((x, y)\) è una coppia di numeri reali!
Proprietà del prodotto cartesiano
- Non commutativo: in generale \(A \times B \neq B \times A\)
- Distributivo rispetto all'unione: \(A \times (B \cup C) = (A \times B) \cup (A \times C)\)
- Cardinalità: \(|A \times B| = |A| \cdot |B|\)
Le Leggi dell'Algebra degli Insiemi
Le operazioni tra insiemi seguono regole precise, proprio come l'algebra dei numeri. Queste leggi ci permettono di semplificare espressioni complesse e di ragionare in modo rigoroso.
Leggi fondamentali
| Proprietà | Unione | Intersezione |
|---|---|---|
| Commutativa | \(A \cup B = B \cup A\) | \(A \cap B = B \cap A\) |
| Associativa | \((A \cup B) \cup C = A \cup (B \cup C)\) | \((A \cap B) \cap C = A \cap (B \cap C)\) |
| Distributiva | \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\) | \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\) |
| Idempotente | \(A \cup A = A\) | \(A \cap A = A\) |
| Elemento neutro | \(A \cup \emptyset = A\) | \(A \cap U = A\) |
| Elemento assorbente | \(A \cup U = U\) | \(A \cap \emptyset = \emptyset\) |
Le Leggi di De Morgan (ripassiamo)
- \((A \cup B)^c = A^c \cap B^c\)
- \((A \cap B)^c = A^c \cup B^c\)
Leggi di assorbimento
- \(A \cup (A \cap B) = A\)
- \(A \cap (A \cup B) = A\)
Queste leggi mostrano una bellissima simmetria: unione e intersezione sono operazioni "duali" - ogni proprietà di una si riflette nell'altra!
I Diagrammi di Venn: Visualizzare le Operazioni
A volte un'immagine vale più di mille equazioni. I diagrammi di Venn, inventati dal logico John Venn nel 1880, ci permettono di visualizzare le operazioni tra insiemi.
Come funzionano
Ogni insieme è rappresentato da un cerchio (o un'altra forma chiusa). L'insieme universo è rappresentato da un rettangolo che contiene tutto.
Le operazioni principali:
- Unione \(A \cup B\): tutta l'area coperta da almeno uno dei due cerchi
- Intersezione \(A \cap B\): l'area in cui i cerchi si sovrappongono
- Differenza \(A \setminus B\): la parte di \(A\) che non si sovrappone con \(B\)
- Complementare \(A^c\): tutto il rettangolo tranne il cerchio \(A\)
- Differenza simmetrica \(A \triangle B\): le parti che non si sovrappongono
Oltre i due insiemi
I diagrammi di Venn possono rappresentare anche tre o più insiemi, anche se diventano più complessi. Con tre insiemi ci sono \( 8 \) regioni distinte da considerare!
Vantaggi dei diagrammi di Venn
- Intuizione visiva: rendono le operazioni immediatamente comprensibili
- Verifica delle formule: permettono di controllare le leggi algebriche
- Risoluzione di problemi: aiutano a organizzare informazioni complesse
Le operazioni tra insiemi sono molto più di semplici manipolazioni simboliche. Sono il linguaggio matematico con cui descriviamo le relazioni tra gruppi, categorie e collezioni di oggetti. Ogni volta che raggruppiamo, confrontiamo, o combiniamo informazioni, stiamo usando questi strumenti.
La bellezza di queste operazioni sta nella loro universalità: le stesse regole che governano l'unione di due liste musicali governano anche l'intersezione di database aziendali o la classificazione di specie biologiche.
Ma c'è qualcosa di ancora più profondo. Le operazioni tra insiemi ci insegnano che la matematica non è solo calcolo - è un modo di organizzare il pensiero. Quando impariamo a vedere il mondo in termini di insiemi e delle loro relazioni, sviluppiamo una forma di ragionamento che è al tempo stesso rigorosa e flessibile.
Ogni operazione che abbiamo studiato rappresenta un diverso modo di mettere in relazione le idee:
- L'unione ci insegna l'inclusività: come mettere insieme diversità
- L'intersezione ci mostra l'importanza di ciò che è comune
- La differenza ci aiuta a identificare le specificità
- Il complementare ci ricorda che ogni scelta esclude delle alternative
E proprio come abbiamo visto con i numeri, anche qui ogni "impossibilità" ci spinge verso nuove scoperte. Quando gli insiemi semplici non bastano più, i matematici hanno inventato insiemi infiniti, insiemi di insiemi, e strutture ancora più elaborate.

