Lo studio delle posizioni reciproche tra due rette è uno degli argomenti fondamentali della geometria analitica piana. Comprendere come due rette possano posizionarsi nel piano cartesiano consente di classificare con precisione tutte le situazioni geometriche possibili: dall'intersezione a un unico punto fino alla sovrapposizione completa.
Indice
- Rappresentazione delle rette nel piano
- Classificazione delle posizioni reciproche
- Rette perpendicolari
- Esercizi svolti
Rappresentazione delle rette nel piano
Date due rette nel piano, possono presentarsi tre configurazioni principali:
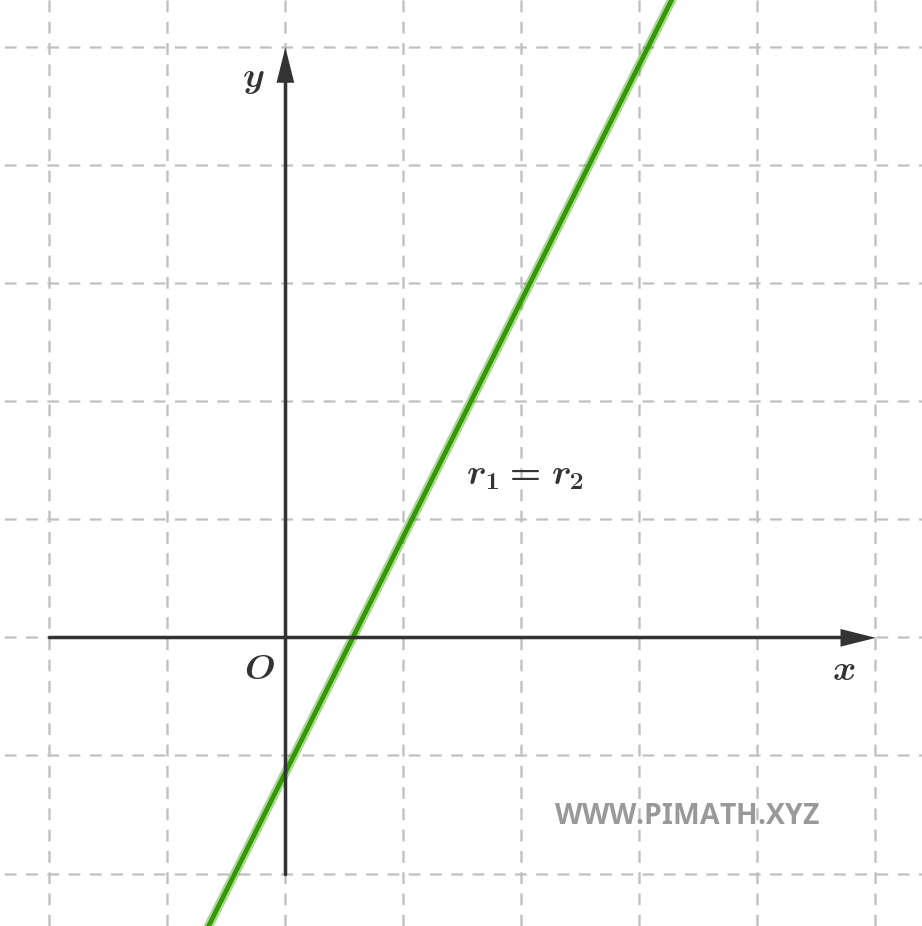
- Rette coincidenti: si tratta di due equazioni che descrivono in realtà la stessa retta. In questo caso, le rette hanno tutti i punti in comune e sono indistinguibili dal punto di vista geometrico.
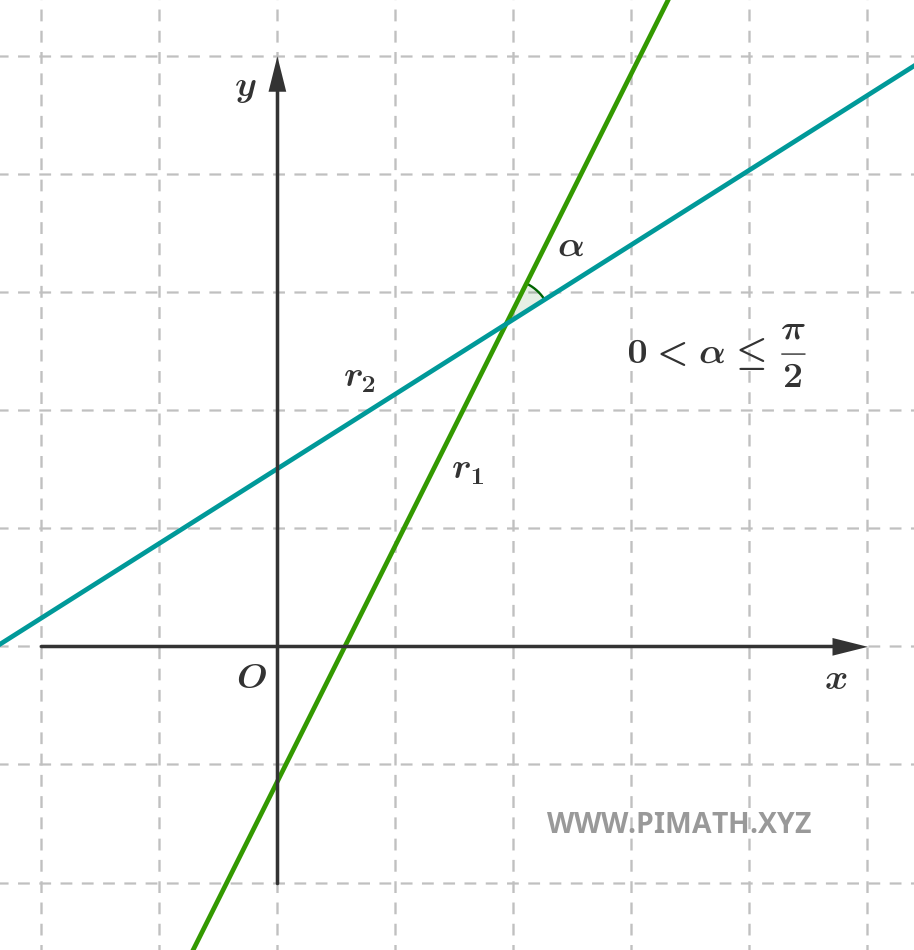
- Rette incidenti: si intersecano in un solo punto del piano, formando un angolo che può assumere qualsiasi ampiezza compresa tra 0° e 180°, esclusi i casi di parallelismo.
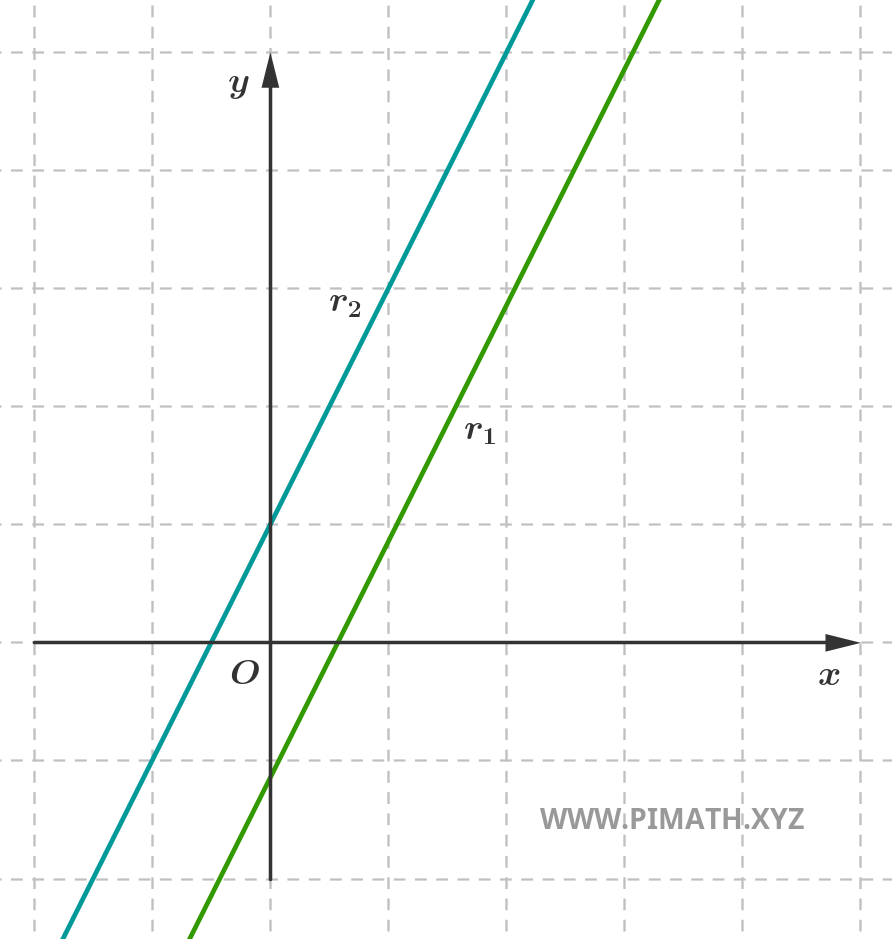
- Rette parallele distinte: pur avendo la stessa inclinazione (cioè lo stesso coefficiente angolare), queste rette non si incontrano mai. Non condividono alcun punto.
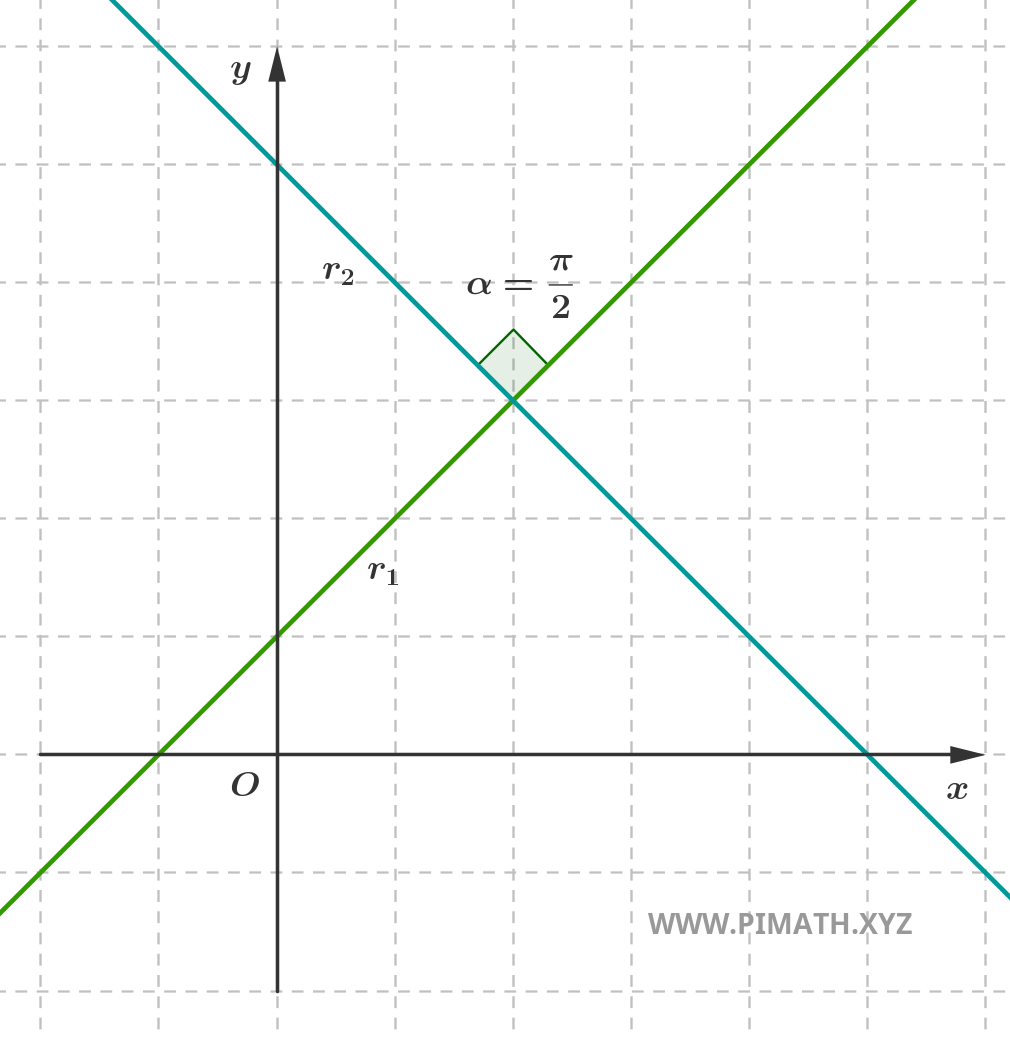
All'interno delle rette incidenti si colloca un caso particolare molto importante: quello delle rette perpendicolari. Due rette sono perpendicolari se si intersecano formando un angolo retto \( \displaystyle \frac{\pi}{2} \) (ossia di 90°).
Forme dell'equazione di una retta
Una retta nel piano cartesiano può essere rappresentata in più modi, equivalenti tra loro ma utili in contesti diversi.
La forma esplicita, anche detta forma ridotta, è forse la più intuitiva:
\[ y = mx + q \]
In questa equazione:
Il parametro \( m \in \mathbb{R} \) è detto coefficiente angolare e rappresenta la pendenza della retta. Per convenzione, se la retta è verticale, si dice che il coefficiente angolare è infinito o non è definito.
Il termine \( q \in \mathbb{R} \) è l'ordinata all'origine, cioè il punto in cui la retta interseca l'asse \( y \).
Un'altra modo di scrittura è la forma implicita, detta anche forma generale:
\[ ax + by + c = 0 \]
In questo caso, \( a, b, c \in \mathbb{R} \), e si deve avere \( a^2 + b^2 \neq 0 \) affinché si tratti effettivamente dell'equazione di una retta.
Relazione tra le forme
Quando il coefficiente \( b \) è diverso da zero, è possibile ricavare la forma esplicita a partire da quella implicita. Infatti, risolvendo rispetto a \( y \), si ottiene:
\[ ax + by + c = 0 \quad \Leftrightarrow \quad y = -\frac{a}{b}x - \frac{c}{b} \]
In tal modo, il coefficiente angolare risulta \( m = -\displaystyle \frac{a}{b} \) e l'ordinata all'origine è \( q = -\displaystyle \frac{c}{b} \).
Se invece \( b = 0 \) e \( a \neq 0 \), l'equazione si riduce alla forma \( x = -\displaystyle \frac{c}{a} \), che rappresenta una retta verticale. In questo caso, il coefficiente angolare non è definito.
Classificazione delle posizioni reciproche
Rette coincidenti
Due rette sono coincidenti quando coincidono punto per punto: ogni punto dell'una appartiene anche all'altra. In sostanza, si tratta della stessa retta espressa con due equazioni proporzionali.
Se sono espresse in forma esplicita, si ha:
\[ r: y = mx + q \quad \text{e} \quad s: y = mx + q \]
In forma implicita, due rette \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) sono coincidenti se e solo se esiste una costante \( k \neq 0 \) tale che:
\[ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} = k \]
Equivalentemente, ciò significa che \( (a_2, b_2, c_2) = k(a_1, b_1, c_1) \) per qualche \( k \neq 0 \).
Esempio: le rette \( 2x + 3y - 6 = 0 \) e \( 4x + 6y - 12 = 0 \) sono coincidenti, perché i coefficienti dell'una sono il doppio di quelli dell'altra:
\[ \frac{2}{4} = \frac{3}{6} = \frac{-6}{-12} = \frac{1}{2} \]
Rette parallele
Due rette sono parallele se hanno la stessa direzione. Nel caso in cui non coincidano, si dicono parallele distinte e non hanno punti in comune.
In forma esplicita, la condizione di parallelismo è:
\[ m_1 = m_2 \]
Se inoltre \( q_1 \neq q_2 \), allora le rette sono parallele distinte.
In forma implicita, due rette \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) sono parallele se e solo se:
\[ a_1b_2 - a_2b_1 = 0 \]
Questo equivale a dire che \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \) (quando \( a_2, b_2 \neq 0 \)).
Per avere parallelismo distinto, si deve inoltre verificare che:
\[ \frac{c_1}{c_2} \neq \frac{a_1}{a_2} \quad \text{(ovvero} \quad \frac{c_1}{c_2} \neq \frac{b_1}{b_2}\text{)} \]
Esempio: le rette \( r: y = 3x + 2 \) e \( s: y = 3x - 1 \) sono parallele distinte perché hanno lo stesso coefficiente angolare ma diversa ordinata all'origine.
Rette incidenti
Due rette sono incidenti se si intersecano in un unico punto. Questo accade quando le rette hanno direzioni diverse, cioè coefficienti angolari differenti (nel caso di rette non verticali).
In forma esplicita, basta verificare che:
\[ m_1 \neq m_2 \]
In forma implicita, la condizione è:
\[ a_1b_2 - a_2b_1 \neq 0 \]
Punto di intersezione
Per determinare il punto d'intersezione tra due rette incidenti espresse in forma implicita, si risolve il seguente sistema lineare:
\[ \begin{cases} a_1x + b_1y + c_1 = 0 \\ a_2x + b_2y + c_2 = 0 \end{cases} \]
Applicando la regola di Cramer, le coordinate del punto di intersezione sono:
\[ x = \frac{b_1c_2 - b_2c_1}{a_1b_2 - a_2b_1}, \quad y = \frac{a_2c_1 - a_1c_2}{a_1b_2 - a_2b_1} \]
purché \( a_1b_2 - a_2b_1 \neq 0 \).
Rette perpendicolari
Condizione di perpendicolarità
Due rette sono perpendicolari se si intersecano formando un angolo retto, cioè di 90°.
In forma esplicita, se le rette hanno coefficienti angolari \( m_1 \) e \( m_2 \) finiti, la condizione è:
\[ m_1 \cdot m_2 = -1 \]
Caso particolare: una retta orizzontale (\( m = 0 \)) è perpendicolare a una retta verticale (coefficiente angolare non definito).
In forma implicita, due rette \( r: a_1x + b_1y + c_1 = 0 \) e \( s: a_2x + b_2y + c_2 = 0 \) sono perpendicolari se e solo se:
\[ a_1a_2 + b_1b_2 = 0 \]
Questa relazione deriva dal fatto che i vettori normali delle due rette, \( \vec{n}_1 = (a_1, b_1) \) e \( \vec{n}_2 = (a_2, b_2) \), risultano ortogonali, cioè il loro prodotto scalare è nullo.
Dimostrazione analitica
L'angolo \( \theta \) tra due rette di coefficienti angolari \( m_1 \) e \( m_2 \) è espresso dalla formula:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1m_2} \right| \]
dove \( \theta \) rappresenta l'angolo acuto tra le due rette.
Se \( m_1m_2 = -1 \), il denominatore \( 1 + m_1m_2 \) si annulla e la tangente diventa indefinita, il che corrisponde a un angolo di 90°.
Esercizi svolti
Esercizio 1. Stabilire se le rette \( r: y = -2x + 1 \) e \( s: y = \displaystyle \frac{1}{2}x - 3 \) sono perpendicolari.
Determiniamo i coefficienti angolari:
\[ m_1 = -2 \]
\[ m_2 = \frac{1}{2} \]
Verifichiamo il prodotto tra i due coefficienti:
\[ m_1 \cdot m_2 = (-2) \cdot \frac{1}{2} = -1 \]
Poiché il prodotto è uguale a -1, possiamo concludere che le due rette sono perpendicolari.
Esercizio 2. Calcolare l'angolo acuto tra le rette \( r: y = 2x \) e \( s: y = -x \).
I coefficienti angolari sono:
\[ m_1 = 2 \]
\[ m_2 = -1 \]
Utilizziamo la formula per il calcolo dell'angolo acuto \( \theta \) tra due rette:
\[ \tan(\theta) = \left| \frac{m_2 - m_1}{1 + m_1 m_2} \right| = \left| \frac{-1 - 2}{1 + 2 \cdot (-1)} \right| = \left| \frac{-3}{1 - 2} \right| = \left| \frac{-3}{-1} \right| = 3 \]
Dunque:
\[ \theta = \arctan(3) \approx 71{,}57^\circ \]
Esercizio 3. Trovare l'equazione della retta perpendicolare a \( r: y = -\displaystyle \frac{3}{2}x + 4 \) e passante per il punto \( P(2, 1) \).
Il coefficiente angolare della retta data è \( m = -\displaystyle \frac{3}{2} \).
Il coefficiente angolare della retta perpendicolare sarà l'opposto del reciproco:
\[ m' = -\frac{1}{m} = -\frac{1}{-\frac{3}{2}} = \frac{2}{3} \]
Utilizziamo la formula del fascio proprio di rette passanti per \( P(2, 1) \):
\[ y - y_0 = m'(x - x_0) \quad \text{con } (x_0, y_0) = (2, 1) \] \[ y - 1 = \frac{2}{3}(x - 2) \] \[ y = \frac{2}{3}x - \frac{4}{3} + 1 = \frac{2}{3}x - \frac{1}{3} \]
L'equazione cercata è:
\[ y = \frac{2}{3}x - \frac{1}{3} \]
Esercizio 4. Determinare il valore di \( k \) affinché le rette \( r: 2x + 3y - 1 = 0 \) e \( s: kx + 6y + 2 = 0 \) siano parallele.
Due rette in forma implicita sono parallele se \( a_1b_2 - a_2b_1 = 0 \).
Identifichiamo i coefficienti:
- Retta \( r \): \( a_1 = 2, b_1 = 3, c_1 = -1 \)
- Retta \( s \): \( a_2 = k, b_2 = 6, c_2 = 2 \)
Applichiamo la condizione:
\[ a_1b_2 - a_2b_1 = 2 \cdot 6 - k \cdot 3 = 12 - 3k = 0 \] \[ 3k = 12 \quad \Rightarrow \quad k = 4 \]
Verifichiamo che per \( k = 4 \) le rette siano effettivamente parallele distinte:
\[ \frac{a_1}{a_2} = \frac{2}{4} = \frac{1}{2} \]
\[ \frac{b_1}{b_2} = \frac{3}{6} = \frac{1}{2} \]
\[ \frac{c_1}{c_2} = \frac{-1}{2} = -\frac{1}{2} \]
Poiché \( \displaystyle \frac{a_1}{a_2} = \displaystyle \frac{b_1}{b_2} \neq \displaystyle \frac{c_1}{c_2} \), le rette sono parallele distinte per \( k = 4 \).
Esercizio 5. Determinare il punto di intersezione tra le rette:
\( r: x + 2y - 3 = 0 \)
\( s: 2x - y + 1 = 0 \)
Risolviamo il sistema:
\[ \begin{cases} x + 2y = 3 \\ 2x - y = -1 \end{cases} \]
Utilizziamo il metodo di eliminazione. Moltiplichiamo la seconda equazione per 2:
\[ \begin{cases} x + 2y = 3 \\ 4x - 2y = -2 \end{cases} \]
Sommiamo le due equazioni:
\[ x + 4x + 2y - 2y = 3 + (-2) \] \[ 5x = 1 \quad \Rightarrow \quad x = \frac{1}{5} \]
Sostituiamo nella prima equazione:
\[ \frac{1}{5} + 2y = 3 \quad \Rightarrow \quad 2y = 3 - \frac{1}{5} = \frac{15 - 1}{5} = \frac{14}{5} \] \[ y = \frac{7}{5} \]
Il punto di intersezione è:
\[ \left( \frac{1}{5}, \frac{7}{5} \right) \]
Verifica: sostituendo in entrambe le equazioni originali si ottiene l'identità \( 0 = 0 \), confermando la correttezza del risultato.

