Desigualdades de Primeiro Grau

Uma desigualdade de primeiro grau é uma expressão algébrica que estabelece uma relação de ordem entre dois termos que contêm uma variável linear. Pode ser escrita na forma:

\[ a x + b \leq 0 \quad \text{ou} \quad a x + b \geq 0 \]

onde \( a \) e \( b \) são coeficientes reais com \( a \neq 0 \) e \( x \) é a variável desconhecida. Fala-se de desigualdade no sentido estrito quando

\[ a x + b < 0 \quad \text{ou} \quad a x + b > 0 \]

Índice

• Diferença entre Equações e Desigualdades de Primeiro Grau
• Princípios de Equivalência para Desigualdades
• Como Resolver Desigualdades de Primeiro Grau
• Representação Gráfica das Soluções das Desigualdades de Primeiro Grau

Uma equação de primeiro grau é uma igualdade entre duas expressões que contêm uma variável linear. Sua solução consiste em um único valor que satisfaz a igualdade. Já uma desigualdade de primeiro grau define um conjunto de valores para os quais a relação de ordem é verificada. O conjunto das soluções de uma desigualdade geralmente é composto por um intervalo de números reais.

A resolução de uma desigualdade de primeiro grau baseia-se em três princípios fundamentais:

Primeiro Princípio de Equivalência

O princípio de equivalência para as desigualdades, ou princípio de adição, afirma que, se adicionarmos ou subtrairmos o mesmo número a ambos os membros de uma desigualdade, a relação de ordem não muda. Por exemplo:

Se \( a x + b \leq 0 \), então podemos adicionar \( c \) a ambos os membros e obter:

\[ a x + b + c \leq c \]

Segundo Princípio de Equivalência

O segundo princípio de equivalência, afirma que, se multiplicarmos ou dividirmos ambos os membros de uma desigualdade por um número positivo, a relação de ordem não muda. No entanto, se multiplicarmos ou dividirmos por um número negativo, a desigualdade deve ser invertida. Aqui estão alguns exemplos:

Se \( a x + b \leq 0 \) e multiplicarmos ambos os membros por um número positivo \( k \), obtemos:

\[ k(a x + b) \leq k \cdot 0 \]

Se, por outro lado, multiplicarmos por um número negativo \( k \), a desigualdade se torna:

\[ k(a x + b) \geq k \cdot 0 \]

Atenção à Mudança de Sinal da Desigualdade

Quando multiplicamos ou dividimos ambos os membros de uma desigualdade por um número negativo, é fundamental inverter o sinal da desigualdade. Por exemplo:

Se \( -3 x \leq 6 \), dividindo ambos os membros por \( -3 \), devemos inverter o sinal da desigualdade:

\[ x \geq -2 \]

A resolução de uma inequação de primeiro grau pode ser dividida em passos claros e sistemáticos. Os passos gerais para resolver uma inequação de primeiro grau são:

Passos Gerais para Resolver uma Inequação

• Isolar o termo com a variável: Movemos todos os termos que não contêm a variável para um lado (geralmente o lado direito) da inequação e os termos que contêm a variável para o outro lado.
• Aplicar o princípio de adição ou subtração: Se necessário, somamos ou subtraímos o mesmo número de ambos os membros da inequação para isolar o termo com a variável.
• Multiplicar ou dividir por um coeficiente: Se a variável tem um coeficiente numérico, dividimos ambos os membros pelo coeficiente da variável. Se multiplicarmos ou dividirmos por um número negativo, lembramos de inverter o sinal da inequação.
• Verificação da solução: Uma vez isolada a variável, verificamos se a solução satisfaz a inequação inicial.

Exemplos Práticos com Explicações Passo a Passo

Vamos agora ver um exemplo prático de resolução de uma inequação de primeiro grau:

Exemplo 1. Resolva a inequação \( 3x - 5 \leq 7 \).

Começamos aplicando os passos descritos acima:

1. Isolar o termo com a variável: Somamos \( 5 \) a ambos os membros para obter: \[ 3x \leq 7 + 5 \quad \Rightarrow \quad 3x \leq 12 \]
2. Dividir ambos os membros por \( 3 \): Dividimos ambos os membros por \( 3 \) para isolar \( x \): \[ x \leq \frac{12}{3} \quad \Rightarrow \quad x \leq 4 \]
3. Verificação da solução: A solução \( x \leq 4 \) é a resposta final. Se substituirmos \( x = 4 \) na inequação original, teremos: \[ 3(4) - 5 = 12 - 5 = 7 \quad \Rightarrow \quad 7 \leq 7 \] O que é verdade. Portanto, a solução está correta e a representação gráfica é a seguinte:

Exemplo 2: Resolva a inequação \( -2x + 3 > 7 \)

Agora, vamos ver outro exemplo com um coeficiente negativo na frente da variável:

1. Isolar o termo com a variável: Primeiro subtraímos \( 3 \) de ambos os membros: \[ -2x > 7 - 3 \quad \Rightarrow \quad -2x > 4 \]
2. Dividir ambos os membros por \( -2 \): Quando dividimos por um número negativo, devemos inverter o sinal da inequação: \[ x < \frac{4}{-2} \quad \Rightarrow \quad x < -2 \]
3. Verificação da solução: A solução \( x < -2 \) está correta. Se substituirmos \( x = -3 \) (que é menor que -2), teremos: \[ -2(-3) + 3 = 6 + 3 = 9 \quad \Rightarrow \quad 9 > 7 \] O que é verdade. Portanto, a solução está correta e a representação gráfica é a seguinte.

Como já vimos, a representação gráfica das soluções de uma inequação do primeiro grau em uma reta numérica é uma maneira muito útil de visualizar o intervalo de soluções. Em geral, a solução de uma inequação do primeiro grau pode ser representada como um segmento ou parte da reta numérica, dependendo de a desigualdade ser aberta ou fechada.

Como Representar as Soluções em uma Reta Numérica

Para representar as soluções de uma inequação do primeiro grau em uma reta numérica, siga os seguintes passos:

1. Identificar a solução: Depois de resolver a inequação, determine o intervalo de soluções. Por exemplo, se a solução for \( x \leq 4 \), o intervalo de soluções será \( (-\infty, 4] \).
2. Traçar a reta numérica: Desenhe uma reta horizontal e marque os números significativos, como os limites do intervalo de soluções.
3. Indicar a solução:
   • Se a inequação for do tipo \( \leq \) ou \( \geq \), indique o limite do intervalo com um círculo fechado na reta numérica.
   • Se a inequação for do tipo \( < \) ou \( > \), indique o limite com um círculo aberto, o que significa que aquele ponto não está incluído na solução.
4. Indicar o intervalo: Trace uma linha contínua ou tracejada para representar o intervalo de soluções.

Interpretação Gráfica da Solução

A interpretação gráfica das soluções de uma inequação em uma reta numérica permite visualizar rapidamente qual é o conjunto de valores que satisfazem a relação. Aqui estão alguns exemplos de como as soluções são representadas:

Exemplo 1. Solução \( x \leq 4 \)

A solução \( x \leq 4 \) implica que todos os números menores ou iguais a \( 4 \) são soluções. A representação gráfica é a seguinte:

Solução. \( x \leq 4 \).

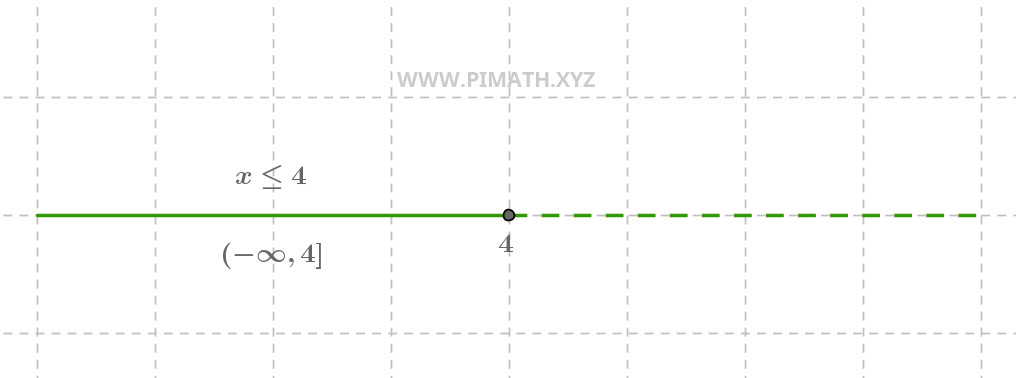
Na reta numérica, vemos um círculo fechado em \( 4 \) (porque \( 4 \) está incluído) e uma semi-reta que começa de \( -\infty \) e vai até \( 4 \).

Exemplo 2. Solução \( x > -2 \).

A solução \( x > -2 \) implica que todos os números maiores que \( -2 \) são soluções. A representação gráfica é a seguinte:

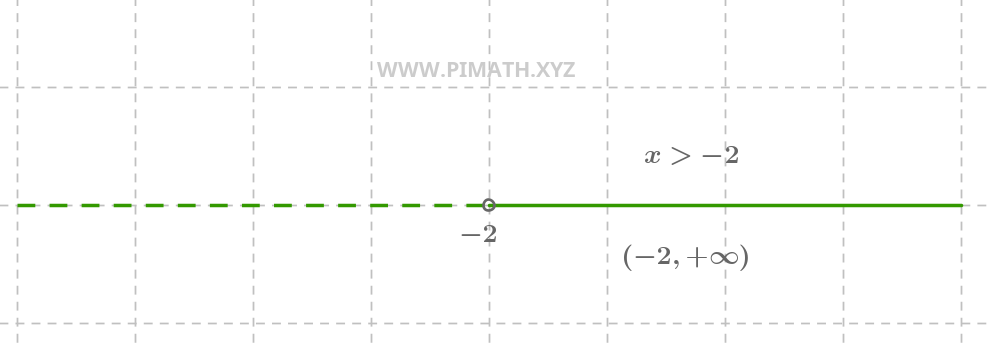
Na reta numérica, vemos um círculo aberto em \( -2 \) (porque \( -2 \) não está incluído) e uma linha contínua que começa de \( -2 \) e vai até \( +\infty \).

Exemplo 3. Solução \( -2 \leq x < 5 \)

A solução \( -2 \leq x < 5 \) é um intervalo que inclui \( -2 \) mas exclui \( 5 \). A representação gráfica é a seguinte:

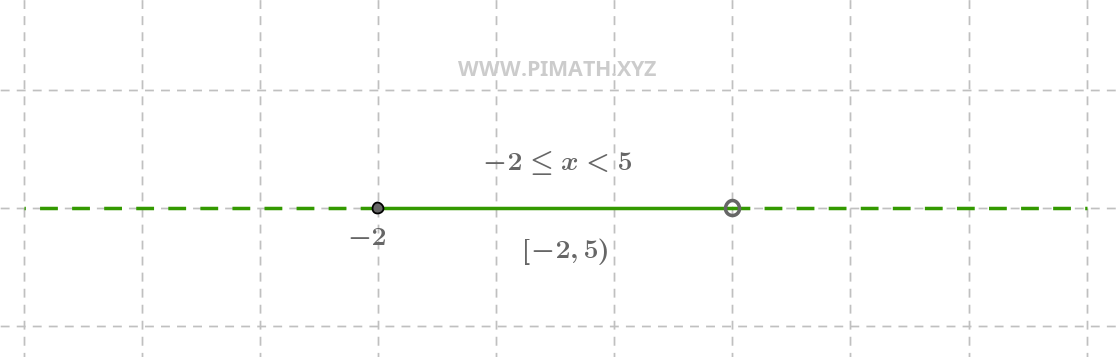
Na reta numérica, vemos um círculo fechado em \( -2 \) e um círculo aberto em \( 5 \), com uma linha contínua entre eles.

A interpretação gráfica dessas soluções mostra visualmente quais valores satisfazem a inequação, facilitando para quem estuda ver o conjunto de soluções.