A circunferência é o lugar geométrico dos pontos do plano que estão a uma distância constante de um ponto fixo, chamado centro. Esta distância constante denomina-se raio. A circunferência é uma curva fechada, simétrica em relação ao seu centro, e é um caso particular de cónica degenerada obtida seccionando um cone circular reto com um plano perpendicular ao eixo do cone.
Índice
- Definição Geométrica e Dedução da Equação
- Equação da Circunferência com Centro na Origem
- Equação da Circunferência com Centro Genérico
- Forma Geral e Completamento do Quadrado
- Condições para Representar uma Circunferência Real
- Posição de um Ponto em Relação à Circunferência
- Reta Tangente à Circunferência
- Interseção de Duas Circunferências
- Feixe de Circunferências
- Simetrias e Propriedades Geométricas
- Exercícios Resolvidos
Definição Geométrica e Dedução da Equação
Consideremos um ponto fixo \( C(x_0, y_0) \) no plano cartesiano ortogonal. A circunferência de centro \( C \) e raio \( r > 0 \) é o conjunto de pontos \( P(x, y) \) do plano tais que:
\[ d = \text{dist}(P, C) = r \]
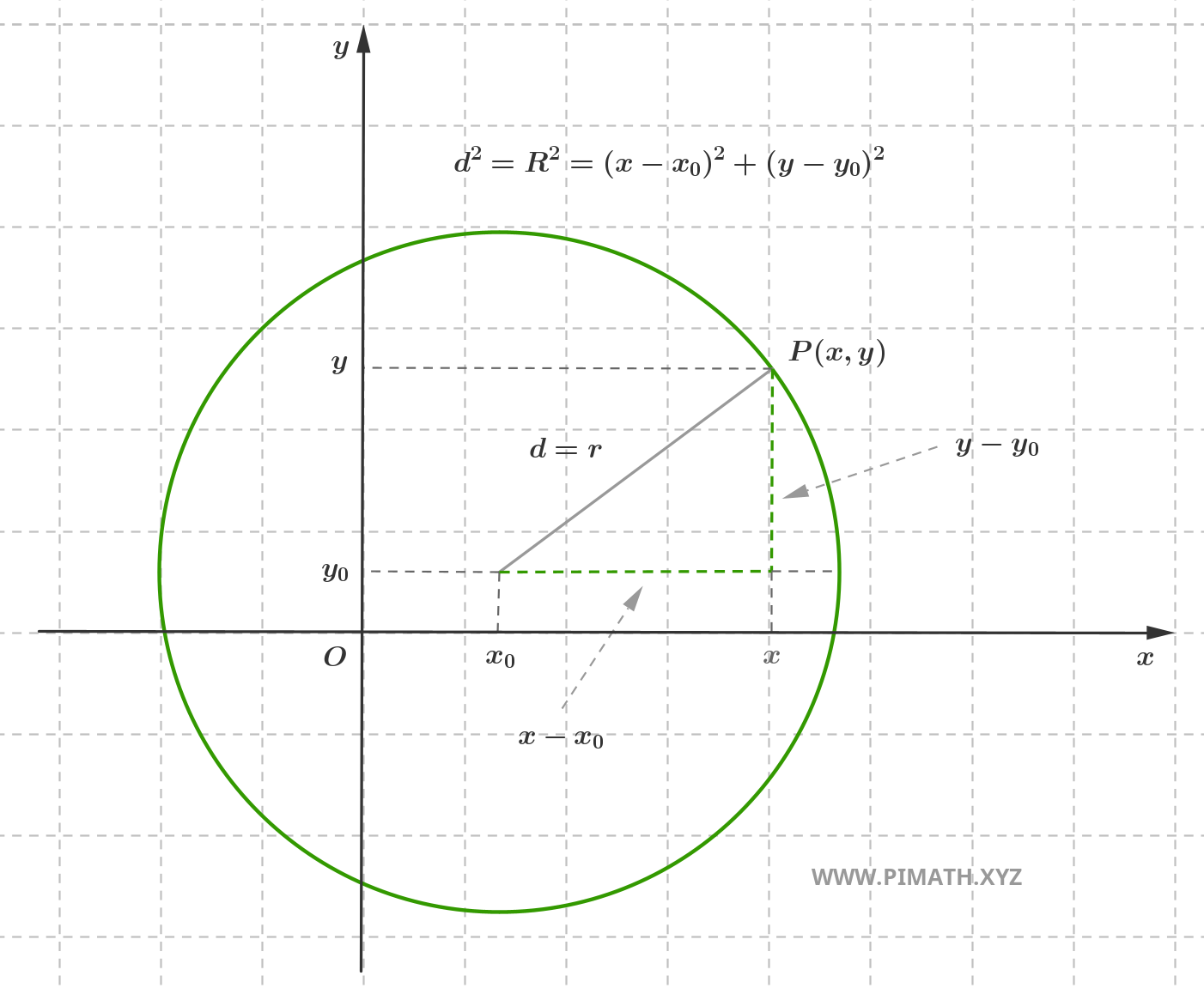
Aplicando a fórmula da distância euclidiana entre dois pontos no plano cartesiano, tem-se:
\[ \text{dist}(P, C) = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]
Impondo a condição \( \text{dist}(P, C) = r \), obtemos:
\[ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r \]
Elevando ao quadrado ambos os membros (operação lícita uma vez que ambos são não negativos, sendo \( r > 0 \) por definição):
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Esta é a forma canónica (ou forma normal) da equação da circunferência com centro \( C(x_0, y_0) \) e raio \( r \). A equação representa todos e apenas os pontos que satisfazem a condição geométrica de pertença à circunferência.
Equação da Circunferência com Centro na Origem
No caso particular em que o centro coincide com a origem do sistema de referência, isto é \( C(0, 0) \), pondo \( x_0 = 0 \) e \( y_0 = 0 \) na forma canónica, a equação simplifica-se notavelmente:
\[ x^2 + y^2 = r^2 \]
Esta é a equação mais elementar da circunferência e descreve o conjunto de todos os pontos equidistantes da origem dos eixos cartesianos. A equação goza das seguintes propriedades de simetria:
- Simetria em relação ao eixo das abscissas: se \( (x, y) \) pertence à circunferência, então também \( (x, -y) \) lhe pertence
- Simetria em relação ao eixo das ordenadas: se \( (x, y) \) pertence à circunferência, então também \( (-x, y) \) lhe pertence
- Simetria central em relação à origem: se \( (x, y) \) pertence à circunferência, então também \( (-x, -y) \) lhe pertence
Além disso, todos os diâmetros da circunferência passam pela origem e têm comprimento \( 2r \). O ponto \( (r, 0) \) representa a interseção da circunferência com o semieixo positivo das abscissas.
Equação da Circunferência com Centro Genérico
Consideremos agora o caso geral de uma circunferência com centro num ponto arbitrário \( C(x_0, y_0) \) do plano e raio \( r > 0 \). A equação canónica é:
\[ (x - x_0)^2 + (y - y_0)^2 = r^2 \]
Desenvolvendo os quadrados dos binómios utilizando as identidades algébricas \( (a \pm b)^2 = a^2 \pm 2ab + b^2 \), obtemos:
\[ x^2 - 2x \cdot x_0 + x_0^2 + y^2 - 2y \cdot y_0 + y_0^2 = r^2 \]
Reordenando os termos e passando todas as quantidades para o primeiro membro:
\[ x^2 + y^2 - 2x_0 x - 2y_0 y + (x_0^2 + y_0^2 - r^2) = 0 \]
Introduzimos agora os parâmetros:
\[ D = -2x_0 \quad , \quad E = -2y_0 \quad , \quad F = x_0^2 + y_0^2 - r^2 \]
Destas relações podemos obter:
\[ x_0 = -\frac{D}{2} \quad , \quad y_0 = -\frac{E}{2} \quad , \quad r^2 = x_0^2 + y_0^2 - F = \frac{D^2 + E^2}{4} - F \]
Substituindo na forma desenvolvida, obtemos a forma geral da equação da circunferência:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
Forma Geral e Completamento do Quadrado
Dada uma equação na forma geral:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
para a reconduzir à forma canónica e determinar centro e raio, utilizamos a técnica do completamento do quadrado. O método consiste em transformar as expressões \( x^2 + Dx \) e \( y^2 + Ey \) em quadrados perfeitos.
Para o termo em \( x \):
\[ x^2 + Dx = x^2 + Dx + \frac{D^2}{4} - \frac{D^2}{4} = \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} \]
Analogamente, para o termo em \( y \):
\[ y^2 + Ey = y^2 + Ey + \frac{E^2}{4} - \frac{E^2}{4} = \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} \]
Substituindo na equação geral:
\[ \left( x + \frac{D}{2} \right)^2 - \frac{D^2}{4} + \left( y + \frac{E}{2} \right)^2 - \frac{E^2}{4} + F = 0 \]
Reordenando:
\[ \left( x + \frac{D}{2} \right)^2 + \left( y + \frac{E}{2} \right)^2 = \frac{D^2 + E^2}{4} - F \]
Esta é a forma canónica, da qual podemos ler diretamente:
- Centro: \( C\left( -\displaystyle \frac{D}{2}, -\displaystyle\frac{E}{2} \right) \)
- Raio: \( r = \sqrt{\displaystyle\frac{D^2 + E^2}{4} - F} \) (desde que a expressão sob a raiz seja positiva)
Condições para Representar uma Circunferência Real
Uma equação da forma:
\[ ax^2 + by^2 + cxy + dx + ey + f = 0 \]
representa uma circunferência se e somente se são verificadas as seguintes condições:
- Coeficientes dos termos quadráticos iguais: \( a = b \neq 0 \)
- Ausência do termo misto: \( c = 0 \)
- Discriminante positivo: \( \Delta = \displaystyle \frac{d^2 + e^2}{4a^2} - \displaystyle \frac{f}{a} > 0 \)
No caso da forma padrão \( x^2 + y^2 + Dx + Ey + F = 0 \), a condição reduz-se a:
\[ \frac{D^2 + E^2}{4} - F > 0 \quad \Leftrightarrow \quad D^2 + E^2 - 4F > 0 \]
Distinguimos três casos:
- Se \( D^2 + E^2 - 4F > 0 \): a equação representa uma circunferência real com raio \( r = \displaystyle \frac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
- Se \( D^2 + E^2 - 4F = 0 \): a equação representa uma circunferência degenerada (um ponto)
- Se \( D^2 + E^2 - 4F < 0 \): a equação não tem soluções reais (circunferência imaginária)
Posição de um Ponto em Relação à Circunferência
Dada uma circunferência de equação \( (x - x_0)^2 + (y - y_0)^2 = r^2 \) e um ponto \( P(x_P, y_P) \), podemos determinar a posição relativa do ponto em relação à circunferência calculando a quantidade:
\[ \delta = (x_P - x_0)^2 + (y_P - y_0)^2 - r^2 \]
Temos três possibilidades:
- Se \( \delta = 0 \): o ponto pertence à circunferência
- Se \( \delta < 0 \): o ponto é interior à circunferência
- Se \( \delta > 0 \): o ponto é exterior à circunferência
Equivalentemente, comparando a distância \( d = \sqrt{(x_P - x_0)^2 + (y_P - y_0)^2} \) do ponto ao centro com o raio:
- Se \( d = r \): ponto sobre a circunferência
- Se \( d < r \): ponto interior
- Se \( d > r \): ponto exterior
Reta Tangente à Circunferência
Dada uma circunferência de centro \( C(x_0, y_0) \) e raio \( r \), e um ponto \( P(x_1, y_1) \) pertencente à circunferência, a equação da reta tangente à circunferência no ponto \( P \) é:
\[ (x_1 - x_0)(x - x_0) + (y_1 - y_0)(y - y_0) = r^2 \]
No caso particular de circunferência centrada na origem \( x^2 + y^2 = r^2 \), a equação da tangente no ponto \( P(x_1, y_1) \) simplifica-se em:
\[ x_1 x + y_1 y = r^2 \]
A reta tangente é perpendicular ao raio traçado no ponto de tangência. Este resultado deriva do facto de o vetor \( \overrightarrow{CP} = (x_1 - x_0, y_1 - y_0) \) ser normal à tangente.
Tangentes de um Ponto Exterior
De um ponto exterior \( P(x_P, y_P) \) a uma circunferência podem-se traçar exatamente duas retas tangentes. Os pontos de tangência obtêm-se resolvendo o sistema formado pela equação da circunferência e pela condição de que a distância do centro à reta seja igual ao raio.
Interseção de Duas Circunferências
Dadas duas circunferências:
\[ \Gamma_1: \quad x^2 + y^2 + D_1 x + E_1 y + F_1 = 0 \] \[ \Gamma_2: \quad x^2 + y^2 + D_2 x + E_2 y + F_2 = 0 \]
Para encontrar os pontos de interseção, resolvemos o sistema formado pelas duas equações. Subtraindo a segunda da primeira, obtemos a equação do eixo radical:
\[ (D_1 - D_2)x + (E_1 - E_2)y + (F_1 - F_2) = 0 \]
O eixo radical é uma reta que, quando as circunferências se intersectam, passa pelos dois pontos de interseção. As posições relativas das circunferências dependem da distância \( d \) entre os centros e dos raios \( r_1, r_2 \):
- Se \( d > r_1 + r_2 \): circunferências externas (nenhuma interseção)
- Se \( d = r_1 + r_2 \): circunferências tangentes externamente (um ponto de interseção)
- Se \( |r_1 - r_2| < d < r_1 + r_2 \): circunferências secantes (dois pontos de interseção)
- Se \( d = |r_1 - r_2| \): circunferências tangentes internamente (um ponto de interseção)
- Se \( d < |r_1 - r_2| \): uma circunferência interna à outra (nenhuma interseção)
Feixe de Circunferências
Um feixe de circunferências é um conjunto de circunferências dependentes de um parâmetro. O feixe gerado por duas circunferências \( \Gamma_1 \) e \( \Gamma_2 \) tem equação:
\[ \lambda \Gamma_1 + \mu \Gamma_2 = 0 \]
onde \( \lambda \) e \( \mu \) são parâmetros reais não ambos nulos. Explicitamente:
\[ \lambda(x^2 + y^2 + D_1 x + E_1 y + F_1) + \mu(x^2 + y^2 + D_2 x + E_2 y + F_2) = 0 \]
Distinguem-se diversos tipos de feixes:
- Feixe elíptico: as circunferências base não se intersectam; todas as circunferências do feixe são reais
- Feixe parabólico: as circunferências base são tangentes; o feixe contém retas (circunferências degeneradas)
- Feixe hiperbólico: as circunferências base intersectam-se em dois pontos; o feixe contém circunferências reais e imaginárias
Simetrias e Propriedades Geométricas
A circunferência possui notáveis propriedades de simetria que a tornam uma figura geométrica de particular interesse:
Simetrias
- Simetria central: toda a circunferência é simétrica em relação ao seu próprio centro
- Eixos de simetria: toda a reta que passa pelo centro é um eixo de simetria
- Invariância por rotação: a circunferência é invariante para qualquer rotação em torno do centro
Propriedades Métricas
- Comprimento (circunferência): \( C = 2\pi r \)
- Área do círculo: \( A = \pi r^2 \)
- Ângulo ao centro e inscrito: um ângulo inscrito é metade do correspondente ângulo ao centro
Exercícios Resolvidos
Exercício 1. Verificar se o ponto \( P(3, 4) \) pertence à circunferência de equação \( x^2 + y^2 = 25 \).
Solução. Substituímos as coordenadas do ponto na equação:
\[ 3^2 + 4^2 = 9 + 16 = 25 \]
Uma vez que a igualdade se verifica, o ponto \( P(3, 4) \) pertence à circunferência. Geometricamente, isto significa que a distância de \( P \) à origem é exatamente igual ao raio \( r = 5 \).
Exercício 2. Determinar a equação da circunferência com centro \( C(2, -3) \) e raio \( r = 4 \).
Solução. Aplicando a forma canónica:
\[ (x - 2)^2 + (y - (-3))^2 = 4^2 \] \[ (x - 2)^2 + (y + 3)^2 = 16 \]
Desenvolvendo, obtemos a forma geral:
\[ x^2 - 4x + 4 + y^2 + 6y + 9 = 16 \] \[ x^2 + y^2 - 4x + 6y - 3 = 0 \]
Exercício 3. Dada a equação \( x^2 + y^2 + 6x - 8y + 5 = 0 \), determinar centro e raio da circunferência.
Solução. Completamos os quadrados:
\[ x^2 + 6x = (x + 3)^2 - 9 \] \[ y^2 - 8y = (y - 4)^2 - 16 \]
Substituindo:
\[ (x + 3)^2 - 9 + (y - 4)^2 - 16 + 5 = 0 \] \[ (x + 3)^2 + (y - 4)^2 = 20 \]
Portanto:
- Centro: \( C(-3, 4) \)
- Raio: \( r = \sqrt{20} = 2\sqrt{5} \)
Exercício 4. Encontrar a equação da circunferência que passa pelos pontos \( A(1, 0) \), \( B(0, 1) \) e \( C(-1, 0) \).
Solução. Utilizamos a forma geral \( x^2 + y^2 + Dx + Ey + F = 0 \) e impomos a passagem pelos três pontos:
Para \( A(1, 0) \):
\[ 1 + 0 + D + 0 + F = 0 \implies D + F = -1 \]
Para \( B(0, 1) \):
\[ 0 + 1 + 0 + E + F = 0 \implies E + F = -1 \]
Para \( C(-1, 0) \):
\[ 1 + 0 - D + 0 + F = 0 \implies -D + F = -1 \]
Resolvendo o sistema:
\[ \begin{cases} D + F = -1 \\ E + F = -1 \\ -D + F = -1 \end{cases} \]
Da primeira e terceira equação: \( D = 0 \), portanto \( F = -1 \). Da segunda equação: \( E = 0 \).
A equação procurada é: \( x^2 + y^2 - 1 = 0 \), ou seja \( x^2 + y^2 = 1 \).
Esta é a circunferência unitária centrada na origem.
Exercício 5. Determinar as tangentes à circunferência \( x^2 + y^2 = 9 \) traçadas do ponto exterior \( P(5, 0) \).
Solução. Seja \( T(x_T, y_T) \) um ponto de tangência. A reta \( PT \) tem equação da tangente no ponto \( T \):
\[ x_T x + y_T y = 9 \]
Uma vez que esta reta passa por \( P(5, 0) \):
\[ 5x_T + 0 \cdot y_T = 9 \Rightarrow x_T = \frac{9}{5} \]
Sendo \( T \) sobre a circunferência: \( x_T^2 + y_T^2 = 9 \), portanto:
\[ \left(\frac{9}{5}\right)^2 + y_T^2 = 9 \Rightarrow y_T^2 = 9 - \frac{81}{25} = \frac{144}{25} \Rightarrow y_T = \pm\frac{12}{5} \]
Os pontos de tangência são:
\[ T_1\left(\frac{9}{5}, \frac{12}{5}\right) \quad \text{e} \quad T_2\left(\frac{9}{5}, -\frac{12}{5}\right) \]
As equações das tangentes são:
\[ \frac{9}{5}x + \frac{12}{5}y = 9 \quad \implies \quad 3x + 4y = 15 \] \[ \frac{9}{5}x - \frac{12}{5}y = 9 \quad \implies \quad 3x - 4y = 15 \]

