A elipse é o lugar geométrico dos pontos do plano para os quais a soma das distâncias a dois pontos fixos, chamados focos, é constante. Ela possui dois eixos de simetria, chamados eixo maior e eixo menor. É uma curva fechada e simétrica, com numerosas aplicações em física e geometria.
Índice
- Como encontrar a equação canônica da elipse
- Elipse com Semieixo Maior no Eixo das Ordenadas
- Como Encontrar a Equação da Elipse Transladada
- Relação entre os parâmetros da elipse
- Excentricidade da Elipse: Definição, Significado Geométrico e Fórmula
- Exercícios Resolvidos
Denotemos os dois focos como \( F_1(-c, 0) \) e \( F_2(c, 0) \), e seja \( P(x, y) \) qualquer ponto pertencente à elipse. Então vale a seguinte relação:
\[ |PF_1| + |PF_2| = 2a \]
A constante \( 2a \) – que representa a soma das distâncias \( |PF_1|\) e \(|PF_2|\) – é sempre maior que a distância entre os dois focos, \( 2c \). Este conceito é ilustrado na figura a seguir:
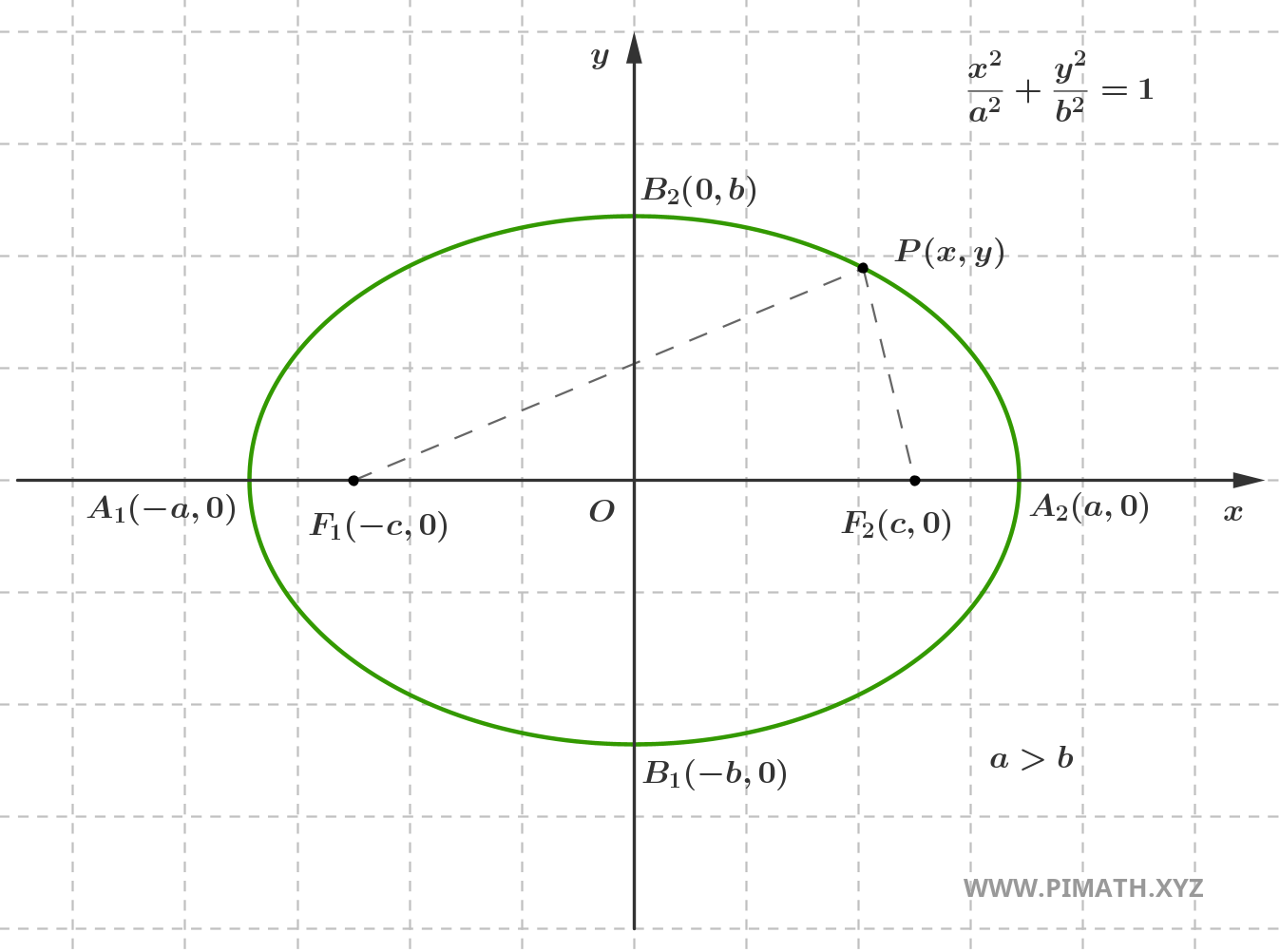
Na imagem, o segmento que liga o centro \( O \) ao ponto \( A_2 \) no eixo horizontal é chamado de semieixo maior, e seu comprimento é exatamente \( a \). O segmento vertical que liga o centro ao ponto \( B_2 \) é chamado de semieixo menor e tem comprimento \( b \).
A relação que define a elipse deve naturalmente valer para todos os pontos da elipse. Consideremos o caso particular em que o ponto \( P(x,y) \) coincide com o ponto \( B_2(0,b) \):
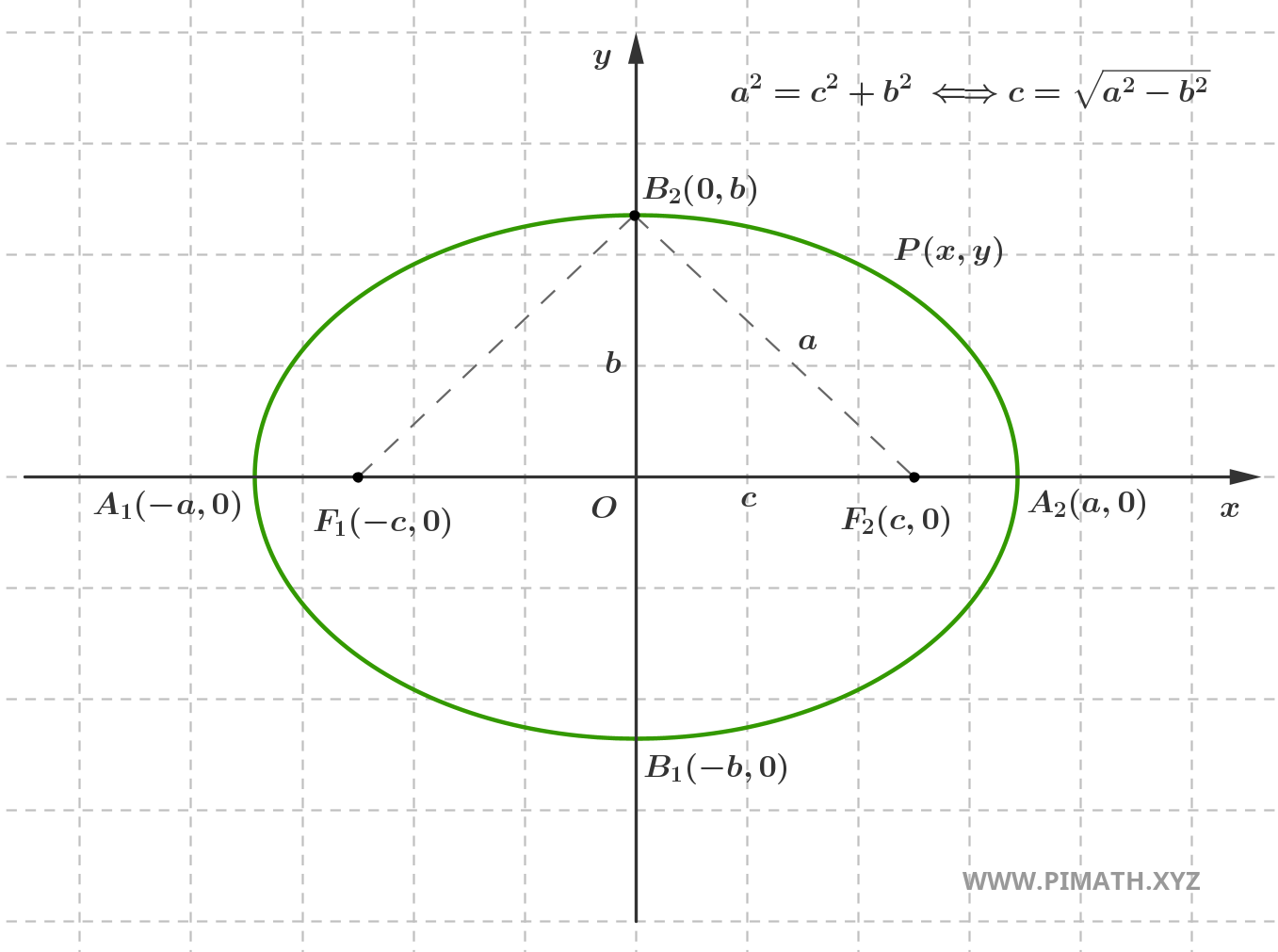
Considerando o triângulo retângulo com vértices \( O(0,0) \), \( F_2(c,0) \) e \( B_2(0,b) \) e aplicando o Teorema de Pitágoras, obtém-se que \( c=\sqrt{a^2-b^2} \), como mostrado na figura.
Como encontrar a equação canônica da elipse
Consideremos um caso simplificado no qual o centro da elipse coincide com a origem dos eixos cartesianos, com os focos posicionados ao longo do eixo horizontal nos pontos \( F_1(-c, 0) \) e \( F_2(c, 0) \).
Consideremos um ponto genérico \( P(x, y) \) no plano. Para que \( P \) pertença à elipse, deve valer a relação:
\[ |PF_1| + |PF_2| = 2a \quad , \quad a > c \]
Agora calculamos as distâncias entre o ponto \( P(x, y) \) e cada um dos dois focos:
\[ |PF_1| = \sqrt{(x + c)^2 + y^2} \quad \text{e} \quad |PF_2| = \sqrt{(x - c)^2 + y^2} \]
Substituindo essas expressões na condição inicial obtemos:
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a \]
Para eliminar um dos radicais, passamos \( \sqrt{(x + c)^2 + y^2} \) para o segundo membro:
\[ \sqrt{(x - c)^2 + y^2} = 2a - \sqrt{(x + c)^2 + y^2} \]
Elevamos ao quadrado ambos os membros para eliminar o radical:
\[ (x - c)^2 + y^2 = \left(2a - \sqrt{(x + c)^2 + y^2} \right)^2 \]
Desenvolvemos o quadrado do segundo membro:
\[ (x - c)^2 + y^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
Eliminamos o termo \( y^2 \) presente em ambos os lados e desenvolvemos os quadrados:
\[ x^2 - 2cx + c^2 = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} + x^2 + 2cx + c^2 \]
Simplificando ambos os membros:
\[ -4cx = 4a^2 - 4a\sqrt{(x + c)^2 + y^2} \]
Dividimos ambos os membros por 4:
\[ -cx = a^2 - a\sqrt{(x + c)^2 + y^2} \]
Passamos todos os termos com o radical para o primeiro membro:
\[ a\sqrt{(x + c)^2 + y^2} = a^2 + cx \]
Elevamos novamente ao quadrado ambos os membros:
\[ a^2[(x + c)^2 + y^2] = (a^2 + cx)^2 \]
Desenvolvemos ambos os lados:
\[ a^2(x^2 + 2cx + c^2 + y^2) = a^4 + 2a^2cx + c^2x^2 \]
Desenvolvemos completamente:
\[ a^2x^2 + 2a^2cx + a^2c^2 + a^2y^2 = a^4 + 2a^2cx + c^2x^2 \]
Simplificamos os termos comuns de ambos os lados:
\[ a^2x^2 - c^2x^2 + a^2y^2 = a^4 - a^2c^2 \]
Agrupamos os termos semelhantes:
\[ x^2(a^2 - c^2) + a^2y^2 = a^2(a^2 - c^2) \]
Visto que \( a > c \), a quantidade \( a^2 - c^2 \) é positiva. Vamos denotá-la como \( b^2 \), assim obtemos:
\[ b^2 = a^2 - c^2 \]
Substituindo, obtemos:
\[ x^2b^2 + a^2y^2 = a^2b^2 \]
Dividimos ambos os membros por \( a^2b^2 \) para isolar os termos:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , \quad a > b \]
Esta é a forma canônica da equação da elipse com centro na origem e focos no eixo das abscissas. A equação é simétrica em relação a ambos os eixos cartesianos e em relação à origem.
Introduzamos um pouco de nomenclatura. A reta que contém os focos é chamada de eixo focal, enquanto o ponto de interseção entre os eixos é o centro da elipse.
- Os pontos nos quais a elipse intersecta o eixo focal e a reta perpendicular a ele passando pelo centro são chamados de vértices da elipse.
- O segmento \( A_1A_2 \) é chamado de eixo maior, enquanto o segmento \( B_1B_2 \) é chamado de eixo menor.
- Define-se semieixo maior o comprimento \( a \), e semieixo menor o comprimento \( b \).
Elipse com Semieixo Maior no Eixo das Ordenadas
Se quisermos descrever uma elipse que tem o semieixo maior vertical, isto é, orientado ao longo do eixo das ordenadas, devemos simplesmente trocar os papéis de \( a \) e \( b \) na equação canônica que descreve a elipse com semieixo maior no eixo das abscissas, como mostrado na figura:
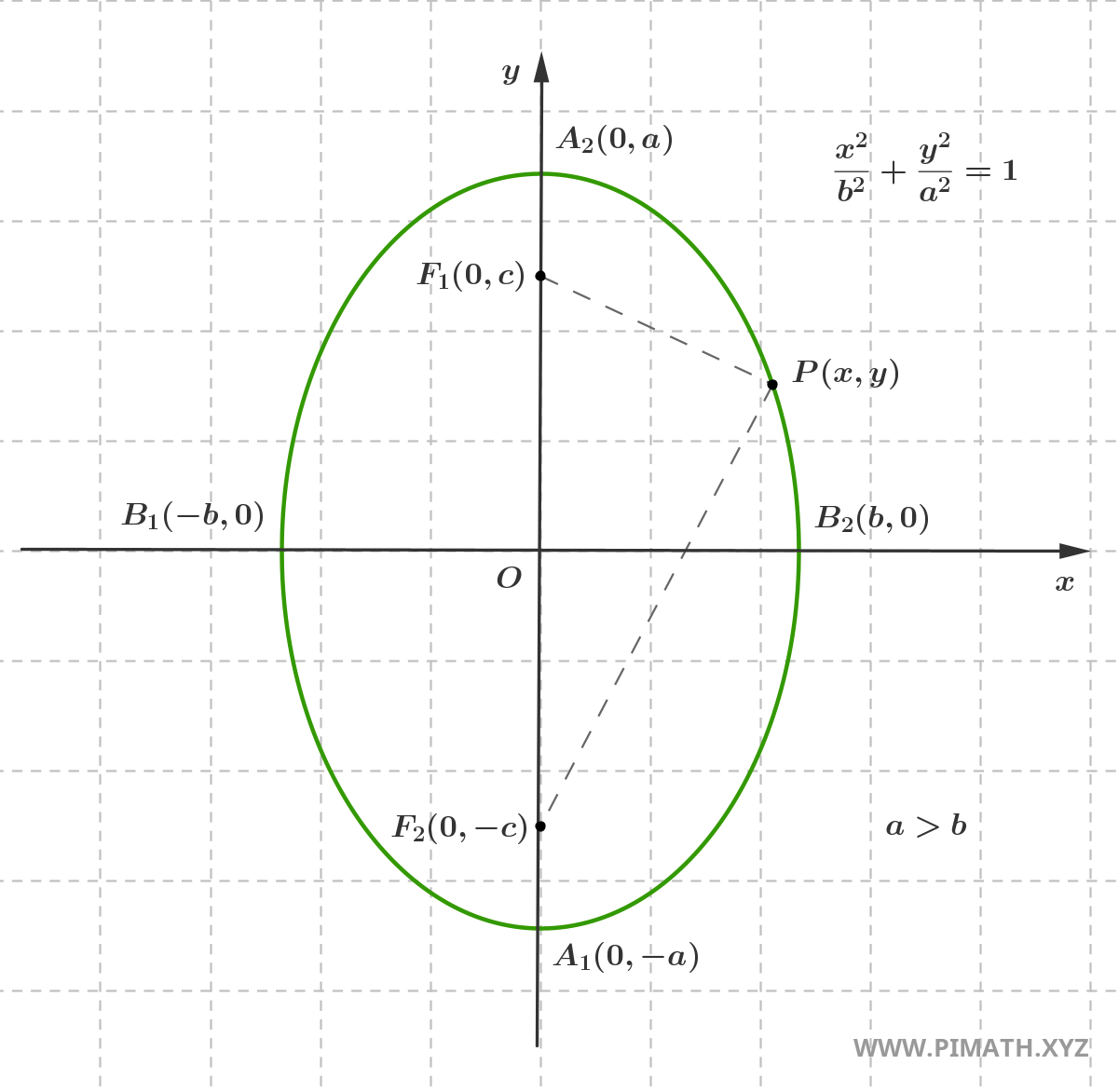
Neste caso, impondo \( |PF_1| + |PF_2| = 2a \) e com passos algébricos análogos, a equação da elipse torna-se:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \]
Esta mudança reflete uma rotação da elipse de 90 graus em relação ao eixo x. A forma da equação permanece a mesma, mas muda o eixo ao longo do qual a elipse se desenvolve.
Também neste caso o centro da elipse permanece na origem e a definição geométrica continua válida: para cada ponto \( P(x, y) \) na elipse, a soma das distâncias aos focos (que agora estão posicionados ao longo do eixo y) é sempre igual a \( 2a \).
Como Encontrar a Equação da Elipse Transladada
Até agora consideramos uma elipse com centro na origem e focos no eixo das abscissas. Entretanto, uma elipse pode estar localizada em qualquer ponto do plano. Neste caso, fala-se de elipse transladada.
Suponhamos que o centro da elipse esteja no ponto \( C(x_0, y_0) \). A equação canônica se modifica consequentemente, transladando as coordenadas.
Para a equação da elipse transladada, é fundamental distinguir qual é o semieixo maior e qual o semieixo menor. Dependendo da orientação da elipse em relação aos eixos cartesianos, a equação canônica transladada assume formas ligeiramente diferentes:
Elipse Transladada Horizontal
O eixo maior é paralelo ao eixo x, então os focos estão ao longo da reta \( y = y_0 \)
Neste caso, o semieixo maior \( a \) é o valor sob o termo \( (x - x_0)^2 \), e o semieixo menor \( b \) é o valor sob o termo \( (y - y_0)^2 \).
\[ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 \quad , \quad a > b \]
Elipse Transladada Vertical
O eixo maior é paralelo ao eixo y, então os focos estão ao longo da reta \( x = x_0 \)
Neste caso, o semieixo maior \( a \) é o valor sob o termo \( (y - y_0)^2 \), e o semieixo menor \( b \) é o valor sob o termo \( (x - x_0)^2 \).
\[ \frac{(x - x_0)^2}{b^2} + \frac{(y - y_0)^2}{a^2} = 1 \quad , \quad a > b \]
Nota: Os focos não se encontram mais nos eixos cartesianos x ou y, mas em retas paralelas a estes, passando pelo centro \( (x_0, y_0) \).
Relação entre os parâmetros da elipse
No caso de uma elipse com centro na origem e eixos paralelos aos eixos cartesianos, a relação entre os parâmetros principais é dada por uma fórmula fundamental que liga o semieixo maior \( a \), o semieixo menor \( b \) e a distância dos focos ao centro \( c \).
A fórmula é a seguinte:
\[ c^2 = a^2 - b^2 \]
Portanto, a distância dos focos ao centro pode ser calculada como:
\[ c = \sqrt{a^2 - b^2} \]
Esta relação é válida para todas as elipses com centro na origem e eixos alinhados aos eixos cartesianos, onde \( a > b \). O semieixo maior está sempre associado ao eixo com o denominador maior na equação canônica da elipse:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad , a > b \quad \text{(se o eixo maior é horizontal)} \]
Por outro lado:
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \quad , \quad a > b \quad \text{(se o eixo maior é vertical)} \]
Neste caso, \( c^2 = a^2 - b^2 \) e portanto \( c = \sqrt{a^2 - b^2} \). Conhecer essas relações permite calcular rapidamente a posição dos focos e compreender melhor a geometria da elipse.
Excentricidade da Elipse: Definição, Significado Geométrico e Fórmula
A excentricidade é uma medida fundamental que nos permite entender o quanto uma elipse se afasta de ser um círculo. Toda elipse tem dois focos: são dois pontos internos tais que a soma das distâncias de qualquer ponto da elipse aos dois focos é constante. A excentricidade, indicada pela letra \( e \), é um número que varia de \( 0 \) a \( 1 \) e descreve a forma da elipse.
Definição de Excentricidade
A excentricidade \( e \) não é um dado que se escolhe arbitrariamente, mas um valor que emerge naturalmente das propriedades geométricas da elipse. Em particular, se \( a \) é o comprimento do semieixo maior e \( b \) o do semieixo menor, então a distância \( c \) entre o centro e um dos focos é: \[c = \sqrt{a^2 - b^2}\] Com \( a > b \), a excentricidade é sempre dada pela seguinte fórmula: \[e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{1-\frac{b^2}{a^2}}\] Esta fórmula é válida tanto quando o eixo maior é horizontal quanto quando é vertical, pois \( a \) representa sempre o semieixo maior independentemente da orientação da elipse.
Significado Geométrico da Excentricidade
Quando a excentricidade é igual a zero, isto é \( e = 0 \), significa que os dois focos coincidem no centro da elipse. Neste caso a elipse é na realidade uma circunferência, porque todos os raios (isto é, os segmentos que unem o centro a um ponto da curva) têm o mesmo comprimento: \( a = b \).
Quando, ao contrário, a excentricidade é um número compreendido entre \( 0 \) e \( 1 \), isto é \( 0 < e < 1 \), a elipse é alongada. Quanto maior o valor de \( e \), mais os focos se afastam do centro e mais a elipse aparece alongada ao longo do eixo maior e comprimida ao longo do eixo menor.
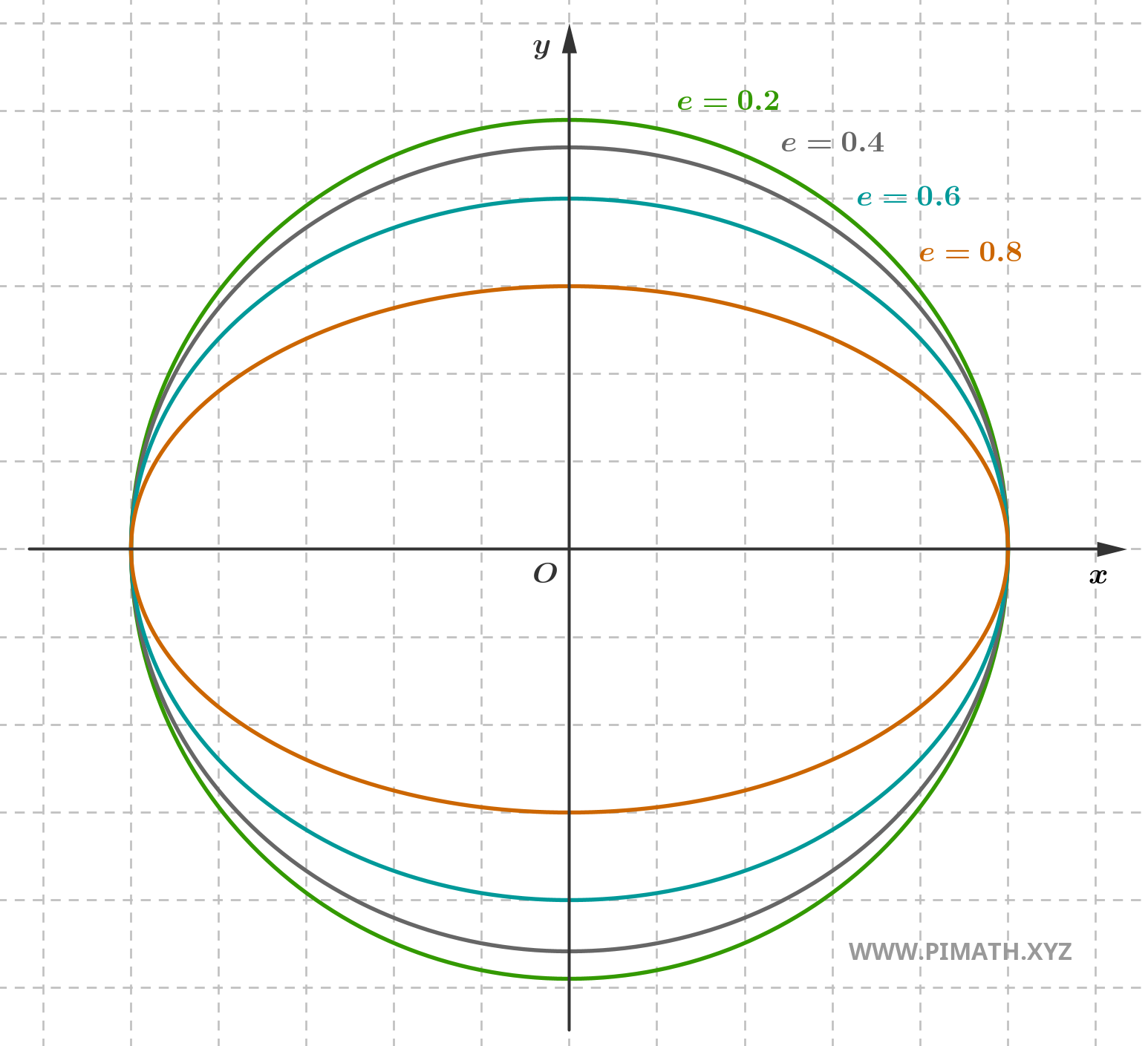
Finalmente, quando \( e \) se aproxima de \( 1 \), a forma da elipse torna-se extremamente alongada e os focos estão muito distantes do centro.
Por exemplo, consideremos uma elipse com semieixo maior \( a = 5 \) e semieixo menor \( b = 3 \).
Calculamos primeiro a distância dos focos ao centro:
\[c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4\]
Neste ponto podemos calcular a excentricidade:
\[e = \frac{4}{5} = 0{,}8\]
O valor que encontramos indica que a elipse está bastante achatada e os focos estão bem separados do centro. Aqui está o gráfico:
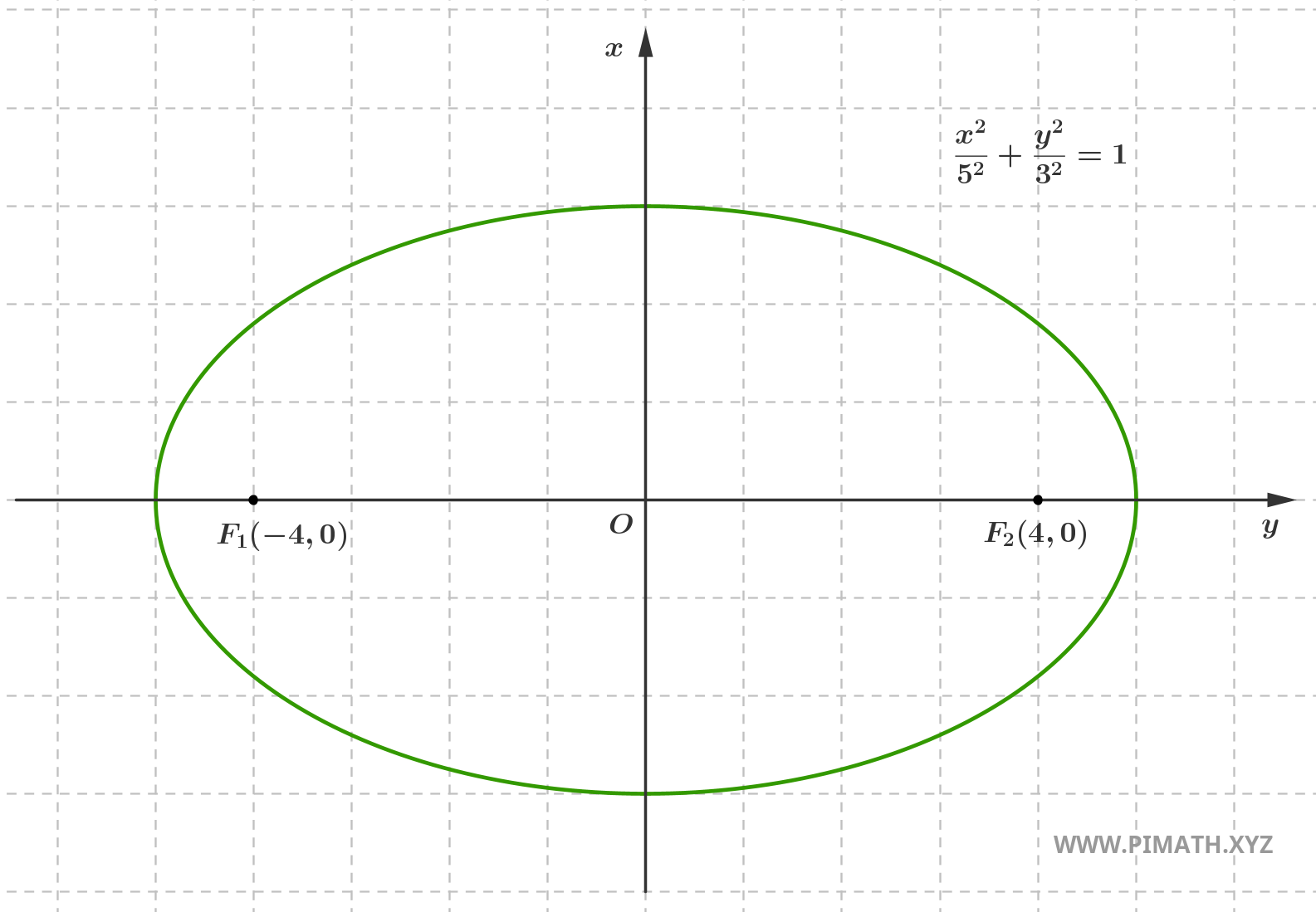
A excentricidade da elipse é um conceito que relaciona a posição dos focos com a forma geral da curva. Não é apenas uma fórmula para memorizar, mas uma ferramenta útil para intuir visualmente o quão próxima a elipse está de um círculo ou o quão alongada ela está. Lembre-se: quanto mais próximo \( e \) estiver de zero, mais a elipse se parece com um círculo. Quanto mais próximo \( e \) estiver de \( 1 \), mais achatada ela está e mais distantes estão os focos.
Exercícios Resolvidos
Exercício 1. Verificar se o ponto \( P(3, 2) \) pertence à elipse de equação:
\[ \frac{x^2}{9} + \frac{y^2}{4} = 1 \]
Solução. Substituímos \( x = 3 \), \( y = 2 \):
\[ \frac{3^2}{9} + \frac{2^2}{4} = \frac{9}{9} + \frac{4}{4} = 1 + 1 = 2 \neq 1 \]
Isto significa que o ponto não pertence à elipse.
Exercício 2. Uma elipse tem centro na origem, eixo maior horizontal, semieixo maior \( a = 5 \) e semieixo menor \( b = 3 \). Encontrar a equação da elipse.
Solução. A equação canônica é
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Rightarrow \frac{x^2}{25} + \frac{y^2}{9} = 1 \]
Exercício 3. Determine a posição dos focos da elipse de equação:
\[ \frac{x^2}{16} + \frac{y^2}{9} = 1 \]
Encontrar a distância dos focos \( c \).
Solução. Da equação \( \displaystyle \frac{x^2}{16} + \displaystyle \frac{y^2}{9} = 1 \), identificamos que o termo maior (16) está sob \( x^2 \), então o eixo maior é horizontal.
Segundo nossa convenção: \( a^2 = 16 \), \( b^2 = 9 \), portanto \( a = 4 \), \( b = 3 \).
Calculamos a distância dos focos \( c \) usando:
\[ c^2 = a^2 - b^2 = 16 - 9 = 7 \Rightarrow c = \sqrt{7} \]
Os focos se encontram nos pontos \( F_1(-\sqrt{7}, 0) \), \( F_2(\sqrt{7}, 0) \).
Exercício 4. Escreva a equação canônica da elipse com centro na origem, eixo maior vertical, sabendo que os vértices se encontram nos pontos \( (0, \pm 6) \) e os focos se encontram nos pontos \( (0, \pm 4) \).
Solução. Se os vértices estão em \( (0, \pm 6) \), então o semieixo maior é \( a = 6 \), portanto \( a^2 = 36 \).
Os focos estão em \( (0, \pm 4) \), portanto \( c = 4 \), portanto \( c^2 = 16 \).
Calculamos:
\[ b^2 = a^2 - c^2 = 36 - 16 = 20 \]
A equação da elipse, com eixo maior vertical, é: \[ \displaystyle \frac{x^2}{b^2} + \displaystyle \frac{y^2}{a^2} = 1 \Rightarrow \frac{x^2}{20} + \frac{y^2}{36} = 1 \]
Exercício 5. Uma elipse tem os focos nos pontos \( F_1(-3,0) \) e \( F_2(3,0) \), e passa pelo ponto \( P(4,1) \). Encontre a equação canônica da elipse.
Solução. Os focos são \( F_1(-3, 0) \), \( F_2(3, 0) \). Então \( c = 3 \), portanto \( c^2 = 9 \).
O ponto \( P(4, 1) \) pertence à elipse. Por definição: \[ |PF_1| + |PF_2| = 2a \] Calculamos: \[ |PF_1| = \sqrt{(4 - (-3))^2 + (1 - 0)^2} = \sqrt{7^2 + 1^2} = \sqrt{49 + 1} = \sqrt{50} = 5\sqrt{2} \] \[ |PF_2| = \sqrt{(4 - 3)^2 + (1 - 0)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2} \] \[ \Rightarrow |PF_1| + |PF_2| = 5\sqrt{2} + \sqrt{2} = 6\sqrt{2} \] \[ \Rightarrow 2a = 6\sqrt{2} \Rightarrow a = 3\sqrt{2} \Rightarrow a^2 = (3\sqrt{2})^2 = 9 \cdot 2 = 18 \] \[ b^2 = a^2 - c^2 = 18 - 9 = 9 \] A equação da elipse é portanto: \[ \frac{x^2}{18} + \frac{y^2}{9} = 1 \]

