Equação da reta

Sejam \( P_1(x_1,y_1) \) e \( P_2(x_2,y_2) \) dois pontos distintos no plano cartesiano. A reta que passa por esses dois pontos tem equação:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

que, multiplicando ambos os membros por \( y_2 - y_1 \), torna-se:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1). \]

• Semelhança de triângulos
• Interpretação geométrica
• Transformação na equação explícita
• Forma explícita da reta
• Inclinação da reta
• Interpretação da inclinação
• Forma implícita da reta
• Equação paramétrica da reta
• Reta perpendicular
• Exercícios

 Para demonstrar a equação da reta que passa por dois pontos, consideremos os pontos distintos \( P_1(x_1,y_1) \) e \( P_2(x_2,y_2) \) no plano cartesiano. Queremos mostrar que a equação:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

é satisfeita por qualquer ponto \( P(x,y) \) pertencente à reta.

Consideremos os triângulos na figura. Eles são semelhantes pelo critério do ângulo em comum (ângulo entre a reta e o eixo das abscissas) e pela proporcionalidade dos lados correspondentes:

\[ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \]

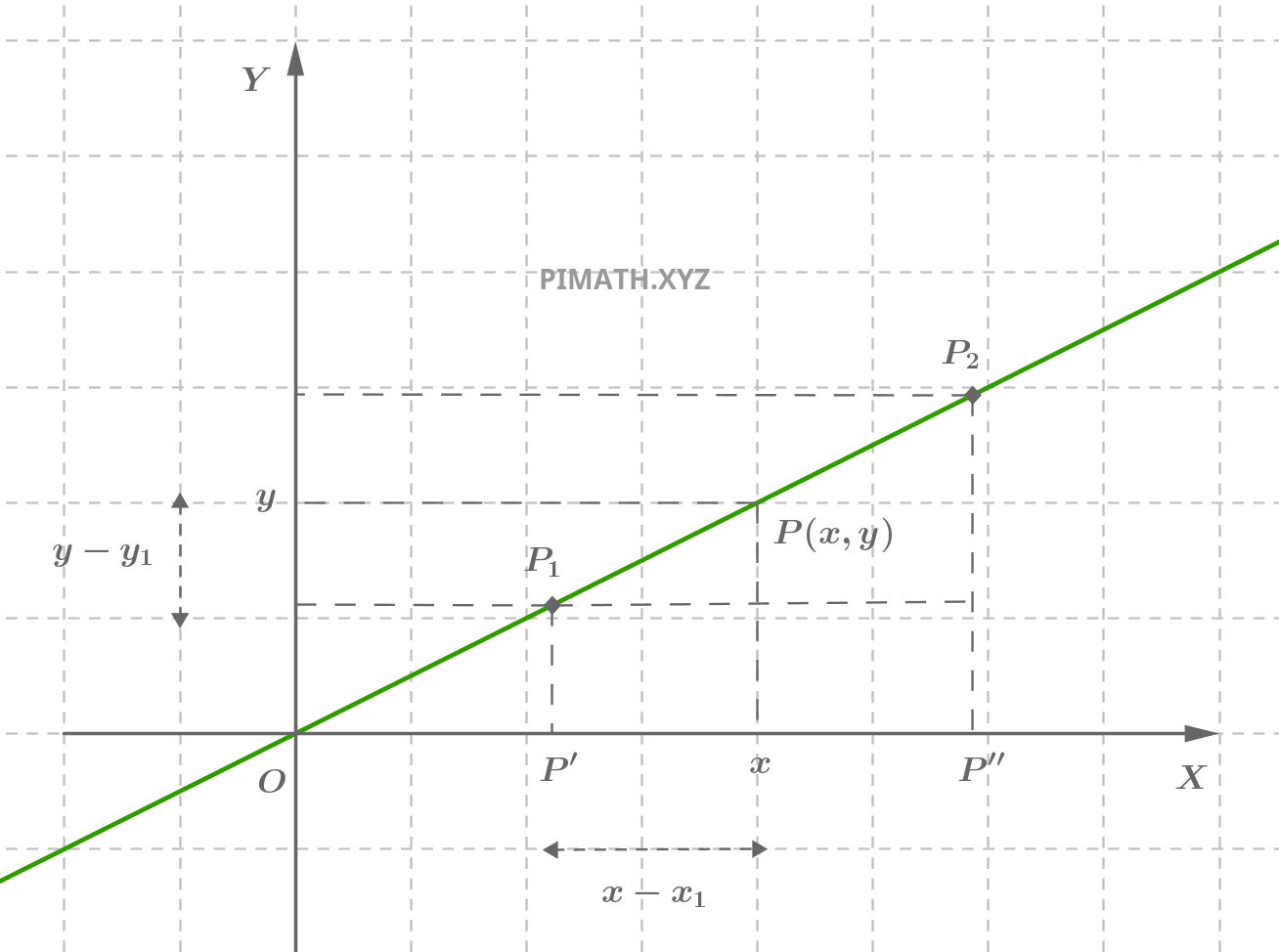
Essa relação segue diretamente da propriedade de semelhança de triângulos, garantindo que a razão entre as diferenças das ordenadas e das abscissas permanece constante ao longo da reta.

A fração \( \displaystyle \frac{y - y_1}{y_2 - y_1} \) representa a razão entre a altura do ponto genérico \( P \) em relação a \( P_1 \) e a altura total entre \( P_1 \) e \( P_2 \). Da mesma forma, \( \displaystyle \frac{x - x_1}{x_2 - x_1} \) mede a razão análoga para as abscissas. A igualdade entre essas duas razões indica que o ponto \( P \) está alinhado com \( P_1 \) e \( P_2 \), ou seja, pertence à reta que passa por esses dois pontos.

Multiplicando ambos os membros por \( y_2 - y_1 \), obtemos:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1), \]

que é a equação da reta na forma explícita \( y = mx + q \), com inclinação \( m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \).

Essa forma da equação é fundamental para descrever a relação linear entre \( x \) e \( y \) para todos os pontos da reta que passa por \( P_1 \) e \( P_2 \).

A equação da reta que passa por dois pontos distintos \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) pode ser expressa em forma explícita como segue:

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} \cdot (x - x_1) \]

Esta equação relaciona a variável \( y \) com a variável \( x \) ao longo da reta. Em outras palavras, para cada valor de \( x \) escolhido, a equação nos permite determinar o valor correspondente de \( y \), que é a coordenada do ponto na reta.

No contexto desta equação, o termo:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

representa a inclinação da reta, ou seja, o coeficiente angular. A inclinação é uma medida da inclinação da reta em relação ao eixo das abscissas (o eixo \( x \)). Se a inclinação for positiva, a reta é crescente (sobe da esquerda para a direita); se for negativa, a reta é decrescente (desce da esquerda para a direita).

Em outras palavras, a inclinação descreve a velocidade com que a reta cresce ou diminui em relação ao eixo horizontal \( x \). A inclinação é um parâmetro crucial para determinar a orientação da reta no plano cartesiano.

A inclinação \( m \) de uma reta que passa por dois pontos \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) é dada pela fórmula:

\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]

A inclinação mede a inclinação da reta em relação ao eixo das abscissas \( x \). Dependendo do valor da inclinação, podemos fazer as seguintes observações:

• Se \( m > 0 \), a reta é crescente, ou seja, sobe da esquerda para a direita. Isso significa que, para cada aumento em \( x \), \( y \) também aumenta. A reta forma um ângulo agudo com o eixo \( x \).
• Se \( m < 0 \), a reta é decrescente, ou seja, desce da esquerda para a direita. Neste caso, para cada aumento em \( x \), o valor de \( y \) diminui. A reta forma um ângulo obtuso com o eixo \( x \).
• Se \( x_2 = x_1 \), a inclinação é indefinida, o que implica que a reta é vertical. Nesse caso, não há variação horizontal (a diferença entre as abscissas \( x_2 - x_1 \) é zero), então não podemos definir uma inclinação numérica. A reta é paralela ao eixo \( y \) e não tem inclinação horizontal.

Em geral, a inclinação \( m \) nos dá informações importantes sobre o comportamento da reta. Se a reta é crescente, o valor de \( y \) aumenta à medida que \( x \) aumenta; se é decrescente, o valor de \( y \) diminui à medida que \( x \) aumenta; se a reta é vertical, significa que \( y \) não depende de \( x \) e a reta não tem nenhuma inclinação horizontal.

Partindo da forma explícita da equação da reta:

\[ y = y_1 + \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

podemos multiplicar ambos os membros por \( x_2 - x_1 \) para obter uma versão mais geral, e reescrever a equação da seguinte forma:

\[ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1} (x - x_1) \]

Multiplicando ambos os membros da equação por \( (x_2 - x_1) \), obtemos:

\[ (y - y_1)(x_2 - x_1) = (y_2 - y_1)(x - x_1). \]

Desenvolvendo os termos, obtemos:

\[ (x_2 - x_1) y - (x_2 - x_1) y_1 = (y_2 - y_1) x - (y_2 - y_1) x_1 \]

Agora, para obter uma forma implícita, queremos agrupar os termos de forma que a equação resulte em uma forma linear que não explicitamente mostre \( y \). Colocamos os termos que contêm \( y \) e \( x \) de um lado e os outros termos do outro lado:

\[ (y_2 - y_1) x - (x_2 - x_1) y = (y_2 - y_1) x_1 - (x_2 - x_1) y_1 \]

Escrevemos esta equação na forma implícita padrão:

\[ (y_2 - y_1) x - (x_2 - x_1) y + ((x_2 - x_1) y_1 - (y_2 - y_1) x_1) = 0. \]

Esta é a forma implícita da equação da reta. Se definirmos os coeficientes como \( a = y_2 - y_1 \), \( b = -(x_2 - x_1) \), e \( c = (x_2 - x_1) y_1 - (y_2 - y_1) x_1 \), a equação assume a forma geral:

\[ ax + by + c = 0 \]

Alternativamente, se introduzirmos a inclinação \( m = \frac{y_2 - y_1}{x_2 - x_1} \) e reorganizarmos os termos na equação anterior, podemos escrever:

\[ m(x_2 - x_1)x - (x_2 - x_1)y + ((x_2 - x_1)y_1 - m(x_2 - x_1)x_1) = 0 \]

Simplificando e dividindo por \( (x_2 - x_1) \), obtemos:

\[ mx - y + (y_1 - mx_1) = 0 \]

Nesta forma, os coeficientes são \( a = m \), \( b = -1 \), e \( c = y_1 - mx_1 \).

A forma implícita \( ax + by + c = 0 \) é uma representação mais geral de uma reta no plano cartesiano. Este formato é útil principalmente para aplicações geométricas e algébricas, onde o valor explícito de \( y \) não é necessário ou quando se deseja trabalhar diretamente com as propriedades algébricas da reta.

A reta que passa pelos pontos \( P_1(x_1, y_1) \) e \( P_2(x_2, y_2) \) também pode ser descrita de forma paramétrica. Nessa representação, as coordenadas \( x \) e \( y \) de um ponto na reta são expressas em função de um parâmetro real \( t \), que varia ao longo da reta.

A equação paramétrica da reta é dada por:

\[ \begin{cases} x = x_1 + (x_2 - x_1)t \\ y = y_1 + (y_2 - y_1)t \end{cases} \]

Aqui, \( t \) é o parâmetro que pode assumir qualquer valor real. Quando \( t \) varia, o ponto \( (x, y) \) se move ao longo da reta que conecta os dois pontos \( P_1 \) e \( P_2 \).

A forma paramétrica representa, portanto, uma família de pontos na reta, onde o parâmetro \( t \) define de maneira única cada ponto da reta. Quando \( t = 0 \), obtemos o ponto \( P_1(x_1, y_1) \); quando \( t = 1 \), obtemos o ponto \( P_2(x_2, y_2) \). Os valores de \( t \) entre 0 e 1 descrevem os pontos da reta entre \( P_1 \) e \( P_2 \), enquanto os valores de \( t \) superiores a 1 ou inferiores a 0 estendem a reta além desses pontos.

A fórmula paramétrica é baseada no conceito de vetor diretor, que é o vetor que conecta \( P_1 \) e \( P_2 \). De fato, a diferença \( (x_2 - x_1, y_2 - y_1) \) é o vetor diretor da reta, e o parâmetro \( t \) é o fator de escala que permite deslocar-se ao longo da reta.

Em forma vetorial, a equação paramétrica pode ser escrita como:

\[ \vec{r}(t) = \vec{P_1} + t \cdot (\vec{P_2} - \vec{P_1}) \]

onde \( \vec{r}(t) \) representa a posição de um ponto genérico na reta no tempo \( t \), e \( \vec{P_1} \) e \( \vec{P_2} \) são os vetores posição dos pontos \( P_1 \) e \( P_2 \), respectivamente.

A forma paramétrica é particularmente útil em vários campos da geometria analítica, como no estudo das curvas, em aplicações de gráficos computadorizados, ou em física para descrever o movimento de um objeto ao longo de uma trajetória reta.

Quando duas retas são perpendiculares, a sua inclinação está relacionada por uma relação bem definida. Se uma reta tem inclinação \( m \), a inclinação da reta perpendicular a ela é dada por:

\[ m_\perp = -\frac{1}{m}. \]

Esta fórmula expressa o fato de que o produto das inclinações de duas retas perpendiculares é igual a \(-1\). A razão dessa relação pode ser vista no fato de que os ângulos formados pelas duas retas devem ser de 90° (um ângulo reto), e, portanto, a tangente do ângulo entre as retas deve satisfazer essa condição.

Para encontrar a equação da reta perpendicular que passa por um ponto \( (x_1, y_1) \), podemos usar a forma ponto-inclinação. A inclinação da reta perpendicular é \( -\displaystyle \frac{1}{m} \), então a equação da reta perpendicular será:

\[ y - y_1 = -\frac{1}{m} (x - x_1) \]

Nessa equação, \( (x_1, y_1) \) é o ponto através do qual passa a reta perpendicular, enquanto \( m \) é a inclinação da reta original. A fórmula descreve uma reta que tem a inclinação oposta e inversa em relação à reta original.

Se a reta original for representada pela equação \( y = mx + q \), a reta perpendicular terá a inclinação \( m_\perp = -\displaystyle \frac{1}{m} \) e será escrita na forma \( y - y_1 = -\displaystyle \frac{1}{m} (x - x_1) \), onde \( (x_1, y_1) \) é o ponto de interseção entre a reta original e a reta perpendicular.

Essa propriedade das retas perpendiculares é fundamental em muitos campos da geometria, trigonometria e física, especialmente quando se estudam ângulos e trajetórias perpendiculares entre si.

Exercício 1: Determine a equação da reta que passa por \( A(1, 2) \) e \( B(3, 6) \).

Solução:

1. Calculamos a inclinação da reta: \[ m = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 \]
2. Utilizamos a equação ponto-inclinação para determinar a equação da reta que passa por \( A(1, 2) \) e tem inclinação \( m = 2 \): \[ y - 2 = 2(x - 1). \]
3. Desenvolvendo a equação: \[ y - 2 = 2x - 2. \]
4. Simplificando: \[ y = 2x - 2 + 2 = 2x. \]

Portanto, a equação da reta que passa pelos pontos \( A(1, 2) \) e \( B(3, 6) \) é \[ y = 2x. \]

Verificação: Podemos verificar que ambos os pontos satisfazem esta equação:

• Para \( A(1, 2) \): \[ 2 = 2 \cdot 1 = 2 \]
• Para \( B(3, 6) \): \[ 6 = 2 \cdot 3 = 6 \]

Exercício 2: Escreva a equação paramétrica da reta que passa por \( A(1, 2) \) e \( B(3, 6) \).

Solução:

1. Calculamos o vetor diretor \( \boldsymbol{v} = (x_2 - x_1, y_2 - y_1) \), que representa a direção da reta: \[ \boldsymbol{v} = (3 - 1, 6 - 2) = (2, 4). \]
2. As equações paramétricas da reta são: \[ \begin{cases} x = 1 + 2t \\ y = 2 + 4t \end{cases} \quad \text{com} \quad t \in \mathbb{R}. \]